1. Introduction
There is increasing interest in accurate monitoring and simulation of the surface temperature over the Antarctic plateau. Initial interest comes from the fact that snow surface temperature strongly controls the temperature of snow and firn layers at depths of tens (or hundreds) of meters beneath the surface. Hence, snow surface temperature strongly influences the thermal state of the whole East Antarctic ice sheet and its dynamics, shape, calving rate and, consequently, its mass balance. Reference Town, Waddington, Walden and WarrenTown and others (2008) have shown how a finite-volume snow model, using the observed snow surface temperature as input data, can efficiently reproduce the temperatures, heating rates and vapor pressures in near-surface snow at the South Pole during a 9 year simulation.
Further interest comes from the critical role that snow surface temperature plays on the energy balance of the Antarctic plateau. On one hand, the surface temperature directly affects a significant part of the surface energy budget, mainly by emission of longwave radiation but also through the latent and sensible heat fluxes, which are exchanged with the atmosphere and through heat diffusion towards deep snow and ice layers (Reference Town, Waddington, Walden and WarrenTown and others, 2008). On the other hand, the absence of any melting over the Antarctic plateau (Reference ComisoComiso, 2000; Reference Picard and FilyPicard and Fily, 2006), the relatively low heat conduction towards internal snow layers and the low thermal capacity of snow cause its surface temperature to adjust rapidly to changing atmospheric conditions. Air temperature at the standard level of 2 m above the surface is one of the reference parameters commonly used to describe the climate. However, this parameter cannot be measured using remote-sensing techniques, especially in Antarctica, where extreme surface temperature gradients very often prevail in the atmospheric surface boundary layer. Therefore, snow surface temperature is used as a relevant indicator of the seasonal and interannual evolution of the energy balance of the Antarctic plateau. Snow surface temperature can be reasonably well retrieved from satellites, using infrared or microwave observations, at least under specific weather conditions (e.g. Reference ComisoComiso, 1994; Reference Karbou and PrigentKarbou and Prigent, 2005; Reference Picard, Brucker, Fily, Gallée and KrinnerPicard and others, 2009).
More recent interest in snow surface temperature monitoring and simulation comes from the increasing use of advanced infrared atmospheric sounders in the assimilation process of numerical weather prediction (NWP) systems. In stand-alone mode these sounders can retrieve reasonably accurate atmospheric profiles of temperature and humidity, at least under clear-sky conditions (Reference Gettelman, Walden, Miloshevich, Roth and HalterGettelman and others, 2006). This information is very useful for monitoring the current state of the Antarctic atmosphere, where conventional radio soundings are very scarce, especially over the Antarctic plateau. A more accurate estimate of the state of the atmosphere can be provided by the direct assimilation of the radiances measured by the atmospheric sounder IASI (Infrared Atmospheric Sounding Interferometer) on board the MetOp satellite. However, this requires a very accurate estimation of the surface temperature, directly via a previous forecast (the so-called background or guess), or via the utilization of 1D-Var schemes (Reference Bouchard, Rabier, Guidard and KarbouBouchard and others, 2010). It also requires a good knowledge of the surface emissivity, which is the realistic case for snow since it behaves almost like a black body for the considered wavelengths (Reference Dozier and WarrenDozier and Warren, 1982; Reference WarrenWarren, 1982). Nevertheless, most NWP centers do not exploit the full potential of infrared sounders over snow-covered areas, mainly because of significant errors in their background surface temperature estimate and in cloud detection. An international project, Concordiasi, has been initiated in the framework of the International Polar Year (IPY) for assessing the quality of IASI retrievals over the Antarctic plateau and for improving the assimilation of IASI observations in NWP systems (Reference RabierRabier and others, 2010). This project is based on merging field experiments, satellite observations and extensive use of global and regional meteorological models. The experimental campaign relies on in situ observations, additional radio soundings at several polar stations and superpressure balloons, which were launched from the US McMurdo polar base. More detailed local studies are focused on the Antarctic plateau. Taking advantage of its appropriate features (relatively good spatial homogeneity, location under the swath of many polar-orbiting satellites, high-performance routine observations, strong diurnal cycle in summer), the French/Italian polar base Concordia at Dome C is the focal point of the project, where additional observations and dedicated studies have been carried out. The present paper describes one of these studies, which focuses on assessing the capacity of a coupled snow/atmospheric model to simulate the observed surface temperature and low-level atmospheric temperature and wind profile during an 11 day well-documented period of January 2010. As the first stage, the snow model was run in a stand-alone one-dimensional (1-D) mode, in which its meteorological input-forcing data were provided by local meteorological observations. Since this corresponds to the most favorable case, the comparison between modeled and observed snow surface and near-surface temperatures only assesses the performances of the snow model and the quality of the forcing data. In a second stage, a fully coupled three-dimensional (3-D) snow/atmosphere simulation was performed with a regional meteorological model, in which the standard snow parameterization was replaced by the detailed snow model.
2. Stand-Alone Simulation of Snow Surface and Near-Surface TEmperature at Dome C
2.1. Previous studies with detailed snow models in Antarctica
Different detailed 1-D numerical snow models have been developed during the past few decades, for process studies as well as for operational applications in the field of hydrology or avalanche forecasting. Several studies performed detailed intercomparisons of snow models (Reference SlaterSlater and others, 2001). Reference Essery and YangEssery and Yang (2001) compiled a comprehensive description of a large set of snow models, which has been updated by Reference Armstrong and BrunArmstrong and Brun (2008). The International Commission on Snow and Ice (ICSI) organized the Snow Model Intercomparison Project (SnowMIP) in order to assess the performance of various 1-D snow models under different climate conditions (Reference EtcheversEtchevers and others, 2004). The authors highlight how different options in the representation of some key physical processes impact the quality of the simulations. Several snow models performed reasonably well for all SnowMIP meteorological input datasets, but none of these datasets was representative of polar regions.
There is less experience with snow models in polar conditions. The detailed SNTHERM snow model (Reference JordanJordan, 1991) was used for a 1 year simulation of the snow cover over sea ice at North Pole drift station NP-4 (Reference Jordan, Andreas and MakshtasJordan and others, 1999). An accurate representation of the detailed characteristics of the snowpack required a few adjustments, highlighting the critical impact of the parameterization of turbulent fluxes under atmospheric stable conditions. Reference Dadic, Schneebeli, Lehning, Hutterli and OhmuraDadic and others (2008) performed a 10 day simulation at Summit, Greenland, using the SNOWPACK model. They highlighted the importance of vertical resolution and the model discretization for the initial profile of thermal conductivity. The profile was deduced from densities that were estimated from a high-resolution penetration resistance profile measured with a SnowMicroPen. They recommended a vertical resolution of ∼10 mm to get a realistic simulation of the temperature 30 cm beneath the surface. This study at Summit did not focus on the capacity of the model to solve the energy balance and to simulate the snow surface temperature, probably because it used the measured short- and longwave radiative net fluxes as input data, which strongly constrain the surface temperature. Reference Kuipers MunnekeKuipers Munneke and others (2009) ran an energy-balance model (Reference Van den Broeke, Reijmer, van As, van de Wal and OerlemansVan den Broeke and others, 2005) at Summit, including a detailed scheme to compute the absorption of solar radiation by the uppermost snow layers. They performed a 42 day simulation and made a comprehensive sensitivity study of the different components of the surface energy balance. They highlighted the important impact of radiative transfer in snow on the simulated temperature at 0.5 and 0.75 m depths, and obtained very good simulations from the surface to a depth of 1 m.
Most snow simulations for Antarctica have been performed on relatively large areas or at the local scale, in a context in which input meteorological data were derived from climate simulations or reanalyses (Reference Van de Berg, van den Broeke and van MeijgaardVan de Berg and others, 2008; Reference Picard, Brucker, Fily, Gallée and KrinnerPicard and others, 2009). In such a context, it is sometimes difficult to distinguish whether model errors come from uncertainties in input data or from deficiencies in the snow-model physics (e.g. Reference Dang, Genthon and MartinDang and others, 1997). Detailed snow simulations have been performed at South Pole (Reference Town, Waddington, Walden and WarrenTown and others, 2008) and in Dronning Maud Land (Reference Bintanja and van den BroekeBintanja and Van den Broeke, 1995; Reference Van den Broeke, König-Langlo, Picard, Kuipers Munneke and LenaertsVan den Broeke and others, 2010). Reference Town, Waddington, Walden and WarrenTown and others (2008) obtained a very good simulation of the temperatures, heating rates and vapor pressures in near-surface snow at South Pole, during a 9 year period. However, the observed snow surface temperature was used as the upper boundary condition of the snow model, which avoided the difficulty in solving the energy and mass balances at the snow/atmosphere interface. It must be noted that the South Pole experiences no diurnal cycle, limiting one major source of time variability of the snow surface temperature. The relatively limited experience with snow models over the Antarctic plateau means it is still worthwhile to assess, in detail, the ability of such models to simulate the temporal evolution of snow temperature, at the surface and in the top 50 cm, at a site where enough detailed observations are available. It is also very important to properly simulate the snow/atmosphere coupling, in order to improve forecasts in a NWP perspective and also in global climate models for climate scenarios. Dome C is a particularly convenient site to perform such a study, where detailed and accurate observations have been collected since the construction of the French/Italian polar base, Concordia.
2.2. Regular observations at Dome C
Presently, different groups at Dome C maintain a comprehensive in situ observing system which makes it possible to monitor the atmospheric boundary layer, the radiative budget of the snow/atmosphere interface and the evolution of the snow surface and near-surface layers. The main components of this observing system are:
Boundary layer observations by LGGE (Laboratoire de Glaciologie et Géophysique de l’Environnement). Reference Genthon, Town, Six, Favier, Argentini and PellegriniGenthon and others (2010) present and analyze meteorological observations in the summer of 2008 along a 45 m tower at Dome C. The general set-up is fully described by Reference Genthon, Town, Six, Favier, Argentini and PellegriniGenthon and others (2010), and its main features are valid for the current study. The tower is located ∼700 m from Concordia station, in the upwind direction of the prevailing winds. The observation levels above the surface are 4.1, 11.7, 19.3, 26.9, 34.5 and 44.0 m. Wind, temperature and moisture are monitored year-round with a 10 s time-step, and 30 min averages, maxima, minima and variances are computed and archived. In 2009/10 some changes were made to the 2008 set-up. Vaisala 155 thermo-hygrometers are used instead of Campbell HMP45C. The thermo-hygrometers are still housed in naturally ventilated radiation shields (Campbell URS1), but temperature measurements were doubled at each level, with PT100 thermistors in mechanically aspirated radiation shields (Young 43502). This is because Reference Genthon, Town, Six, Favier, Argentini and PellegriniGenthon and others (2010) identified possible occurrences of radiation-induced biases in the 2008 record. The aspirated temperature measurements do confirm biases in the naturally ventilated records. Differences between naturally ventilated and aspirated air temperatures are often <1 K during the considered period. However, a warm bias, up to 6 K, was recorded on 27 January at 0900 h local time, at a moment when very low wind speeds (<1 m s−1) and clear-sky conditions prevailed. This highlights the importance of using aspirated air temperatures over the Antarctic plateau in summer. In this study, the aspirated temperature measurements are used. Moisture measurements are only available in naturally ventilated shields, but radiation biases are not expected to strongly affect specific humidity.
Radiation observations by ISAC/CNR (Institute of Atmospheric Sciences and Climate of the Italian National Research Council). A dedicated observing system which belongs to the BSRN (Baseline Surface Radiation Network) is operated by CNR (Reference OhmuraOhmura and others, 1998; Reference LanconelliLanconelli and others, 2011), maintaining BSRN’s high-standard quality framework to collect accurate high-frequency observations of upward and downward short- and longwave radiation.
Annual mass balance (LGGE). Traditional precipitation gauges do not work in Antarctica, because nearly all the precipitation is in the form of snowfall, either at very low rates (<10 cm w.e. a−1) in the very cold interior of Antarctica, or in regions where strong katabatic winds blow, inducing much blowing snow, which affects the collection and measurement of snowfall. At Dome C, the mean annual accumulation is <40 mm w.e. a−1, and blowing snow, although not frequent, does occasionally occur.
Internal near-surface snow temperature (LGGE). Snow temperature measurements at Dome Concordia which are used in this work are part of a more complete system which has recorded temperatures every hour at 40 levels from the surface down to 21 m since November 2006. Temperature is measured using 100Ω platinum resistance sensors (IEC751, 1/10 DIN). Calibration between all sensors prior to the experiment resulted, after corrections, in a relative accuracy of ±0.02 K (2σ) and an absolute precision better than 0.1 K. The shallowest 15 probes, from the surface to 2 m depth, were driven 50 cm into a snow-pit wall to reach undisturbed snow. The deeper sensors were lowered into a borehole. The pit and borehole were then backfilled with snow. The data logger was buried >1 m below the surface, and the different sensor wires were carefully separated from each other in order to enhance heat exchange with the surrounding snow and to limit heat conduction towards deeper layers.
Snow pits have been regularly dug during summer campaigns since December 2006. The measured properties include snow density, grain size and type, thermal conductivity and temperature. These measurements provide realistic initial conditions for the snow models.
Although the maximum distance between the different components of the observing system is ∼400 m, the high homogeneity and flatness of the Dome C area make it reasonable to consider these observations as representative of a single point, over which a 1-D numerical snow model can be run and evaluated. However, there exist some sources of space heterogeneity, acting at various scales, like sastrugi and hoar surface layers. They are not represented in the present study and can be considered as additional sources of modeling error.
2.3. Description of the snow model and of its adaptation to Dome C conditions
We use a detailed snow model which was developed by implementing the main features of the Crocus snow model (Reference Brun, Martin, Simon, Gendre and ColéouBrun and others, 1989, Reference Brun, David, Sudul and Brunot1992) into the multilayer ISBA-ES (Interactions between Soil, Biosphere and Atmosphere – Explicit Snow) snow model (Reference Boone and EtcheversBoone and Etchevers, 2001). This hybrid snow model is integrated within the framework of the externalized surface module, SURFEX (Reference Salgado and Le MoigneSalgado and Le Moigne, 2010), which can be run either in a standalone mode, using a time series of prescribed meteorological observations as input data, or in a fully coupled mode (explicit or fully implicit) with an interactive simulation of the atmosphere. The latter mode is used in section 3. In its regular configuration, the snow model has the following main characteristics:
The number and depth of snow layers vary in time and space in order to represent the layering of the snowpack. At a given gridpoint, the vertical discretization is governed by a set of rules, which are designed to develop realistic dynamics of snowpack layering, while preserving high-resolution discretization of the uppermost snow layers. This ensures an optimal computation of thermal diffusion. It is achieved in a similar way to the original Crocus model.
Snowfall, surface melting, bottom melting, compaction, internal melting/freezing and metamorphism are the main processes that control the creation and vanishing of the layers. In this study, the maximum number of snow layers is prescribed to be 20.
The heat diffusion within the snow cover is computed using the implicit backward-difference integration scheme of ISBA-ES.
The thermal conductivity of each snow layer is derived as a function of its density, either as described by Reference AndersonAnderson (1976) or as in the original version of Crocus as a set-up option. In the present study we used the first option.
Water percolation through the snowpack is taken into account using a simple method, assuming vertical flow of liquid water as soon as the actual water content exceeds the irreducible water content, which is expressed as a function of pore volume.
The melting/freezing processes are derived from the heat content evolution in each snow layer.
The snow metamorphism is derived from a set of quantitative laws describing the evolution rate of the type and size of the snow grains in each layer, as in the original Crocus model. At a given time-step, the metamorphism is controlled by the temperature, the gradient of temperature and the liquid water content which prevail in the considered layer. The grain types are described via the dendricity and sphericity of the ice crystals of which they are composed.
The snow albedo is calculated as a function of the grain type, size and age in the top 3 cm of the snow cover, considering a partitioning of incoming solar radiation into three spectral bands ([0.3–0.8], [0.8–1.5] and [1.5–2.8] μm), as in Crocus. The reflectance over the first band (ultraviolet and visible radiation) depends on snow grain type, size and age. The age dependency aims to represent the decrease of snow albedo by impurities from deposition in a very simplified way. The rate of decrease has to be tuned according to the local environment. Over the other two bands (near-infrared radiation), the reflectance depends only on snow grain type and size.
The penetration of solar radiation into the surface snow layers and its absorption are taken into account as a function of snow grain type and size, as in Crocus.
The compaction rate of the snow layers is expressed, as in Crocus, through a Newtonian viscosity which depends on density, temperature, liquid water content and snow grain type and size.
The compaction and the metamorphism of the surface layers during snowdrift events are taken into account in a simplified way, as briefly described by Reference Brun, Martin and SpiridonovBrun and others (1997). Snowdrift is assumed to occur when wind velocity exceeds a threshold value, according to fieldwork carried out by Reference Guyomarc’h and MérindolGuyomarc’h and Mérindol (1998). This threshold value depends on snow surface characteristics. During a drift event, the rates of compaction and rounding of the grains in the surface layer depend on the excess of wind velocity relative to the threshold value. Compaction and metamorphism rates, which are associated with drift events, are propagated to the layers beneath the surface, following an exponential decrease, until it meets a snow layer having a mobility threshold value larger than wind velocity.
In the rest of the paper, this hybrid snow model is named Crocus. The energy and mass exchanges between the surface and the atmosphere are calculated according to the ISBA soil/vegetation model (Reference Noilhan and MahfoufNoilhan and Mahfouf, 1996), which is the general framework for continental surfaces in SURFEX. The turbulent fluxes are calculated by means of the classical aerodynamics formulas, with drag coefficients calculated according to Reference LouisLouis (1979) and modified by Reference Mascart, Noilhan and GiordaniMascart and others (1995). The introduction of a limitation in the Richardson number ensures a minimum of turbulent sensible and latent heat exchanges, even in the case of very stable conditions. In this study, the maximum Richardson number has been set to 0.1 and the snow aerodynamics roughness has been set to 0.001 m for both momentum and heat exchanges. The necessary enhancement of turbulent fluxes over snow under stable conditions has been reported in many previous studies (e.g. Reference Beljaars and HoltslagBeljaars and Holtslag, 1991; Reference Martin and LejeuneMartin and Lejeune, 1998; Reference Jordan, Andreas and MakshtasJordan and others, 1999; Reference Essery and YangEssery and Yang, 2001; Reference EtcheversEtchevers and others, 2004; Reference Kuipers MunnekeKuipers Munneke and others, 2009; Reference Town and WaldenTown and Walden, 2009).
The snow model was initially designed for the simulation of seasonal alpine snowpacks. Consequently, many of the processes described above are not relevant in the extremely cold conditions that prevail at and around Dome C, even in January (surface and near-surface snow colder than −20°C during the considered period). It is obviously the case for all processes associated with the presence of liquid water (wet metamorphism, melting/freezing, surface evaporation and liquid condensation) which are, de facto, never activated during the simulations described below. Crocus includes metamorphism laws. They were established during laboratory experiments that reproduced only the snow conditions encountered in temperate alpine conditions. Thus they are not relevant for the extreme climate conditions that prevail on the Antarctic plateau (Reference Dang, Genthon and MartinDang and others, 1997). However, the evolution rates of snow crystals computed according to these laws are very slow under such low temperatures. On the timescales of the simulations done here, which are limited to an 11 day period, the cold conditions strongly limit the metamorphism rate and there is no significant change in the simulated snow microstructure. Consequently, it has not been necessary to tune the metamorphism laws or to turn them off. Taking into account the exceptionally clean atmosphere over the Antarctic plateau, the aging coefficient, which partially controls the albedo evolution in the visible part of the solar spectrum, has been reduced in such a way that the simulated albedo does not significantly change during the simulation. Due to the lack of local observations of the solar spectrum distribution, the downward shortwave radiation has been split into three bands in accordance with an imposed distribution (71%, 21% and 8%).
2.4. Method for assessing the performance of the snow model in a stand-alone mode
To assess the performance of the snow model, we carried out an 11 day simulation of the top 1 m of the snowpack using input meteorological data observed at Dome C between 20 and 30 January 2010. The modeled snow temperature profile has been compared to local observations, with particular attention to snow surface temperature. The meteorological observations used as input data were: air temperature and specific humidity at 4.1 m above the surface; wind speed at 11.7 m; and downward short- and longwave radiations. Because of the absence of significant snowfall events during the period and due to the very low annual snow accumulation at Dome C (<40 mm w.e.a−1; Reference Genthon, Town, Six, Favier, Argentini and PellegriniGenthon and others, 2010), precipitation has been neglected, in spite of the occasional presence of diamond dust.
Figure 1 gives a general overview of the prevailing meteorological conditions. The considered period was characterized by a succession of cloudy and almost-clear-sky days. Cloudy days were more frequent during the first 5 days. They can be easily detected by their impact on the downward longwave radiation, which increases from ∼100 W m−2 under clear-sky conditions to 200 W m−2 under cloudy conditions (mainly the presence of low and medium clouds, considering the high elevation of Dome C, which is located at 3230 m a.s.l.). It must be noted that the downward shortwave radiation is proportionally much less affected by clouds than longwave radiation, due to the particular optical properties of clouds over the Antarctic plateau. Very thin patchy cirrus clouds were often present during the less cloudy days. Snowdrift events are rare at Dome C in summer, due to very frequent calm conditions (Reference Genthon, Town, Six, Favier, Argentini and PellegriniGenthon and others, 2010), but they occur occasionally. During the simulation period, we did not observe any significant drift event, avoiding a dramatic and rapid change in snow surface characteristics. The initialization of the temperature profile came from the measurements of the thermistor chain at the start of the simulation. Since the upper thermistor is located 23 cm below the surface, the initial profile of the top layers has been uniformly set to −30°C, very close to the upper sensor temperature. Three different density profiles were available from snow pits dug before the start of the simulation. They are characterized by a significant spatial variability, which is mainly due to the formation of sastrugi during past snowdrift events. Such a variability is a typical feature of a large part of the Antarctic plateau. Considering this important variability and the impossibility of collecting a density profile in the vicinity of the thermistor chain without disturbing the observations, density has been assumed to increase regularly in depth from a value of 300 kg m−3 at the near surface (10 cm below the surface) to 375 kg m−3 at 10.3 m depth, which is the maximum depth of this simulation. The range 300–400 kg m−3 has been commonly used in previous studies to describe near-surface snow density over the Antarctic plateau (e.g. Reference Brucker, Picard and FilyBrucker and others, 2010). A layer of very loose snow was present at the surface, with crystal shapes similar to hoar crystals. Its exact depth was difficult to measure and was neither homogeneous nor constant. It was typically ∼1–2 cm deep. Considering the extreme difficulty of characterizing such a loose layer, and considering the important impact of low-density insulating snow layers on heat diffusion (Reference Dadic, Schneebeli, Lehning, Hutterli and OhmuraDadic and others, 2008), we tested different profiles of density in the top 10 cm, preserving a regular increase up to 300 kg m−3. Their impact on the simulation will be discussed later. The initial vertical discretization was set in order to have fine resolution close to the surface, to represent the diurnal cycle in detail, while keeping the maximum number of numerical layers below 20. Table 1 describes the initial profile of density and temperature and the corresponding thermal conductivity calculated by the snow model. Considering the short simulation period and the uncertainties in snow metamorphism processes over the Antarctic plateau, the present study does not consider the evolution of snow microstructure. However, it was necessary to initialize the snow grain type, size and age of the top 3 cm of snow in order to get an initial albedo in the range [0.80, 0.81], as observed by the BSRN observing system during the period. During the simulation, we considered a total snow depth of 10.3 m, in order to accurately simulate the thermal inertia and conductivity of the deeper snow layers.

Fig. 1. Time series of observed downward longwave radiation (solid curve) and shortwave radiation (dashed curve), air temperature (4.1 m above the surface) and wind velocity (11.7 m above the surface).
Table 1. Initial state of the simulated snow cover

2.5. Results of the stand-alone simulation
The reference series of observed snow surface temperature has been deduced from the observed upward and downward longwave radiation (BSRN observing system), assuming snow emissivity equal to 0.99. Particular attention has been paid to the reliability of these observations, by comparing them to the surface temperature measured by three other instruments: manual measurements, MODIS (Moderate Resolution Imaging Spectroradiometer) surface temperature and a ground-based infrared radiometer. The different surface temperatures recorded by these four different methods are compared in Figure 2, which leads to the following observations:
Manual measurements. Even taking care with shading and continuously moving the probe of the electronic thermometer (DOSTMANN electronic P655/LOG) at the surface until it reaches its equilibrium temperature, the accuracy of manual measurements is limited. This is especially true when loose snow is present at the surface and under high solar irradiance, which was the case at the time of the manual measurements. Considering these limitations, the comparison with the BSRN surface temperature is quite reasonable. The largest differences are ∼5 K, with higher temperatures collected using the manual method at higher solar elevation angle, which is an expected effect of probe heating by solar radiation.
Infrared radiometer. We set up an IR120 Campbell thermometer at 25 m above the surface on the tower, looking at an unperturbed snow area in the so-called Dome C clean area. The instrument ran for 8 days (21–29 January). It was placed in a heated shelter to ensure thermal stability. The instrument acquired snow temperature data every minute in a routine mode of continuous surface temperature measurements. The main task was to keep the window free of frost and rime. In satellite evaluation mode, we adjusted the viewing angle of the instrument to correspond to the IASI satellite elevation. This was done only under clear-sky conditions and for viewing angles close to nadir. It necessitated a change in the targeted snowpatch from time to time, without any visible disturbance in the recorded series. The agreement between these measurements and BSRN surface temperature was generally good, except during some nights when higher surface temperatures were recorded by the infrared thermometer than the BSRN surface temperature (difference up to 3 K). The difference could be linked to the higher location of the infrared thermometer (25 m above snow surface instead of 2 m), implying an increased sensitivity to the temperature of the surface boundary layer, especially during the occasional foggy periods.
MODIS surface temperature. Surface temperatures were extracted from MODIS MOD11_L2 and MYD11_L2 (version 5) products. The retrievals of surface temperature result from the combination of the brightness temperatures at two bands (11.03 and 12.02 μm) using the generalized split-window land surface temperature algorithm (Reference Wan and DozierWan and Dozier, 1996) and assuming emissivity values of 0.992 and 0.99 at 11.03 and 12.02 μm. Only cloud-free values with the highest quality or declared as ‘fairly calibrated’ were retained. MODIS surface temperatures compare reasonably well with BSRN during the warmest time of the day (0600–1800 h). The bias is negligible and the rms difference is only 1.0 K. In contrast, during the coldest periods MODIS temperatures are lower than BSRN temperatures almost every day. The difference is ∼1.7 K on average and can be up to 5 K. A possible cause for this difference could be the difference in resolution between MODIS (1 km) and the other measurements (a few meters). However, all of the MODIS pixels in the vicinity of Dome C show similar variations, which confirms the apparent homogeneity of the area resulting in homogeneous surface temperature. We have no other explanation for this systematic error and are unable to incriminate any datasets. It is worth noting that the cloud algorithm used in the MODIS product performs well between noon on 24 January and noon on 25 January, when the sky was occasionally overcast. Only a few data are available during this period, but they seem to be accurate, which indicates clear-sky conditions prevailed during these MODIS overpasses.

Fig. 2. Comparison between different observations of snow surface temperature: BSRN longwave radiation retrieval (black); infrared thermometer (blue); manual measurements (green); MODIS retrievals (red).
Taking into account the limitations of the different instruments, the BSRN surface temperature behaves very coherently with most of the other measurements, except during the night-time periods. During these periods, BSRN surface temperature is generally between the MODIS and infrared thermometer temperatures. Therefore, for the remainder of the paper BSRN surface temperatures are considered as the reference observations, against which the simulations could be adequately compared. From here on we define the modeled snow surface temperature as the temperature at the middle of the top numerical snow layer, which is 0.75 cm below the surface. This could involve some uncertainties in the comparison between the observed and the modeled temperatures, especially in the case of strong temperature gradients.
Figure 3 compares the modeled snow surface temperature with the observations. With a bias equal to +0.05 K, a correlation equal to 0.983 and a root-mean-square (rms) equal to 1.16 K, the present simulation performs well. It is in the range of the results obtained by the six snow models that performed best during the SnowMIP project (Reference EtcheversEtchevers and others, 2004). Such a comparison is questionable, because SnowMIP simulations were performed over much longer periods (several months). Nevertheless, it is very encouraging, since the computation of the energy balance of the snow cover over the Antarctic plateau is still recognized as a major scientific challenge (Reference Town, Waddington, Walden and WarrenTown and others, 2008). The short duration of the present simulation could favor such a performance, but it must be noted that the period considered is characterized by a significant diurnal amplitude (16 K, on average) and by variable meteorological conditions, due to frequent changes in cloudiness and wind speed. In summary, modeled temperatures are higher than those observed at night and lower at midday. Largest differences were ∼4 K and occurred at night, especially on 21 January. The height of the level at which the input air temperature and wind velocity were measured (4.1 and 11.7 m, respectively) could partially explain such differences, especially at night when very strong temperature gradients form in the surface boundary layer of the atmosphere.

Fig. 3. Comparison between observed (solid red curve) and modeled (dashed blue curve) snow surface temperature.
Figure 4 shows the daily averaged contribution of the different terms to the surface energy balance. As expected, short- and longwave net fluxes are the major terms. The calculated turbulent sensible heat flux is very low, when averaged on a daily time-step. Indeed, the instantaneous fluxes alternate between positive values (heat towards snow surface, up to 25 W m−2) at night and negative values during midday (heat towards the atmosphere, up to −55 W m−2). It must be noted that the daily averaged sensible heat flux shows larger negative values during cloudy days (24 and 25 January). This is because a higher downward longwave radiation is only partially balanced by a lower downward shortwave radiation. This induces higher surface temperatures than during less cloudy days, which enhances the turbulent fluxes and hence limits snow warming. It must be noted that the latent heat balance over the 11 day simulation is close to zero but negative, which means that the model calculates somewhat more snow sublimation than hoar deposition. With a simulated average value around −1 W m−2 and instantaneous values ranging from +2 W m−2 at night to −8 W m−2 at noon during the simulation, it is even hazardous to conclude whether the average latent flux is positive or negative. The simulated value corresponds to a daily sublimation of ∼0.03 mm w.e., a third of the mean daily accumulation rate. Since there are no instruments at Dome C or at similar locations which would be able to observe such a low sublimation, we can only conclude that the stand-alone simulation cannot explain the presence of the observed surface loose snow layer by a significant hoar deposition.

Fig. 4. Time series of the daily averaged net fluxes simulated by the snow model, with the turbulent sensible heat flux in green, the turbulent latent heat flux in violet, the net longwave radiation in blue and the net shortwave radiation in red. The corresponding total net flux is represented by the solid black line. Positive values correspond to heat fluxes oriented towards snow.
The total net flux at the surface is positive and equal to 1.5 W m−2. This is too weak a flux to compensate for the cooling from the colder deep snow layers, which is around 2 W m−2 (gradient of ∼6.5 K m−1 at the depth of 2 m, where thermal conductivity is ∼0.33 W m−1 K−1). This explains why the top surface meter experiences cooling at the end of the period. It is especially obvious at the end of the period when clear-sky conditions prevail and when the sun already shows a significant decline, which is typical of late-summer conditions (see Fig. 1).
Figure 5 shows a comparison of the modeled near-surface snow temperature with the observations. The model performs reasonably at all depths. The modeled downward propagation of the diurnal waves matches the observed change in phase and amplitude, down to 43 cm depth, with an overestimation of the amplitude which is more obvious at 23 cm depth. At 53 cm depth, the modeled wave shows a start of delay in its phase, which is difficult to characterize since its amplitude is only ∼0.2 K. The difference probably comes from uncertainties in the actual density profile, especially between depths 40 and 60 cm, in links with the natural variability of density profiles, mentioned above, or with very local disturbances of snow density during the installation of the sensors. It could also stem from the computation of thermal conductivity in the model, which does not take into account the specific microstructure of snow crystals which develop in near-surface snow layers at Dome C. The uncertainty in the exact location of the thermistor chain could also be invoked, in links with the accumulation of snow since its installation. However, this last hypothesis should have a stronger impact on the modeled temperature in the upper layers. The overall quality of the simulation is encouraging, since it shows a smaller bias than that obtained at 30 cm depth by Reference Dadic, Schneebeli, Lehning, Hutterli and OhmuraDadic and others (2008) at Summit, during a simulation of a similar duration. However, our simulation does not perform as well as that of Reference Kuipers MunnekeKuipers Munneke and others (2009), at least regarding the rms error of the modeled snow surface temperature. This could stem from a simpler representation of radiative transfer in snow (3 spectral bands instead of 118 and deeper numerical layers). Our simulation demonstrates that the input meteorological data, which are routinely measured at Dome C by LGGE and PNRA (Italian Programma Nazionale di Ricerche in Antartide) groups, are very reliable. It consolidates our confidence in the quality of the modeled surface temperature and in the computation of the energy exchanges.

Fig. 5. Comparison between observations (solid curves) and stand-alone simulations (dashed curves) of snow temperature at different depths in the top meter of the snowpack. Top panel: blue is −23 cm; brown is −33 cm; red is −53 cm; green is −73 cm. Bottom panel: blue is −28 cm; brown is −43 cm; red is −63 cm; green is −83 cm.
However, as previously noted, the loose snow layer which forms at the surface cannot be easily characterized. Different tests have been performed with higher snow density at the surface. All the corresponding simulations did not perform as well as the presented one. Some of them even showed a full out-phasing of the diurnal wave at depths below 40 cm. This highlights the importance of such surface layers in the control of heat diffusion towards deeper layers. The process of their formation is still an open issue.
This section of the paper has demonstrated that Dome C is equipped with very reliable instruments, which constitute a comprehensive framework for monitoring the joint evolution of the near-surface snowpack and of the atmospheric surface boundary layer. Detailed snow models using these observations as input data can reasonably simulate the evolution of surface temperature and the evolution of the downward propagation of diurnal heatwaves within the near-surface snowpack. This is at least true under the meteorological conditions experienced during the considered period. This is a sound basis for testing the capacity of coupled snow/atmosphere models to simulate the processes that govern the energy balance of this system, which is representative of a large part of the Antarctic plateau.
3. Coupled Simulation of Snow/atmosphere Interactions
The physical properties of snow strongly differ from those of any other type of terrestrial surface. Due to its high albedo, its low thermal capacity and low conductivity, the presence of snow on the ground has a very high impact on the evolution of the surface boundary layer. It generally induces a rapid cooling and stabilization of the lowest layers of the atmosphere, which drastically impacts the energy, mass and momentum exchanges, not only at the surface but over the whole troposphere. In order to take into account the associated processes, snow parameterizations or simple snow models have been developed and implemented into meteorological and climate models. However, the representation of snow is still relatively simple in most meteorological and climate models, mainly to save computational cost or comply with initialization or assimilation constraints. Pioneering works were initiated for implementing a detailed representation of snow processes in global or regional climate models (Reference Brun, Martin and SpiridonovBrun and others, 1997; Reference Liston, Pielke and GreeneListon and others, 1999; Reference Gallée, Guyomarc’h and BrunGallée and others, 2001). Antarctica is the only continent on Earth where snow and ice strongly impact the energy and mass exchanges between the surface and the atmosphere all year long. Reference Gallée and GorodetskayaGallée and Gorodetskaya (2008) have shown that the MAR (Modéle Atmosphérique Régional) regional climate model, which includes a detailed snow model, proved able to realistically simulate the winter characteristics of the atmosphere around Dome C, during a 4 year simulation. Here we complete Gallée’s and Gorodetskaya’s work by focusing on the ability of a high-resolution coupled model to simulate, in detail, the diurnal cycle of the snow/atmosphere interface.
3.1. Description of the meteorological model and configuration of the simulations
In order to simulate the energy and mass exchanges between the snow cover and the atmosphere around Dome C, we used the AROME limited-area model (Reference SeitySeity and others, 2011). This model is the non-hydrostatic operational meteorological model used by Météo-France to produce real-time high-resolution forecasts over France. Its code is part of the IFS/ARPEGE library. Its dynamics and physics benefit from cooperative developments between Météo-France, the European Centre for Medium-Range Weather Forecasts (ECMWF), the ALADIN/HIRLAM consortium (meteorological services from European and North African countries) and the scientific community developing the Meso-NH atmospheric model. The main characteristics of the operational physics package are: radiation in the atmosphere is solved using a two-stream approximation in model columns with a code that is very close to the ECMWF operational version; Fouquart–Morcrette in visible bands and RRTM (Rapid Radiative Transfer Model) in infrared bands; turbulent mixing is based on a prognostic turbulent kinetic energy with the Cuxart 1-D scheme and a mixing length from Reference Bougeault and LacarrèreBougeault and Lacarrère (1989) for the computation of the exchange coefficient; explicit cloud microphysics are computed using the Meso-NH ‘ICE3’ scheme, which computes the evolution of six water species (water vapor, cloud liquid droplets, precipitating liquid rain, cloud ice, precipitating icy snow and precipitating mixed ice/water graupel); subgrid cloud effects are taken into account through the ‘shallow convection’ scheme of Reference Pergaud, Masson, Malardel and CouvreuxPergaud and others (2009).
We set up a 625 km × 625 km configuration of the model, centered around Dome C, at the operational resolution (2.5 km horizontal resolution and 60 vertical layers). This geometry puts the first three atmosphere levels around 8.5, 27 and 51 m above the snow surface at the Dome C central gridpoint, which is located in the model at 3229 m a.s.l. We did not change the regular physics package, except for the representation of snow-cover processes. In its standard configuration, AROME uses a snow parameterization developed by Reference Douville, Royer and MahfoufDouville and others (1995a,Reference Douville, Royer and Mahfoufb), which is a composite snow/soil/vegetation model. We replaced it by the Crocus snow model. To achieve the replacement of the single-layer snow parameterization by a detailed multilayer snow model, we took advantage of the framework offered by the externalized surface module SURFEX and by the ISBA-ES algorithms, into which Crocus has been implemented. This software architecture achieves a full explicit coupling between the atmosphere and the snow cover, through a coherent exchange of energy and mass fluxes between both components at every time-step. This framework made it possible to use exactly the same configuration of Crocus in the coupled mode as in the standalone mode.
From 20 to 30 January, we performed a series of 11 consecutive 24 hour forecasts with the non-hydrostatic model AROME in dynamical adaptation mode. In order to assess the performance of the snow model in coupled mode, the state of the modeled snow cover was cycled along all the 11 series of 24 hour runs. This means that all snow variables (temperature, density, grain-type, grain-size, grain-age and liquid water content profiles), which were calculated at the end of a 24 hour simulation at every gridpoint, were used as the initial state of the snow cover for the next 24 hour simulations. This configuration inhibits any reinitialization of the snow cover, which can freely evolve over the whole domain and all through the 11 day simulation, under the sole influence of the energy and mass fluxes which are exchanged with the modeled atmosphere. At the beginning of the first 24 hour simulation, on 20 January, the initial state of the snow cover was the same as the initial state of the 1-D stand-alone simulation described in section 2 (Table 1). Given the high homogeneity of the Dome C area, the same initial state of the snow cover was used for all gridpoints.
The lateral boundary conditions were provided by the ARPEGE global NWP model. We used a tuned version of ARPEGE, which has been specifically designed for studies for IASI assimilation over Antarctica (Reference Bouchard, Rabier, Guidard and KarbouBouchard and others, 2010). This spectral model has a stretched geometry, which enables enhanced horizontal resolution over a given area (and a coarser resolution at the antipodes), while limiting the computing cost. In this study, the stretching pole was moved to Dome C, which ensures a resolution of ∼10 km over a large part of the Antarctic plateau. A 4D-Var assimilation (Reference Courtier, Thépaut and HollingsworthCourtier and others, 1994; Reference Rabier, Järvinen, Klinker, Mahfouf and SimmonsRabier and others, 2000) was run four times a day, each assimilation covering a 6 hour time window. The stretched geometry was also used for the nonlinear runs in the 4D-Var assimilation, whereas minimizations were performed on a regular grid. This version of ARPEGE assimilates the available operational observations plus additional IASI observations over snow and sea ice. The successive ARPEGE analyses obtained at 00.00 UTC provided the initial states for the coupled limited-area model AROME, while the ARPEGE model forecasts provided its lateral boundary conditions. It must be noted that routine radio soundings are made once a day at Dome C, at 12.00 UTC (2000 h local time). This means that the initial states of the AROME model never directly benefited from local conventional upper-air observations during the considered period. This avoids an artificial source of positive skill, which would have limited the representativeness of the coupled model results.
3.2. Coupled simulation results
To assess the quality of the coupled simulation, we made the same comparisons as during the stand-alone simulation (snow surface and near-surface temperature), plus additional comparisons with observations collected in the atmosphere boundary layer. We focused on the meteorological variables that contribute the most to the surface energy balance, as discussed above: surface long- and shortwave radiation, which control the radiative fluxes, and air temperature and wind velocity in the surface boundary layer, which control the turbulent heat fluxes. Table 2 presents the spatial mean value and standard deviation of these variables over a 1° latitude × 4° longitude area centered around Dome C. These values were obtained by averaging the hourly time series of the instantaneous spatial means and standard deviations during the entire simulation. The very low values of the spatial standard deviation show that the coupled model captures the very high homogeneity of the Dome C area. This is not surprising, since there are no significant differences in the physiography of the area and since we imposed a homogeneous state of the snowpack at the beginning of the simulation. Because of this homogeneity, it makes sense to directly compare the observations collected at Dome C with the model outputs at the central gridpoint.
Table 2. Spatial variability of the coupled simulation. The mean value and the standard deviation are calculated by averaging during the entire simulation the hourly time series of the instantaneous spatial means and standard deviations over a 1° latitude × 4° longitude area centered around Dome C

Figure 6 compares the modeled variables at the Dome C gridpoint with the corresponding observations. The modeled temperature is diagnosed by AROME at the same level as the observation (4.1 m above surface) using its standard boundary layer diagnosis scheme. The modeled wind velocity is the 10 m wind diagnosis while the observation is at level 11.7 m. The largest departures occurred around 22, 24–25, 27 and 30 January. Except on 27 January, and maybe on 25 January, these differences are caused by a poor simulation of cloudiness, which can be inferred in Figure 6 from the mismatch of the longwave downward radiation. Longwave bias is negligible (−0.2 W m−2), but rms error is 28 W m−2 and correlation is only 0.05 over the whole period. On 22 and 30 January, low clouds form in the model, but not in reality, which induced excessively high temperatures in the model. The opposite happened on 24–25 January. The large error in the minimum air temperature on 27 January is probably linked to an overestimation by the model of the extremely low wind speed observed at the end of the night. It is difficult to attribute the departure in surface temperature on the 25 January, since it combines errors in longwave radiation, wind speed and air temperature.

Fig. 6. Comparison between the observed (solid curve) and the corresponding coupled model simulation (dashed curve) for downward long- and shortwave radiation (blue and red, respectively), air temperature and wind velocity. Both observed and modeled air temperature are at level 4.1 m. Observed wind velocity is at level 11.7 m while modeled wind velocity is at level 10 m.
Figure 7 shows plots of the snow surface temperature simulated by the coupled model against the observed values and against the previous results from the standalone simulation. With a bias equal to +1.29 K, an rms error equal to 3.54 K and a correlation equal to 0.86, the coupled simulation produces a lower-quality performance than the stand-alone simulation but it is still reasonable. The largest differences are linked with errors in the cloudiness, as discussed above.

Fig. 7. Comparison between observed snow surface temperature (solid black curve) and surface temperature modeled by the coupled snow/atmosphere model (red dashed curve) and by the stand-alone snow model (blue dashed curve).
Figure 8 compares the modeled near-surface snow temperature with the observations. Even if the above-mentioned errors in cloudiness sometimes induce an error in snow surface temperature, the impact on the near-surface temperature is limited and the coupled snow model is able to simulate a realistic propagation of the diurnal heatwave into the snowpack. It is encouraging to note that there is no drift in the temperature departure, in spite of the fact that the state of the snow cover has freely evolved throughout the 11 day simulation without any reinitialization or assimilation. This is because there is almost no bias in the modeled longwave radiation, in spite of significant errors in the instantaneous values.

Fig. 8. Comparison between observations (solid curves) and coupled simulations (dashed curves) of snow temperature at different depths in top meter of the snowpack. Top panel: blue is −23 cm; brown is −33 cm; red is −53 cm; green is −73 cm. Bottom panel: blue is −28 cm; brown is −43 cm; red is −63 cm; green is −83 cm.
Figure 9 shows a comparison between the modeled and observed vertical profiles of the diurnal amplitude of temperature from the surface to the top of the 45 m tower. At sensor levels higher than the first native level of the meteorological model (8.5 m), the modeled temperatures were computed by a linear projection of model outputs. At lower levels (0.5, 2 and 4.1 m), the modeled temperatures were computed by the boundary layer diagnosis scheme of the meteorological model. Observations at levels 0.5 and 2 m were collected under naturally ventilated radiation shields. Therefore, some biases are expected (Reference Genthon, Town, Six, Favier, Argentini and PellegriniGenthon and others, 2010). Even though the representation of turbulent fluxes in AROME was not tuned for Antarctic conditions, the decrease of the average diurnal amplitude with elevation is quite well reproduced. This is encouraging, since meteorological models have difficulties in predicting turbulent fluxes under very stable conditions (e.g. Reference Anderson and NeffAnderson and Neff, 2006; Reference Sukoriansky, Galperin and PerovSukoriansky and others, 2006; Reference Town and WaldenTown and Walden, 2009; Reference Genthon, Town, Six, Favier, Argentini and PellegriniGenthon and others, 2010). Alternate formulations of turbulent fluxes over snow and ice have been reviewed by Reference AndreasAndreas (2002) and some of them have been implemented with significant impact over Antarctica (Reference King, Connolley and DerbyshireKing and others, 2001). They could be tested in further versions of our coupled model, but that seems a lower priority than improving the cloud simulation.

Fig. 9. Comparison between the observed (solid red curve) and modeled (dashed blue curve) vertical profiles of the diurnal amplitude of temperature from the surface to the top of the 45 m tower, averaged over the entire 11 day simulation. The modeled data are from the Dome C gridpoint.
Figure 10 shows a comparison between the modeled and observed vertical profiles of the average wind speed from the surface to the height of the third atmospheric layer (51 m). To make the comparison easier, logarithmic functions have been fitted to the observed and modeled data. The agreement is reasonable, but indicates that the coupled model probably uses a roughness length for momentum fluxes above snow which is slightly too large. This wind profile comparison confirms the good behavior of the coupled model at the snow/atmosphere interface, even under very stable conditions.

Fig. 10. Comparison between the modeled (blue circles) and observed (red circles) vertical profiles of the average wind speed from the surface to 51 m, averaged over the entire 11 day simulation. The modeled data are from the Dome C gridpoint. Their height corresponds to the native vertical grid. Blue dashed curve is logarithmic fit to the modeled data. Red dashed curve is logarithmic fit to the observed data.
4. Discussion
The context of our study is convenient for investigating the origin of the main errors which have been detected in the snow/atmosphere coupled simulation, with particular attention to longwave radiation. The important point is that we ran exactly the same configuration of the snow model and used the same initial snow profile in the stand-alone simulation as in the coupled simulation. Because of the rather short duration of the simulation and because of the very cold surface and near-surface snow temperatures, no significant changes occurred in the radiative and thermal properties of the uppermost snow layers. Since the standalone simulation performed well and since the coupled simulation of the snow surface temperature shows neither a large bias (<1.3 K) nor a significant trend, the errors cannot come from the amplification throughout the 11 day period of feedbacks between the snow cover and the atmosphere. This hypothesis is confirmed by the fact that errors were more frequent during the cloudy first half of the studied period than during the less cloudy second half. Several studies have highlighted the specific behavior of cloud formation over the Antarctic plateau and the importance of corresponding adjustments in the meteorological models’ microphysics schemes (e.g. Reference Fogt and BromwichFogt and Bromwich, 2008; Reference Gallée and GorodetskayaGallée and Gorodetskaya, 2008). Since the AROME model has never been tested before over Antarctica, we compared its modeled downward longwave radiation with the corresponding outputs of different research and operational models: AMPS (Antarctic Mesoscale Prediction System), which is designed for high-resolution real-time forecast over Antarctica (Reference Powers, Monaghan, Cayette, Bromwich, Kuo and ManningPowers and others, 2003; Reference Bromwich, Monaghan, Manning and PowersBromwich and others, 2005); ECMWF and the Antarctic stretched version of ARPEGE, which benefit from a very advanced high-resolution 4D-Var assimilation; and Meso-NH which is a high-resolution research meteorological model. These models run in different contexts, but all the data in Figure 11 correspond to short-range forecasts (up to 24 hours), starting every day from analyses or initializations at 00.00 UTC. The values were extracted at the gridpoint closest to Dome C. Despite the fact that these models exhibit large differences, either in their cloud microphysics or in their initialization schemes, it is surprising that they experience very similar deficiencies during the considered period (Meso-NH outputs are not shown in Fig. 11; they are very similar to AROME outputs). It should be noted that the apparent better skill of AROME is mainly due to an artifact in its initialization process which starts without any clouds at 00.00 UTC every day. This highlights the difficulty that weather prediction and research models face in the forecast of clouds over the Antarctic plateau, even on sites where routine radio soundings are available. Even if radio soundings are made only at 12.00 UTC at Dome C, and thus do not directly impact our initial atmospheric conditions, the assimilation process involves a cycling in time, and 12.00 UTC radio soundings of the previous day should still have a positive impact on the 00.00 UTC analysis. Considering the results of the different models, we did not try to tune the AROME microphysics scheme, because a sound improvement of the main errors in our simulation requires either a better analysis of the initial state of the atmosphere (mainly through better use of the assimilation system) or more adequate microphysics schemes for polar conditions. It is likely that both aspects are of similar importance.
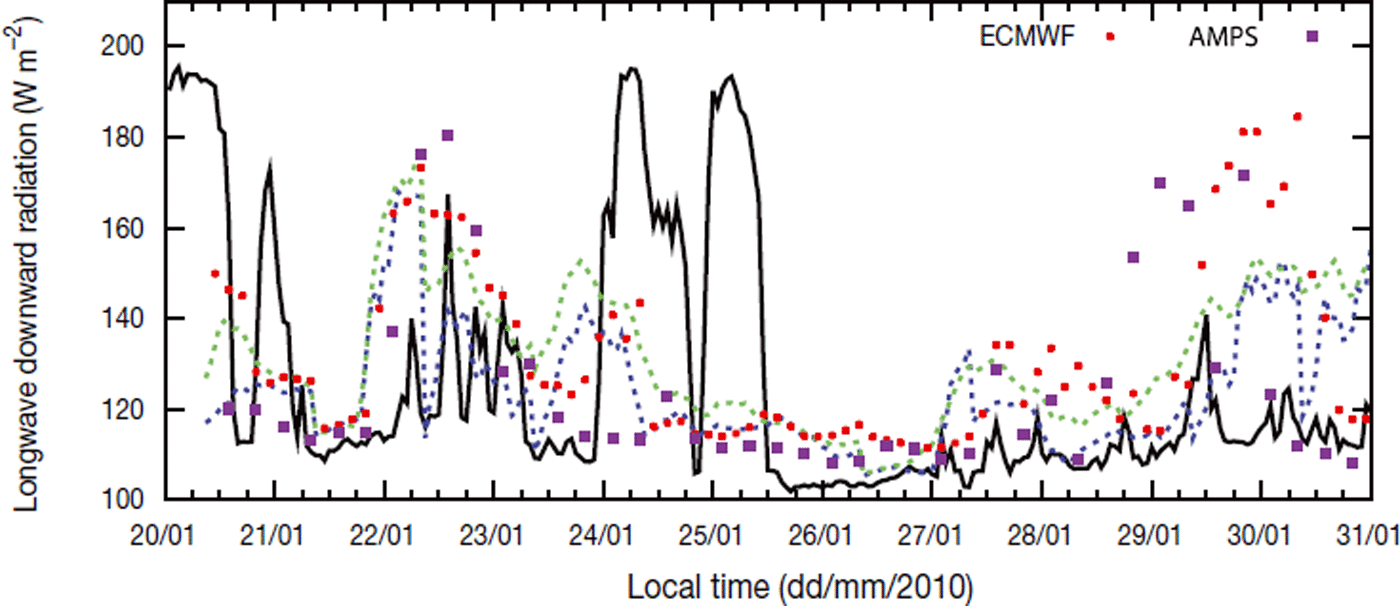
Fig. 11. Comparison between the observed (black solid curve) downward longwave radiation and the corresponding outputs of various meteorological models: Crocus/AROME coupled model (blue dashed line); Antarctic version of ARPEGE (green dashed line); operational ECMWF (red round points); AMPS (violet square points). Time resolution is 1 hour for ARPEGE and AROME, 3 hours for ECMWF and 6 hours for AMPS.
In order to isolate the negative impact of the poor performance in cloud simulation, we plotted (Fig. 12) the modeled surface temperature against the observations over the less-cloudy 4 day period, from 26 January 0000 h local time to 30 January 0000 h local time. Even if the modeled downward longwave radiation does not perfectly match the observations, snow surface temperature is quite well modeled: bias is +0.69 K, rms error is 1.8 K and correlation is 0.97. This shows that the coupled model correctly computes the energy exchanges at the snow/atmosphere interface and simulates the joint evolution of the top snow layers and of the atmospheric boundary layer quite well.

Fig. 12. Comparison between observed snow surface temperature and surface temperature modeled by the coupled snow/atmosphere model from 26 January 0000 h to 30 January 0000 h. The dashed line is the corresponding regression line.
5. Conclusions and Outlook
The performance of the stand-alone 11 day simulation of the near-surface snowpack shows that Dome C is equipped with an in situ observing system that is very comprehensive and of high quality. This makes it possible to study in detail the physical processes which control the energy exchanges between the snow cover and the atmosphere, at a location which is very representative of a large part of the Antarctic plateau. The quality of the stand-alone simulation is very sensitive to the initial state of the snow cover, especially regarding the surface radiative properties and the detailed profile of density and thermal conductivity in the top few centimeters. During the considered period, the surface layer was loose and difficult to characterize with classical instruments. The present study has benefited from the fact that these critical parameters do not evolve significantly during such a short period. It is clear that a similar but longer simulation, over a year or even a month, would suffer from a poor knowledge of the processes that govern the formation and the transformation of such loose layers: diamond-dust precipitation, hoar deposition, sublimation, wind erosion/deposition and metamorphism. Its space heterogeneity could also be a limitation for stand-alone snow simulations at different locations or for different seasons. Improving the understanding and simulation of these processes is a major challenge for the future, which is of interest for meteorology, climatology and snow photochemistry over the Antarctic plateau. The coupling of a high-resolution non-hydrostatic atmospheric model with a detailed snow model proved able to simulate a coherent evolution of the near-surface snowpack and of the atmospheric surface boundary layer. This simulation showed no significant bias regarding the snow surface and near-surface temperatures. The downward propagation of the diurnal heatwave into the snow cover has been realistically simulated and the model reproduced particularly well the average decrease of the diurnal amplitude of air temperature from the surface to the top of the 45 m tower. Most of the instantaneous errors came from a poor simulation of cloudiness, which induced significant errors in the simulation of the downward longwave radiation and consequently on snow surface temperature. A comparison with the outputs of various meteorological models shows that they all face similar errors throughout the 11 day simulation, even the model that benefits from a calibration of its cloud microphysics for polar conditions. Our study did not identify whether the errors stem from deficiencies in cloud microphysics or uncertainties in the initial state of the atmosphere. The ongoing Concordiasi project has just finished its intensive observation period. Between September and November 2010, ∼300 dropsondes have been launched over the Antarctic plateau from superpressure balloons. Concordiasi provides a unique framework for assessing the quality of the real-time and delayed analysis of the Antarctic atmosphere and for improving assimilation of the observations collected by the advanced IASI sounder, which are very dense over the Antarctic plateau. There is no doubt that an improved and more intensive assimilation of infrared atmospheric sounders over snow and ice surfaces will improve the real-time analyses and the reanalyses of the Antarctic atmosphere. It should also improve the skill of meteorological models regarding cloud forecasting or, at least, provide better constraints for the improvement of their microphysics schemes. Despite the difficulties we faced with cloud forecasts, the coupling of a state-of-the-art atmospheric model with a detailed snow model has shown a high skill level regarding the forecast of snow surface temperature under clear-sky conditions. This was a necessary condition for further studies on the assimilation of IASI observations in the framework of the Concordiasi project and for improving the snow-cover representation in global or regional Earth system models.
6. Acknowledgements
This work is a contribution to the international Concordiasi project, currently supported by the following agencies: Météo-France; CNES; CNRS/INSU; NSF; NCAR; University of Wyoming; Purdue University; University of Colorado; the Alfred Wegener Institute; the Met Office; and ECMWF. Concordiasi also benefits from logistic or financial support from the operational polar agencies IPEV, PNRA, USAP and BAS, and from BSRN measurements at Concordia. Concordiasi is part of the THORPEX IPY cluster within the International Polar Year effort.
This work was funded by IPEV, under the CALVA project, and by the European Commission’s 7th Framework Programme, under grant agreement No. 226520, COMBINE project. Concordia station at Dome C is jointly operated by IPEV and PNRA. Meteorological instruments on the tower were funded by the French Institut National des Sciences de l’Univers program Equipement-Troposphère-Concordia. ISAC-CNR provided the BSRN radiation data.
We thank L. Moggio who achieved the radio soundings assimilated by ARPEGE, C. Lanconelli who provided the BSRN data, F. Domine and M. Town, who provided the IR thermometer, C. Lac who provided Meso-NH outputs, J. Nicolas who provided AMPS outputs and A. Pellegrini who provided some of the meteorological observations. The AMPS project is funded by UCAR subcontract 20020793.
Open data access to the internal snow temperatures are available on the OSUG website (http://www-lgge.obs.ujfgrenoble.fr/∼picard/).
















