Introduction
The fracturing of brittle heterogeneous material has often been studied at the laboratory scale using acoustic-emission measurements (see, e.g., Reference Johansen and SornetteJohansen and Sornette, 2000; Reference Nechad, Helmstetter, El Guerjouma and SornetteNechad and others, 2005a, for recent observations interpreted using concepts relevant to the present study). These studies reported an acceleration of brittle damage before failure. Acoustic-emission tools have been used at the mesoscale to find precursors to natural gravity-driven instabilities such as cliff collapse (Reference Amitrano, Grasso and SenfauteAmitrano and others, 2005) or slope instabilities (Reference Dixon, Hill and KavanaghDixon and others, 2003; Reference Kolesnikov, Nemirovich-Danchenko, Goldin and SeleznevKolesnikov and others, 2003; Reference Dixon and SpriggsDixon and Spriggs, 2007). The present paper focuses on the acoustic emissions generated by an unstable glacier. To our knowledge, this is the first attempt to use these acoustic emissions to predict the catastrophic break-off of a glacier.
Ice mass break-off is a natural gravity-driven instability, as found in the case of a landslide, rockfalls or mountain collapse. Such glacier break-off represents a considerable risk to mountain communities and transit facilities situated below, especially in winter, as an ice avalanche may drag snow in its train. In certain cases, an accurate prediction of this natural phenomenon is necessary in order to prevent such dangerous events. The first attempt to predict such break-offs was conducted in 1973 by Reference FlotronFlotron (1977) and Röthlisberger (1981) on the Weisshorn hanging glacier. The latter author measured the surface velocity of the unstable glacier and proposed an empirical function to fit the increasing surface velocities before break-off. This function describes an acceleration of the surface displacement following a power law up to infinity at a finite time, t c. Obviously, the real break-off will necessarily occur before t c, but the method gives a good description of the surface velocity evolution until rupture. Recently, following Reference LüthiLüthi (2003) and Reference Pralong, Birrer, Stahel and FunkPralong and others (2005), Reference Faillettaz, Pralong, Funk and DeichmannFaillettaz and others (2008) showed evidence of an oscillatory behavior superimposed on the general acceleration which enables a more accurate determination of the time of rupture. Reference Faillettaz, Pralong, Funk and DeichmannFaillettaz and others (2008) also showed an increase in icequake activity before the break-off. The aim of this paper is to present (1) a careful analysis of these seismic measurements, (2) our conclusions in terms of rupture processes and (3) perspectives for forecasting.
Several studies have shown that glaciers can generate seismic signals called ‘icequakes’. At least five characteristic seismic waveforms have been identified, associated with five different icequake event types: (1) surface crevassing (high frequency, short duration, impulsive onsets; Reference Neave and SavageNeave and Savage, 1970; Reference Deichmann, Ansorge, Scherbaum, Aschwanden, Bernardi and GudmundssonDeichmann and others, 2000; Reference Walter, Deichmann and FunkWalter and others, 2008); (2) calving events (low frequency, long duration, non-impulsive onsets, surface waves; Reference O’Neel, Marshall, McNamara and PfefferO’Neel and others, 2007; Reference NettlesNettles and others, 2008); (3) basal sliding (low frequency, short duration, no surface waves; Reference Weaver and MaloneWeaver and Malone, 1979); (4) iceberg interaction (low frequency, long duration, multiple harmonic frequencies; Reference MacAyeal, Okal, Aster and BassisMacAyeal and others, 2008) and (5) hydraulic transients in glacial water channels (low frequency, emergent onset, absence of distinct S wave; Reference Lawrence and QamarLawrence and Qamar, 1979).
In this study we focus on the seismic activity generated by a cold hanging glacier before its break-off. The crucial features of this type of glacier are (1) there is no sliding at the bedrock and (2) the glacier is entirely cold and there is no water within the ice. Precursory seismic signals were detected, and a change in behavior occurred 2 weeks before the global rupture.
Weisshorn Glacier and the History of Events
The northeast face of the Weisshorn, Valais, Switzerland, is covered with unbalanced cold ramp glaciers (i.e. the snow accumulation is, for the most part, compensated by break-off; Reference Pralong and FunkPralong and Funk, 2006), located between 4500 and 3800 m a.s.l., on a steep slope of 45–50°. In winter, snow avalanches triggered by icefalls pose a recurrent threat to the 400 inhabitants of the village of Randa, located ∼2500 m below the glacier, and to transit routes to Zermatt (Fig. 1). In a compilation of historical records, Reference Raymond, Wegmann and FunkRaymond and others (2003) showed that, despite no seasonal pattern in the events, Randa has been damaged repeatedly during past centuries, always in winter. Among the 19 events recorded since 1636, three caused a total of 51 fatalities and six damaged the village of Randa. The Weisshorn hanging glacier has broken off five times in the past 35 years (1973, 1980, 1986, 1999 and 2005; Reference Raymond, Wegmann and FunkRaymond and others, 2003; two of these events, in 1973 and 2005, were monitored in detail by Reference FlotronFlotron, 1977, and Reference Faillettaz, Pralong, Funk and DeichmannFaillettaz and others, 2008). Prior to the most recent episode, the total volume of the unstable ice mass was estimated at 0.5 × 106 m3 by means of photogrammetry (Reference Faillettaz, Pralong, Funk and DeichmannFaillettaz and others, 2008). Because of the danger to the village of Randa, a monitoring system was installed to alert the population to an impending break-off.
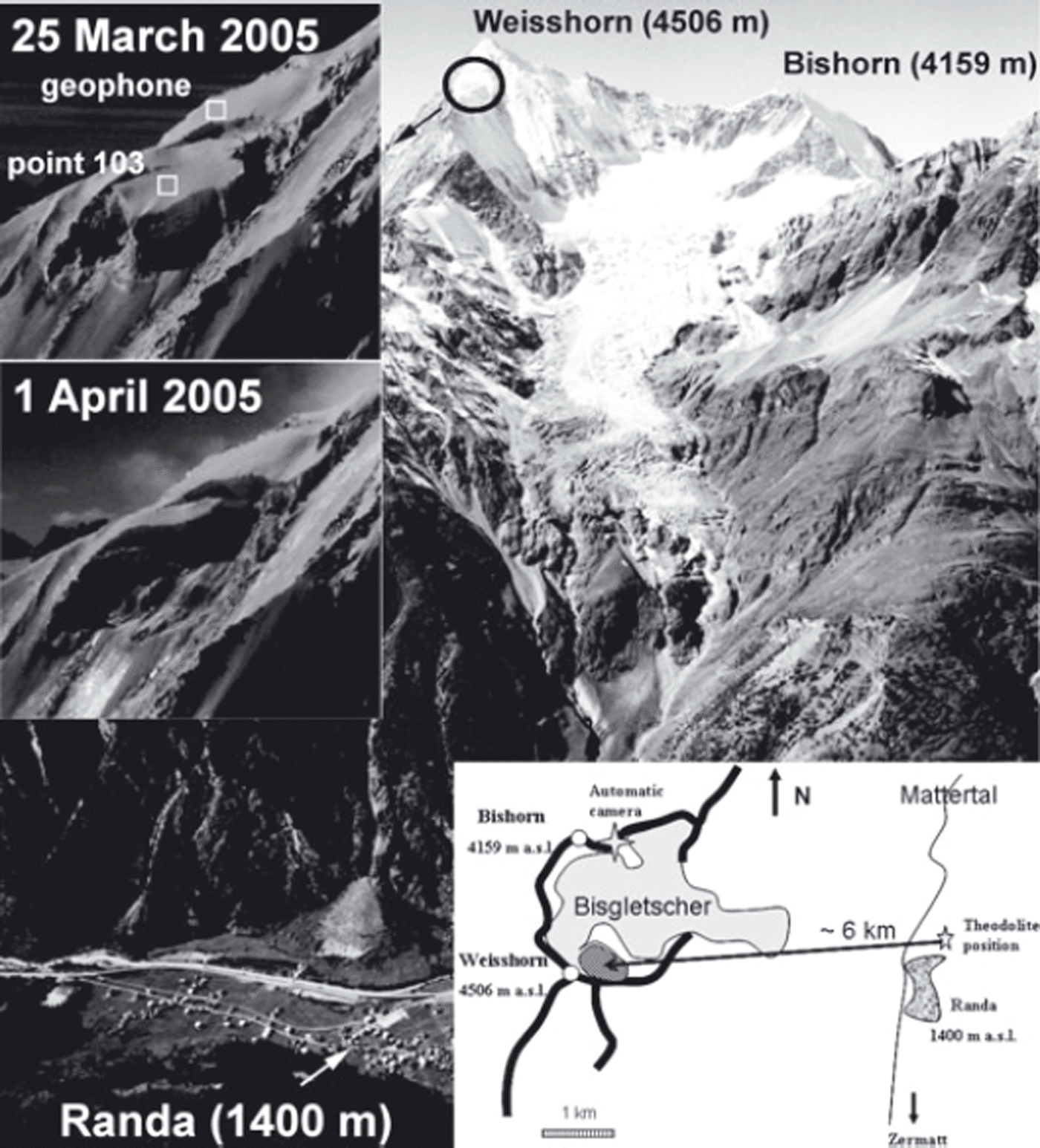
Fig. 1. The east face of Weisshorn with the hanging glacier. The village of Randa and transit routes are visible in the valley. The ellipse indicates the location of the hanging glacier. The left insets show a closer frontal view of the hanging glacier on 25 March 2005 before the second break-off (upper) and on 1 April 2005 after the break-off (lower), including the positions of the geophone and reflector 103 used for displacement measurements. Note that the rupture occurred above the bedrock (∼2 m), within the ice. The bottom right inset gives a general schematic view of the Weisshorn hanging glacier (dashed zone) and the monitoring setting (theodolite and automatic camera). Thick black curves indicate the mountain ridges, and the thin line represents the bottom of the valley.
Methods
Instrumentation
An automatic camera (installed in September 2003 on the Bishorn with a 1 day time lapse; Fig. 1) provided a detailed movie of the destabilization of the glacier. A first break-off occurred on 24 March 2005 (after 26.5 ± 0.5 days of monitoring). Its estimated volume amounted to 120000 m3 (comparable to the 1973 break-off with 160000 m3). On 31 March 2005, a second rupture occurred, during which an estimated ice volume of 400 000 m3 broke off.
A single geophone (Lennartz LE-3Dlite Mkll, three orthogonal sensors, with eigenfrequency of 1 Hz) was installed in firn 30 cm below the surface near the upper crevasse (Fig. 1), in order to record icequake activity before the final rupture. This signal is assumed to describe the crack (or damage) evolution within the ice mass during the failure process. A Taurus portable seismograph (Nanometrics Inc.) was used to record the seismic activity of the glacier prior to its rupture, with a sampling rate of 100 Hz. Unfortunately, the recorder failed on 21 March, before the first break-off event, because of battery problems. A first seismic analysis of these measurements was presented by Reference Faillettaz, Pralong, Funk and DeichmannFaillettaz and others (2008).
Concurrently with the seismic measurements, we performed a careful analysis of the surface displacements of the glacier (Fig. 2). The measurement equipment consisted of a total station (Leica theodolite TM1800 combined with a DI3000S Distometer) installed at a fixed position above Randa on the other side of the valley, and seven reflectors mounted on stakes drilled into the unstable ice mass. A reference reflector was installed on a rock for correction of the measurements because of broad variations in meteorological conditions. This fully autonomous apparatus performed measurements every 2 hours. The motion of the reflectors (Fig. 1; Reference Faillettaz, Pralong, Funk and DeichmannFaillettaz and others, 2008) could be monitored only when the visibility conditions were good.
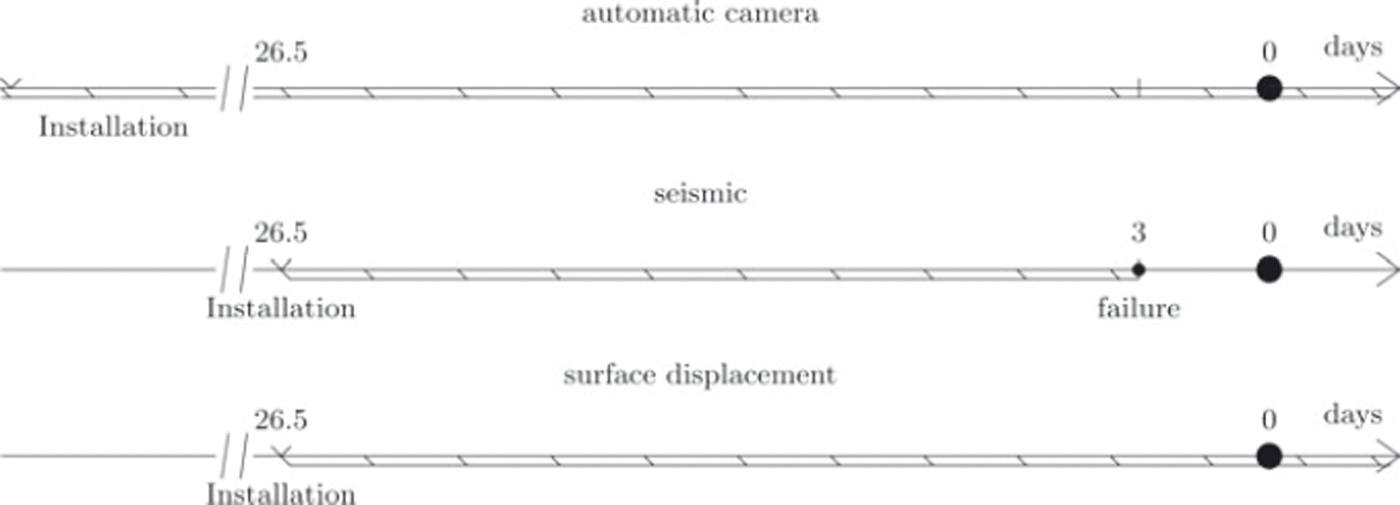
Fig. 2. Timeline of monitoring. Time 0 corresponds to the occurrence of the first break-off on 24 March 2005 (after 26.5 days of monitoring) with an estimated volume of ∼120 000 m3.
Analytical methods
Icequake detection
We identified seismic events both visually and using an automatic earthquake detection method based on the ratio of the root mean square (rms) between the short-term average (STA) window and the long-term average (LTA) window. The detection of events was performed in the following way. First, we evaluated the rms of two concurrent time windows. The rms values over the previous 800 ms LTA window and the previous 80 ms STA window were calculated and compared. When the ratio, γ = STA/LTA, exceeded a given threshold (taken here equal to 3), an event was detected and retained (Reference AllenAllen, 1978; Reference Walter, Deichmann and FunkWalter and others, 2008). The catalogues using visual or automated detection are compatible with each other and give a total number of 1731 icequakes during the monitoring period.
Icequake characterization
For deeper analysis and to allow comparison of the detected icequakes, their sizes were evaluated. Seismic event sizes were estimated based on their signal energies as defined for a digitalized signal by Reference Amitrano, Grasso and SenfauteAmitrano and others (2005):
where A is the signal amplitude and δt is the sampling period. We manually selected the beginning and end of each of the 1731 signals and performed the discrete summation for the evaluated duration of each event.
Finally, these methods enabled a catalogue of events to be obtained, containing time of occurrence and the energy for each detected icequake. It was then possible to analyze this catalogue with statistical tools and methods developed for earthquake study.
Results
Signal characteristics
The data show a high seismic emissivity from the hanging glacier during the time-span of our observations. In the case of the Weisshorn hanging glacier only, seismic events with short and impulsive signals and similar spectra were observed (Fig. 3), with dominant power contained in the 10–30 Hz frequency band. This observation is consistent with previous results (Reference Neave and SavageNeave and Savage, 1970; Reference Deichmann, Ansorge, Scherbaum, Aschwanden, Bernardi and GudmundssonDeichmann and others, 2000; Reference O’Neel, Marshall, McNamara and PfefferO’Neel and others, 2007; Reference Roux, Marsan, Metaxian, O’Brien and MoreauRoux and others, 2008). This result is not surprising, as no serac falls could be observed during the time-span of our observations (based on daily photographs). Since the sensor was very close to the sources, attenuation was low. The proximity of the source (<300 m) gave rise to difficulties in distinguishing P and S waves.

Fig. 3. Unfiltered velocity seismogram of a typical event (maximum amplitude 2.5 μm s−1) and its corresponding normalized power spectrum density (right).
As the geophone was situated above the upper crevasse separating the active from the stable zone, compressive seismic waves (primary waves) were perturbed by the discontinuity of the material and therefore were less likely to be observed.
Figure 4 shows the number of detected events per hour during the 25 day period of ice destabilization. An acceleration of the seismic activity was detected 1 week before the first break-off (i.e. 2 weeks before the main break-off).

Fig. 4. Number of detected icequakes per hour (black bars) as a function of time. The smoothed number of icequakes per hour, shown as the light-gray curve, was obtained by averaging in a sliding window of 24 hours.
Size–frequency distribution of icequake energies
Analogous to the complementary cumulative distribution function, which denotes the probability that the variable considered takes a value greater than a given value, we calculated the complementary cumulative size–frequency (also called ‘survival’) distribution (CSFD) of the icequake energy before the break-off. In our case, the CSFD indicates the probability that the energy of an icequake will take a value greater than a given value.
In order to study the temporal variation of the CSFD, we used a moving window of 200 events with a 20-event shift between successive windows. We analyzed the event size distribution corresponding to each window (Fig. 5, top, shows three typical windows). The exponent, β (Fig. 5, bottom), was estimated using the maximum-likelihood fitting method with goodness-of-fit tests based on the Smirnov test (often improperly known as the Kolmogorov–Smirnov test; see, e.g., Reference Clauset, Shalizi and NewmanClauset and others, 2009, for a review of practical issues and empirical analyses). We used this statistical test to obtain reliable results given the low number of samples in each window. For each exponent, we used a goodnessof-fit test, which generates a p-value that quantifies the plausibility of the power-law hypothesis. The purpose of this test is to sample many synthetic datasets from a true power-law distribution, to determine how far they fluctuate from the power law and to compare the results with similar measurements of the empirical data. The quantification of the distance between two distributions was made using the Smirnov statistics. The p-value is defined as being the fraction of the synthetic distances that are larger than the empirical distance. If p is not too small (i.e. p > 0.1), the difference between the empirical and the synthetic data could be attributed to statistical fluctuations alone; if p < 0.1 (0.05) the fit is poor and the model is not appropriate at the 90% (95%) confidence level. By applying the p-test to our data, we obtained p-values for each time window; the p-values greater than 0.2 are shown by empty symbols in Figure 5. This corresponds to the time windows for which we cannot reject the hypothesis that the CSFD was indeed generated from a power-law distribution.

Fig. 5. (a) The complementary cumulative size–frequency distribution (CSFD), Pr(>E) of icequake energies, E, obtained in three windows of 200 events each, corresponding to the period indicated in the panels. (b) The evolution of the exponent β of the power law fitting the CSFD obtained in running windows of 200 events. β was estimated using the maximum-likelihood method. The thin curve gives the duration of the sliding window of 200 events, corresponding to the scale on the right. The vertical bars indicate the errors given by the maximum-likelihood method. Empty symbols indicate those fits whose p-value is >0.2, i.e. for which power-law behavior is plausible. The vertical gray dotted lines indicate the transition between the different regimes (1, 2 and 3).
Three different behaviors were observed in succession:
-
1. For the windows located near the beginning of our measurements (up to t = 15 days), the CSFD was well described by a power-law distribution over at least three orders of magnitude (upper left panel of Fig. 5), indicating a scale invariance of the acoustic emissions.
-
2. From t = 15 to 5 days, the exponent β exhibited a rapid shift, suggesting a change in behavior of the damage process developing in the ice mass. Low p-values in this period indicate that the power-law behavior does not offer a plausible fit.
-
3. For the time windows near the end of our observation period (after t = 5 days), the CSFD recovered a power-law behavior, with a high β value, with a shoulder at the tail of the distribution (upper right panel of Fig. 5).
Waiting-time distribution and accelerating rate of icequakes
The time evolution of the rate of icequakes is well captured by the inverse of the mean time lag between two consecutive icequakes. Figure 6 shows this inverse mean time lag (which can be associated with a mean frequency of icequake events, i.e. the seismic activity) in a moving window containing 100 events as a function of the time of the last point of the window. This is the smallest window where the acceleration of icequake activity prior to the break-off is robustly observed. One can clearly observe a general acceleration of icequake activity ∼1 week before the break-off of the glacier.

Fig. 6. Plot of the inverse of the waiting time between successive icequakes (noisy gray curve) and of the oscillatory part of the evolution of the surface velocity (smooth dark oscillatory curve). Inset: surface velocity as a function of time to the first break-off.
We performed the same statistical analysis as for icequake activity on the waiting-time distribution between icequakes (Fig. 7). A change in the waiting-time distribution occurs as global rupture is approached. It appears this distribution is initially well described by a power-law distribution, indicating a temporal correlation between the icequakes. A few days before the glacier break-off, the waiting-time distribution shifted to an exponential distribution, indicating a loss of temporal correlation between the icequakes.

Fig. 7. Complementary waiting-time distribution, Pr(X > x), for the 100 events before and after the transition (≃5.2 days) between stable and unstable regimes. τ is the waiting time between two icequakes, (τ) is the mean of all the waiting times considered. The data for t ≤ 5.2 days can be well fitted by the exponential function: p(x) ∼ a exp(bx) with a = 110 and b = −0.93. For t > 5.2 days, the distribution of waiting times was compatible with a power law: p(x) ∼ x−α for x > x min with α = 1.5 and x min = 0.058.
Surface displacements
Thanks to very accurate surface displacement measurements (precision better than <1 cm), Reference Faillettaz, Pralong, Funk and DeichmannFaillettaz and others (2008) could demonstrate that surface motion increases with time according to a power-law acceleration before the break-off of this hanging glacier. Moreover, this acceleration was accompanied by oscillations which increased logarithmically in frequency as the time of failure approached (referred to as log-periodic oscillations). Such behavior can be found in other scientific fields, such as earthquake monitoring (Reference Sornette and SammisSornette and Sammis, 1995; Reference SornetteSornette, 2006), rupture in composite materials (Reference Anifrani, Le Floc’h, Sornette and SouillardAnifrani and others, 1995), finance and population dynamics (Reference Ide and SornetteIde and Sornette, 2002). Log-periodicity, i.e. periodicity in the logarithm of the timeto-rupture, t c − t, (where rupture occurs at time t c) is the empirical signature of the symmetry of discrete scale invariance. In other words, it means that the observable is self-similar to itself only under integer powers of a fundamental scaling ratio, λ, of timescales (see review and details by Reference SornetteSornette, 1998).
This log-periodic behavior can be shown by an equation describing the surface displacement as a function of time:

Here s 0 is a constant, t c is the critical time at which the global collapse is expected, m < 1 is the power-law exponent quantifying the acceleration, a is a constant, C is the relative amplitude of the oscillations with respect to the overall power-law acceleration and D is the phase of the log-periodic oscillation.
Interpretation and Discussion
Size–frequency distributions of icequake energy
As described above, three different regimes can be identified during the maturation of the rupture event:
-
1. The size–frequency distribution of icequake energy exhibits a power-law behavior, indicating a scale invariance of the acoustic emissions, similar to that characterizing earthquakes. For earthquakes, the corresponding Gutenberg–Richter law describes one of the most ubiquitous statistical regularities observed (e.g. Reference Pisarenko and SornettePisarenko and Sornette, 2003, and references therein). It reads
(3)
where N(>E) is the number of events with an energy greater than E and β is the Gutenberg–Richter exponent found empirically to be close to 2/3 for shallow earthquakes (depths <70 km) in subduction and transform-fault zones. Up to t = 15 days, the exponent β is found to be compatible with the earthquake value, β = 0.65 ± 0.1. This behavior can be associated with a stable critical regime, in accordance with the critical behavior of rupture found in sufficiently heterogeneous media (Reference Johansen and SornetteJohansen and Sornette, 2000), similar to critical phase transitions (from diffuse damage to crack nucleation). As this non-equilibrium system exhibits a kind of dynamic criticality without tuning any control parameter, this regime could be associated with a self-organized critical (SOC) behavior. Reference JensenJensen (1998), Reference TurcotteTurcotte (1999) and Reference SornetteSornette (2006) give introductions and detailed presentations of the concepts and models of self-organized criticality. The first stable regime fulfills the SOC characteristics: (a power-law distributions, such as those observed in this regime, (b) a constant driving stress, (c) a threshold dynamics and (d) a very large number of interacting local entities (here, the microcracks). In other words, in such a regime, the glacier has time to adapt to the new state induced by the rupture maturation process.
-
2. In this transitional regime the glacier can no longer adapt itself to the changes induced by rupture maturation, and the CSFD of icequakes is no longer a power law. Large ‘characteristic events’ can be seen in the tail of the distribution, and we interpret this as the nucleation of the incipient rupture.
-
3. The size–frequency distribution of icequake energy exhibits a power-law behavior with a larger value of β and the appearance of characteristic events. Reference Pisarenko and SornettePisarenko and Sornette (2003) have associated a change in β with a change in the rupture process. They proposed the following explanation of these two regimes: First, large β values are found in the distribution of acoustic-emission energies recorded for heterogeneous materials brought to rupture, for which damage occurs mainly in the form of weak shear zones and open cracks. In other words, large β are an indication of an open-crack mode of damage. Second, when damage develops in the form of ‘dislocations’ or mode II cracks, with slip mode of failure and with healing, the exponent β is found to be <1. This suggests that the low value of β ≃ 2/3 found up to 2 weeks before rupture is associated with a stable, slow and diffuse ‘dislocation-like’ damage process. In the subsequent days, the increase in β, together with the developing shoulder at high icequake energies, can be interpreted as revealing a transition to a mode of damage controlled more and more by crack openings and their coalescence prior to the incipient rupture. The tail of the distribution develops a strong shoulder, indicating a change in the damage evolution process. The clear deficit of icequakes with low energies and the excess of large ‘characteristic’ events (events with high energy) is fully compatible with the evolution of the second regime dominated by crack-like events which, by their proliferation and fusion, progressively nucleate the formation of the runaway macrocrack responsible for the final avalanche associated with a rather clean crack-like rupture, as shown in Figure 1. Moreover, as coupling between cracks increases, and heterogeneity decreases, the power law develops a shoulder, corresponding to a different regime of global rupture (Reference SornetteSornette, 2009).
Seismic activity
Acoustic emissions were also observed experimentally in heterogeneous materials brought to rupture and were found to exhibit clear acceleration, in agreement with a power-law divergence expected from critical point theory (Reference Johansen and SornetteJohansen and Sornette, 2000). In a nutshell, critical point theory views the global rupture of a system as the result of a progressive process of defects. The global rupture corresponds to a ‘bifurcation’ (also known as ‘phase transition’, ‘catastrophe’ or ‘tipping point’), resulting from the collective organization of defects that interact to prepare the global transition, i.e. the rupture (Reference Sornette and SornetteSornette and Sornette, 1990; Reference Sornette and VannesteSornette and Vanneste, 1990; Reference Anifrani, Le Floc’h, Sornette and SouillardAnifrani and others, 1995; Reference Andersen, Sornette and LeungAndersen and others, 1997; Reference Sornette and AndersenSornette and Andersen, 1998; Reference SornetteSammis and Sornette, 2002). The concept of critical rupture suggests that global ruptures are preceded by specific precursors that make them predictable in a probabilistic way (Reference Anifrani, Le Floc’h, Sornette and SouillardAnifrani and others, 1995; Reference SornetteSornette, 2002).
Our results also support this picture as they clearly indicate a general acceleration of icequake activity (i.e. acoustic emissions within the hanging glacier) ∼1 week before the break-off event. Recent studies in material science also show a clear transition to the tertiary creep regime with an acceleration in the rate of acoustic emissions (Reference Nechad, Helmstetter, El Guerjouma and SornetteNechad and others, 2005a, Reference Nechad, Helmstetter, El Guerjouma and Sornetteb, and references therein).
Comparison between icequake activity and surface displacement
The surface motion acceleration described by Reference Faillettaz, Pralong, Funk and DeichmannFaillettaz and others (2008) was accompanied by oscillations which increased logarithmically in frequency as the time of failure approached (referred to as ‘log-periodic oscillations’). The origin of such oscillations is not yet fully understood, but dynamic crack interactions have been suggested as a possible mechanism (Reference Saleur, Sammis and SornetteSaleur and others, 1996; Reference Huang, Ouillon, Saleur and SornetteHuang and others, 1997; Reference Ide and SornetteIde and Sornette, 2002).
The discrete hierarchy of the organization of damage revealed by the log-periodic oscillations (Reference Faillettaz, Pralong, Funk and DeichmannFaillettaz and others, 2008) should somehow influence the seismic activity of the glacier during the maturation of the rupture process. Figure 6 shows the comparison between the oscillatory part of the velocity (time derivative of the surface displacements which follow a log-periodic power law) and the inverse of the waiting time between successive icequakes.
It appears that these two metrics exhibit a significant correlation (r 2 = 0.65). This result suggests that the seismic activity is not correlated with the global power-law acceleration of the glacier during the rupture maturation (where r 2 = 0.29) but, rather, with its superimposed oscillations. It is the more jerky motions around the overall accelerations that are responsible for detectable seismic activity (Reference Johansen and SornetteJohansen and Sornette, 1999) corresponding to crack growth and coalescence events within the glacier.
Waiting-time distribution
The waiting-time distribution was seen at first to follow a power law, and then shifted to an exponential distribution (Fig. 7). This result is in accordance with the previous physical interpretation of crack coalescence (Reference Huang, Ouillon, Saleur and SornetteHuang and others, 1997). The random activation of different damage clusters when approaching global failure causes a transient loss of the temporal correlation of the individual fracture events (Reference Kuksenko, Tomilin and ChmelKuksenko and others, 2005). This effect confirms the existence of a hierarchical structure of the fracture process in the glacier. We tentatively attribute this change of the distribution of waiting times from power-law to exponential to the transition from a diffuse to a cluster damage organization.
In contrast to the difficulties in ascertaining the existence of an accelerating moment release (i.e. an intensifying of the seismic energy released in the surrounding regions of a fault) upon the approach to a large earthquake (Reference Hardebeck, Felzer and MichaelHardebeck and others, 2008), the four metrics that we applied to our glacier data support the existence, in this case, of accelerated deformation and damage evolution occurring in the last few days before the break-off.
Evolution of failure processes leading to the break-off event
It is now possible to draw the following picture of the evolution of the failure processes leading to the break-off event:
-
1. From the beginning of our measurements to 15 days before the break-off event: In this regime, seismic activity is more or less constant, the size–frequency distribution of icequake energies is described by a power-law behavior and the waiting time distribution also follows a power law. This behavior could be related to a self-organizing regime, where diffuse damage accumulates within the glacier, with a proliferation of dislocation-like defects. In other words, the glacier has time to adapt to the deformation and damage maturation process.
-
2. From 15 to 5 days before the break-off event: Seismic activity is slightly decaying, the size–frequency distribution is no longer power-law, the waiting-time distribution is power-law and the glacier is decelerating relative to the previous phase. This is a transitional regime; the damage process goes on, microcracks grow and start merging in a homogeneous way. Log-periodic oscillations appear and reveal the hierarchical structure of the fracture process under development. In such a regime, screening and locking effects are likely to appear (Reference Huang, Ouillon, Saleur and SornetteHuang and others, 1997), possibly explaining the slight decay of icequake activity and the relative slowdown of surface velocity.
-
3. From 5 days before the final break-off event: Seismic activity dramatically increases, the size– frequency distribution of icequake energy recovers its power-law behavior but with a different exponent, together with the appearance of some large characteristic events leading to a strong shoulder in the distribution. The waiting-time distribution exhibits a shift from a power-law to an exponential distribution. The system enters a catastrophic regime where damage clusters are randomly activated. Damage clusters interact and merge with a preferential direction (i.e. preparing the final rupture pattern), in contrast to the previous regime. The largest scale of the hierarchical structure of the fracture process is activated (resulting in characteristic events).
Summary and Perspectives
We have obtained a unique dataset of icequakes recorded in the immediate vicinity of a hanging glacier over 25 days prior to its rupture. Although the seismic measurement records unfortunately ceased 3 days before the first break-off and 10 days before the larger subsequent one, we were able to obtain a coherent quantitative picture of the damage evolution process developing before the glacier break-off. By analyzing the size–frequency distribution of icequake energies and the inverse of the waiting time between successive icequakes, we identified three regimes in the evolution of the failure processes leading to the break-off event:
-
1. A stable phase related to a self-organizing regime, where diffuse damage accumulates within the glacier, with a proliferation of dislocation-like defects. In other words, the glacier has time to adapt to the deformation and damage maturation process.
-
2. A transitional phase where the damage process goes on, microcracks grow and start merging in a homogeneous way. Log-periodic oscillations appear and reveal the hierarchical structure of the fracture process under development.
-
3. A catastrophic regime where damage clusters are randomly activated. Damage clusters interact and merge with a preferential direction (i.e. preparing the final rupture pattern), in contrast to the previous regime. The largest scale of the hierarchical structure of the fracture process is activated (resulting in characteristic events).
Moreover, four types of precursory signals of the imminent catastrophic rupture were highlighted:
A clear increase in icequake activity within the glacier (measured as the inverse of the waiting time between successive icequakes) starting ∼6 days before the first break-off.
A two-step evolution of the size–frequency distribution of icequake energies, characterizing a first transition to crack-like dominated damage followed by a second transition, in which large characteristic cracks prepared the nucleation of the runaway rupture.
The acceleration of the rate of icequake occurrence combined with a change in the distribution of waiting times between icequakes, which is typical of the hierarchical cascade of rupture instabilities found in earlier studies on the acoustic emissions associated with the failure of heterogeneous materials (Reference Huang, Ouillon, Saleur and SornetteHuang and others, 1997).
A clear correlation between the seismic activity and the oscillatory part of the surface velocity evolution prior to the first break-off event.
By combining the analysis of surface motion with log-periodic oscillations and icequake activity during the rupture maturation process, the prediction of the final break-off time can be significantly improved.
Provided technical solutions can be found to ensure continuous icequake recordings in the difficult high-altitude mountain conditions, our results clear the path for real-time diagnostics of impending glacier failure. The next steps towards this goal include (1) developing automatic seismic data processing in real time (which includes the automatic detection of icequakes and the determination of their energy), (2) processing these data with the statistical tools developed here and (3) performing systematic reliability tests to access the rate of false alarms (false positives or errors of type I) versus missed events (false negatives or errors of type II). Step (3) is necessary for an informed cost– benefit analysis of the societal and economic impacts of the proposed real-time forecast methodology.
Acknowledgements
The Institute of Geophysics, ETH Zürich, is gratefully acknowledged for allowing us to use their instruments. Thanks are extended to F. Walter for fruitful discussions. P. Winberry, an anonymous referee and T. Scambos contributed substantially to improvements made to the manuscript. We are also grateful to C. Wuilloud (natural hazards, Valais) for logistic and financial support.









