Introduction
Ice masses in polar regions show various deformation characteristics depending on stress, temperature, hydrostatic pressure and other parameters (Reference Budd and JackaBudd and Jacka, 1989). Deformation of ice in glaciers and ice sheets is controlled mainly by dislocation activity in ice crystals (Reference Schulson and DuvalSchulson and Duval, 2009). Thus, the formation, accumulation and recovery of dislocations determine the strength of the material. Accumulated in subgrain boundaries as arrays, dislocations cause lattice misorientations (Reference Weertman and WeertmanWeertman and Weertman, 1992; Reference Hull and BaconHull and Bacon, 2001). Characteristics of the probable dislocation types involved in this misorientation can be determined if full crystal orientation measurements are available (Reference Prior, Wheeler, Peruzzo, Spiess and StoreyPrior and others, 2002). Since different subgrain boundary types, classified by shape and c-axis orientations, have been observed as major microstructure features during creep tests on polar and artificial ice (Reference Hamann, Weikusat, Azuma and KipfstuhlHamann and others, 2007; Reference Weikusat, Kipfstuhl, Faria, Azuma and MiyamotoWeikusat, 2009), we can improve our knowledge of dislocation activity using high-accuracy, full crystal orientation analysis on the subgrain scale. To determine microstructural features of natural ice-core samples, the measurement device must be suitable for ice crystals of a few millimetres to several centimetres in diameter.
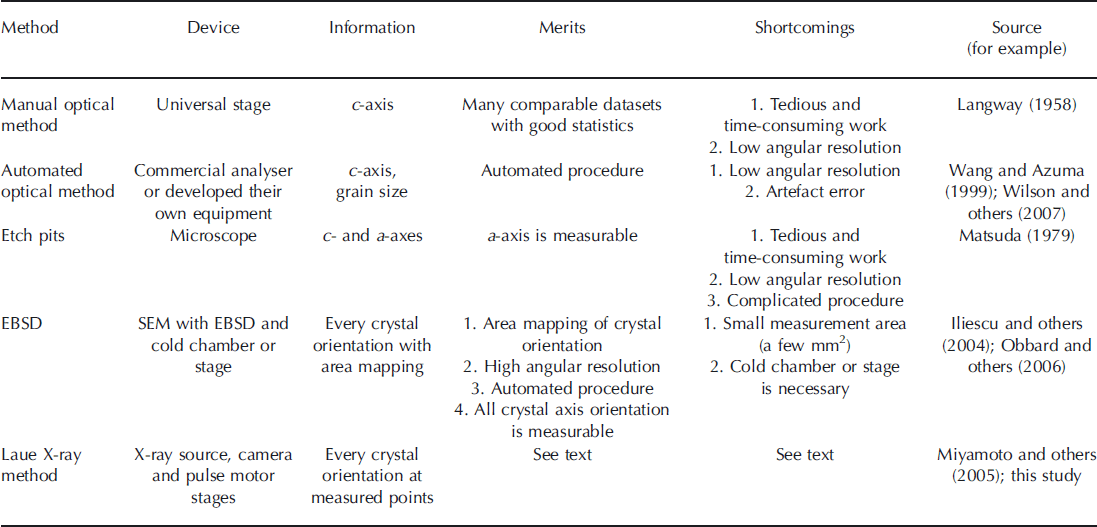
Three predominant techniques are employed to measure orientation of ice crystals: optical observation, etch-pit observation and electron backscatter diffraction.
The most traditional course is an optical approach using a Rigsby stage, a universal stage with four rotation axes. This method utilizes the birefringence and extinction of the optically uniaxial ice crystal between crossed polarizers (Reference RigsbyRigsby, 1951; Reference LangwayLangway, 1958; Reference KambKamb, 1962). Because a typical ice crystal is hexagonal, with only one optical axis, the only measurable orientation is the c-axis. Although this method requires elaborate and time-consuming measurement procedures, it has a major advantage: abundant previous studies are available for data comparison using this method (e.g. Reference RigsbyRigsby, 1951; Reference Gow and WilliamsonGow and Williamson, 1976; Reference Herron and LangwayHerron and Langway, 1982; Reference Azuma and HigashiAzuma and Higashi, 1985; Reference Alley, Gow and MeeseAlley and others, 1995). Thus fabric patterns (e.g. single-maximums or girdles) exhibited by different ice-core samples are comparable even if measurement methods are different.
Automated devices also using the principles of the optical extinction method have become available since the late 1990s (Reference Wang and AzumaWang and Azuma, 1999; Reference Wilen, DiPrinzio, Alley and AzumaWilen and others, 2003; Reference Wilson, Russell-Head, Kunze and ViolaWilson and others, 2007) and are now commonly used in ice-core studies. The chief merits of these analysers are automation and speed: each thin-section sample takes just a few tens of minutes to process. However, automated techniques have a low angular resolution (∼5°), and we know empirically that large artefact errors occur, possibly due to illumination problems (M. Montagnat and others, unpublished information). Furthermore, the measured angles deviate from the true angles due to the large differences between the refractive indices of air and ice if c-axes are aligned with high angles with respect to the thin section (Reference LangwayLangway, 1958).
The second major method of crystal orientation measurement is by observation, under a microscope, of etch pits, which are generated by the application of a polyvinyl formal solution (Reference HiguchiHiguchi, 1958; Reference MatsudaMatsuda, 1979). As the etch pits form shapes of a section cut from a hexagonal column, the full crystal orientation can be determined. This method also involves laborious, time-consuming work in a cold laboratory. Furthermore, the results depend on the skill of the operator, and only low angle resolutions (>5°) can be obtained. In addition, a reliable method to generate a measurable etch pit on the ice surface is difficult to establish because the density of the polyvinyl formal solution, sublimation time, temperature and other factors strongly influence the quality of etch-pit shape. Additionally, the shape of the etch pits changes every moment (personal communication from N. Azuma, 2010). The advantage of the etch-pit method is that we can measure c- and a-axes orientations with high spatial resolution (several tenths of a micrometre), strongly depending on the visibility of the etch pit and thus the operator’s skill.
The third method for crystal orientation measurements is electron backscatter diffraction (EBSD) used as an add-on package with a scanning electron microscope (SEM; Reference Randle and EnglerRandle and Engler, 2000). This is a long-established method in metallurgy, material science and geology (Reference HumphreysHumphreys, 2001; Reference Pennock and DruryPennock and Drury, 2005) but is rarely used for ice. EBSD enables area mapping of crystal orientation with high spatial resolution, but the measurable area for mapping is normally small (a few mm2) due to the small sample size of a few cm2 (Reference Iliescu, Baker and ChangIliescu and others, 2004; Reference Obbard, Baker and SiegObbard and others, 2006; Reference Piazolo, Montagnat and BlackfordPiazolo and others, 2008). This small sample size is problematic for the localization of relevant structures since natural polar ice-core samples contain large grains and a heterogeneous distribution of microstructure features. Moreover, an expensive and complex measurement set-up is required to measure ice-core samples, including an SEM equipped with an EBSD detector and cryogenic thermostat chamber or stage. The measurement conditions (e.g. the complicated sublimation and condensation dynamics in a vacuum) must also be controlled (Reference Iliescu, Baker and ChangIliescu and others, 2004; Reference Weikusat, de Winter, Pennock, Hayles, Schneijdenberg and DruryWeikusat and others, in press). Advantages of this method are full automation and the possibility of detecting all crystal axis orientations with high accuracy.
All three methods described above have recently been used in ice-core studies. Currently, the most common technique is the automated optical method because no special skills are required to measure crystal orientation, and advanced commercial devices are available.
X-ray diffraction was used by M. von Laue in 1912–13 to prove the periodic lattice structure of crystals and the electromagnetic character of X-radiation (Reference EwaldEwald, 1962). This method, named after Laue, is now primarily used to measure single crystal orientations and is traditional for crystal orientation measurements; the approach is still common in material sciences. In our study, we adapt this method, for the first time, to polycrystalline samples from an ice sheet. Merits, shortcomings and sources are summarized in Table 1.
Table 1. Comparison of crystal orientation measurement methods for ice samples
Experimental Methods
The experimental arrangement for our full crystal orientation fabric analyser is shown in Figure 1a and b. The specially designed X-Yaxes pulse motor stages, manufactured by Chuo Precision Industrial Co., Ltd (positioning accuracy 50 μm; unidirectional repeatability ±5 μm), the charge-coupled device (CCD) camera, the light-emitting diode (LED) light source and the X-ray camera (Rad-icon Shad-o-Box 1024) with X-ray source device (Rigaku SLX-2000, 60 kV and 250 mA) were assembled to detect each crystal orientation within thin-section samples. Since all devices were installed in a cold laboratory at −15°C, a cold chamber or cryo-stage was not required. For ice-core studies, we prepared standard thin sections of ∼100 mm × 100 mm with a thickness of <0.5 mm for crystallographic analyses. Sections this large are necessary to observe a few hundred grains because of the large grain sizes, typically a few millimetres to a few centimetres in natural polar ice. Crystal orientations of >200 grains are required for sufficient fabric determination.
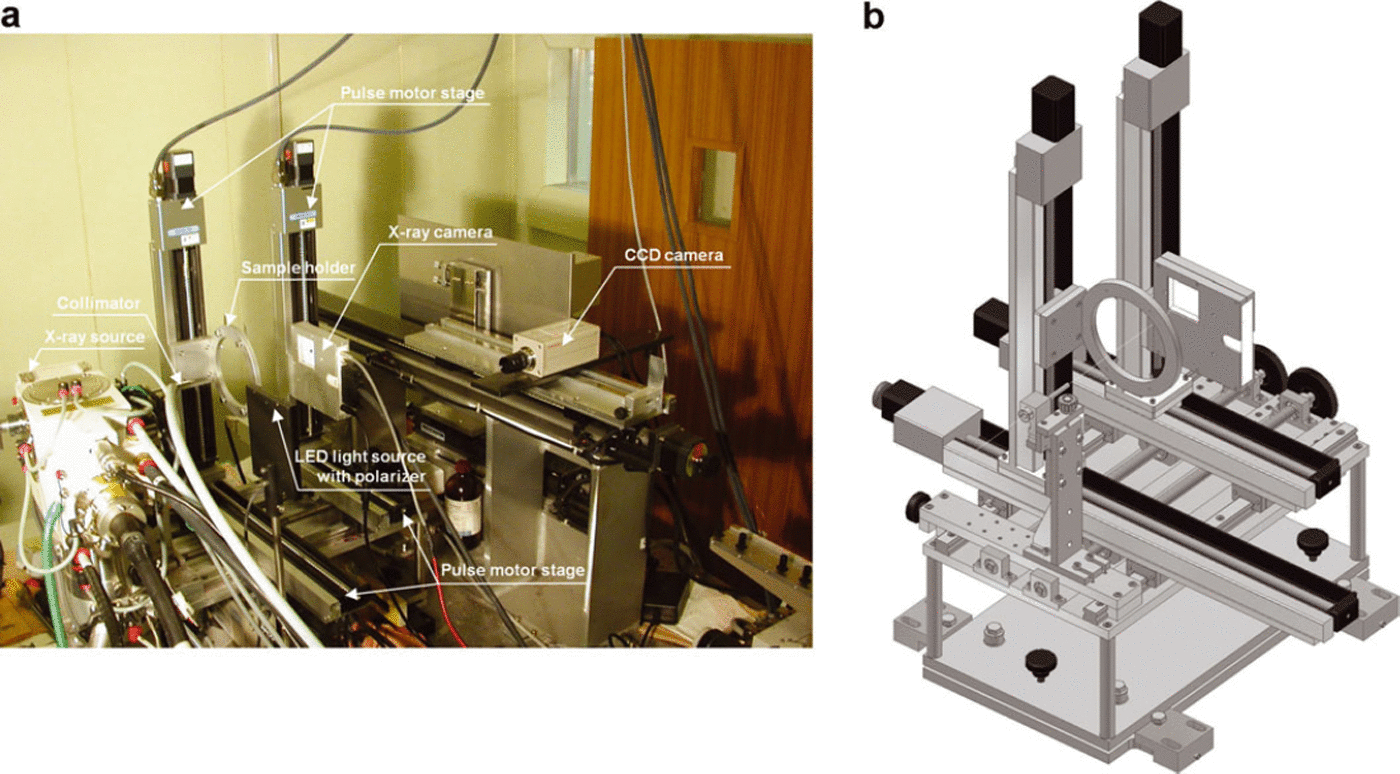
Fig. 1. (a) Photograph of entire experimental arrangement in cold laboratory. (b) Schematic of X-Y stages, collimator, sample holder and X-ray camera.
Development of a semi-automated Laue X-ray diffraction method
Using an earlier version of this device (Reference Miyamoto, Shoji, Hori, Hondoh, Clausen and WatanabeMiyamoto and others, 2005), we had already succeeded in obtaining accurate c- and a-axis orientation measurements, providing complete ice-core thin-section crystal orientation of fabrics. In our study, however, longer analysis times were required for a single grain, so it was not suitable for many measurements. In order to reduce measurement time and apply the method to microstructure studies, we aimed to automate the analysis of Laue X-ray diffraction, which is traditionally used only in single crystal analysis.
The Laue pattern digitizing and analysis software was developed in collaboration with Norm Co., Ltd, a Japanese software company that develops various X-ray analyses. However, this software is designed to analyse the orientation of single crystals and is unsuitable for the study of polycrystals. Thus, we ‘customized’ the software to the requirements of ice-core analysis. Specifically, the following changes were made so as to analyse many measurement points in a reasonable time:
-
1. The objective orientations (c-axis and three a-axes) were inputted in advance.
-
2. After each individual analysis, the c-axis and three a-axes orientations were sent to a text file.
-
3. Many minor changes, such as the Laue pattern simulation algorithm for finding a matching pattern (the solution) and the procedure cycle (opening the Laue figure, digitizing Laue spots, finding a matching pattern, displaying the result and saving the result), were implemented to reduce analysis time. With the previous software we required a long calculation time and several operator interactions when proceeding to the next operation.
The present program version is 5.1.1.
The steps in our crystal-orientation analysis are as follows:
-
1. We prepare a thin section using an X-ray transparent object slide that consists of a 2 mm thick clear acrylic resin plate. The maximum size of the thin section is ∼100 mm × 100 mm, and the thickness is <0.5 mm depending on grain size. The ice-sample thin section is covered with silicone oil and polyester film to avoid sublimation during measurement. The sample is inserted into the sample holder of the X-ray device (Fig. 2). This is the only step that had to be performed in a cold laboratory.
-
2. We decide upon a measurement position through the CCD camera with a polarizer using a stage controller. We recognize each grain on the monitor according to the grey-value differences. We fix measurement points by operating the X-Y stage using a joystick manipulator. The X-ray collimator axis and fixed point on the monitor are already linked. The measurement positions are saved as a series of X-Y coordinates in a text file. When we want to make equally spaced measurement points or grid measurement points for microstructure study or other purposes, we edit a test file that represents such coordinates or we move the X-Y stage equidistant to the stage controller. The minimum detectable grain size is ∼0.5 mm, which is larger than the collimator size; smaller grains were difficult to recognize through the CCD camera.
-
3. The actual Laue measurements, i.e. positioning on the measurement point, irradiation of X-ray and imaging of the Laue figure by the X-ray camera, are fully automated in our system.
-
4. After obtaining all Laue figures, we prepare the Laue pattern digitizer and analysis program. The objective four orientations, (001) as c-axis and
 , (110) and
, (110) and  as a-axes (Fig. 3), are inputted to the software.
as a-axes (Fig. 3), are inputted to the software. -
5. A few Laue spots from different crystal zones are digitized manually, and solution candidates for the Laue diagram are calculated by the software. If a candidate is provided, we confirm the simulated Laue pattern of the solution (Fig. 4) to reduce analysis error. The calculated orientations are sent to a result file.

Fig. 2. Photograph of sample holder with ice core, thin-section sample.
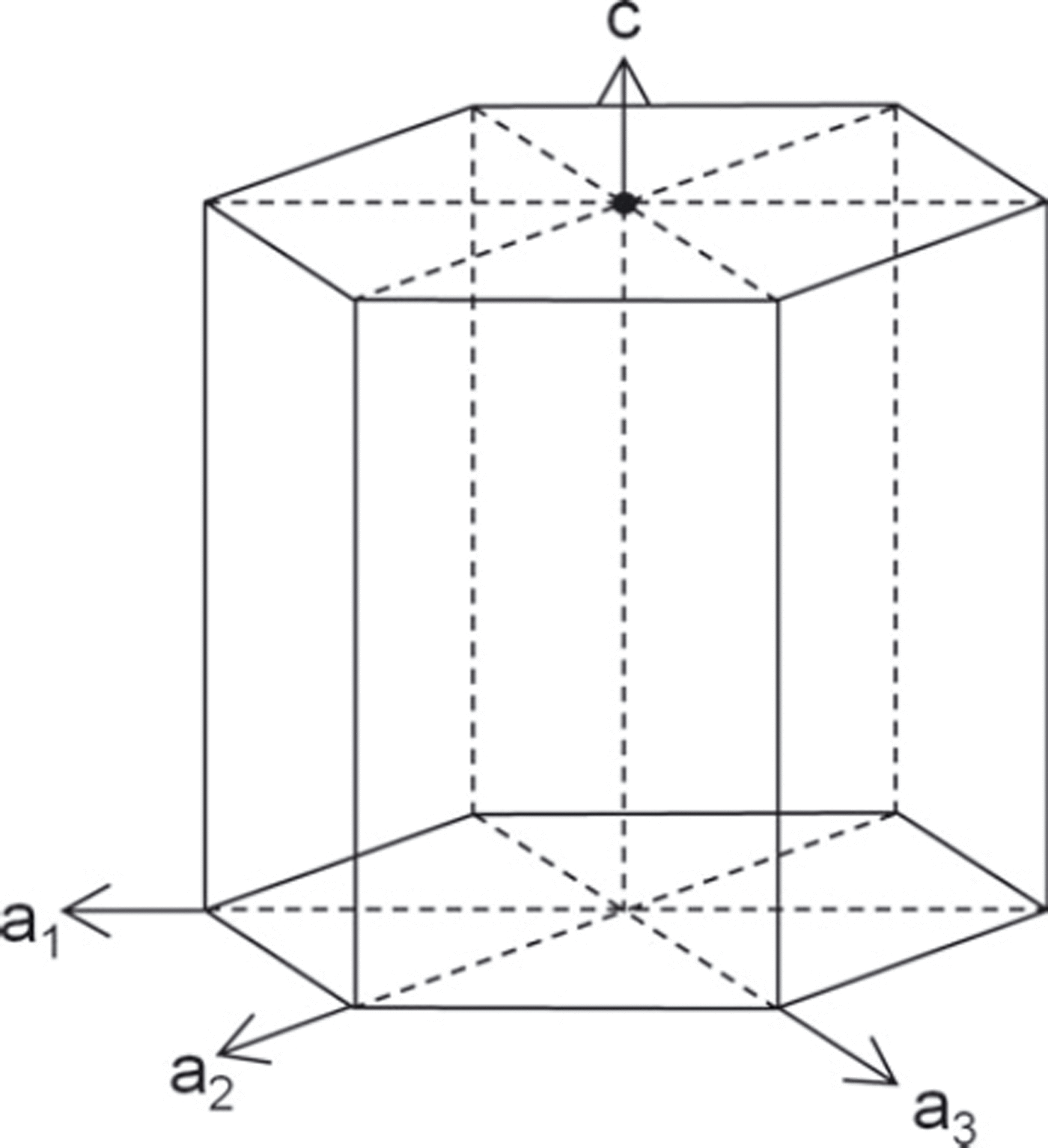
Fig. 3. Schematic diagram of measured four axes (c, a 1, a 2 and a 3) of hexagonal ice crystal.
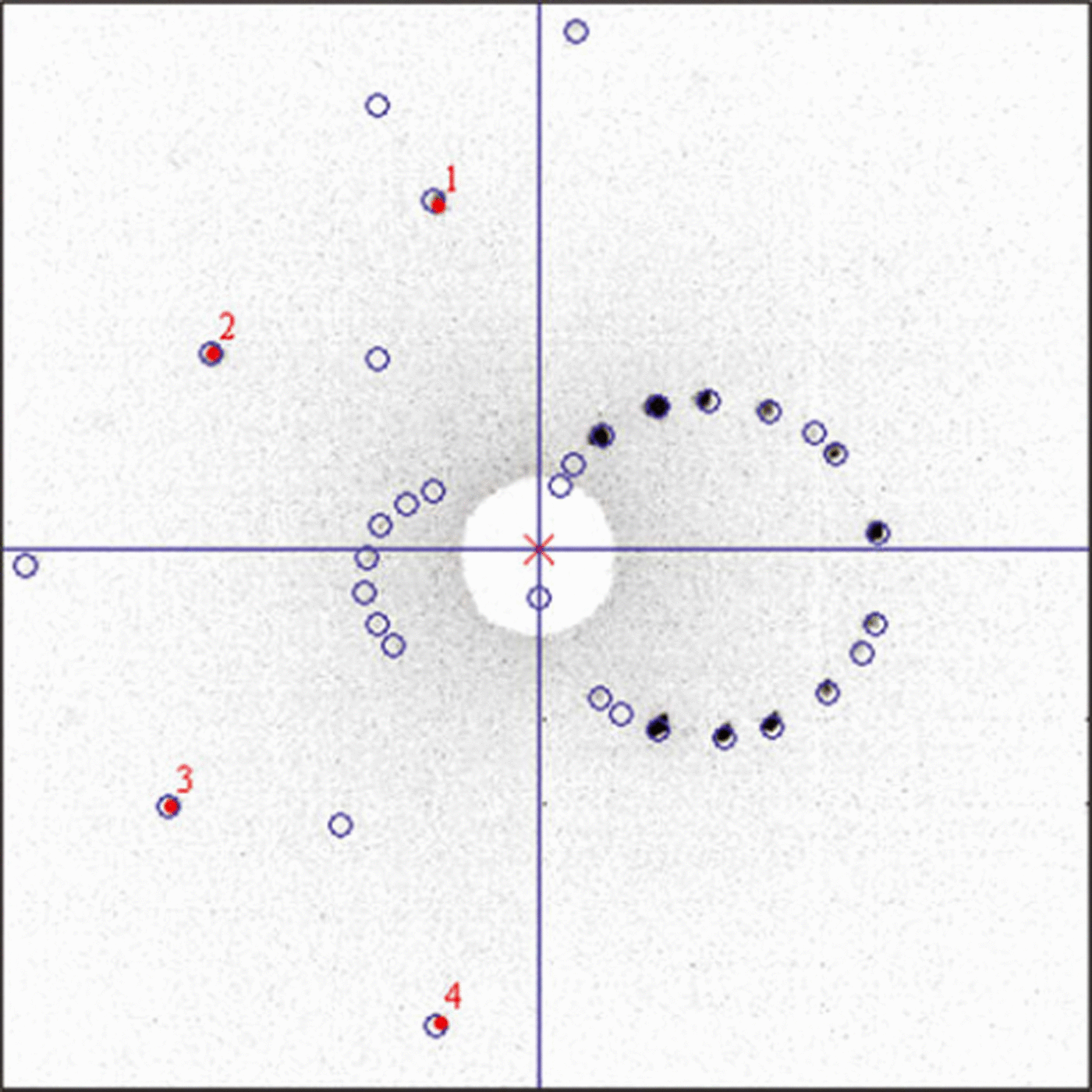
Fig. 4. Displayed Laue figure on Laue pattern digitization and analysis program. The black dots indicate original Laue pattern from X-ray camera. The four numbered red dots show digitized points just on the acquired Laue spots. The open blue circles indicate simulated Laue pattern. The comparison of simulated and measured spots enables high accuracy and accelerated measurements.
The described improvements and modifications of the system make the X-ray analyser very suitable for ice-core studies. Using this semi-automated system, we were able to analyse ∼200 measurement points every day.
Results and Discussions
Spatial resolution
As previously mentioned, we need large thin sections due to the comparatively large grain size of natural polar ice-core samples, typically greater than a few millimetres. However, since grain substructure characterization is essential to understand the dislocation dynamics, the spatial resolution is important. The diameter of the X-ray beam we set up was 0.2 mm, determined by the collimator size, which is suitable for adjusting a correlation between the X-ray power and the quality of the Laue spots figure – the sensitivity of the X-ray camera – in this setting. With the collimator size set to the smallest diameter of 0.1 mm, the diffracted X-ray power was very low in order to obtain a satisfactory Laue figure. This beam size defined the minimum spatial resolution. The positioning accuracy of the X-Y stage was one order smaller than this resolution.
For fabric determination, we chose a measuring point near the centre of each crystal and provided data as shown by Reference Miyamoto, Shoji, Hori, Hondoh, Clausen and WatanabeMiyamoto and others (2005). Small crystal-orientation changes on subgrain boundaries or continuous lattice bending was observed when we moved the pulse motor stage in >0.2 mm steps within an individual grain. Even with small crystal displacement, slight changes of spot position were detected in each Laue diagram. Such small orientation changes represent new and important microstructure information for ice-core study, especially those concerning distinct subgrain boundaries.
Angular precision and accuracy
Due to the grain boundary energies (Reference SuzukiSuzuki, 1970), subgrain misorientations are expected to be <10° as in metals (Reference Humphreys and HatherlyHumphreys and Hatherly, 2004) or even <5° as in most rock-forming minerals (Reference Passchier and TrouwPasschier and Trouw, 1996). Hence, when using Laue X-ray diffraction, the angular precision is of particular importance. The process of digitizing Laue spots is a primary factor for error generation because a slight deviation of digitizing position leads to low angle precision. For this reason, the precision was determined from repeated analyses of the same Laue figure. The standard deviation of each orientation was <0.5°. To estimate the accuracy of orientation determination, we compare it with the result of X-ray diffract meter measurement. For orientations determined by the Laue method, the desired ice-lattice plane orientations were searched using rocking curve measurements. This allowed us to seek the absolute orientation if the grain showed a perfect crystal without any disturbance such as polygonization or lattice bending. Both results showed good agreement, with some angle differences less than the standard deviation determined by the Laue measurements. The precision and accuracy with which an orientation can be absolutely determined is ∼0.5° and is affected by the digitizing of Laue spots and the crystal quality. However, the relative orientations between neighbouring measurement points are the crucial parameter when detecting and characterizing subgrain boundaries. Pre-mapping of samples using sublimation etching by microstructure mapping (Reference KipfstuhlKipfstuhl and others, 2006) gives a first impression of the crystal quality by revealing subgrain boundaries as grooves. Thus, this method enables the identification of undisturbed grains. Subsequent Laue X-ray diffraction measurements within these undisturbed grains and misorientation calculation of adjacent points reveal some noise below ∼0.5°. Possible continuous lattice bending, which does not evoke sublimation etch grooves in the undisturbed grains, can be ruled out by spatially referenced examination of misorientation data. Thus, the 0.5° data noise can be regarded as the relative angular precision. In this study, we calculated the misorientation angle of the c- and a-axes separately between neighbouring measurement points. For the a-axis measurements, we calculated the misorientation angle between each a 1 axis of neighbouring measurement points. The other two axes, a 2 and a 3, were also calculated in this way, but, since the ice crystal has six rotational symmetries about the c-axis, we had to find the a-axes combinations to minimize each of its misorientation angles.
Subgrain structure measurement
We adapted our Laue X-ray method to analyse subgrain structures within ice crystals. We performed measurements on a grid in individual ice crystals in a thin-section sample (Fig. 5). The numbers of measurement points in grains A and B, which have diameters of ∼4 mm, are 230 and 257, respectively. When grains were near-perfect crystals, Laue spots of each measurement point appeared at the same position in the Laue diagram. On the other hand, when a grain had some subgrain structures, we observed spots out of position compared with adjacent points in each Laue figure. Figure 6 shows a result of multilayered, superposed Laue figures of all measurement positions in grains A and B. The Laue spots of grain A exhibit the original shape of the X-ray beam, i.e. Laue spots appear at the same position in all Laue figures. There is a lack of crystal orientation changes within this grain. Only some noise below ∼0.5° is observed (see above). On the other hand, the Laue spots in grain B do not retain the original shape of the X-ray beam. The spot position in each Laue figure shifts slightly due to small changes in crystal orientation, indicating subgrain structures such as a subgrain boundary or continuous lattice bending.
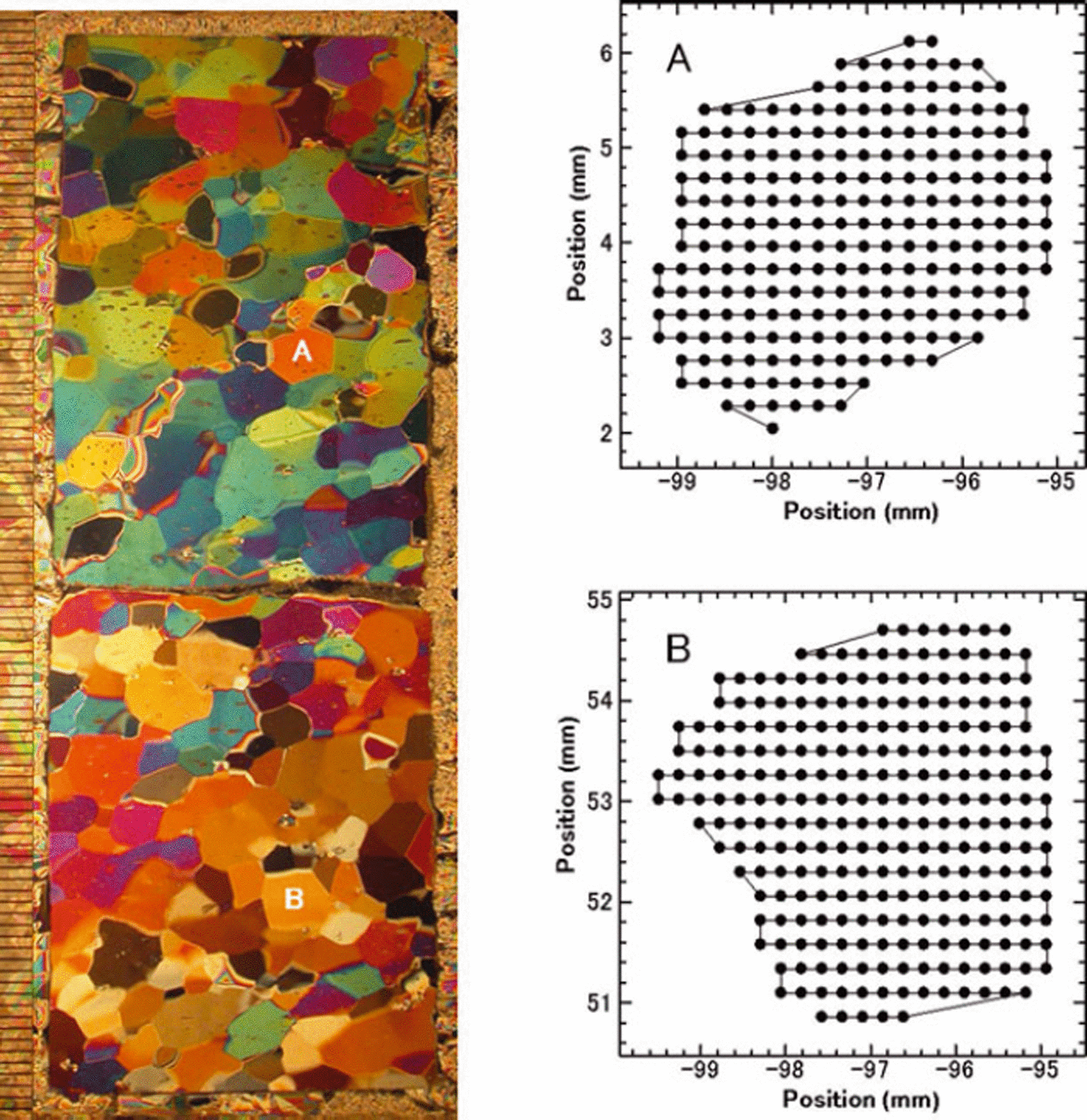
Fig. 5. Example of thin section prepared from the Greenland Icecore Project (GRIP) ice-core sample at 2702 m depth (left). This photograph was taken between crossed polarizers. The minimum scale on the left side shows 1 mm. The black dots (right-hand graphs) show measurement points within grains A and B.
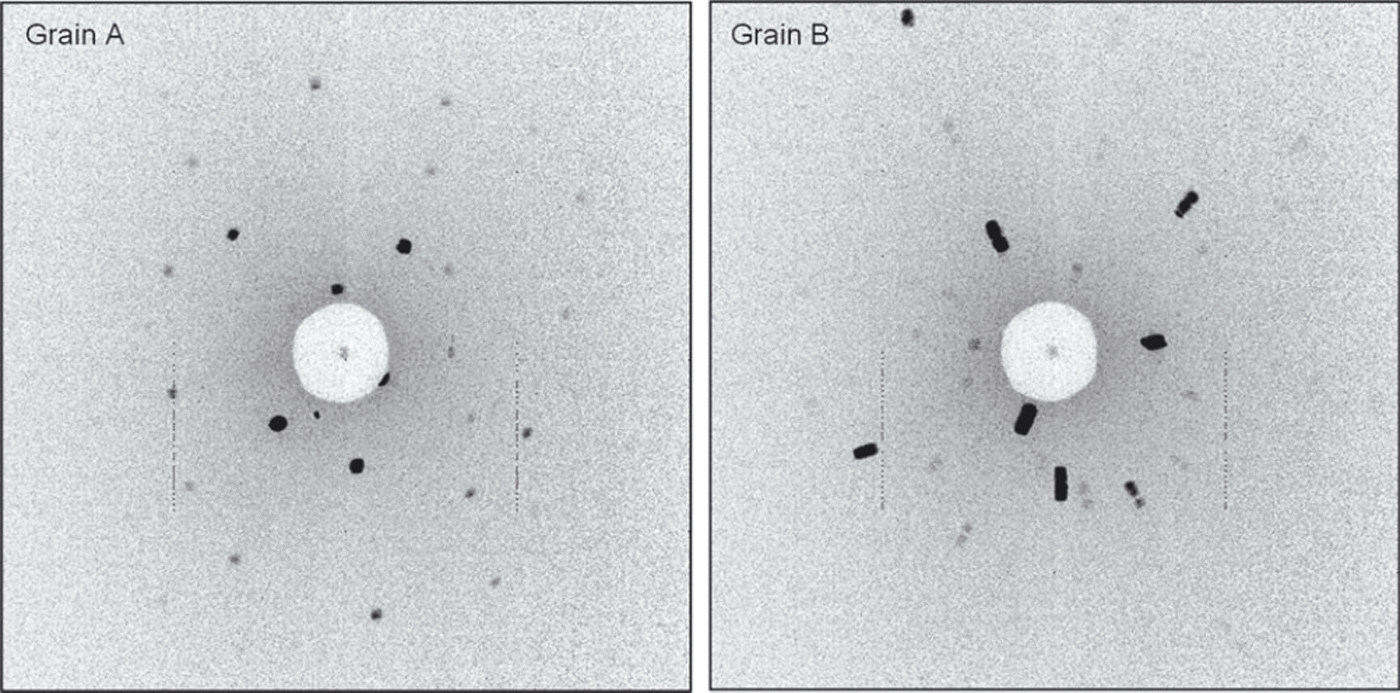
Fig. 6. Multilayered Laue figures from grains A and B. The Laue images of the 230 measurements for grain A and the 257 measurements for grain B are superposed. The stretching spots on Laue figure of grain B are evidence of Laue spots changing position with each measurement. In fact, if we observe all Laue figures of grain B as an animation movie, we readily understand the movement of the spots as the crystal lattice changes from point to point.
Figure 7 shows an example of a misorientation angle across a discrete subgrain boundary in a Dome Fuji (Antarctica) ice-core sample, which was pre-localized using an optical microscope and microstructure mapping technique (Reference KipfstuhlKipfstuhl and others, 2006). This method provides a qualitative possibility to distinguish between a distinct subgrain boundary and continuous lattice bending. We can observe subgrain boundaries as shallow sublimation grooves compared with deep, high-angle grain boundary grooves using the sublimation-etch method. The misorientation angle of the subgrain boundary in Figure 7 was determined from the analysis along a line crossing the subgrain boundary. The results indicate that the c-axis orientation hardly changes, whereas the a-axes show a misorientation angle. This crystal orientation relation across the subgrain boundary shows ∼3° of rotation around the c-axis. This novel result for natural polar ice can be produced from the complete determination of several ice crystal orientation measurements in reasonable time by our semi-automated Laue X-ray diffraction method.
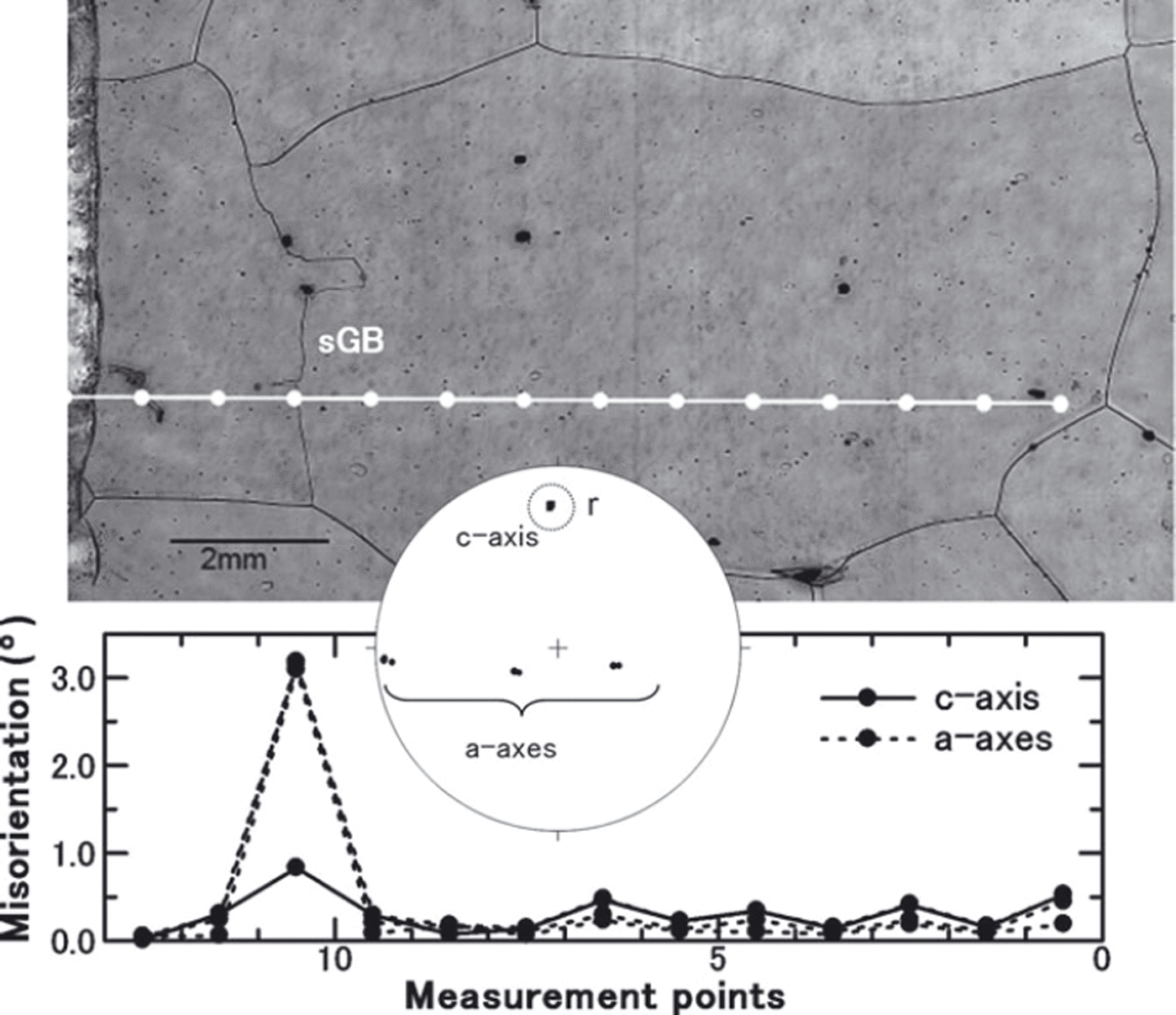
Fig. 7. Sample from the Dome Fuji ice core at 1975 m depth. The upper photo shows the grain with subgrain boundary, which was taken using the microstructure mapping technique (Reference KipfstuhlKipfstuhl and others, 2006). The subgrain boundary (sGB) can be observed as the faint black line compared with the grain boundary. The white dots on the line indicate the measurement points. The lower graph shows the misorientation angle between each adjacent measurement point. All measured orientations are plotted on the stereo net. The orientation of the c-axis from each measurement point in the dotted open circle is almost unchanged, although the measurements are taken across the subgrain boundary. The symbol ‘r’ indicates the rotation axis associated with this subgrain boundary. This is an example of rotation around the c-axis on a subgrain structure.
Further measurements show crystal orientation relations on subgrain boundaries with rotations of ∼2° around one a-axis (Fig. 8). We emphasize that these are the first measurement results of the misorientation angle across subgrain boundaries in ice-core samples. They reveal the characteristics of the orientation relationship across a discrete subgrain boundary such as the previously mentioned misorientation relationship for rotation around the c-axis and one a-axis, and the orientation pattern on the subgrain boundaries can be classified. Each result shows an example of a twist boundary and a tilt boundary as the subgrain rotation mechanism. This microstructure could not be determined without the complete measurement of ice crystal orientation on the subgrain boundaries. Detailed analysis and novel statistics on subgrain boundary mis-orientations in natural Antarctic ice-core samples (EDML (EPICA Dronning Maud Land) ice core) enabled by this new Laue X-ray method, along with microstructure mapping, are described by Reference Weikusat, Miyamoto, Faria, Kipfstuhl, Azuma and HondohWeikusat and others (2011).
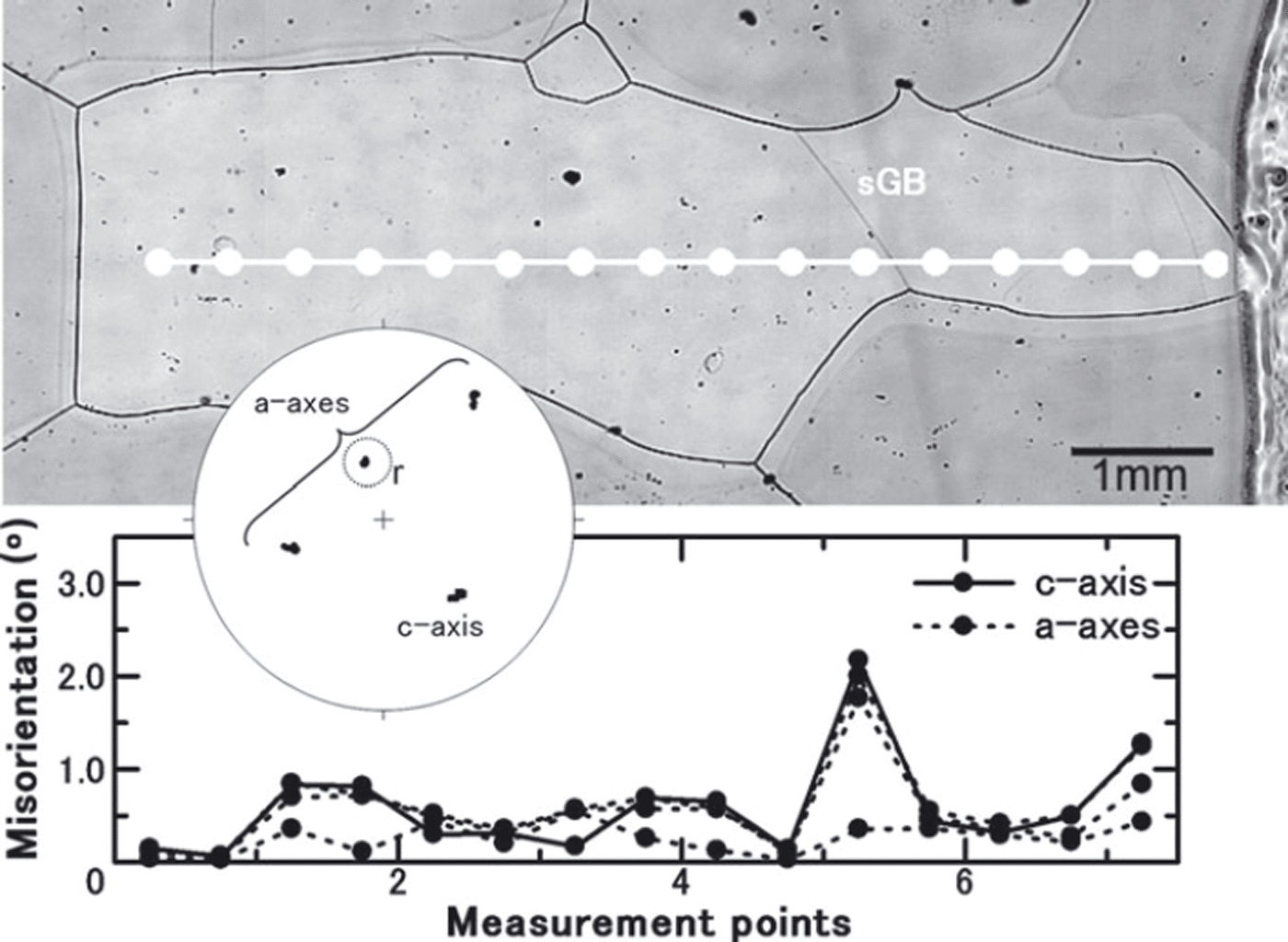
Fig. 8. Sample from the same section as Figure 7. The sample depth is also 1975 m. This is an example of rotation around one a-axis on asubgrain structure.
Conclusion
Our new Laue X-ray diffraction method is customized for analysis of ice-core thin-section samples. It can measure full crystal orientations (c-axis and a-axes) accurately. The important improvements obtained with our new method are:
-
1. Complete determination of ice-crystal orientation, including a-axis.
-
2. Highly accurate measurements compared with traditional methods.
-
3. Application to standard-sized (100 mm × 100 mm) thin-section samples to produce sufficient statistical results and easy combination with standard methods such as microstructure mapping.
-
4. Spatial resolution of ∼0.2 mm, which is less than the grain-size scale of natural polar ice.
-
5. Relative angular resolution of ∼0.5°, which is excellent for grain statistics and below the hypothetical transition between high-angle grain boundaries and subgrain boundaries (Reference SuzukiSuzuki, 1970), relevant for substructure studies.
-
6. Easy procedure. Each step, other than step 1, is completely operable outside the cold laboratory.
-
7. Numerous data points to measure physical properties of ice throughout the ice core, processed in a relatively short time through semi-automatic measurements.
The application of this method for grain statistics and subgrain studies will be a practical and powerful tool for crystallographic study of ice-core samples. The combination of our new method with microstructure mapping (Reference KipfstuhlKipfstuhl and others, 2006) is an important improvement. It is difficult to observe subgrain boundaries between crossed polarizers due to the expected low misorientation angles of less than a few degrees on subgrain boundaries in ice, estimated by grain-boundary energy measurements (Reference SuzukiSuzuki, 1970). Our system will satisfy the demands of ice-core researchers such as Reference KipfstuhlKipfstuhl and others (2006, Reference Kipfstuhl2009), Reference Hamann, Weikusat, Azuma and KipfstuhlHamann and others (2007) and Reference Weikusat, Kipfstuhl, Faria, Azuma and MiyamotoWeikusat and others (2009). Our goal is to make additional improvements toward a fully automated X-ray diffraction analysing system that will further facilitate and accelerate microstructural measurements in ice.
Acknowledgements
This work was supported by Creative Scientific Research (No. 14GS0202) from the Japanese Ministry of Education, Science, Sports and Culture, by Grant-in-Aid for Scientific Research (C) (No. 22540426) from Japan Society for the Promotion of Science and by the German Science Foundation (DGF HA 5675/1-1). We thank S. Nakatsubo and M. Ohi for technical advice and assistance, including the design of the X-ray device and the shutter control instrument. We thank S. Horikawa for support on the Laue image-grabbing program and A. Hori for support on X-ray diffraction measurement. We express appreciation to all members of the GRIP (Greenland) and Dome Fuji ice-core drilling projects. We thank the scientific editor, T. H. Jacka, and three anonymous reviewers for valuable comments and suggestions which improved the manuscript.











