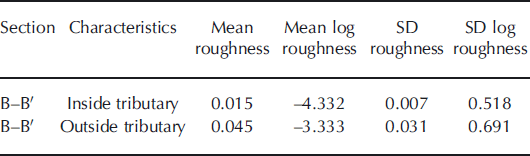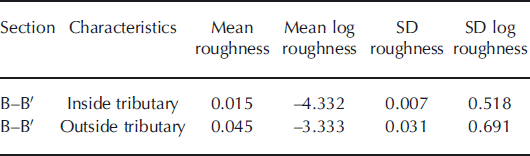Introduction

Basal roughness is the vertical variation in the ice/subglacial-bed interface with distance in the horizontal plane (Reference Siegert, Taylor, Payne and HubbardSiegert and others, 2004, Reference Siegert, Taylor and Payne2005; Reference Taylor, Siegert, Payne and HubbardTaylor and others, 2004; Reference Rippin, Bamber, Siegert, Vaughan and CorrRippin and others, 2006a; Reference Bingham and SiegertBingham and Siegert, 2007, Reference Bingham and Siegert2009; Reference Bingham, Siegert, Young and BlankenshipBingham and others, 2007). In attempting to understand the flow dynamics of ice sheets, and predict future changes, it is critical to understand how roughness variations impact upon ice dynamics. In this paper, we assess the roughness beneath Pine Island Glacier (PIG), which drains ∼175 000 km² of the West Antarctic ice sheet (WAIS; Reference Vaughan, Bindschadler and AlleyVaughan and others, 2001). It consists of a series of tributaries and a main trunk (Fig. 1; Reference Stenoien and BentleyStenoien and Bentley, 2000). Recent thinning and retreat (Reference RignotRignot, 1998; Reference Shepherd, Wingham and RignotShepherd and others, 2004) suggests it may be particularly vulnerable to the rate at which the ocean melts ice close to the grounding line. Close to the grounding line, PIG is particularly fast-flowing (>2.5 km a⁻¹) and shares many features (such as occupying a deep trough) with rapidly changing glaciers in Greenland, such as Jakobshavn Isbræ (Reference Stenoien and BentleyStenoien and Bentley, 2000; Reference Truffer and EchelmeyerTruffer and Echelmeyer, 2003; Reference VaughanVaughan and others, 2006). As a consequence of recent periods of acceleration, PIG is currently no longer in balance, but it is uncertain whether this imbalance indicates the onset of a deglaciation of the basin, or is simply a short-term (multidecadal to century) fluctuation (Reference VaughanVaughan and others, 2006). We have only a limited understanding of the mechanisms behind recent changes, in part because of a lack of data and knowledge of conditions at the bed.

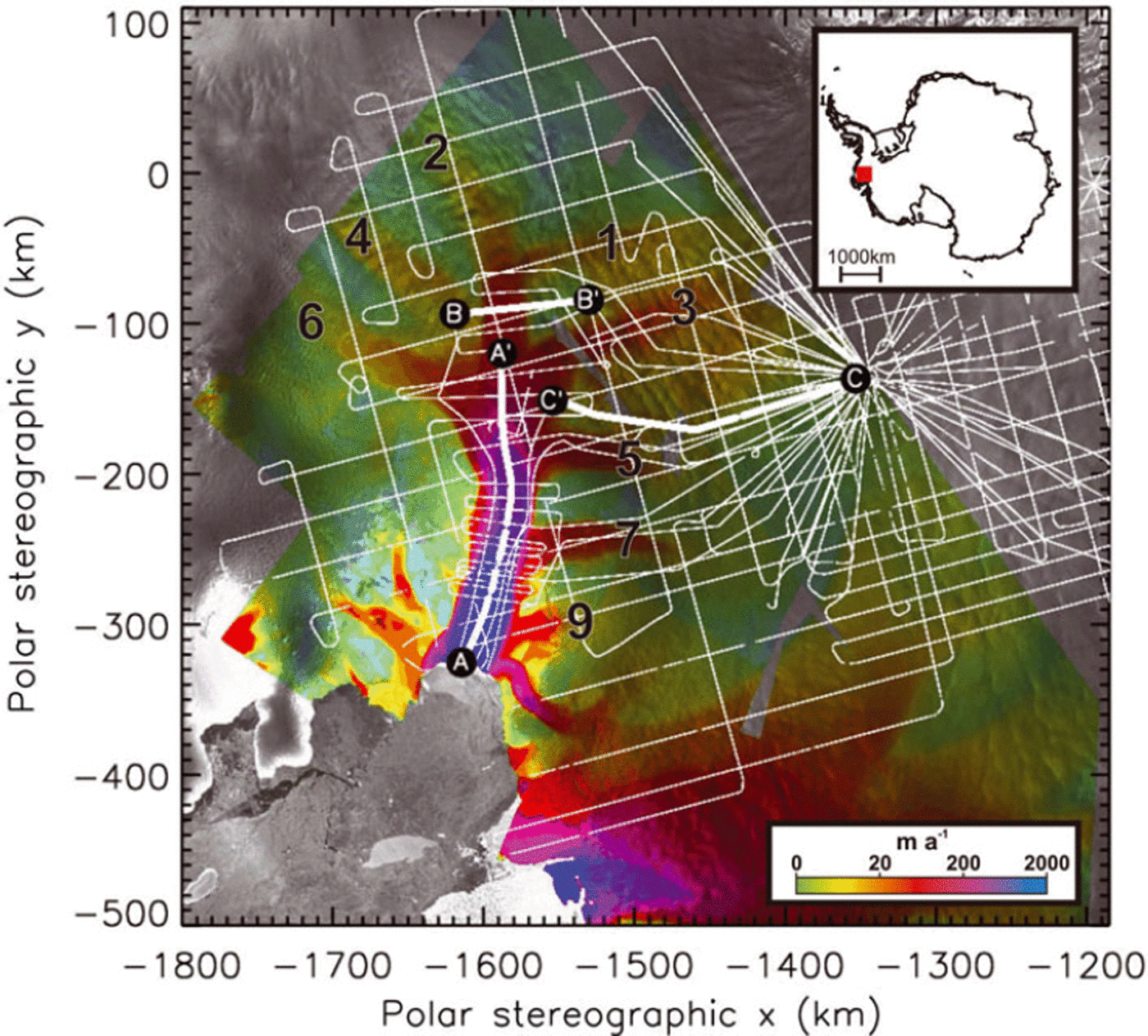
Fig. 1. RES flight tracks (thin white lines) over the Pine Island region. Grey-shaded background shows part of the RADARSAT Antarctic Mapping Project (RAMP) mosaic of Antarctica (K. Jezek and RAMP Product Team, http://nsidc.org/data/nsidc-0103.html), overlain with interferometric synthetic aperture radar (InSAR) velocities (colour shading; Reference RignotRignot and others, 2004). The trunk of PIG is clearly visible as a high-velocity region (blue/purple), with a number of tributaries of lesser velocity (red/yellow). Numbering of the tributaries is according to the scheme originally presented by Reference Stenoien and BentleyStenoien and Bentley (2000; cf. Reference VaughanVaughan and others, 2006). Thick white lines represent sample sections of a single flight line: A–A⁰ represents a section along the trunk of PIG and part of Tributary 2; B–B⁰ is a section directly cutting across Tributary 2, while section C–C’ is a section from a slow-flow region beyond the tributaries (see Fig. 2). Inset shows the location of the study area in Antarctica, marked with a red square.

We are interested in the roughness of the PIG bed because, in general, the resistance that roughness exerts upon ice flow is regionally the most significant stress opposing the glacier driving stress. Since a glacier, or ice sheet, will tend to thicken until the driving stress produces ice flow to maintain the ‘balance flux’, a bed that has a low roughness, and which provides little restraint on ice flow, will achieve balance flux with relatively less thickness and less surface slope. The magnitude of the basal stress exerted by the bed is controlled by roughness and subglacial water pressure (Reference IkenIken, 1981; Reference BindschadlerBindschadler, 1983; Reference LliboutryLliboutry, 1987; Reference JanssonJansson, 1995; Reference WillisWillis, 1995; Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007). While many studies have sought to relate subglacial water pressures to basal motion (e.g. Reference IkenIken, 1981; Reference BindschadlerBindschadler, 1983; Reference JanssonJansson, 1995; Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007), only a few concern the relationship between bed roughness and basal motion; this may in part be due to the difficulty of measuring subglacial roughness (Reference BennettBennett, 2003; Reference Taylor, Siegert, Payne and HubbardTaylor and others, 2004). Bed echoes from radio-echo sounding (RES) across the Antarctic ice sheet (and other ice bodies) provide data from which bed roughness can be assessed. To date, however, only a few researchers have tackled this issue, using a range of methods to extract roughness from bed echoes across a range of scales (e.g. Reference Hubbard, Siegert and McCarrollHubbard and others, 2000; Reference Taylor, Siegert, Payne and HubbardTaylor and others, 2004; Reference Siegert, Taylor and PayneSiegert and others, 2005; Reference Rippin, Bamber, Siegert, Vaughan and CorrRippin and others, 2006a; Reference Bingham and SiegertBingham and Siegert, 2007, Reference Bingham and Siegert2009; Reference Bingham, Siegert, Young and BlankenshipBingham and others, 2007). Our objective is to assess basal roughness beneath the drainage basin of PIG, and the possible future behaviour of the glacier in response to future changes.

Methodology

We used unmigrated data acquired from airborne radio-echo sounding (RES) profiles, collected as part of an aerogeophysical survey of the Amundsen Sea sector of West Antarctica, in the austral summer of 2004/05 (Reference VaughanVaughan and others, 2006). Due to resolution considerations, discussed below, migration was not necessary. Thirty airborne RES sorties were flown over the PIG basin from a field camp and fuel depot located at 77°34′ S, 95°56′ W (Fig. 1). The RES system was fitted in a Twin Otter aircraft, also equipped with dual-frequency carrier-phase GPS for navigation and a radar altimeter for determining surface elevation (Reference VaughanVaughan and others, 2006). The RES system had a transmit power of 4 kW, a centre frequency of 150 MHz, and applied a chirp pulse compression to a coherent stack of 25 sequential traces, giving one trace every 3.2 ms. Every ten traces were incoherently stacked. The resultant data, decimated to give an effective along-track sampling rate of 3 Hz, were then converted to seismic format (SEG-Y). We picked the position of the bed reflectors using the seismic processing package ProMAX. We used a radar wave velocity of 0.168 m ns⁻¹ to calculate ice thickness from two-way travel time, and added 10 m to account for increased speed in firn. More detailed information on the system employed and an overview of the data acquired were reported by Reference VaughanVaughan and others (2006).

Comparisons of ice thickness recorded at flight-line crossover points indicated a root-mean-square (RMS) error of ∼23 m (Reference VaughanVaughan and others, 2006). The RMS crossovers in measurements of ice-surface elevation were considerably lower (∼0.82 m; Reference VaughanVaughan and others, 2006, Reference Vaughan, Rivera, Woodward, Corr, Wendt and Zamora2007), so we take the uncertainty in bed-elevation measurement to be roughly equivalent to that in the ice thickness. The along-track spacing between samples varied as a consequence of variations in the aircraft speed. However, sample spacing was of the order of 15–30 m in most cases.

To assess basal roughness, we applied a forward fast Fourier transform (FFT) to the bed elevations derived from the radar sections (Reference Taylor, Siegert, Payne and HubbardTaylor and others, 2004; Reference Bingham, Siegert, Young and BlankenshipBingham and others, 2007). The approach transforms bed elevation data in a moving window, into the frequency domain using a FFT. Roughness is then defined as the integral of the resultant power spectra in any one moving window (cf. Reference Taylor, Siegert, Payne and HubbardTaylor and others, 2004). There were several steps to the FFT analysis, as follows:

1. 1. We interpolated where there were less than ten consecutive missing points (a gap of less than ∼340 m). Occasional missing data points are not uncommon in RES data because of system errors or an inability to identify the bed reflection. Thus interpolation across small data gaps maintains continuity in the FFT analysis. Where a gap of ten or more points occurred, the line was classified as ‘broken’ and no interpolation was performed. Subsequent FFT analysis was thus restarted down-profile where sufficient sequential data became available.

2. 2. Each section of unbroken line was then resampled at a regular 34 m step size (the approximate mean sample spacing of all flights) to account for the variable sample spacing, and to ensure that smoothing (step 3) occurred over a consistent distance.

3. 3. We removed large-scale topographic variations from the raw data by subtracting a running-mean topography over a moving window of 100 sample points. This resampling created an implicit smoothing over a distance of 3400 m (i.e. 100 × 34 m samples). This approach means we observed roughness over distances that might be classed as local rather than regional, although in reality we were not able to assess roughness over the smallest scales.

4. 4. We performed a FFT over 2 ^N samples, where N = 5. This equates to an FFT window of 32 data points (equal to 1088 m). Several authors (Reference BrighamBrigham, 1988; Reference Taylor, Siegert, Payne and HubbardTaylor and others 2004; Reference Bingham, Siegert, Young and BlankenshipBingham and others 2007) indicate that this is the minimum value of N that should be used. Longer windows are not desirable because they tend to reduce the significance of the shorter-wavelength roughness information, which is of primary interest. As mentioned above, this still only means roughness over scales of the order of 1 km. The measure of bed roughness was then defined as the integral of the resultant FFT of power spectra over each window and was plotted at the centre point of that window.

Bed roughness is undoubtedly present at all spatial wavelengths and a range of amplitudes. Our analysis is sensitive to a specific domain of wavelength-amplitude roughness scales. Consideration of the acquisition characteristics of the system and details of the analysis allows us to estimate the limits of this domain. Firstly, our radar data are fundamentally sensitive only to the along-track roughness; cross-track roughness is largely invisible to us. Secondly, irrespective of spatial wavelength there is a lower limit on the amplitude of the roughness that we can properly measure. This arises from the resolution of the radar system and is unlikely to be better than the mismatches in bed elevation (RMS values) at crossovers, which is ∼23 m. Noise may exist below this level, but it should have a constant amplitude across the entire survey. Thirdly, the maximum and minimum spatial wavelengths of roughness that we can see are limited by the along-track sampling interval (15–30 m originally, resampled at 34 m) and the length of the filtering window (∼1088 m). Finally, the maximum amplitude of roughness that can be seen at a particular spatial wavelength in unmigrated data is limited by the degree to which overlapping hyperbolae allow a bottom echo to be tracked. If the ice bottom is picked as the first basal return (as we have done), then two overlapping hyperbolae produced by point reflectors at a horizontal distance, λ, apart and depth, d, below the ice surface, will obscure any reflector between them that is greater than a depth, β, below them. A simple geometric analysis shows that

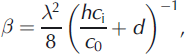
where h is the height of the radar above the ice surface, and c _i and c ₀ are the speed of radar waves in ice and air respectively.

Altogether, the above conditions allow us to fully describe the spatial wavelengths and amplitudes of roughness to which the method we used is sensitive (Fig. 2). This set of scales may not include all those that are likely to affect ice flow, but it does include significant components that might influence ice flow and be altered by the ice flow.

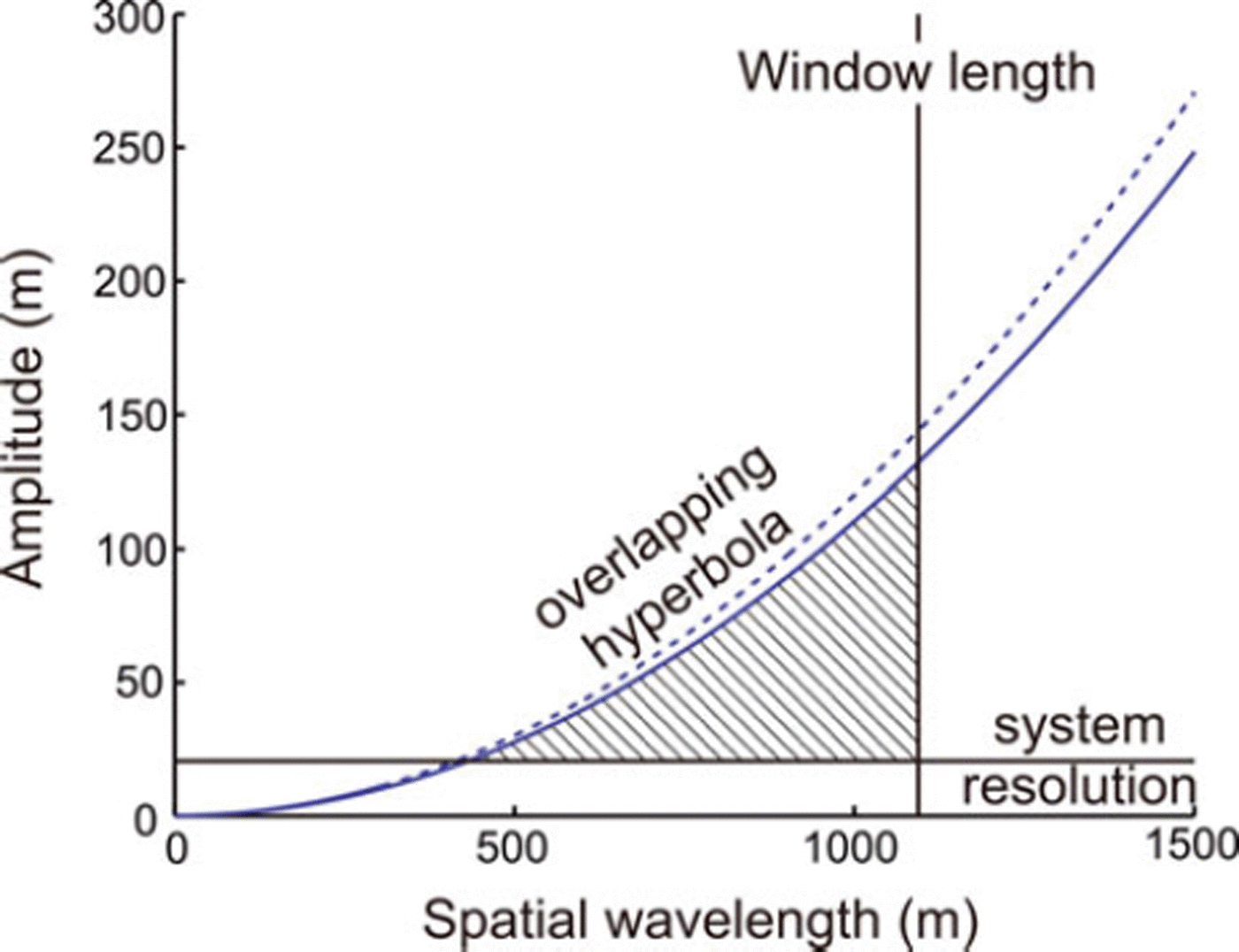
Fig. 2. Indication of the ability of our radar system and processing scheme to discriminate particular spatial wavelengths and amplitudes of basal roughness. The hatched area shows the area of sensitivity, limited by the length of the averaging window, the system resolution, and the effective smoothing implied by overlapping hyperbolae. There is a marginal difference between the aircraft flying at 150m above the ice surface (dashed curve) and 500m above the ice surface (solid curve).

Following the steps outlined above, we analysed roughness along track, and then finally interpolated within the region of study. We gridded the logarithm of our measure of roughness using an inverse-distance weighting procedure, limited to searching in a 20 km radius. Resultant roughness was then compared with modern-day surface velocities and topography.

Results

Figure 3 shows bed elevation and bed roughness along three distinct portions of a single flight (known as B14). Figure 3a is over regions of fast flow along the trunk of PIG and part of Tributary 2; Figure 3b is over a region cutting across Tributary 2; and Figure 3c is over a region of slow flow outside the tributaries (cf. Fig. 1; naming convention is after Reference Stenoien and BentleyStenoien and Bentley, 2000). This flight was chosen because it was recorded along the main trunk and part of a tributary, across the same tributary, and over an extra-tributary area. In each case, resampled bed topography is shown in black, while the along-track bed roughness, calculated as the log of the integral of the power spectra over a 32-point moving window, is overlain in red. Gaps in the data (where FFT analysis could not be carried out) are clearly visible, particularly in Figure 3a and c. The mean roughness of each section is summarized in Table 1. Section B–B’, which crosses Tributary 2, can be subdivided into two sections (at ∼726 km along track), one within the tributary and one outside the tributary. Roughness in these two sections is summarized in Table 2.

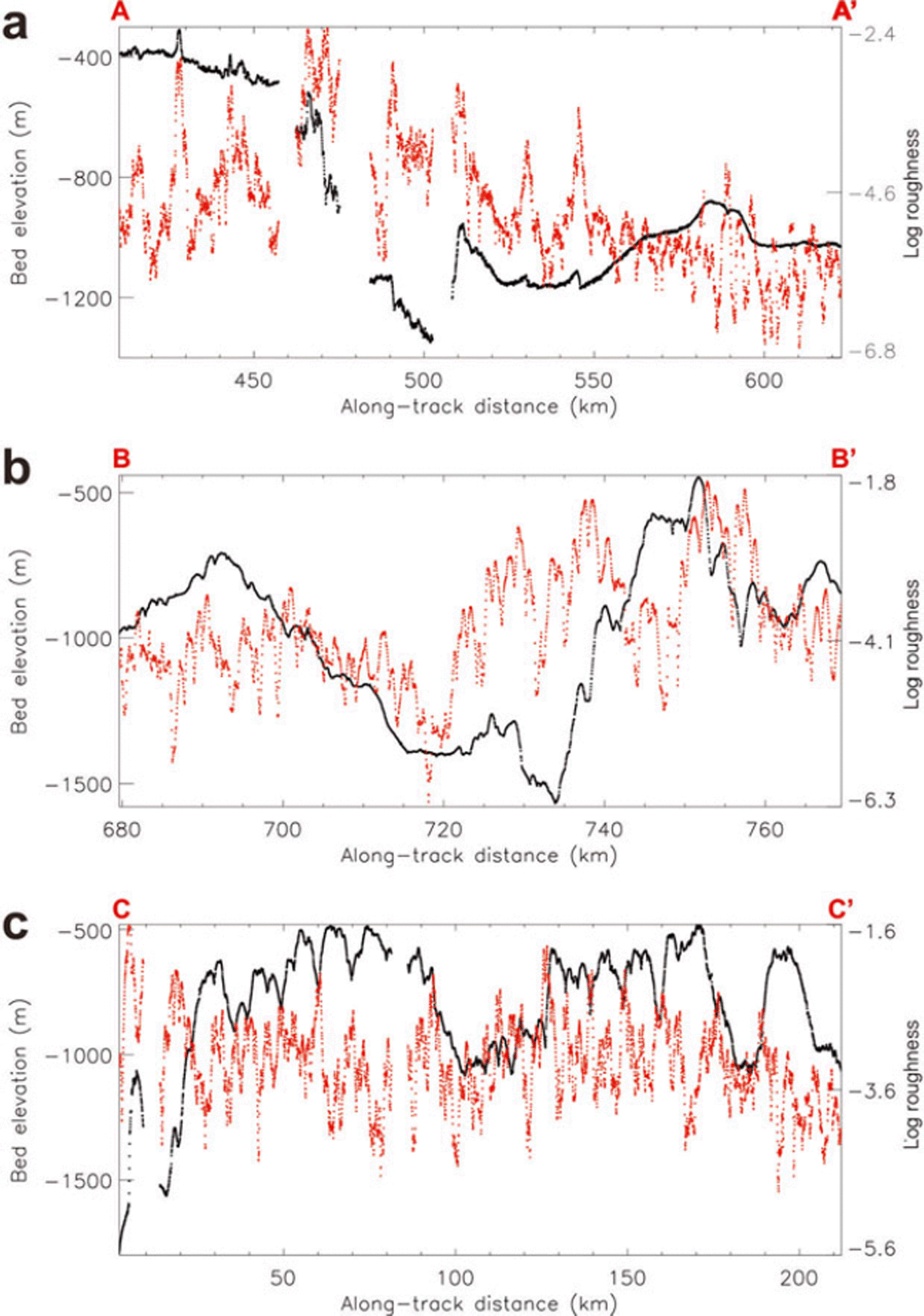
Fig. 3. (a) Raw bed elevation (black) and roughness (red) properties along flight-line section A–A⁰. The roughness is the integral of the power spectra at the centre point of a 32-point-wide moving window. (b) and (c) are identical to (a), but for sections B–B⁰ and C–C⁰ respectively.

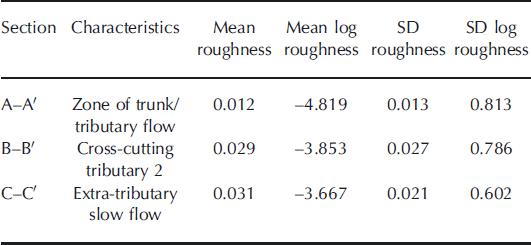
The summary data in Tables 1 and 2 indicate that the bed is roughest where velocities are lowest (section C–C’ and the extra-tributary part of section B–B’). The smoothest bed occurs where ice flow is fastest, i.e. in section A–A’, directly along the main trunk of PIG and Tributary 2, and also the part of section B–B’ found within Tributary 2. Roughness is indicated both by the lower calculated roughness values, and also as generally indicated by reduced roughness variability (indicated by the standard deviation). Conversely, rougher beds have higher roughness values and generally greater variability.

Figure 4a shows bed topography (after Reference VaughanVaughan and others, 2006), while Figure 4b shows roughness contoured and shaded over the whole of PIG. The quantity shown here is the log of our roughness measure, gridded using an inverse-distance weighting procedure that was limited to searching in a 20 km radius. Figure 4c shows interferometric synthetic aperture radar (InSAR) velocities (after Reference RignotRignot and others, 2004). Roughness is derived from 33 separate flight-lines (including the one analysed in detail above), covering >35 000 km (Reference VaughanVaughan and others, 2006). From the gridded data, roughness was then extracted along the centre line of each tributary. Figure 5 shows plots of surface velocity, bed elevation and bed roughness along each tributary, extracted from the map of interpolated roughness shown in Figure 4b.

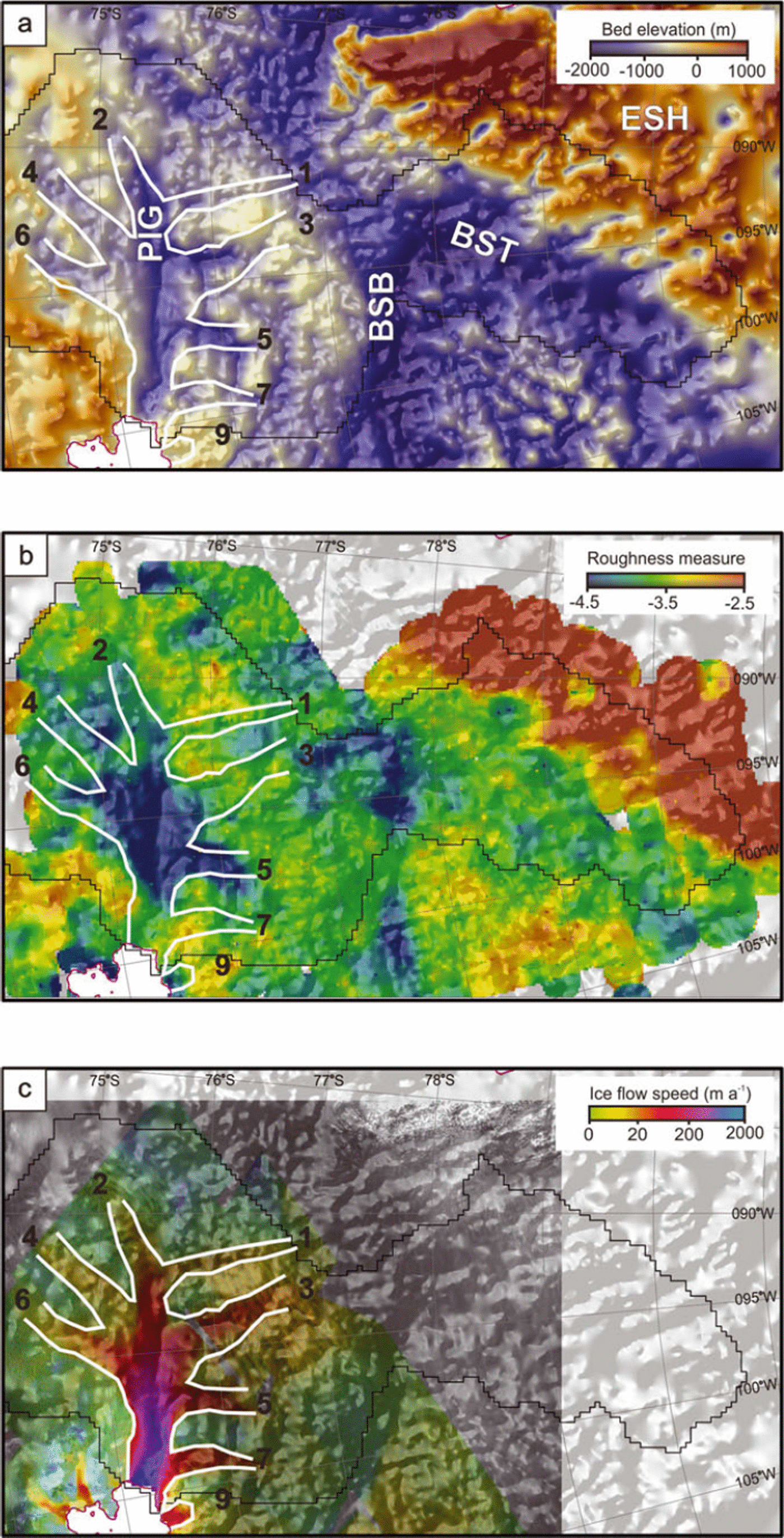
Fig. 4. (a) Bed topography across the whole PIG region (after Reference VaughanVaughan and others, 2006). This topography was constructed from a compilation of data from many sources, gridded with a simple inverse-distance weighting algorithm. PIG is Pine Island Glacier, BSB is the Byrd Subglacial Basin, BST is the Bentley Subglacial Trench and ESH is the Ellsworth Subglacial Highlands. The tributaries of PIG are numbered in order to aid comparison with Figure 4b and c. Numbering is according to the scheme originally presented by Reference Stenoien and BentleyStenoien and Bentley (2000; cf. Reference VaughanVaughan and others, 2006). (b) Log of bed roughness across the PIG region. More negative numbers indicate a smoother bed, while less negative numbers indicate a rougher bed. Again, the tributaries of PIG are numbered to aid comparison with Figure 4a and c. (c) InSAR velocities (where available) across the region (after Reference RignotRignot and others, 2004). Again, tributary numbering aids comparison with Figure 4a and b.

Fig. 5. Plots of surface velocity, bed elevation and bed roughness along the main PIG trunk and all the major tributaries. (a) The location of each along-tributary section (background colouring represents InSAR velocities (after Reference RignotRignot and others, 2004)); tributaries are again numbered according to the scheme of Reference Stenoien and BentleyStenoien and Bentley (2000). (b–h) The three boxed line-charts show (from top to bottom): surface velocity, bed elevation and the log of roughness for: (b) Tributary 1; (c) Tributary 2 and the main glacier trunk (starting at the upper limit of Tributary 2 and ending near the grounding line of the main trunk); (d) Tributary 3; (e) Tributary 4; (f) Tributary 5; (g) Tributary 6; and (h) Tributary 7. Data were extracted from the gridded data shown in Figure 4. The x-axes in all line-charts represent along-tributary distance, with the right-hand side (maximum value) representing the point where the tributary joins the centre of the main PIG trunk. Note that the y-axis scaling on all roughness plots is identical, to aid comparison, unlike the y-axis for the other quantities. Regions shaded transparent red represent areas of low roughness referred to in the text.

A zone of low roughness is located in the central trunk of PIG and in much of the length of Tributary 5 and part of Tributary 6 which feed the main trunk (Figs 4b and 5f and g). Elsewhere within PIG (and the other tributaries), roughness is markedly higher, even though velocities are comparable to those on Tributaries 5 and 6. In Figure 5d and e, the lower parts of Tributaries 3 and 4 also appear smooth (shaded red), but this is where the tributaries meet the main trunk of PIG. In the tributaries themselves, roughness is higher. Outside PIG, there are also two distinct regions within the deep Byrd Subglacial Basin (BSB; Fig. 4a and b) that exhibit low roughness, but the adjacent Bentley Subglacial Trench is characterized by high roughness. Finally, the Ellsworth Subglacial Highlands are associated with particularly high roughness values (Fig. 4a and b).

Figure 6 shows the relationship between surface velocity and basal roughness in each of the tributaries, as defined in Figure 5a. In Tributaries 3, 4 and 6 (Fig. 6c, d and f) particularly, velocity and roughness are related, with roughness decreasing exponentially as velocity increases, i.e. log of roughness becomes more negative. This relationship indicates a strong association between a smooth bed and fast flow. The relationship is less clear in the other tributaries and the main trunk, reflecting the fact that in some locations higher velocities are associated with a rough bed.

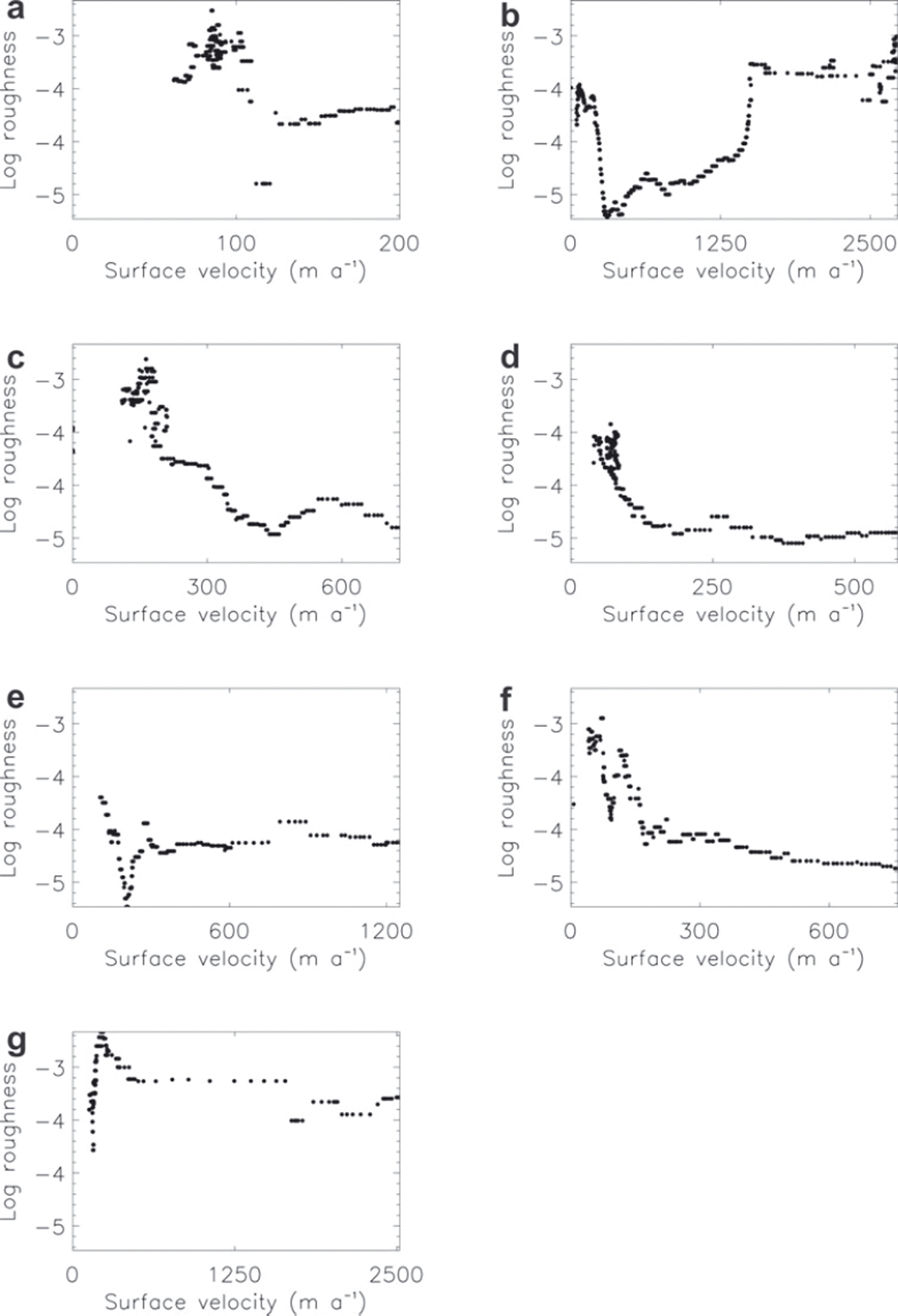
Fig. 6. Variation in basal roughness with velocity along the tributaries shown in Figure 5a. (a) Tributary 1; (b) Tributary 2 and the main glacier trunk; (c) Tributary 3; (d) Tributary 4; (e) Tributary 5; (f) Tributary 6; and (g) Tributary 7.

Discussion

To gain insight into the influence of bed roughness on ice flow, we consider the range of processes that might cause a rough or smooth bed. Reference Bingham and SiegertBingham and Siegert (2009, their fig. 3) detail some ideas. Of primary importance is the possibility of marine inundation following collapse or disappearance of the WAIS in the Pliocene or Pleistocene (e.g. Reference Scherer, Aldahan, Tulaczyk, Possnert, Engelhardt and KambScherer and others, 1998; Reference Pollard and DeContoPollard and DeConto, 2009). This would cause a smooth bed of marine sediments. Conversely, a rougher bed suggests no marine sedimentation. Reference Pollard and DeContoPollard and DeConto (2009) do indeed show that the Pine Island area was deglaciated ∼200 ka BP, and Reference VaughanVaughan and others (2006, their fig. 1f) show that virtually the entire PIG basin was palaeoseabed in the past. Both observations strongly support the presence of marine sediments across large parts of the PIG bed.

A set of linked factors responsible for variations in bed roughness are ice dynamics, thermal regime and subglacial erosion/deposition. A smooth bed is thus related to high rates of basal erosion, as a result of faster flow, facilitated by a warmer thermal regime. Conversely, a rough bed would be a consequence of minimal erosion due to cold, slower-moving ice (Reference Bingham and SiegertBingham and Siegert, 2009). Below, we consider our results in light of these interpretations.

Conclusions

We have used a new RES dataset from the Amundsen Sea sector of West Antarctica to investigate basal roughness in the vicinity of PIG. In line with other workers, we interpret a smooth bed to indicate significant deposits of marine sediments, laid down following collapse or disappearance of the WAIS ∼200 ka BP.

Although our analysis suggests a link between ice velocity and bed roughness, such that velocities are higher where the bed is smoother, and lower where the bed is rougher, we suggest only an indirect relationship between the two. In other words, a smooth bed does not directly produce high rates of ice flow, but rather the need for a lower driving stress to achieve the balance flux. As a consequence, the surface is lower and so ice is drawn down from surrounding rougher areas into this smooth area. The fact that roughness varies widely across the PIG tributaries suggests that velocity changes on the main trunk will be differentially transmitted back into the interior along them.

We also verify the modelled basal drag fluctuations, determined by other workers, indicating that elevated basal drag in PIG may be a result of increased basal roughness (Reference Vieli and PayneVieli and Payne, 2003; Reference Thomas, Rignot, Kanagaratnam, Krabill and CasassaThomas and others, 2004). Our work also supports modelling studies that identify patchy bed conditions in which roughness and thus resistance to flow varies over short distances (cf. Reference JoughinJoughin and others, 2009).

Ice-stream reorganization and migration has been reported from the Siple Coast region of West Antarctica (e.g. Reference Conway, Catania, Raymond, Scambos, Engelhardt and GadesConway and others, 2002; Reference Christoffersen and TulaczykChristoffersen and Tulaczyk, 2003; Reference Catania, Conway, Raymond and ScambosCatania and others, 2005). This is possible because of the minimal topographic restrictions on the Siple Coast ice streams, meaning they are able to laterally migrate relatively easily (Reference Catania, Conway, Gades, Raymond and EngelhardtCatania and others, 2003). In the case of PIG, however, Reference VaughanVaughan and others (2006) suggested that it is unlikely that a collapse initiated along the trunk would extend into the deepest parts of the WAIS, because the trunk and tributaries of PIG lie in deep, confining subglacial troughs and are enclosed by a ridge in the bed topography. Our roughness assessment supports this, since a lack of smooth bed beyond the current limits of PIG and its tributaries indicates that any substantial increase in ice velocity due to basal sliding would not extend here, or at least that it would not be favoured in these rough-bed areas. We propose that PIG and its contributing tributaries could be considered as relatively stable West Antarctic fast-flow features (in terms of their location and extent), but that any dynamic response due to changes in ice flux would be felt with significant spatial variability in PIG, such that different tributaries, and indeed different parts of tributaries and the trunk, would speed up to different degrees. Thus, exploration of future dynamics changes in PIG should focus on the likely variability of these responses. Beyond work in PIG, indentifying areas of bed undergoing active smoothing would be of great benefit for investigations into the causal link between basal roughness and ice dynamics.