Introduction
The importance of glaciers as contributors to global sea-level rise is well recognized (Reference SolomonSolomon and others, 2007) and several authors have presented methods of assessing recent and modeling future glacier wastage on a global scale (e.g. Reference Van de Wal and WildVan de Wal and Wild, 2001; Reference Raper and BraithwaiteRaper and Braithwaite, 2006; Reference MeierMeier and others, 2007). Since volume observations are available only for a limited number of glaciers, while data on surface areas are far more abundant, a common way to estimate glacier volume is through a scaling relationship between glacier volume and area. Reference Bahr, Meier and PeckhamBahr and others (1997) derived power-law scaling relationships between the steady-state volume of a glacier and its area and length. Although scaling exponents may change under non-steady-state conditions, scaling has commonly been used in future volume projections on a global scale (e.g. Reference Van de Wal and WildVan de Wal and Wild, 2001; Reference Raper and BraithwaiteRaper and Braithwaite, 2006; Reference MeierMeier and others, 2007; Reference SolomonSolomon and others, 2007) since the input data required for more sophisticated approaches are generally not available.
Volume–area scaling improves projections assuming constant glacier area in time (e.g. ACIA, 2004). Keeping the area fixed in time does not allow the glacier to reach new equilibrium in a different climate while the scaling, coupled with the mass-continuity equation, allows for changes in glacier size. Therefore, scaling accounts for at least some of the feedback between glacier mass balance and geometry as the glacier size and shape adjust to climate change. The area-averaged surface mass balance of a glacier will change as the glacier thins and retreats or thickens and advances, until it has reached a new equilibrium geometry in response to a step-like climate perturbation, but there are two opposing effects. By lowering the ice surface as the ice thins, the glacier is exposed to higher air temperatures, resulting in more-negative mass balances. However, as the glacier retreats, loss of area at predominantly lower altitudes will make the area-averaged mass balance less negative (Reference Braithwaite and RaperBraithwaite and Raper, 2002). Reference Raper, Brown and BraithwaiteRaper and others (2000) developed a ‘geometric’ model including scaling relationships between glacier volume, area and length. This model, forced by Global Climate Model (GCM) scenarios, reduced the estimated global glacier ablation for the end of the 21st century by ∼45% compared with results when the glacier area was kept constant in time, in agreement with the range of 40–50% reported by Reference SolomonSolomon and others (2007).
Despite the dominance of scaling methods in attempts to estimate global glacier volumes and future glacier wastage, very little effort has been devoted to a systematic error analysis of the results derived from scaling relationships. For example, Reference Van de Wal and WildVan de Wal and Wild (2001) compared the scaling method with an ice-flow model for several individual glaciers and reported that a retreating glacier is at any arbitrary time not more than 20% smaller in volume than expected from volume–area scaling. Reference Schneeberger, Blatter, Abe-Ouchi and WildSchneeberger and others (2003) performed a similar comparison between the volume–area scaling and a two-dimensional (2-D) ice-flow model for 11 glaciers. Since volume projections by the scaling method were both over- and underestimated, depending on how well a particular glacier in their sample fit in the scaling relationship, they concluded that the scaling method should be applicable on a large dataset. Reference MeierMeier and others (2007) applied scaling to a global dataset and reported an error in calculating volumes from area values ∼25% for global aggregates, but ∼50% for individual ice masses. However, none of these studies provided any details of how error estimates were derived or a systematic evaluation of the scaling methods.
Reference Pfeffer, Sassolas, Bahr and MeierPfeffer and others (1998) used a pseudo-three-dimensional (pseudo-3-D) ice-flow model for synthetic glaciers in steady state to test whether the scaling relationships of Reference Bahr, Meier and PeckhamBahr and others (1997) were derived correctly from the underlying continuum mechanics. Although they confirmed the physical background of the scaling relationships, they did not perform an error analysis nor apply the model to real glaciers. Another study on synthetic glaciers, by Reference Radić, Hock and OerlemansRadić and others (2007), compared volume evolutions derived from a scaling method with those derived from a one-dimensional (1-D) ice-flow model. Results indicated that the volume projections derived from scaling were relatively insensitive to the assumptions of scaling exponents. In this paper, we elaborate on their analysis using a set of real glaciers in order to investigate the uncertainties in modeling future glacier volume changes from the scaling methods. Our aim is to present a detailed analysis of the performance of scaling relationships between glacier volume, area and length used for deriving volume projections in comparison with projections from an ice-flow model.
Methods
A 1-D ice-flow model along a flowline (Reference OerlemansOerlemans, 1997) is applied to produce volume evolutions which serve as a reference to which volume evolutions derived from the scaling methods are compared. Our procedure can be divided into four steps: First, we calibrate the ice-flow model by varying the glacier mass-balance profiles to maximize the agreement between both observed and simulated glacier historical length fluctuations and recent glacier surface profile along the flowline. Second, we impose hypothetical mass-balance perturbations on the reference mass-balance profile, defined as a negative trend in the mass-balance rate, and derive 100 year volume evolutions from the ice-flow model. Third, results are compared with the volume evolutions derived from scaling methods using the same mass-balance perturbations. We use three different scaling methods: volume–area scaling, volume–length scaling and volume–area–length scaling. Finally, we apply a series of model experiments in order to investigate the sensitivity of volume evolutions to the choice of scaling parameters and to the way mass-balance–elevation feedback is incorporated.
Investigated glaciers and data
For this study we selected six glaciers from different geographical locations and climatic regimes for which the required input data could be retrieved: Nigardsbreen (61.72° N, 7.13° E), an outlet glacier of Jostedalsbreen in southern Norway; Rhonegletscher (46.62° N, 8.40° E) in the center of the Swiss Alps; South Cascade Glacier (48.37° N, 121.05°W) in the North Cascades of Washington State, USA; Sofiyskiy glacier (49.78° N, 87.77° E), a continental summer-accumulation-type glacier in the Russian Altai mountains; midre Lovénbreen (78.88° N, 12.07° E) a polythermal valley glacier in northwest Spitsbergen, Svalbad and Abramov glacier (39.67° N, 71.50° E) in the Alay range of Kyrgyzstan. The surface maps of these glaciers are shown in Figure 1.

Fig. 1. Contour maps of the investigated glaciers based on topographic maps. The year gives the date of the topographic map.
To run the ice-flow model, data on bed and surface topography, historical front observations and mass balance are needed. The ice-flow model has previously been applied to Nigardsbreen (Reference OerlemansOerlemans, 1997), Rhonegletscher (Reference Stroeven, van de Wal, Oerlemans and OerlemansStroeven and others, 1989; Reference Wallinga and van de WalWallinga and Van de Wal, 1998) and Sofiyskiy glacier (Reference De Smedt and PattynDe Smedt and Pattyn, 2003), and their input data were available for this study. Unless otherwise stated, mass-balance data were taken from the reports of the World Glacier Monitoring Service (WGMS; e.g. Reference Haeberli, Zemp, Frauenfelder, Hoelzle and KääbHaeberli and others, 2005) and from the reports of the Norwegian Water Resources and Energy Directorate (e.g. Reference KjøllmoenKjøllmoen, 2001). The digital elevation model for the surface of South Cascade Glacier and observations of mass-balance profiles were taken from United States Geological Survey reports (e.g. Reference KrimmelKrimmel, 2002; Reference Bidlake, Josberger and SavocaBidlake and others, 2004). The bed topography map was provided by B. Krimmel (unpublished data), while the historical front observations were compiled by Reference Rasmussen and ConwayRasmussen and Conway (2001). The bed topography of midre Lovénbreen was derived from ground-penetrating radar data (Reference BjørnssonBjörnsson and others, 1996; J. Moore, unpublished data), while the surface topography maps were compiled by the Norsk Polarinstitutt from aerial photographs made from several time periods as explained by Reference RippinRippin and others (2003). Interpolated mass-balance profiles for midre Lovénbreen were provided by J. Kohler (unpublished data). Reference Kuzmichenok, Vasilenko, Macheret and MoskalevskiyKuzmichenok and others (1992) produced the bed and surface topography maps for Abramov glacier, while the observed mass-balance profiles were compiled by Reference PertzigerPertziger (1996). In Table 1 we list, for these six glaciers, the time periods for which the data of length fluctuations and mass balance are available and the years of the surface and bed topography maps used in the calibration of the ice-flow model. Some data on ice velocities are available for Rhone, South Cascade and Sofiyskiy glaciers and are used to calibrate the ice-flow model.
Table 1. Observational time periods used in the flowline model for the six glaciers, Nigardsbreen (NIG), Rhonegletscher (RHO), South Cascade Glacier (SCG), Sofiyskiy glacier (SOF), midre Lovénbreen (ML) and Abramov glacier (ABR); flow parameters derived from the dynamical calibration; and modeled values of volume, V, area, A, and length, L, at the end of the calibration periods, i.e. prior to the 100 year mass-balance perturbations. b is area-averaged mass balance averaged for each glacier over the period of mass-balance observations

Volume evolutions from the ice-flow model
Model description
For each of the six glaciers we used the 1-D ice-flow model (central flowline along x) of Reference OerlemansOerlemans (1997). The time-step was 0.005 years, and gridpoint spacing along the flowline was 100 m. The 3-D geometry was taken into account by parameterization of the cross-sectional geometry at each gridpoint. The cross-profile has a trapezoidal shape and is described by the valley width at the base, w b, glacier thickness along the flowline, H, and the angle between the valley wall and the vertical, θ. Values for the width at the glacier’s surface, w s, and for θ were calculated from topographic maps. The width at the base was parameterized as a function of H:
For Sofiyskiy glacier the surface width derived from the topography map was kept constant in time due to lack of bed topography data. The driving equation for calculating volume evolutions from the model is the continuity equation which, assuming constant ice density, can be written as:
where S is the cross-sectional area of the glacier defined by
U is the depth-averaged ice velocity and ![]() is the specific mass-balance rate. U is calculated as (Reference Budd, Keage and BlundyBudd and others, 1979; Reference PatersonPaterson, 1994):
is the specific mass-balance rate. U is calculated as (Reference Budd, Keage and BlundyBudd and others, 1979; Reference PatersonPaterson, 1994):
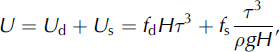
where subscripts ‘d’ and ‘s’ refer to internal deformation and basal sliding, respectively, τ is the local ‘driving stress’ which is proportional to the ice thickness, H, and surface slope, ∂h/∂x, ρ is ice density (ρ = 0.9 kg m−3) and g is acceleration due to gravity. The flow parameters f d and f s depend on bed conditions, debris content and crystal structure of the basal ice layers, but their values are not known accurately. Therefore we use these flow parameters as tuning parameters to achieve the closest match between the observed and modeled surface profiles along the flowline. Substitution of Equations (1) and (3) into Equation (2) yields the prognostic equation for the glacier thickness, H:

which we used for deriving volume evolutions.
Dynamical calibration
Following Reference OerlemansOerlemans (1997) the ice-flow model was calibrated using so-called dynamical calibration. This technique consists of minimizing the difference between modeled and observed historical front variations by experimentally determining a stepped mass-balance variation forcing, thus allowing a rough reconstruction of the recent mass-balance history. For a successful calibration it is necessary that the available record of glacier length, L, exceeds the characteristic glacier’s response time which is of the order of several decades for our study glaciers (Reference OerlemansOerlemans, 2001). For the recent period with available mass-balance observations we applied the observed annual net mass-balance profiles, b(h, t), as an input to the model. For the prior period, we averaged the observed mass-balance profiles over the total period of available observations and described the mean annual mass-balance profile by a polynomial function of glacier surface elevation, h. This polynomial function served as a reference annual mass-balance profile, b ref(h), in the simulations of the historic front variations. The model was calibrated by introducing a stepped perturbation, Δb(t), to a reference mass-balance profile so the annual mass-balance profile along the flowline is:
Table 1 shows the periods over which we averaged the mass-balance profiles and calculated b ref(h) for each glacier, and the reference mass-balance profiles are shown in Figure 2. The calibration, i.e. tuning of flow parameters f d and f s and mass-balance perturbations Δb(t), is considered successful if the modeled front variations and surface profile at the year of the surface map (Fig. 1) yield the closest possible match to the observations. Additional control parameters for the dynamical calibration were the observed surface velocities, which provided an expected order of magnitude for the modeled vertically averaged velocities. More details on this optimization are given by Reference OerlemansOerlemans (1997). For midre Lovénbreen and Abramov glacier the flowline model was calibrated to best match the observed and modeled thickness profiles because a long-term record of front variations is missing.

Fig. 2. Reference mass-balance profiles, b ref, as a function of surface elevation, h, for Nigardsbreen (NIG), Rhonegletscher (RHO), South Cascade Glacier (SCG), Sofiyskiy glacier (SOF), midre Lovénbreen (ML) and Abramov glacier (ABR).
In Figure 3 we present the results of the dynamical calibration, i.e. the observed and simulated historical glacier lengths and corresponding perturbations in mass-balance profile, Δb, as a deviation from the reference mass-balance profile, b ref(h). Since we used the same input geometry data for Nigardsbreen, Rhonegletscher and Sofiyskiy glacier as in the previous studies (Reference OerlemansOerlemans, 1997; Reference Wallinga and van de WalWallinga and Van de Wal, 1998; Reference De Smedt and PattynDe Smedt and Pattyn, 2003) we obtained very similar simulations with almost identical flow parameters. For these three glaciers a good match between the observed and the modeled historical lengths was obtained. For South Cascade Glacier, deviations were large in the first 50 years of the simulation. This was attributed to the lack of reliable bed topography data beyond the current glacier extension and the existence of a lake ∼1 km downstream of the current glacier snout into which the glacier was calving in the first half of the 20th century. Therefore we put more emphasis on simulating the length fluctuation in the last 50 years, in order to accurately reproduce the glacier’s recent retreat. Figure 4 presents the observed and simulated thickness profiles for all six glaciers, each in the year of the respective surface map (Fig. 1). Although the match between observed and modeled surface profiles was not entirely satisfying, these were the best results with respect to optimal agreement between modeled and observed glacier-length fluctuations. The flow parameters obtained through the calibration are listed in Table 1 with the modeled volume, area and length at the end of the calibration period including the area-averaged mass balance for the reference mass-balance profile b ref(h). The modeled A and L were, respectively, within ±20% and ±15% of those reported in the glacier inventory by the World Glacier Monitoring Service (e.g. Reference Haeberli, Zemp, Frauenfelder, Hoelzle and KääbHaeberli and others, 2005).

Fig. 3. Results of the dynamic calibration for four glaciers. The observed (thick curve) and modeled (thin curve) length fluctuations are presented in the upper graph for each glacier, while the lower graphs show the reconstructed perturbations in the mass-balance profiles, Δb, derived from the dynamical calibration (Equation (6)).

Fig. 4. Observed (solid curve) and modeled (dashed curve) surface elevations and bed along the flowline. The dates for the observed surface profiles are the same as in Figure 1.
Volume projections
The last year of the dynamical calibration is the initial year of volume projections forced by hypothetical mass-balance perturbations (see last year in ‘Length fluctuations’ column in Table 1). At the initial year (t = 0) with the corresponding glacier volume, V(t = 0), we introduced a hypothetical trend-like mass-balance scenario in the flowline model by perturbing the annual mass-balance profile according to Equation (6). The magnitude of future mass-balance profile perturbation, Δb, increases with a constant rate:
where t = 1, …, 100 years. A period of 100 years was chosen because future climate-change studies are often focused on a century scale. Following Reference Radić, Hock and OerlemansRadić and others (2007) we chose three different rates of mass-balance profile perturbation, Δb(0), equal to −0.005, −0.010 and −0.015 m a−1 which are applied on all six glaciers, and correspond to perturbations of −0.5, −1.0 and −1.5 m, respectively, after 100 years. Hence, we did not consider glacier response to real climatic changes which differ from glacier to glacier but we ‘homogenized’the response. Thus, we assumed a climate-change scenario which produces identical changes in the mass-balance profiles of all six glaciers.
Although the dynamical calibration gives one of many possible solutions for the tuning parameters, it creates a glacier state that corresponds to the state of response to recent climate forcing. This implies that a steady-state assumption is not needed, i.e. the glacier need not be in steady state prior to application of the mass-balance perturbation for the 100 year projections. Thus the flowline model allows the glacier to have a ‘memory’.
Volume evolutions from the scaling methods
Scaling relationships
Since the required input data for ice-flow modeling are seldom available, alternative methods have been developed to account for glacier geometry changes in volume projections. A commonly used approach is based on scaling relationships between glacier characteristics such as volume, area, length, width and mean thickness. Using models that assume perfect plasticity, Reference OerlemansOerlemans (2001) investigated the relationships between thickness, length, slope, mass-balance gradient and response times for glaciers and ice caps. Initially, the scaling exponents in the volume–area and width–length relationships were derived from glacier inventory data (e.g. Reference Macheret, Cherkasov and BobrovaMacheret and others, 1988; Reference Chen and OhmuraChen and Ohmura, 1990). The relationships were investigated by Reference BahrBahr (1997b) and Reference Bahr, Meier and PeckhamBahr and others (1997) and shown to be based on a theoretical analysis of glacier dynamics and glacier geometry. The volume, V, of a valley glacier without calving and without hanging or discontinuous longitudinal profiles is related to its surface area, A, and its length, L, via a power law:
According to Reference Bahr, Meier and PeckhamBahr and others (1997) the scaling exponents are γ = 1.375 and q = 2.2, while c a and c l are constants of proportionality. These two relationships are equivalent, provided that width–length scaling is applied such that the characteristic (average) width, [w], is proportional to L 0.6. Based on glacier inventory data and measured volumes through radio-echo-soundings (e.g. Reference Macheret and ZhuravlevMacheret and Zhuravlev. 1982), Reference Chen and OhmuraChen and Ohmura (1990) found average values of γ = 1.357 and c a = 0.2055 m3−2γ for 63 mountain glaciers. Values ranged between 1.15 and 1.52 for γ and between 0.12 and 0.22 m3−2γ for c a for different regions. Using a probability-density function for c a, derived from volume and surface area data for 144 glaciers around the world, Reference BahrBahr (1997a) found the mean of the distribution to be 0.191 m3−2γ and the standard deviation to be 0.073 m3−2γ , where γ = 1.375. Corresponding values for the constant c l in Equation (9) could not be found in the literature.
Volume projections
We applied the scaling relationships in order to derive volume evolutions for our six glaciers forced by the same hypothetical climate scenario as applied in the flowline modeling. The input data were the initial volume, area and length of the glacier or at least one of these characteristics since the scaling enables us to derive one characteristic from another. Additionally, the mass-balance profile and the area–elevation distribution were required. Thus, starting from t = 0 and applying the same mass-balance profile perturbations, Δb, to the annual mass-balance profile, b(h, t), as above, we calculated the volume change at any year t as:

This is the discretized mass continuity equation with constant ice density where bi (t) is the annual specific mass balance of the ith elevation band which corresponds to b(h, t), while ai (t) is the area of the ith band and n the total number of bands. Elevation bands were equally spaced (100 m) along the flowline (x axis) to correspond to the elevation bands in the ice-flow model. For each elevation band we know its length along the flowline, elevation and area. The sum of all the area bands is equal to the total surface area A(t):

Based on the mass balance obtained from Equation (6) for any year t a new volume at t+ 1 was calculated as:
We applied three different methods for determining the glacier area and the number of bands, n, via the scaling relationships: (1) volume–area scaling, (2) volume–length scaling and (3) volume–area–length scaling which combines (1) and (2).
1. Volume–area (V-A) scaling
The volume–area relationship (Equation (8)) was used to derive the glacier’s area for year t + 1:

We assumed that the glacier area–elevation distribution remains constant and any change in area occurs only at the glacier front. Elevation bands were subtracted (if the glacier retreated) or added (if the glacier advanced) at the glacier front. We derived the new number of bands, n, from Equation (11). Reference Radić, Hock and OerlemansRadić and others (2007) applied this method for volume evolution of synthetic glaciers with simplified geometry and showed that the mass-balance/area–elevation feedback is captured well when compared with the results from the flowline model.
2. Volume–length (V-L) scaling
The procedure is analogous to (1) but the changes in the number of elevation bands, n, and the area are driven by the changes in glacier length which are calculated via volume–length scaling (Equation (9)). Thus, for year t + 1 the length is equal to:

Knowing the distance of each elevation band along the flowline and calculating the glacier length for each time-step of 1 year we derived the total number of elevation bands and the total glacier area from Equation (11). Thus the distribution of the new area with elevation was dictated by volume–length scaling instead of volume–area scaling. We adjusted the length according to V-L scaling, but kept the glacier’s width for each elevation band constant in time instead of adjusting it according to length–width scaling, thus allowing the scaling exponents in the V-A relationship (Equation (8)) to change in time.
3. Volume–area–length (V-A-L) scaling
We applied both Equations (13) and (14) in such a way that the number of bands, n, was calculated from V–L scaling while the changes in total area were derived from V–A scaling. This was achieved by assuming that the initial shape of the glacier area–elevation distribution remains constant in time (Fig. 5). A normalized area–elevation distribution is:

When multiplied by the calculated area, A(t), Equation (15) gives the area–elevation distribution for each year, t. As in the previous methods, the maximum altitude of the glacier remained constant. However, in contrast to the methods which assumed all area changes to occur exclusively at the glacier snout, V-A-L scaling removes or adds area along the entire length of the glacier. This approach may, in extreme cases, lead to an increase in the area of individual elevation bands although the glacier becomes shorter. It also decreases the area in the highest elevation bands of the glacier, where area would rarely change, especially for glaciers with large vertical extent and accumulation area. Nevertheless, this method is similar to the geometric model of Reference Raper, Brown and BraithwaiteRaper and others (2000) which has been used to estimate the contribution to sea-level rise from all mountain glaciers and ice caps (Reference Raper and BraithwaiteRaper and Braithwaite, 2006). Their geometric model calculates the terminus position from area–length scaling but approximates the area–altitude distribution with a triangle defined by maximum area at mean altitude and zero area at minimum and maximum altitude, while we preserve the actual shape of the initial area–elevation distribution through normalization of the distribution (Fig. 5).

Fig. 5. Modeled area–elevation distribution prior to future mass-balance perturbations (solid curve) and after 100 years of the mass-balance perturbations (dashed curve) for (a) Nigardsbreen and (b) Abramov Glacier.
Sensitivity experiments
Scaling parameters
Since we used γ = 1.375 and q = 2.2 in the scaling relationships, as proposed by Reference Bahr, Meier and PeckhamBahr and others (1997), we tested the sensitivity of glacier volume evolutions to the choice of γ and q by varying their values. For each experiment the constants of proportionality, c a and c l, were derived from the initial glacier volume, area and length for year t = 0, as obtained from the flowline model. Since these constants differ for each glacier, our second sensitivity experiment was to apply mean scaling constants, c a and c l, in the scaling methods and compare the derived volume evolutions with those produced by the flowline model.
Mass-balance/glacier-thickness feedback
Changes in mass balance cause changes in surface area and thickness with feedbacks on surface mass balance. We aimed to quantify the importance of the mass-balance/ thickness feedback both in the flowline model and in the scaling methods in comparison to the mass-balance feedback due to changes in area–elevation distribution. Since the ice-flow model is one-dimensional the changes in thickness along the flowline are assumed uniform across the width of the glacier. First we tested the importance of the massbalance/thickness feedback in the flowline model by excluding the thickness feedback mechanism from the projections. After the dynamical calibration had been finalized, the glacier thickness was kept constant for computation of the mass balance b(h, t).
The scaling methods applied here include feedback due to changes in area–elevation distribution, but lack the massbalance/thickness feedback, i.e. the glacier area may change, but the thickness along the glacier profile does not. A simple way of introducing this feedback into the scaling approach was to compute the mean glacier thickness, H m, for each year, t,

and derive the mean thickness change, ΔH, between two consecutive years. Assuming that the change in H m is equal to the change in thickness along the flowline, we calculated a surface profile, h(x), for year t) 1 by adding ΔH to the surface profile for year t. The surface profiles derived in this way for each t were used to calculate the mass-balance profile b(h, t) as a polynomial function of glacier surface elevation, h, along the flowline.
Results and Discussion
Scaling methods
Figure 6 illustrates the normalized volume evolutions (V(t) divided by V(0) for each year t) derived from the ice-flow model and the three scaling methods for all six glaciers. We show the evolutions derived only for Δb(0) = −0.015 m a−1, but the results in terms of differences from the flowline model are similar for all three mass-balance perturbations. In Table 2 we list the differences between the 100 year volume change projected by the flowline model and the scaling methods, given in percentages of the initial volume for all three perturbations. It must be borne in mind that the 1-D ice-flow model along the flowline of the glacier is highly parameterized and is a simplified representation of reality. For example, the model’s parameterizations may be introducing scaling relationships between the glacier’s characteristics that are inconsistent with those considered by Reference Bahr, Meier and PeckhamBahr and others (1997). Hence, the scaling exponents in the V-A and V-L relationships may differ from the theoretical scaling exponents. For example, valley glaciers will have scaling exponents γ = 1.375 and q = 2.2 if, among the other assumptions, the characteristic glacier width is linearly related to the characteristic glacier thickness (Reference BahrBahr, 1997b). This linearity may not result in the flowline model in the event that the combination of width parameterization (Equation (1)) and change in valley width, w s, along the flowline dictate the characteristic width–thickness scaling relationship. Nevertheless, the good agreement between model results and observations in the calibration period provides some confidence in the performance of the model.

Fig. 6. Future volume evolutions (normalized by initial volume at t = 0) for six glaciers, forced by a perturbation in mass-balance profile of Δb(0) = −0.015 m a−1, as projected from the flowline model (solid black curve), V–A scaling, V–L scaling and V–A–L scaling. The values for scaling constants, c a (m3−2γ ) and c l (m3−q ), derived from the glacier volume, area and length at t = 0, are specified for each glacier. The scaling exponents are assumed to be γ = 1.375 and q = 2.2 (Reference Bahr, Meier and PeckhamBahr and others, 1997).
Table 2. Differences between 100 year volume changes projected from the flowline model and those obtained from the scaling method (V–A, V–L, V–A–L, V–A(c a), V–L(c l) and V–L(h)) expressed in percentages (%) of the initial volume for each glacier. If the differences are positive (negative) the scaling method underestimates (overestimates) the volume loss projected from the flowline model. The projections are performed with three perturbations in mass-balance profile, Δb. In all cases the scaling exponents are equal to γ = 1.375 and q = 2.2 (Reference Bahr, Meier and PeckhamBahr and others, 1997) with the scaling constants given in Figure 6. V–A(c a) and V–L(c l) are the scaling methods with scaling constants equal to c a = 0.2055 m3−2γ (Reference Chen and OhmuraChen and Ohmura, 1990) and c l = 4.5507 m3−q . The column Vmod shows how much the volume loss projected by the flowline model differs from the flowline model results when the mass-balance/thickness feedback is excluded. V–L(h) shows the difference from the flowline model if the scheme for mass-balance/thickness feedback is included in the scaling method

All projections show considerable volume losses by the end of the 100 year period. As expected, the glaciers with more negative initial area-averaged mass balance, as calculated from the reference mass-balance profile, b ref (Table 1), lost a larger portion of their initial volume than those closer to zero mass balances. However, the scaling methods underestimate the total volume loss projected from the flowline model for most of the glaciers. This underestimation varies up to 47% (for Nigardsbreen, Δb(0) = −0.015 m a−1) for V-A scaling, up to 18% (for South Cascade, Δb(0) = −0.005 m a−1) for V-L scaling and up to 32% (for Abramov, Δb(0) = −0.005 m a−1) for V-A-L scaling. Part of the systematic underestimation by the scaling methods may be attributed to the initial state of the glaciers prior to the imposition of the mass-balance perturbations. Most of the glaciers experienced negative mass balances and were not in steady state prior to the perturbation. While the dynamic calibration of the ice model accounts for this non-steady state, scaling does not, since it includes no memory of the previous mass-balance history. Furthermore, while the dynamics in the ice-flow model are governed by Glen’s flow law, the scaling methods assume perfect plasticity, i.e. the assumption that dynamical changes in glacier geometry are instantaneous. As climate changes, the values of scaling constants, c a and c l, which we assume constant in time, may actually be expected to evolve with time as the glacier has to change its flow regime in response to resulting mass changes. Nevertheless, our results show that volume–length scaling gives the closest match to the evolutions from the flowline model. Thus, application of V-L scaling in order to derive the changes in area–elevation distribution which then dictate the volume change according to mass continuity (Equation (10)) is superior to V-A scaling when compared with normalized volume evolutions derived from the flowline model.
Since the width of the glacier in the flowline model is parameterized for each elevation band as a function of thickness (Equation (1)) the area in each elevation band is allowed to shrink or grow along the cross-section. However, the glacier length shrinks only when the thickness in the lowest elevation band reaches zero. Therefore, the flowline model allows the glacier to have a thin terminus with a relatively large terminus area. Considering these characteristics of the flowline model, the lower performance of V-A and V-A-L scaling compared with V-L scaling is attributed to the following considerations:
In V-A and V-L scaling, changes in surface area occur only at the glacier snout. However, in the V-A scaling the lost area (ΔA) is subtracted from the glacier front along the flowline, reducing the length of the glacier, i.e. removing the lower-lying elevation bands which have the most negative specific mass balance (ablation area). Since this removal of low-lying area occurs faster than in the flowline model and in V-L scaling, it leads to less-negative mass balance when integrated over the entire glacier (Equation (10)), and hence, to reduced volume losses with time. Integrating over 100 years, the projected volume change becomes progressively less in comparison with V-L scaling and with the flowline model.
By applying V-A-L scaling we allow for area changes to occur along the entire glacier length. Glacier retreat is simulated by V-L scaling while the total area is calculated from the V-A scaling. Since the shape of the area–elevation distribution is preserved (Fig. 5), a certain amount of area is lost in each elevation band along the flowline. This means that V-A-L cannot simulate the maximum reduction of the thickness and area at the glacier terminus as it occurs in the flowline model. Since the volume changes in V-A-L are computed with consistently smaller areas in elevation bands than in the flowline model the V-A-L scaling underestimates the modeled volume loss (Equation (10)) over the 100 year period compared with the flowline model.
Although the projected 100 year volume did not differ more than a few percent, depending on whether the V-A or V-A-L scaling method was applied, the performance of these methods depends on the glacier’s area–elevation distribution. Therefore, for Nigardsbreen, a glacier with a long narrow tongue (Fig. 5) and large accumulation area, the V-A scaling yielded the largest underestimate of the volume loss compared with the flow model results. As the physical basis for the scaling relationships is explained for valley glaciers (Reference Bahr, Meier and PeckhamBahr and others, 1997), Nigardsbreen, as an outlet glacier of Jostedalsbreen, is not a representative valley glacier but more an outlier in our sample. Another glacier for which the scaling methods gave large differences from the flowline model is South Cascade Glacier. This might be due to problems we encountered during the dynamical calibration for this glacier, yielding the future projections to be highly sensitive to the tuning parameters in the flowline model.
Sensitivity to scaling exponents
The first sensitivity experiment involved varying the scaling exponents, γ and q, in the V-A and V-L relationships for our six glaciers to analyze the sensitivity of volume evolutions to these scaling exponents. We investigated how much the scaling exponents can be decreased (increased) so that the scaling methods project 100 year volume changes that are 10% and 20% smaller (larger) than the ‘reference’ volume change. Here, the’reference’volume projections are those derived from the scaling method with γ = 1.375 and q = 2.2, as proposed by Reference Bahr, Meier and PeckhamBahr and others (1997). Reducing γ in the V-A scaling to γ = 0.95 or increasing it to γ = 2.00 underestimates and overestimates, respectively, the reference loss by <10%. Further decrease to γ = 0.65 and increase to γ = 2.95 results in projections of volume loss that are within 20% of the volume loss projected by the ‘reference’ scaling.
For V-L scaling, assuming 1.52 ≤ q ≤ 3.20 results in volume projections that differ from the ‘reference’ volume change by <10%. The range is 1.04 ≤ q ≤ 4.72 if a 20% difference is tolerated. Additionally, the results show that the volume evolutions for glaciers that lost almost their entire volume over the 100 year period (South Cascade Glacier, midre Lovénbreen and Abramov glacier) are more sensitive to variations in the scaling exponents than those for the other glaciers in our sample.
Our sensitivity experiments show that by decreasing the scaling exponents γ and q by 30% (50%) or increasing them by 45% (110%) from the theoretically derived values by Reference Bahr, Meier and PeckhamBahr and others (1997) the projections of 100 year volume change differ by <10% (<20%). Applying the range γ = [1.15 1.52], which was reported by Reference Chen and OhmuraChen and Ohmura (1990), we derive 100 year volume projections which differ <5% from the ‘reference’ projections. Similar analysis performed on synthetic glaciers with V-A scaling (Reference Radić, Hock and OerlemansRadić and others, 2007) showed that the range of γ from 1.80 to 2.90 in V-A scaling yielded differences of <6% in 100 year volume changes derived from the V-A scaling with γ = 1.56. Hence, we conclude that the normalized volume evolutions are relatively insensitive to the choice of scaling exponents. However, one should note that the scaling relationships, especially V-A scaling, will be affected if the geometry parameterizations in the ice-flow model have large inconsistencies with the geometry of valley glaciers considered by Reference Bahr, Meier and PeckhamBahr and others (1997).
Sensitivity to scaling constants
So far we have calculated c a and c l (Equations (8) and (9)) from the initial volume, area and length for each glacier assuming γ = 1.375 and q = 2.2. In Figure 6 we present the values of these constants. Reference Chen and OhmuraChen and Ohmura (1990) found c a = 0.2055 m3−2γ and Reference Raper and BraithwaiteRaper and Braithwaite (2006) applied their value for assessing global glacier wastages.
For comparison we apply the constant c a from Reference Chen and OhmuraChen and Ohmura (1990) to derive volume evolutions based on V-A scaling. Since values for the constant in V-L scaling, c l, could not be found in the literature, we use the mean c l calculated from our six glaciers (c l = 4.5507 m3−q ). When these constants are used to calculate initial volume, at t = 0, from Equations (8) and (9), initial volume differs from the modeled volumes by up to 57% for V-A scaling and by up to 35% for V-L scaling. This supports the statement by Reference MeierMeier and others (2007) that the error in calculating volumes from areas using V-A scaling is ∼50% for individual ice masses. However the 100 year volume projections derived from the scaling methods show a scatter of underestimation and overestimation from the projections derived by the flowline model (Fig. 7). Statistically this scatter might reduce the errors in total volume projections if the scaling is applied to a large sample of glaciers (e.g. on a global scale). However, quantification of errors is difficult since it depends on how any particular glacier fits into the V-A scaling with an assumed constant, c a.

Fig. 7. Same as Figure 6, except that absolute volumes are shown and scaling constant c a = 0.2055 m3−2γ (Reference Chen and OhmuraChen and Ohmura, 1990) and c l = 4.5507 m3−q are used.
Even though initial volumes are both under- and overestimated (Fig. 7), when normalized, V-A scaling consistently underestimates the glacier wastage at the end of the 100 year projection by 9%–59% (Table 2) compared with the flowline model, while V-L yields a slight underestimate or a close match (Fig. 8). Applying the scaling constant c l averaged over all glaciers in the V-L scaling yields projected 100 year volume changes that are only in the order of a few percent different from the projections using c l derived for each glacier individually. Hence, the results are rather insensitive to the choice of c l, which is encouraging for the use of V-L scaling in glacier-volume projections, especially combined with the finding of generally good performance of the method when compared with the ice-flow model projections.

Fig. 8. Same as Figure 7, except that volumes are normalized by initial volumes at t = 0.
When deriving scaling constants c l and c a from values of V, A and L, one should keep in mind that the scaling constants are related through Equations (8) and (9) by:
Hence, varying c a by a certain amount is equivalent to varying c l by a much larger amount since (Aγ /Lq ) is of the order of magnitude 10–1000. If this is not considered it will appear that c l is ∼10–1000 less sensitive than c a.
Mass-balance/thickness feedback
Our final sensitivity experiment is to analyze the importance of mass-balance/thickness feedback. When the changes in glacier thickness along the flowline are excluded from the mass-balance calculations in the flowline model, the projected 100 year volume loss is underestimated (Table 2). According to our results, the feedback mechanism in the flowline model contributes to the volume loss 2–14% of the initial volume while the glacier loses 50–100% of its volume. Thus the mass-balance/thickness feedback is small for these six glaciers. However, the importance of this feedback depends strongly on the bed slope (Reference OerlemansOerlemans, 2001). Therefore, this analysis may yield different results if applied to large glaciers which lie on much smaller slopes.
We next include our simple feedback scheme in the scaling methods to test whether this can improve the match between the volume evolutions derived from the scaling methods and the flowline model. The differences in the projected volumes between the flowline model and the V-L scaling method are listed in Table 2. Our simple mechanism in the V-L scaling method increases the glacier’s wastage but not more than a few percent. When the feedback mechanism is introduced in the V-A and V-A-L scaling the wastage is increased even less (<1% of the initial volume).
Our approach must be considered as a first approximation since the glacier thickness change is assumed uniform over the profile (Equation (16)). One might apply a more complex scheme of thickness change, for example by parameterizing the thickness change along the flowline (Reference Jóhannesson, Raymond and WaddingtonJóhannesson and others, 1989). Such a parameterization takes into account that the change in the ice thickness is not uniformly distributed but is more pronounced at the glacier tongue. However, in order to derive volume evolution from the discretized mass continuity (Equation (10)) it would require thickness data along the flowline. Since we analyze the scaling methods which are applicable for global estimates, simplicity in the data input is more important than the complexity of the feedback scheme. Considering that the mass-balance/thickness feedback is small for these six glaciers, the V-L scaling is shown to simulate sufficiently well the feedback between the mass balance and area change as simulated in the flowline model.
Conclusions
We provide a detailed analysis of scaling methods as a possible tool for deriving glacier-volume evolutions on a global scale. Using 100 year volume evolutions from the flowline model as a reference, we compare the performance of three different scaling methods for six valley glaciers, assuming identical hypothetical trend-like negative mass-balance perturbations of −0.005, −0.010 and −0.015 m a−1. For all six glaciers, the scaling methods mostly underestimate the 100 year normalized volume losses obtained from the flowline model. Nevertheless, the volume evolutions derived from the volume–length (V-L) scaling provide the best match to the evolutions derived from the flowline model. This scaling method projects volume loss by the end of a 100 year period deviating up to 18% of initial volume from the modeled projections, while volume–area (V-A) and volume–area–length (V-A-L) produced maximum differences of 47% and 32%, respectively. Thus the underestimate of the total volume loss is ∼20% larger if V-A scaling is applied instead of V-L scaling. Although both the V-A and V-L scaling are derived from the exact same continuum mechanics, our results suggest that V-L scaling may be a better practical tool for assessing future volume changes. However, more glaciers need to be analyzed to confirm these results, especially considering that our six glaciers are small and, hence, not a representative sample of the mountain glaciers and ice caps that are major contributors to sea level (e.g. Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002; Reference Rignot, Rivera and CasassaRignot and others, 2003). Lack of data is a major obstacle for extending this sensitivity analysis to large glacier systems and ice caps. Additionally, the validity of scaling methods should be further investigated by comparing their performance with 2-D and 3-D ice-flow models which account for cross-sectional thickness and geometry changes in a more sophisticated way.
Although the application of V-L scaling in modeling volume changes seems to be more accurate than V-A scaling, it might be less practical, since gathering glacier area data is relatively simple while gathering data for glacier length along the flowline is more difficult. Nevertheless, the potential application of V-L scaling combined with the use of glacier length records in extracting past temperature variations on a century timescale (Reference OerlemansOerlemans, 2005) emphasizes the need to continue or expand monitoring of glacier length fluctuations. V-L scaling has also been applied in reconstructing the historical glacier contribution to sea-level rise (Reference Oerlemans, Dyurgerov and van de WalOerlemans and others, 2007).
As expected, initial volumes and volumes of 100 year projections of individual glaciers are highly sensitive to the choice of the scaling constants, especially in V-A scaling, yielding both over- and underestimation of volumes. However, when normalized by initial volume, volume evolutions are relatively insensitive to the choice of scaling exponents and constants. Varying γ = 1.375 and q = 2.2 (Reference Bahr, Meier and PeckhamBahr and others, 1997) by −30% (−50%) and +45% (+110%) yields a difference in 100 year volume projections of less than ±10% (±20%). This is encouraging for the use of scaling methods in global volume projections, since scaling constants are unknown for most glaciers and the scaling exponents may vary with changing glacier geometry.
Acknowledgements
Financial support for this work was provided by the Swedish Research Council for Environment, Agricultural Sciences and Spatial Planning (project No. 21.4/2003-0387). R. Hock is a Royal Swedish Academy of Science Research Fellow, supported by a grant from the Knut Wallenberg Foundation. We are grateful to R. van de Wal and B. De Smedt for providing the input geometry data needed for the flowline model of Nigardsbreen and Sofiyskiy glacier. We thank W.R. Bidlake and I. Willis for providing digitized data of surface and bed topography for South Cascade Glacier and midre Lovénbreen. We are grateful to L.A. Rasmussen for the information on historical fluctuations of South Cascade Glacier and to L.N. Braun for providing the surface and bed topography maps of Abramov glacier. Comments by W.D. Harrison, L.A. Rasmussen, A.A. Arendt, M. Truffer and M. de Woul have helped to improve the paper. Special thanks to Scientific Editor H. Rott and to A. Fountain and D.B. Bahr whose helpful reviews clarified many points in the text.












