1 Introduction
A list
${\mathit{ys}}$
is said to be an immediate sublist of
${\mathit{xs}}$
if
${\mathit{ys}}$
can be obtained by removing exactly one element from
${\mathit{xs}}$
. For example, the four immediate sublists of
${\mathtt{"abcd"}}$
are
${\mathtt{"abc"}}$
,
${\mathtt{"abd"}}$
,
${\mathtt{"acd"}}$
, and
${\mathtt{"bcd"}}$
. Consider computing a function
${\mathit{h}}$
that takes a list as input, with the property that the value of
${\mathit{h}\;\mathit{xs}}$
depends on values of
${\mathit{h}}$
at all the immediate sublists of
${\mathit{xs}}$
. For example, as seen in Figure 1,
${\mathit{h}\;\mathtt{"abcd"}}$
depends on
${\mathit{h}\;\mathtt{"abc"}}$
,
${\mathit{h}\;\mathtt{"abd"}}$
,
${\mathit{h}\;\mathtt{"acd"}}$
, and
${\mathit{h}\;\mathtt{"bcd"}}$
. In this top-down manner, to compute
${\mathit{h}\;\mathtt{"abc"}}$
, we make calls to
${\mathit{h}\;\mathtt{"ab"}}$
,
${\mathit{h}\;\mathtt{"ac"}}$
, and
${\mathit{h}\;\mathtt{"bc"}}$
; to compute
${\mathit{h}\;\mathtt{"abd"}}$
, we make a call to
${\mathit{h}\;\mathtt{"ab"}}$
as well—many values end up being re-computed. One would like to instead proceed in a bottom-up manner, storing computed values so that they can be reused. For this problem, one might want to build a lattice-like structure, like that in Figure 2, from bottom to top, such that each level reuses values computed in the level below it.
Fig. 1. Computing
${\mathit{h}\;\mathtt{"abcd"}}$
top-down. String constants are shown using monospace font but without quotes, to save space.
Fig. 2. Computing
${\mathit{h}\;\mathtt{"abcde"}}$
bottom-up. The numbers on the left denote the levels.
Bird (Reference Bird2008) presented a study of the relationship between top-down and bottom-up algorithms. It was shown that if an algorithm can be written in a specific top-down style, with ingredients that satisfy certain properties, there is an equivalent bottom-up algorithm that stores intermediate results in a table. The “all immediate sublists” instance was the last example of the paper. To tackle the problem, however, Bird had to introduce, out of the blue, a binary tree and a concise but cryptic four-line function. The tree appears to obey some shape constraints, but that was not explicitly stated. Regarding the four-line function, which lies at the core of the bottom-up algorithm, we know from its type that it turns a tree into a tree of lists, and that is probably all one can say with confidence. Not only is it hard to see what the function exactly does, it is even not easy to see why the function, involving use of partial operations such as zipping trees of the same shape, always succeeds. Given limited space, Bird did not offer much rationale or explanation, nor did he prove that the function satisfies the said properties that should be met by a bottom-up algorithm.
The author finds this algorithm fascinating and struggled to understand it. As Bird would agree, a good way to understand an algorithm is to calculate it; thus, this pearl came into being. In this pearl, we review this problem, reveal a connection between “
${\mathit{n}}$
choose
${\mathit{k}}$
” and “
${\mathit{n}}$
choose
${\mathrm{1}\mathbin{+}\mathit{k}}$
” that was not explicit in Bird (Reference Bird2008), motivate the introduction of the tree, and finally construct a formal specification of the four-line function (which we call
${\mathit{up}}$
in this pearl). Once we have a specification,
${\mathit{up}}$
can be calculated—not without some tricky eureka that made the calculation fun. It then turns out that there is a formula describing the role of
${\mathit{up}}$
in the bottom-up algorithm that is different and simpler than that in Bird (Reference Bird2008).
One might ask: are there actually such problems, whose solution of input
${\mathit{xs}}$
depends on solutions of immediate sublists of
${\mathit{xs}}$
? It turns out that it is well known in the algorithm community that, while problems such as minimum edit distance or longest common subsequence are defined on two lists, with clever encoding, they can be rephrased as problems defined on one list whose solution depends on immediate sublists. Many problems in additive combinatorics (Tao & Vu, Reference Tao and Vu2012) can also be cast into this form.
But those are just bonuses. The application of a puzzle is being solved, a good puzzle is one that is fun to solve, and a functional pearl is a story about solving a puzzle. One sees a problem, wonders whether there is an elegant solution, finds the right specification, tries to calculate it, encounters some head-scratching moments and surprising twists alone the way, but eventually overcomes the obstacle and comes up with a concise and beautiful algorithm. One then writes about the adventure, to share the fun.
2 Specification
We use a Haskell-like notation throughout the paper. Like in Haskell, if a function is defined by multiple clauses, the patterns and guards are matched in the order they appear. Differences from Haskell include that we allow
${\mathit{n}\mathbin{+}\mathit{k}}$
pattern, and that we denote the type of list by
${\mathsf{L}}$
, equipped with its
${\mathit{map}}$
function
${\mathit{map}\mathbin{::}(\mathit{a}\to \mathit{b})\to \mathsf{L}\;\mathit{a}\to \mathsf{L}\;\mathit{b}}$
.
The immediate sublists of a list can be specified in many ways. We use the definition below because it allows the proofs of this pearl to proceed in terms of cons-lists, which is familiar to most readers, while it also generates sublists in an order that is more intuitive:
For example,
${\mathit{subs}\;\mathtt{"abcde"}}$
yields
${[ \mathtt{"abcd"},\mathtt{"abce"},\mathtt{"abde"},\mathtt{"acde"},\mathtt{"bcde"}]}$
.
Denote the function we wish to compute by
${\mathit{h}\mathbin{::}\mathsf{L}\;\mathsf{X}\to \mathsf{Y}}$
for some types
${\mathsf{X}}$
and
${\mathsf{Y}}$
. We assume that it is a partial function defined on non-empty lists and can be computed top-down as below:
where
${\mathit{f}\mathbin{::}\mathsf{X}\to \mathsf{Y}}$
is used in the base case when the input is a singleton list, and
${\mathit{g}\mathbin{::}\mathsf{L}\;\mathsf{Y}\to \mathsf{Y}}$
is for the inductive case.
For this pearl, it is convenient to use an equivalent definition. Let
${\mathit{td}}$
(referring to “top-down”) be a family of functions indexed by natural numbers (denoted by
${\mathsf{Nat}}$
):
Here, the function
${\mathit{ex}\mathbin{::}\mathsf{L}\;\mathit{a}\to \mathit{a}}$
takes a singleton list and extracts the only component. The intention is that
${\mathit{td}\;\mathit{n}}$
is a function defined on lists of length exactly
${\mathrm{1}\mathbin{+}\mathit{n}}$
. The call
${\mathit{td}\;\mathit{n}}$
in the body of
${\mathit{td}\;(\mathrm{1}\mathbin{+}\mathit{n})}$
is defined because
${\mathit{subs}}$
, given an input of length
${\mathrm{1}\mathbin{+}\mathit{n}}$
, returns lists of length
${\mathit{n}}$
. Given input
${\mathit{xs}}$
, the value we aim to compute is
${\mathit{h}\;\mathit{xs}\mathrel{=}\mathit{td}\;(\mathit{length}\;\mathit{xs}\mathbin{-}\mathrm{1})\;\mathit{xs}}$
.
The function
${\mathit{repeat}\;\mathit{k}}$
composes a function with itself
${\mathit{k}}$
times:
For brevity, we will write
${\mathit{repeat}\;\mathit{k}\;\mathit{f}}$
as
${{\mathit{f}}^{\mathit{k}}}$
for the rest of this pearl. We aim to construct a bottom-up algorithm having the following form:
where
${\mathit{pre}}$
preprocesses the input and builds the lowest level in Figure 2, and each
${\mathit{step}}$
builds a level from the one below. For input of length
${\mathrm{1}\mathbin{+}\mathit{n}}$
, we repeat
${\mathit{n}}$
times and, by then, we can extract the singleton value by
${\mathit{post}}$
.
Our aim is to construct
${\mathit{pre}}$
,
${\mathit{step}}$
, and
${\mathit{post}}$
such that
${\mathit{td}\mathrel{=}\mathit{bu}}$
.
3 Building a new level
To find out what
${\mathit{step}}$
might be, we need to figure out how to specify a level, and what happens when a level is built from the one below it. We use Figure 2 as our motivating example. As one can see, level
${\mathrm{2}}$
in Figure 2 consists of sublists of
${\mathtt{"abcde"}}$
that have length
${\mathrm{2}}$
, and level
${\mathrm{3}}$
consists of sublists having length
${\mathrm{3}}$
, etc. Let
${\mathit{choose}\;\mathit{k}\;\mathit{xs}}$
denote choosing
${\mathit{k}}$
elements from the list
${\mathit{xs}}$
:
Its definition follows basic combinatorics: the only way to choose
${\mathrm{0}}$
elements from a list is
${[ ]};$
if
${\mathit{length}\;\mathit{xs}\mathrel{=}\mathit{k}}$
, the only way to choose
${\mathit{k}}$
elements is
${\mathit{xs}}$
. Otherwise, to choose
${\mathrm{1}\mathbin{+}\mathit{k}}$
elements from
${\mathit{x}\mathbin{:}\mathit{xs}}$
, one can either keep
${\mathit{x}}$
and choose
${\mathit{k}}$
from
${\mathit{xs}}$
, or choose
${\mathrm{1}\mathbin{+}\mathit{k}}$
elements from
${\mathit{xs}}$
. For example,
${\mathit{choose}\;\mathrm{3}\;\mathtt{"abcde"}}$
yields
${[ \mathtt{"abc"},\mathtt{"abd"},\mathtt{"abe"},\mathtt{"acd"},\mathtt{"ace"},\mathtt{"ade"},\mathtt{"bcd"},\mathtt{"bce"},\mathtt{"bde"},\mathtt{"cde"}]}$
. Note that
${\mathit{choose}\;\mathit{k}\;\mathit{xs}}$
is defined only when
${\mathit{k}\leq \mathit{length}\;\mathit{xs}}$
.
If the levels in Figure 2 were to be represented as lists, each level
${\mathit{k}}$
is given by
${\mathit{map}\;\mathit{h}\;(\mathit{choose}\;\mathit{k}\;\mathit{xs})}$
. For example, level
${\mathrm{2}}$
in Figure 2 is (string literals are shown in typewriter font; double quotes are omitted to reduce noise in the presentation):
To build level
${\mathrm{3}}$
from level
${\mathrm{2}}$
, we wish to have a function
${\mathit{upgrade}\mathbin{::}\mathsf{L}\;\mathsf{Y}\to \mathsf{L}\;(\mathsf{L}\;\mathsf{Y})}$
that is able to somehow bring together the relevant entries from level
${\mathrm{2}}$
:
With
${[ \mathit{h}\;\mathtt{ab},\mathit{h}\;\mathtt{ac},\mathit{h}\;\mathtt{bc}]}$
one can compute
${\mathit{h}\;\mathtt{abc}}$
, and with
${[ \mathit{h}\;\mathtt{ab},\mathit{h}\;\mathtt{ad},\mathit{h}\;\mathtt{bd}]}$
one can compute
${\mathit{h}\;\mathtt{abd}}$
, etc. That is, if we apply
${\mathit{map}\;\mathit{g}}$
to the result of
${\mathit{upgrade}}$
above, we get
which is level
${\mathrm{3}}$
, or
${\mathit{map}\;\mathit{h}\;(\mathit{choose}\;\mathrm{3}\;\mathtt{abcde})}$
. The function
${\mathit{upgrade}}$
need not inspect the values of each element, but rearrange them by position—it is a natural transformation
${\mathsf{L}\;\mathit{a}\to \mathsf{L}\;(\mathsf{L}\;\mathit{a})}$
. As far as
${\mathit{upgrade}}$
is concerned, it does not matter whether
${\mathit{h}}$
is applied or not. Letting
${\mathit{h}\mathrel{=}\mathit{id}}$
, observe that
${\mathit{upgrade}\;(\mathit{choose}\;\mathrm{2}\;\mathtt{abcde})\mathrel{=}}$
${[ [ \mathtt{ab},\mathtt{ac},\mathtt{bc}],[ \mathtt{ab},\mathtt{ad},\mathtt{bd}]\mathbin{...}]}$
and
${\mathit{choose}\;\mathrm{3}\;\mathtt{abcde}\mathrel{=}}$
${[ \mathtt{abc},\mathtt{abd},\mathtt{abe},\mathtt{acd}\mathbin{...}]}$
are related by
${\mathit{map}\;\mathit{subs}}$
. Each
${\mathit{step}}$
we perform in the bottom-up algorithm could be
${\mathit{map}\;\mathit{g}\, {\circ} \,\mathit{upgrade}}$
.
Formalizing the observations above, we want
${\mathit{upgrade}\mathbin{::}\mathsf{L}\;\mathit{a}\to \mathsf{L}\;(\mathsf{L}\;\mathit{a})}$
to satisfy:
Given (3.1), we may let each step in the bottom-up algorithm be
${\mathit{map}\;\mathit{g} \, \, {\circ} \, \, \mathit{upgrade}}$
.
Equation (3.1) is a specification of
${\mathit{upgrade}}$
, constructed by observation and generalization. We want it to serve two purposes: 1. we wish to calculate from it a definition of
${\mathit{upgrade}}$
, and 2. it plays a central role in proving that the bottom-up algorithm, also to be constructed, equals the top-down algorithm. That (3.1) (in fact, a stronger version of it) does meet the purposes above will be formally justified later. For now, we try to gain some intuition by demonstrating below that, with (3.1) satisfied,
${\mathit{map}\;\mathit{g} \, {\circ} \, \mathit{upgrade}}$
builds level
${\mathit{k}\mathbin{+}\mathrm{1}}$
from level
${\mathit{k}}$
. Let the input be
${\mathit{xs}}$
. If
${\mathit{xs}}$
is a singleton list, the bottom-up algorithm has finished, so we consider
${\mathit{xs}}$
having length at least
${\mathrm{2}}$
. Recall that level
${\mathit{k}}$
is
${\mathit{map}\;\mathit{h}\;(\mathit{choose}\;\mathit{k}\;\mathit{xs})}$
. Applying
${\mathit{map}\;\mathit{g} \, \, {\circ} \, \, \mathit{upgrade}}$
to level
${\mathit{k}}$
:
We get level
${\mathrm{1}\mathbin{+}\mathit{k}}$
.
The constraints on
${\mathit{k}}$
in (3.1) may need some explanation. For
${\mathit{choose}\;(\mathrm{1}\mathbin{+}\mathit{k})\;\mathit{xs}}$
on the RHS to be defined, we need
${\mathrm{1}\mathbin{+}\mathit{k}\leq \mathit{length}\;\mathit{xs}}$
. Meanwhile, no
${\mathit{upgrade}}$
could satisfy (3.1) when
${\mathit{k}\mathrel{=}\mathrm{0}}$
: on the LHS,
${\mathit{upgrade}}$
cannot distinguish between
${\mathit{choose}\;\mathrm{0}\;\mathtt{ab}}$
and
${\mathit{choose}\;\mathrm{0}\;\mathtt{abc}}$
, both evaluating to [ [ ]], while on the RHS
${\mathit{choose}\;\mathrm{1}\;\mathtt{ab}}$
and
${\mathit{choose}\;\mathrm{1}\;\mathtt{abc}}$
have different shapes. Therefore, we only demand (3.1) to hold when
${\mathrm{1}\leq \mathit{k}}$
, which is sufficient because we only apply
${\mathit{upgrade}}$
to level
${\mathrm{1}}$
and above. Together, the constraint is
${\mathrm{2}\leq \mathrm{1}\mathbin{+}\mathit{k}\leq \mathit{length}\;\mathit{xs}}$
—
${\mathit{xs}}$
should have at least
${\mathrm{2}}$
elements.
Can we construct such an
${\mathit{upgrade}}$
?
4 Building levels represented by trees
We may proceed with (3.1) and construct
${\mathit{upgrade}}$
. We will soon meet a small obstacle: in an inductive case
${\mathit{upgrade}}$
will receive a list computed by
${\mathit{choose}\;(\mathrm{1}\mathbin{+}\mathit{k})\;(\mathit{x}\mathbin{:}\mathit{xs})}$
, that is,
${\mathit{map}\;(\mathit{x}\mathbin{:})\;(\mathit{choose}\;\mathit{k}\;\mathit{xs})}$
and
${\mathit{choose}\;(\mathrm{1}\mathbin{+}\mathit{k})\;\mathit{xs}}$
concatenated by
${(\mathbin{{+}\mskip-8mu{+}})}$
, and split it back to the two lists. This can be done, but it is rather tedious. This is a hint that some useful information has been lost when we represent levels by lists. To make the job of
${\mathit{upgrade}}$
easier, we switch to a more informative data structure.
4.1 Binomial trees
Instead of lists, we define the following tip-valued binary tree:
We assume that
${\mathsf{B}}$
is equipped with two functions derivable from its definition:
The function
${\mathit{mapB}\;\mathit{f}}$
applies
${\mathit{f}}$
to every tip of the given tree. Given two trees
${\mathit{t}}$
and
${\mathit{u}}$
having the same shape,
${\mathit{zipBW}\;\mathit{f}\;\mathit{t}\;\mathit{u}}$
“zips” the trees together, applying
${\mathit{f}}$
to values on the tips—the name stands for “zip
${\mathsf{B}}$
-trees with”. If
${\mathit{t}}$
and
${\mathit{u}}$
have different shapes,
${\mathit{zipBW}\;\mathit{f}\;\mathit{t}\;\mathit{u}}$
is undefined. Furthermore, for the purpose of specification we assume a function
${\mathit{flatten}\mathbin{::}\mathsf{B}\;\mathit{a}\to \mathsf{L}\;\mathit{a}}$
that “flattens” a tree to a list by collecting all the values on the tips left-to-right.
Having
${\mathsf{B}}$
allows us to define an alternative to
${\mathit{choose}}$
:
The function
${\mathit{ch}}$
resembles
${\mathit{choose}}$
. In the first two clauses,
${\mathsf{T}}$
corresponds to a singleton list. In the last clause,
${\mathit{ch}}$
is like
${\mathit{choose}}$
but, instead of appending the results of the two recursive calls, we store the results in the two branches of the binary tree, thus recording how the choices were made: if
${\mathit{ch}\;\_ \;(\mathit{x}\mathbin{:}\mathit{xs})\mathrel{=}\mathsf{N}\;\mathit{t}\;\mathit{u}}$
, the subtree
${\mathit{t}}$
contains all the tips with
${\mathit{x}}$
chosen, while
${\mathit{u}}$
contains all the tips with
${\mathit{x}}$
discarded. See Figure 3 for some examples. We have
${\mathit{flatten}\;(\mathit{ch}\;\mathit{k}\;\mathit{xs})\mathrel{=}\mathit{choose}\;\mathit{k}\;\mathit{xs}}$
, that is,
${\mathit{choose}}$
forgets the information retained by
${\mathit{ch}}$
.
Fig. 3. Results of
${\mathit{ch}}$
.
The counterpart of
${\mathit{upgrade}}$
on trees, which we will call
${\mathit{up}}$
, will be a natural transformation of type
${\mathsf{B}\;\mathit{a}\to \mathsf{B}\;(\mathsf{L}\;\mathit{a})}$
. Its relationship to
${\mathit{upgrade}}$
is given by
${\mathit{flatten}\;(\mathit{up}\;(\mathit{ch}\;\mathit{k}\;\mathit{xs}))\mathrel{=}\mathit{upgrade}\;(\mathit{choose}\;\mathit{k}\;\mathit{xs})}$
. The function
${\mathit{up}}$
should satisfy the following specification:
It is a stronger version of (3.1)–(4.1) reduces to (3.1) if we apply
${\mathit{flatten}}$
to both sides.
Now we are ready to derive
${\mathit{up}}$
.
4.2 The derivation
The derivation proceeds by trying to construct a proof of (4.1) and, when stuck, pausing to think about how
${\mathit{up}}$
should be defined to allow the proof to go through. That is, the definition of
${\mathit{up}}$
and a proof that it satisfies (4.1) are developed hand-in-hand.
The proof, if constructed, will be an induction on
${\mathit{xs}}$
. The case analysis follows the shape of
${\mathit{ch}\;(\mathrm{1}\mathbin{+}\mathit{k})\;\mathit{xs}}$
(on the RHS of (4.1)). Therefore, there is a base case, a case when
${\mathit{xs}}$
is non-empty and
${\mathrm{1}\mathbin{+}\mathit{k}\mathrel{=}\mathit{length}\;\mathit{xs}}$
, and a case when
${\mathrm{1}\mathbin{+}\mathit{k}\mathbin{<}\mathit{length}\;\mathit{xs}}$
. However, since the constraints demand that
${\mathit{xs}}$
has at least two elements, the base case will be lists of length
${\mathrm{2}}$
, and in the inductive cases the length of the list will be at least
${\mathrm{3}}$
.
Case 1.
${\mathit{xs}\mathbin{:=}[ \mathit{y},\mathit{z}]}$
.Footnote
1
The constraints force
${\mathit{k}}$
to be
${\mathrm{1}}$
. We simplify the RHS of (4.1):
Now consider the LHS:
The two sides can be made equal if we let
${\mathit{up}\;(\mathsf{N}\;(\mathsf{T}\;\mathit{p})\;(\mathsf{T}\;\mathit{q}))\mathrel{=}\mathsf{T}\;[ \mathit{p},\mathit{q}]}$
.
Case 2.
${\mathit{xs}\mathbin{:=}\mathit{x}\mathbin{:}\mathit{xs}}$
where
${\mathit{length}\;\mathit{xs}\geq \mathrm{2}}$
, and
${\mathrm{1}\mathbin{+}\mathit{k}\mathrel{=}\mathit{length}\;(\mathit{x}\mathbin{:}\mathit{xs})}$
.
We leave details of this case to the readers as an exercise, since we would prefer giving more attention to the next case. For this case, we will construct
In this case,
${\mathit{up}\;\mathit{t}}$
always returns a
${\mathsf{T}}$
. The function
${\mathit{unT}\;(\mathsf{T}\;\mathit{p})\mathrel{=}\mathit{p}}$
removes the constructor and exposes the list it contains. While the correctness of this case is established by the constructed proof, a complementary explanation why
${\mathit{up}\;\mathit{t}}$
always returns a singleton tree and thus
${\mathit{unT}}$
always succeeds is given in Section 4.3.
Case 3.
${\mathit{xs}\mathbin{:=}\mathit{x}\mathbin{:}\mathit{xs}}$
,
${\mathit{k}\mathbin{:=}\mathrm{1}\mathbin{+}\mathit{k}}$
, where
${\mathit{length}\;\mathit{xs}\geq \mathrm{2}}$
, and
${\mathrm{1}\mathbin{+}(\mathrm{1}\mathbin{+}\mathit{k})\mathbin{<}\mathit{length}\;(\mathit{x}\mathbin{:}\mathit{xs})}$
.
The constraints become
${\mathrm{2}\leq \mathrm{2}\mathbin{+}\mathit{k}\mathbin{<}\mathit{length}\;(\mathit{x}\mathbin{:}\mathit{xs})}$
. Again we start with the RHS and try to reach the LHS:
Note that the induction step is valid because we are performing induction on
${\mathit{xs}}$
, and thus
${\mathit{k}}$
in (4.1) is universally quantified. We now look at the LHS:
Expressions (4.2) and (4.3) can be unified if we define
The missing part
${\mathbin{???}}$
shall be an expression that is allowed to use only the two subtrees
${\mathit{t}}$
and
${\mathit{u}}$
that
${\mathit{up}}$
receives. Given
${\mathit{t}\mathrel{=}\mathit{mapB}\;(\mathit{x}\mathbin{:})\;(\mathit{ch}\;\mathit{k}\;\mathit{xs})}$
and
${\mathit{u}\mathrel{=}\mathit{ch}\;(\mathrm{1}\mathbin{+}\mathit{k})\;\mathit{xs}}$
(from (4.3)), this expression shall evaluate to the subexpression in (4.2) (let us call it (4.2.1)):
It may appear that, now that
${\mathit{up}}$
already has
${\mathit{u}\mathrel{=}\mathit{ch}\;(\mathrm{1}\mathbin{+}\mathit{k})\;\mathit{xs}}$
, the
${\mathbin{???}}$
may simply be
${\mathit{mapB}\;(\mathit{subs}\, {\circ} \,(\mathit{x}\mathbin{:}))\;\mathit{u}}$
. The problem is that the
${\mathit{up}}$
does not know what
${\mathit{x}}$
is—unless
${\mathit{k}\mathrel{=}\mathrm{0}}$
.
Case 3.1.
${\mathit{k}\mathrel{=}\mathrm{0}}$
. We can recover
${\mathit{x}}$
from
${\mathit{mapB}\;(\mathit{x}\mathbin{:})\;(\mathit{ch}\;\mathrm{0}\;\mathit{xs})}$
if
${\mathit{k}}$
happens to be
${\mathrm{0}}$
because:
That is, the left subtree
${\mathit{up}}$
receives must have the form
${\mathsf{T}\;[ \mathit{x}]}$
, from which we can retrieve
${\mathit{x}}$
and apply
${\mathit{mapB}\;(\mathit{subs}\, {\circ} \,(\mathit{x}\mathbin{:}))}$
to the other subtree. We can furthermore simplify
${\mathit{mapB}\;(\mathit{subs}\, {\circ} \,(\mathit{x}\mathbin{:}))\;(\mathit{ch}\;(\mathrm{1}\mathbin{+}\mathrm{0})\;\mathit{xs})}$
a bit:
The equality above holds because every tip in
${\mathit{ch}\;\mathrm{1}\;\mathit{xs}}$
contains singleton lists and, for a singleton list
${[ \mathit{z}]}$
, we have
${\mathit{subs}\;(\mathit{x}\mathbin{:}[ \mathit{z}])\mathrel{=}[ [ \mathit{x}],[ \mathit{z}]]}$
. In summary, we have established
Case 3.2.
${\mathrm{0}\mathbin{<}\mathit{k}}$
(and
${\mathit{k}\mathbin{<}\mathit{length}\;\mathit{xs}\mathbin{-}\mathrm{1}}$
). In this case, we have to construct (4.2.1), that is,
${\mathit{mapB}\;(\mathit{subs}\, {\circ} \,(\mathit{x}\mathbin{:}))\;(\mathit{ch}\;(\mathrm{1}\mathbin{+}\mathit{k})\;\mathit{xs})}$
, out of the two subtrees,
${\mathit{mapB}\;(\mathit{x}\mathbin{:})\;(\mathit{ch}\;\mathit{k}\;\mathit{xs})}$
and
${\mathit{ch}\;(\mathrm{1}\mathbin{+}\mathit{k})\;\mathit{xs}}$
, without knowing what
${\mathit{x}}$
is.
What follows is perhaps the most tricky part of the derivation. Starting from
${\mathit{mapB}\;(\mathit{subs}\, {\circ} \,(\mathit{x}\mathbin{:}))\;(\mathit{ch}\;(\mathrm{1}\mathbin{+}\mathit{k})\;\mathit{xs})}$
, we expect to use induction somewhere; therefore, a possible strategy is to move
${\mathit{mapB}\;\mathit{subs}}$
rightward, next to
${\mathit{ch}}$
, in order to apply (4.1). Let us consider
${\mathit{mapB}\;(\mathit{subs}\, {\circ} \,(\mathit{x}\mathbin{:}))\;\mathit{u}}$
for a general
${\mathit{u}}$
, and try to move
${\mathit{mapB}\;\mathit{subs}}$
next to
${\mathit{u}}$
.
-
• By definition,
$\mathit{subs}\;(\mathit{x}\mathbin{:}\mathit{xs})\mathrel{=}\mathit{map}\;(\mathit{x}\mathbin{:})\;(\mathit{subs}\;\mathit{xs})\mathbin{+}\mskip-8mu{+}$
[ xs]. That is,
${\mathit{subs}\, {\circ} \,(\mathit{x}\mathbin{:})\mathrel{=}\lambda \mathit{xs}\to \mathit{snoc}\;(\mathit{map}\;(\mathit{x}\mathbin{:})\;(\mathit{subs}\;\mathit{xs}))\;\mathit{xs}}$
—it duplicates the argument
${\mathit{xs}}$
and applies
${\mathit{map}\;(\mathit{x}\mathbin{:})\, {\circ} \,\mathit{subs}}$
to one of them, before calling
${\mathit{snoc}}$
. -
•
${\mathit{mapB}\;(\mathit{subs}\, {\circ} \,(\mathit{x}\mathbin{:}))}$
does the above to each list in the tree
${\mathit{u}}$
. -
• Equivalently, we may also duplicate each values in
${\mathit{u}}$
to pairs, before applying
${\lambda (\mathit{xs},\mathit{xs'})\to \mathit{snoc}\;(\mathit{map}\;(\mathit{x}\mathbin{:})\;(\mathit{subs}\;\mathit{xs}))\;\mathit{xs'}}$
to each pair. -
• Values in
${\mathit{u}}$
can be duplicated by zipping
${\mathit{u}}$
to itself, that is,
${\mathit{zipBW}\;\mathit{pair}\;\mathit{u}\;\mathit{u}}$
where
${\mathit{pair}\;\mathit{xs}\;\mathit{xs'}\mathrel{=}(\mathit{xs},\mathit{xs'})}$
.
With the idea above in mind, we calculate:
We have shown that
which brings
${\mathit{mapB}\;\mathit{subs}}$
next to
${\mathit{u}}$
. The naturality of
${\mathit{zipBW}}$
in the last step is the property that, provided that
${\mathit{h}\;(\mathit{f}\;\mathit{x}\;\mathit{y})\mathrel{=}\mathit{k}\;(\mathit{g}\;\mathit{x})\;(\mathit{r}\;\mathit{y})}$
, we have:
Back to (4.2.1), we may then calculate:
Recall that our aim is to find a suitable definition of
${\mathit{up}}$
such that (4.2) equals (4.3). The calculation shows that we may let
In summary, we have constructed:
which is the mysterious four-line function in Bird (Reference Bird2008)! There is only one slight difference: where we use
${\mathit{snoc}}$
, Bird used
${(\mathbin{:})}$
, which has an advantage of being more efficient. Had we specified
${\mathit{subs}}$
and
${\mathit{choose}}$
differently, we would have derived the
${(\mathbin{:})}$
version, but either the proofs so far would have to proceed in terms of snoc lists, or the sublists in our examples would come in a less intuitive order. For clarity, we chose to present this version. For curious readers, code of the
${(\mathbin{:})}$
version of
${\mathit{up}}$
is given in Appendix A.
An Example.
To demonstrate how
${\mathit{up}}$
works, shown at the bottom of Figure 4 is the tree built by
${\mathit{mapB}\;\mathit{h}\;(\mathit{ch}\;\mathrm{2}\;\mathtt{abcde})}$
. If we apply
${\mathit{up}}$
to this tree, the fourth clause of
${\mathit{up}}$
is matched, and we traverse along its right spine until reaching
${\mathit{t}_{0}}$
, which matches the second clause of
${\mathit{up}}$
, and a singleton tree containing
${[ \mathit{h}\;\mathtt{cd},\mathit{h}\;\mathtt{ce},\mathit{h}\;\mathtt{de}]}$
is generated.
Fig. 4. Applying
$\mathit{mapB}\;\mathit{g}\; \circ \mathit{up}$
to
${\mathit{mapB}\;\mathit{h}\;(\mathit{ch}\;\mathrm{2}\;\mathtt{abcde})}. We abbreviate {\mathit{zipBW}\;\mathit{snoc}}$
to
${\mathit{zip}}$
.
Traversing backward,
${\mathit{up}\;\mathit{t}_{1}}$
generates
${\mathit{u}_{0}}$
, which shall have the same shape as
${\mathit{t}_{0}}$
and can be zipped together to form
${\mathit{u}_{1}}$
. Similarly,
${\mathit{up}\;\mathit{t}_{3}}$
generates
${\mathit{u}_{2}}$
, which shall have the same shape as
${\mathit{t}_{2}}$
. Zipping them together, we get
${\mathit{u}_{3}}$
. They constitute
${\mathit{mapB}\;\mathit{h}\;(\mathit{ch}\;\mathrm{3}\;\mathtt{abcde})}$
, shown at the top of Figure 4.
4.3 Interlude: Shape constraints with dependent types
While the derivation guarantees that the function
${\mathit{up}}$
, as defined above, satisfies (4.1), the partiality of
${\mathit{up}}$
still makes one uneasy. Why is it that
${\mathit{up}\;\mathit{t}}$
in the second clause always returns a
${\mathsf{T}}$
? What guarantees that
${\mathit{up}\;\mathit{t}}$
and
${\mathit{u}}$
in the last clause always have the same shape and can be zipped together? In this section, we try to gain more understanding of the tree construction with the help of dependent types.
Certainly,
${\mathit{ch}}$
does not generate all trees of type
${\mathsf{B}}$
, but only those trees having certain shapes. We can talk about the shapes formally by annotating
${\mathsf{B}}$
with indices, as in the following Agda datatype:
The intention is that
${\mathsf{B}\;\mathit{a}\;\mathit{k}\;\mathit{n}}$
is the tree representing choosing
${\mathit{k}}$
elements from a list of length
${\mathit{n}}$
. Notice that the changes of indices in
${\mathsf{B}}$
follow the definition of
${\mathit{ch}}$
. We now have two base cases,
${\mathsf{T}_{0}}$
and
${\mathsf{T}}_{\mathit{n}}$
, corresponding to choosing
${\mathrm{0}}$
elements and all elements from a list. A tree
${\mathsf{N}\;\mathit{t}\;\mathit{u}\mathbin{:}\mathsf{B}\;\mathit{a}\;(\mathrm{1}\mathbin{+}\mathit{k})\;(\mathrm{1}\mathbin{+}\mathit{n})}$
represents choosing
${\mathrm{1}\mathbin{+}\mathit{k}}$
elements from a list of length
${\mathrm{1}\mathbin{+}\mathit{n}}$
, and the two ways to do so are
${\mathit{t}\mathbin{:}\mathsf{B}\;\mathit{a}\;\mathit{k}\;\mathit{n}}$
(choosing
${\mathit{k}}$
from
${\mathit{n}}$
) and
${\mathit{u}\mathbin{:}\mathsf{B}\;\mathit{a}\;(\mathrm{1}\mathbin{+}\mathit{k})\;\mathit{n}}$
(choosing
${\mathrm{1}\mathbin{+}\mathit{k}}$
from
${\mathit{n}}$
). With the definition,
${\mathit{ch}}$
may have type
where
${\mathsf{Vec}\;\mathit{a}\;\mathit{n}}$
denotes a list (vector) of length
${\mathit{n}}$
.
One can see that a pair of
${(\mathit{k},\mathit{n})}$
uniquely determines the shape of the tree. Furthermore, one can also prove that
${\mathsf{B}\;\mathit{a}\;\mathit{k}\;\mathit{n}\to \mathit{k}\leq \mathit{n}}$
, that is, if a tree
${\mathsf{B}\;\mathit{a}\;\mathit{k}\;\mathit{n}}$
can be built at all, it must be the case that
${\mathit{k}\leq \mathit{n}}$
.
The Agda implementation of
${\mathit{up}}$
has the following type:
The type states that it is defined only for
${\mathrm{0}\mathbin{<}\mathit{k}\mathbin{<}\mathit{n}}$
; the shape of its input tree is determined by
${(\mathit{k},\mathit{n})}$
; the output tree has shape determined by
${(\mathrm{1}\mathbin{+}\mathit{k},\mathit{n})}$
, and the values in the tree are lists of length
${\mathrm{1}\mathbin{+}\mathit{k}}$
. One can also see from the types of its components that, for example, the two trees given to
${\mathit{zipBW}}$
always have the same shape. More details are given in Appendix B.
In Case 2 of Section 4.2, we saw a function
${\mathit{unT}}$
. Its dependently typed version has type
${\mathsf{B}\;\mathit{a}\;(\mathrm{1}\mathbin{+}\mathit{n})\;(\mathrm{1}\mathbin{+}\mathit{n})\to \mathit{a}}$
. It always succeeds because a tree having type
${\mathsf{B}\;\mathit{a}\;(\mathrm{1}\mathbin{+}\mathit{n})\;(\mathrm{1}\mathbin{+}\mathit{n})}$
must be constructed by
$\mathsf{T}_{\mathit{n}}$
—for
${\mathsf{N}\;\mathit{t}\;\mathit{u}}$
to have type
${\mathsf{B}\;\mathit{a}\;(\mathrm{1}\mathbin{+}\mathit{n})\;(\mathrm{1}\mathbin{+}\mathit{n})}$
,
${\mathit{u}}$
would have type
${\mathsf{B}\;\mathit{a}\;(\mathrm{1}\mathbin{+}\mathit{n})\;\mathit{n}}$
, an empty type.
Dependent types help us rest assured that the “partial” functions we use are actually safe. The current notations, however, are designed for interactive theorem proving, not program derivation. The author derives program on paper by equational reasoning in a more concise notation and double-checks the details by theorem prover afterward. All the proofs in this pearl have been translated to Agda. For the rest of the pearl, we switch back to non-dependently typed equational reasoning.
Pascal’s Triangle.
With so much discussion about choosing, it is perhaps not surprising that the sizes of subtrees along the right spine of a
${\mathsf{B}}$
tree correspond to prefixes of diagonals in Pascal’s Triangle. After all, the
${\mathit{k}}$
-th diagonal (counting from zero) in Pascal’s Triangle denotes binomial coefficients—the numbers of ways to choose
${\mathit{k}}$
elements from
${\mathit{k}}$
,
${\mathit{k}\mathbin{+}\mathrm{1}}$
,
${\mathit{k}\mathbin{+}\mathrm{2}}$
… elements. This is probably why Bird (Reference Bird2008) calls the data structure a binomial tree, hence the name
${\mathsf{B}}$
.Footnote
2
See Figure 5 for example. The sizes along the right spine of
${\mathit{ch}\;\mathrm{2}\;\mathtt{abcde}}$
, that is,
${\mathrm{10},\mathrm{6},\mathrm{3},\mathrm{1}}$
, is the second diagonal (in orange), while the right spine of
${\mathit{ch}\;\mathrm{3}\;\mathtt{abcde}}$
is the fourth diagonal (in blue). Applying
${\mathit{up}}$
to a tree moves it rightward and downward. In a sense, a
${\mathsf{B}}$
tree represents a prefix of a diagonal in Pascal’s Triangle with a proof of how it is constructed.
Fig. 5. Sizes of
${\mathsf{B}}$
alone the right spine correspond to prefixes of diagonals in Pascal’s Triangle.
5 The bottom-up algorithm
Now that we have constructed an
${\mathit{up}}$
that satisfies (4.1), it is time to derive the main algorithm. Recall that we have defined, in Section 2,
${\mathit{h}\;\mathit{xs}\mathrel{=}\mathit{td}\;(\mathit{length}\;\mathit{xs}\mathbin{-}\mathrm{1})\;\mathit{xs}}$
, where
The intention is that
${\mathit{td}\;\mathit{n}}$
is a function defined for inputs of length exactly
${\mathrm{1}\mathbin{+}\mathit{n}}$
. We also define a variation:
The difference is that
${\mathit{td'}}$
calls only
${\mathit{ex}}$
in the base case. It takes only a routine induction to show that
${\mathit{td}\;\mathit{n}\mathrel{=}\mathit{td'}\;\mathit{n} \, \, {\circ} \, \, \mathit{map}\;\mathit{f}}$
. All the calls to
${\mathit{f}}$
are thus factored to the beginning of the algorithm. We may then focus on transforming
${\mathit{td'}}$
.
Note that for
${\mathit{ch}\;\mathit{n}\;\mathit{xs}}$
where
${\mathit{n}\mathrel{=}\mathit{length}\;\mathit{xs}}$
always results in
${\mathsf{T}\;\mathit{xs}}$
. That is, we have
Our main theorem is that
Theorem 1. For all
${\mathit{n}\mathbin{::}\mathbb{N}}$
we have
${\mathit{td}\;\mathit{n}\mathrel{=}\mathit{bu}\;\mathit{n}}$
, where
That is, the top-down algorithm
${\mathit{td}\;\mathit{n}}$
is equivalent to a bottom-up algorithm
${\mathit{bu}\;\mathit{n}}$
, where the input is preprocessed by
${\mathit{mapB}\;\mathit{ex}\, {\circ} \,\mathit{ch}\;\mathrm{1}\, {\circ} \,\mathit{map}\;\mathit{f}}$
, followed by
${\mathit{n}}$
steps of
${\mathit{mapB}\;\mathit{g}\, {\circ} \,\mathit{up}}$
. By then we will have a singleton tree, whose content can be extracted by
${\mathit{unT}}$
.
Proof. Let
${\mathit{length}\;\mathit{xs}\mathrel{=}\mathrm{1}\mathbin{+}\mathit{n}}$
. We reason:
The real work is done in Lemma 1 below. It shows that
${\mathit{mapB}\;(\mathit{td'}\;\mathit{n})\, {\circ} \,\mathit{ch}\;(\mathrm{1}\mathbin{+}\mathit{n})}$
can be performed by processing the input by
${\mathit{mapB}\;\mathit{ex}\, {\circ} \,\mathit{ch}\;\mathrm{1}}$
, before
${\mathit{n}}$
steps of
${\mathit{mapB}\;\mathit{g}\, {\circ} \,\mathit{up}}$
. This is the key lemma that relates (4.1) to the main algorithm.
Lemma 1. For inputs of length
${\mathrm{1}\mathbin{+}\mathit{n}}$
(
${\mathit{n}\mathbin{>}\mathrm{1}}$
), we have
Proof. For
${\mathit{n}\mathbin{:=}\mathrm{0}}$
both sides simplify to
${\mathit{mapB}\;\mathit{ex}\, {\circ} \,\mathit{ch}\;\mathrm{1}}$
. For
${\mathit{n}\mathbin{:=}\mathrm{1}\mathbin{+}\mathit{n}}$
, we start from the LHS, assuming an input of length
${\mathrm{2}\mathbin{+}\mathit{n}}$
:
6 Conclusion and discussions
We have derived the mysterious four-line function of Bird (Reference Bird2008) and built upon it a bottom-up algorithm that solves the sublists problem. The specifications (3.1) and (4.1) may look trivial in retrospect, but it did took the author a lot of efforts to discover them. In typical program calculation, one starts with a specification of the form
${\mathit{up}\;\mathit{t}\mathrel{=}\mathit{rhs}}$
, where
${\mathit{t}}$
, the argument to the function to be derived, is a variable. One then tries to pattern match on
${\mathit{t}}$
, simplifies
${\mathit{rhs}}$
, and finds an inductive definition of
${\mathit{up}}$
. The author has tried to find such a specification with no avail, before settling down on (3.1) and (4.1), where
${\mathit{up}}$
is applied to a function call. Once (4.1) is found, the rest of the development is tricky at times, but possible. The real difficulty is that when we get stuck in the calculation, we may hardly know which is the major source of the failure—the insufficiency of the specification, or the lack of a clever trick to bridge the gap. Techniques for performing such calculations to find a solution for
${\mathit{up}}$
is one of the lessons the author learned from this experience.
Some final notes on the previous works. The sublists problem was one of the examples of Bird & Hinze (Reference Bird and Hinze2003), a study of memoization of functions, with a twist: the memo table is structured according to the call graph of the function, using trees of shared nodes (which they called nexuses). To solve the sublists problem, Bird & Hinze (Reference Bird and Hinze2003) introduced a data structure, also called a “binomial tree”. Whereas the binomial tree in Bird (Reference Bird2008) and in this pearl models the structure of the function
${\mathit{choose}}$
, that in Bird & Hinze (Reference Bird and Hinze2003) can be said to model the function computing all sublists:
Such trees were then extended with up links (and became nexuses). Trees were built in a top-down manner, creating carefully maintained links going up and down.
Bird then went on to study the relationship between top-down and bottom-up algorithms, and the sublists problem was one of the examples in Bird (Reference Bird2008) to be solved bottom-up. In Bird’s formulation, the function used in the top-down algorithm that decomposes problems into sub-problems (like our
${\mathit{subs}}$
) is called
${\mathit{dc}}$
, with type
${\mathsf{L}\;\mathit{a}\to \mathsf{F}\;(\mathsf{L}\;\mathit{a})}$
for some functor
${\mathsf{F}}$
. The bottom-up algorithm uses a function
${\mathit{cd}}$
(like our
${\mathit{upgrade}}$
), with type
${\mathsf{L}\;\mathit{a}\to \mathsf{L}\;(\mathsf{F}\;\mathit{a})}$
. One of the properties they should satisfy is
${\mathit{dc}\, {\circ} \,\mathit{cd}\mathrel{=}\mathit{mapF}\;\mathit{cd}\, {\circ} \,\mathit{dc}}$
, where
${\mathit{mapF}}$
is the functorial mapping for
${\mathsf{F}}$
.
For the sublists problem,
${\mathit{dc}\mathrel{=}\mathit{subs}}$
, and
${\mathsf{F}\mathrel{=}\mathsf{L}}$
. We know parts of the rest of the story: Bird had to introduce a new datatype
${\mathsf{B}}$
, and a new
${\mathit{cd}}$
with type
${\mathsf{B}\;\mathit{a}\to \mathsf{B}\;(\mathsf{L}\;\mathit{a})}$
, the four-line function that inspired this pearl. That was not all, however. Bird also quickly introduced, on the last page of the paper, a new
${\mathit{dc'}\mathbin{::}\mathsf{B}\;\mathit{a}\to \mathsf{L}\;(\mathsf{B}\;\mathit{a})}$
, which was as cryptic as
${\mathit{cd}}$
, and claimed that
${\mathit{dc'}\, {\circ} \,\mathit{cd}\mathrel{=}\mathit{mapF}\;\mathit{cd}\, {\circ} \,\mathit{dc'}}$
. The relationship between
${\mathit{dc'}}$
and
${\mathit{dc}}$
(and the original problem) was not clear. In this pearl, we took a shorter route, proving directly that the bottom-up algorithm works, and the step function is
${\mathit{mapB}\;\mathit{g}\, {\circ} \,\mathit{up}}$
.
Acknowledgments
The author would like to thank Hsiang-Shang Ko and Jeremy Gibbons for many in-depth discussions throughout the development of this work, Conor McBride for discussion at a WG 2.1 meeting, and Yu-Hsuan Wu and Chung-Yu Cheng for proof-reading drafts of this pearl. The examples of how the immediate sublists problem may be put to work was suggested by Meng-Tsung Tsai. The first version of the Agda proofs was constructed by You-Zheng Yu.
Conflicts of interest
None.
Supplementary material
For supplementary material for this article, please visit https://doi.org/10.1017/S0956796824000145.
A Variation of
${\mathit{up}}$
That Uses
${(\mathbin{:})}$
Show below is the variation of
${\mathit{up}}$
that uses
${(\mathbin{:})}$
. The function is called
${\mathit{cd}}$
in Bird (Reference Bird2008).
B Agda Implementation of
${\mathit{up}}$
The following is an Agda implementation of
${\mathit{up}}$
. The type states that it is defined only for
${\mathrm{0}\mathbin{<}\mathit{k}\mathbin{<}\mathit{n}}$
; the shape of its input tree is determined by
${(\mathit{k},\mathit{n})}$
; the output tree has shape determined by
${(\mathrm{1}\mathbin{+}\mathit{k},\mathit{n})}$
, and the values in the tree are lists of length
${\mathrm{1}\mathbin{+}\mathit{k}}$
.
The first three clauses of
${\mathit{up}}$
eliminate impossible cases. The remaining four clauses are essentially the same as in the non-dependently typed version, modulo the additional arguments and proof terms, shown in light brown, that are needed to prove that
${\mathit{k}}$
and
${\mathit{n}}$
are within bounds. In the clause that uses
${\mathit{unT}}$
, the input tree has the form
$\mathsf{N}\;\mathit{t}\;(\mathsf{T}_{\mathit{n}}$
q). The right subtree being a
$\mathsf{T}_{\mathit{n}}$
forces the other subtree
${\mathit{t}}$
to have type
${\mathsf{B}\;\mathit{a}\;(\mathrm{1}\mathbin{+}\mathit{k})\;(\mathrm{2}\mathbin{+}\mathit{k})}$
—the two indices must differ by
${\mathrm{1}}$
. Therefore,
${\mathit{up}\;\mathit{t}}$
has type
${\mathsf{B}\;\mathit{a}\;(\mathrm{2}\mathbin{+}\mathit{k})\;(\mathrm{2}\mathbin{+}\mathit{k})}$
and must be built by
$\mathsf{T}_{\mathit{n}}$
. The last clause receives inputs having type
${\mathsf{B}\;\mathit{a}\;(\mathrm{2}\mathbin{+}\mathit{k})\;(\mathrm{2}\mathbin{+}\mathit{n})}$
. Both
${\mathit{u}}$
and
${\mathit{up}\;\mathit{t}}$
have types
${\mathsf{B}\mathbin{...}(\mathrm{2}\mathbin{+}\mathit{k})\;(\mathrm{1}\mathbin{+}\mathit{n})}$
and, therefore, have the same shape.
Open access
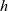
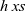
Discussions
No Discussions have been published for this article.