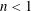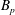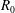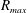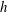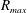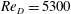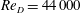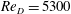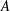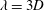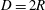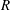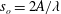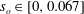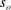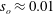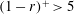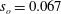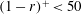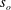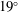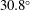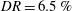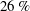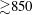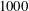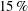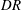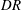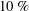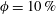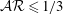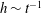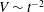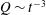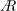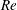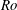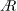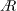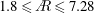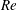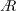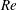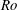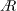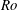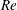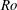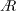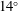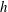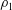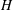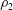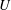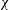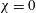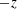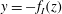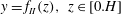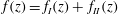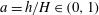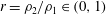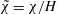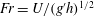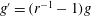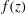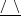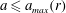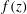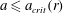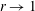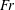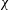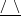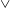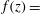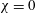Single-flagellated bacteria propel themselves by rotating a flagellar motor, translating rotation to the filament through a compliant hook and subsequently driving the rotation of the flagellum. The flagellar motor alternates the direction of rotation between counterclockwise and clockwise, and this leads to the forward and backward directed swimming. Such bacteria can change the course of swimming as the hook experiences its buckling caused by the change of bending rigidity. In this paper, we present a comprehensive model of a monotrichous bacterium as a free swimmer in a viscous fluid. We describe a cell body as a rigid body using the penalty method and a flagellum as an elastic rod using Kirchhoff rod theory. The hydrodynamic interaction of the bacterium is described by the regularized Stokes formulation. Our model of a single-flagellated micro-organism is able to mimic a swimming pattern that is well matched with the experimental observation. Furthermore, we find the critical thresholds of the rotational frequency of the motor and the bending modulus of the hook for the buckling instability, and investigate the dependence of the buckling angle and the reorientation of the swimming cell after buckling on the physical and geometrical parameters of the model.

We investigate the deformation of a linear viscoelastic compliant coating in a turbulent flow for a wide range of coating parameters. A one-way coupling model is proposed in which the turbulent surface stresses are expressed as a sum of streamwise-travelling waves with amplitudes determined from the stress spectra of the corresponding flow over a rigid wall. The analytically calculated coating deformation is analysed in terms of the root-mean-square (r.m.s.) surface displacement and the corresponding point frequency spectra. The present study systematically investigates the influence of five coating properties namely density, stiffness, thickness, viscoelasticity and compressibility. The surface displacements increase linearly with the fluid/solid density ratio. They are linearly proportional to the coating thickness for thin coatings, while they become independent of the thickness for thick coatings. Very soft coatings show resonant behaviour, but the displacement for stiffer coatings is proportional to the inverse of the shear modulus. The viscoelastic loss angle has only a significant influence when resonances occur in the coating response, while Poisson’s ratio has a minor effect for most cases. The modelled surface displacement is qualitatively compared with recent measurements on the deformation of three different coatings in a turbulent boundary-layer flow. The model predicts the order of magnitude of the surface displacement, and it captures the increase of the coating displacement with the Reynolds number and the coating softness. Finally, we propose a scaling that collapses all the experimental data for the r.m.s. of the vertical surface displacement onto a single curve.

Researches on nonlinear instability of power-law plane sheets have been conducted using the Carreau model as the constitutive model. Combined with asymptotic expansion and long-wave assumption, the governing equations and boundary conditions were manipulated using integral transform. The first-order dimensionless dispersion relation between unstable growth rate and wavenumber was obtained and the second-order interface disturbance amplitude was calculated. By comparison and analysis of components of the second-order interface disturbance amplitude, it was found that the power-law index $n$ ($n<1$) only had an impact on instability of waves with the fundamental wavelength or one third the fundamental wavelength. The findings show that the Carreau-law rheological parameter $B_{p}$ has little impact on the second-order disturbance amplitude at the interfaces in a practical situation, while the Reynolds number has a positive effect on the growth rate of the disturbance amplitude for the power-law liquid sheets. Finally, the growth rates obtained by numerical simulation and analytical solution have been compared, and the results showed good agreement in the initial phase of wave evolution.

An explosive gas mixture of hydrogen and oxygen is introduced in liquid water between two horizontal walls, forming a flat cylindrical bubble. Ignition and explosion of the bubble lead to a large depressurized cavity that finally implodes. We investigate the dynamics of the bubble collapse, which is qualitatively similar to the collapse of a spherical bubble. It exhibits a slightly weaker singularity than for spherical bubbles. We also analyse the explosion process. Starting with an initial radius $R_{0}$, the bubble reaches a maximal radius $R_{max}$ that depends on the gap thickness $h$ between the two walls: for a thinner gap, the condensation of water vapour is more efficient, the overpressure consecutive to the combustion is weaker, and its duration is shorter. This leads to a smaller maximal radius $R_{max}$. An indirect measurement of the transport coefficient of hot water vapour can be inferred from this observation.

We present a new approach – the entropy-viscosity method (EVM) – for numerical modelling of high Reynolds number flows and investigate its potential by simulating fully developed incompressible turbulent flow, first in a stationary pipe and subsequently in a flexible pipe. This method, which was first proposed by Guermond et al. (J. Comput. Phys., vol. 230 (11), 2011, pp. 4248–4267), introduces the concept of entropy viscosity, computed based on the nonlinear localized residual obtained from the energy equation. Specifically, this nonlinear viscosity based on the local size of entropy production is added to the spectral element discretization employed in our work for stabilization at insufficient resolution. Unlike its original formulation, which includes an ad hoc tuneable parameter $\unicode[STIX]{x1D6FC}$, here, we determine the value of $\unicode[STIX]{x1D6FC}$ by assuming that the entropy viscosity is analogous to the eddy viscosity of the Smagorinsky model. However, the overall approach has the flavour of the implicit large eddy simulation (ILES) instead of the standard large eddy simulation (LES). Given the empiricism of our approach, we have performed systematic studies of homogeneous isotropic turbulence for validation (see appendix A). We have also carried out a more complete numerical simulation study to investigate incompressible turbulent flow in a stationary pipe at 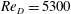$Re_{D}=5300$ and 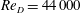$Re_{D}=44\,000$, following the work of Wu & Moin (J. Fluid Mech., vol. 608, 2008, pp. 81–112) who performed very accurate direct numerical simulations (DNS) of these two cases. We found that the mean flow, turbulence fluctuations, and two-point correlations of the EVM-based LES are in good agreement with the DNS of Wu & Moin despite the fact that we employed grids with resolution two orders of magnitude smaller. If we instead use the standard Smagorinsky model in our simulations, the computations become unstable due to insufficient resolution of the smaller scales. Another important difference is that the entropy-viscosity model scales with the cube of the distance from the wall and approaches zero at the wall, which is theoretically correct, as shown by our a posteriori tests. Based on the validated EVM approach, we then simulated fully developed turbulent flow at 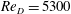$Re_{D}=5300$ in a flexible pipe subject to prescribed vibrations in the cross-flow plane corresponding to a standing wave of amplitude 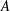$A$ and wavelength 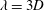$\unicode[STIX]{x1D706}=3D$, where 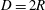$D=2R$ is the pipe diameter and 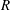$R$ is the radius. We have simulated 11 cases corresponding to increasing values of wave steepness 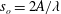$s_{o}=2A/\unicode[STIX]{x1D706}$, with 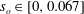$s_{o}\in [0,0.067]$. We found a quadratic dependence of the friction factor on 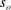$s_{o}$ with the minimum at approximately 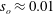$s_{o}\approx 0.01$, so, surprisingly, we have a slight decrease in drag at first and then a substantial increase compared to the stationary pipe. To obtain the turbulence statistics, we averaged the simulated flow over twenty time periods at the nodes and anti-nodes separately. We found substantial changes in the mean velocity profile at distances 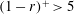$(1-r)^{+}>5$ while the peaks of turbulent intensities were amplified by 50 % in the axial direction and by 200 % in the normal and azimuthal directions at 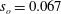$s_{o}=0.067$. The peak shear stress at the node increased by more than 200 % whereas at the anti-node it attained negative values. Turbulent budgets revealed large changes close to the wall at 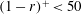$(1-r)^{+}<50$ while flow visualizations showed that many more strong worm-like vortices were generated in the near-wall regions compared to the stationary pipe. We have also computed various spatio-temporal correlations that show that the pressure fluctuations are very sensitive to the pipe vibration and scale quadratically with 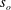$s_{o}$. Both pressure and velocity correlations exhibit cellular patterns consistent with the standing-wave pipe motion.

Direct numerical simulation of incompressible turbulence in a straight square duct finds the post-transition flow evolving substantially, and for Reynolds numbers based on the friction velocity and duct hydraulic radius greater than 600 a two-structure secondary flow regime has been established, suggesting the coexistence of two distinct sources of mean streamwise vorticity. The nominal source terms in the equation for the mean streamwise vorticity involve turbulent variables only, that allow us to identify the dominant dynamical process that marks and/or sustains the transverse mean flow. Close to the corner a mean profile instability is dominant, while farther away turbulent streamwise vorticity intensification is broadly distributed near the duct walls. The instability-driven secondary velocity maximum on the duct diagonals scales with the friction velocity. There is limited scaling of turbulent intensities on the wall bisectors.

A direct numerical simulation of the three-dimensional unsteady compressible Navier–Stokes equations is performed to investigate the infrasonic field generated in a realistic atmosphere by an explosive source placed at ground level. To this end, a high-order finite-difference method originally developed for aeroacoustic applications is employed. The maximum overpressure and the main frequency of the signal recorded at 4 km distance from the source location are about 4000 Pa and 0.2 Hz, respectively. The atmosphere is parametrized as a vertically stratified medium, constructed by specifying vertical profiles of the temperature and the horizontal wind which reproduce measurements. The computation is carried out up to 140 km altitude and 450 km range. The goal of the present paper is twofold. On the one hand, the feasibility of using a direct numerical simulation of the three-dimensional fluid dynamic equations for the detailed description of long-range propagation in the atmosphere is proven. On the other hand, a physical analysis of the infrasonic field is realized. In particular, great attention is directed towards some important phenomena which are not taken into account or not well predicted by classical propagation models. To begin with, the present study clearly demonstrates that the weakly nonlinear ray theory may lead to an incorrect evaluation of the waveform distortion of high-amplitude waves propagating towards the lower thermosphere. In addition, signals recorded in the shadow zones are investigated. In this regard, the influence on the acoustic field of temperature and wind inhomogeneities of length scale comparable with the acoustic wavelength is analysed. The role of diffraction at the thermospheric caustic is finally examined and it is pointed out that the amplitude of the source may have a strong impact on the length of the shadow zone.

In this paper we highlight that extreme events such as freak waves are a transient phenomenon in keeping with the old fisherman tale that these extreme events seem to appear out of nowhere. Janssen (J. Phys. Oceanogr., vol. 33, 2003, pp. 863–884) obtained an evolution equation for the ensemble average of the excess kurtosis, which is a measure for the deviation from normality and an indicator for nonlinear focusing resulting in extreme events. In the limit of a narrow-band wave train, whose dynamics is governed by the two-dimensional nonlinear Schrödinger (NLS) equation, the excess kurtosis is under certain conditions seen to grow to a maximum after which it decays to zero for large times. This follows from a numerical solution of the problem and also from an analytical solution presented by Fedele (J. Fluid Mech., vol. 782, 2015, pp. 25–36). The analytical solution is not explicit because it involves an integral from initial time to actual time. We therefore study a number of properties of the integral expression in order to better understand some interesting features of the time-dependent excess kurtosis and the generation of extreme events.

The local flow topology analysis of the primary atomization of liquid jets has been conducted using the invariants of the velocity-gradient tensor. All possible small-scale flow structures are categorized into two focal and two nodal topologies for incompressible flows in both liquid and gaseous phases. The underlying direct numerical simulation database was generated by the one-fluid formulation of the two-phase flow governing equations including a high-fidelity volume-of-fluid method for accurate interface propagation. The ratio of liquid-to-gas fluid properties corresponds to a diesel jet exhausting into air. Variation of the inflow-based Reynolds number as well as Weber number showed that both these non-dimensional numbers play a pivotal role in determining the nature of the jet break-up, but the flow topology behaviour appears to be dominated by the Reynolds number. Furthermore, the flow dynamics in the gaseous phase is generally less homogeneous than in the liquid phase because some flow regions resemble a laminar-to-turbulent transition state rather than fully developed turbulence. Two theoretical models are proposed to estimate the topology volume fractions and to describe the size distribution of the flow structures, respectively. In the latter case, a simple power law seems to be a reasonable approximation of the measured topology spectrum. According to that observation, only the integral turbulent length scale would be required as an input for the a priori prediction of the topology size spectrum.

The effect of an electric field on the coalescence of two water drops suspended in an insulating oil is investigated. We report four new results. (i) The cone angle for the non-coalescence of drops can be significantly smaller (as small as $19^{\circ }$) than the value of $30.8^{\circ }$ reported by Bird et al. (Phys. Rev. Lett., vol. 103 (16), 2009, 164502). (ii) A surprising observation of the dependence of the mode of coalescence/non-coalescence on the type of insulating oil is seen. A cone–cone mode for silicone oil is observed as against cone–dimple mode for castor oil. (iii) The critical capillary number for non-coalescence decreases with increase in the conductivity of the droplet phase. (iv) Systematic experiments prove that the apparent bridge during non-coalescence is indeed transitory and not permanent, as reported elsewhere. Theoretical calculations using analytical theory and the boundary integral method explain the formation of the cone–dimple mode as well as the transitory bridge length. The numerical calculation and thereby the physical mechanism to explain the occurrence of very small non-coalescence angles as well as the dependence of the phenomenon on the conductivity of the insulating oil and the water droplets remain unexplained.

Streamwise velocity profiles and their wall-normal derivatives were used to investigate the properties of turbulent channel flow in the low polymer drag reduction $(DR)$ regime ($DR=6.5\,\%$ to $26\,\%$), as realized via polymer injection at the channel surface. Streamwise velocity data were obtained over a friction Reynolds number ranging from $650$ to $1800$ using the single-velocity-component version of molecular tagging velocimetry (1c-MTV). This adaptation of the MTV technique has the ability to accurately capture instantaneous profiles at very high spatial resolution (${\gtrsim}850$ data points per wall-normal profile), and thus generate well-resolved derivative information as well. Owing to this ability, the present study is able to build upon and extend the recent numerical simulation analysis of White et al. (J. Fluid Mech., vol. 834, 2018, pp. 409–433) that examined the mean dynamical structure of polymer drag-reduced channel flow at friction Reynolds numbers up to $1000$. Consistently, the present mean velocity profiles indicate that the extent of the logarithmic region diminishes with increasing polymer concentration, while statistically significant increases in the logarithmic profile slope begin to occur for drag reductions less than $15\,\%$. Profiles of the r.m.s. streamwise velocity indicate that the maximum moves farther from the wall and increases in magnitude with reductions in drag. Similarly, with increasing drag reduction, the profile of the combined Reynolds and polymer shear stress exhibits a decrease in its maximum value that also moves farther from the wall. Correlations are presented that estimate the location and value of the maximum r.m.s. streamwise velocity and combined Reynolds and polymer shear stress. Over the range of $DR$ investigated, these effects consistently exhibit approximately linear trends as a function of $DR$. The present measurements allow reconstruction of the mean momentum balance (MMB) for channel flow, which provides further insights regarding the physics described in the study by White et al. In particular, the present findings support a physical scenario in which the self-similar properties on the inertial domain identified from the leading-order structure of the MMB begin to detectably and continuously vary for drag reductions less than $10\,\%$.

Finite-size particles modulate wall-bounded turbulence, leading, for the case of spherical particles, to increased drag also owing to the formation of a particle wall layer. Here, we study the effect of particle shape on the turbulence in suspensions of spheroidal particles at volume fraction $\unicode[STIX]{x1D719}=10\,\%$ and show how the near-wall particle dynamics deeply changes with the particle aspect ratio and how this affects the global suspension behaviour. Direct numerical simulations are performed using a direct-forcing immersed boundary method to account for the dispersed phase, combined with a soft-sphere collision model and lubrication corrections for short-range particle–particle and particle–wall interactions. The turbulence reduces with the aspect ratio of oblate particles, leading to drag reduction with respect to the single-phase flow for particles with aspect ratio ${\mathcal{A}}{\mathcal{R}}\leqslant 1/3$, when the significant reduction in Reynolds shear stress is more than the compensation by the additional stresses, induced by the solid phase. Oblate particles are found to avoid the region close to the wall, travelling parallel to it with small angular velocities, while preferentially sampling high-speed fluid in the wall region. Prolate particles also tend to orient parallel to the wall and avoid its vicinity. Their reluctance to rotate around the spanwise axis reduces the wall-normal velocity fluctuation of the flow and therefore the turbulence Reynolds stress, similar to oblates; however, they undergo rotations in wall-parallel planes which increase the additional solid stresses due to their relatively larger angular velocities compared to the oblates. These larger additional stresses compensate for the reduction in turbulence activity and lead to a wall drag similar to that of single-phase flows. Spheres on the other hand, form a layer close to the wall with large angular velocities in the spanwise direction, which increases the turbulence activity in addition to exerting the largest solid stresses on the suspension, in comparison to the other studied shapes. Spherical particles therefore increase the wall drag with respect to the single-phase flow.

A new lubrication model solution is found for the late-stage draining of a wetting capillary liquid from a linear interior corner. The solution exploits the symmetry of volumetric sink conditions at opposing ends of such a ‘double-drained’ interior corner flow with applications ranging from liquid recovery in microfluidic devices on Earth to liquid fuel scavenging in large fuel tanks aboard spacecraft. At long times $t$, the nominal liquid depth is $h\sim t^{-1}$, the liquid volume is $V\sim t^{-2}$ and the maximum volumetric liquid removal rate is $Q\sim t^{-3}$. The constraints under which the solution is valid are provided. To qualitatively assess the value of the solution, representative experiments are conducted at larger length scales aboard the International Space Station and at microfluidic length scales in a terrestrial laboratory. Both sets of experiments confirm the predicted power-law dependences. We show that the separation of variables solution offers a method to predict maximum drain rates from related geometries where a single drain location provides the required symmetry of the problem.

The individual and combined influences of aspect ratio ($A$), Reynolds number ($Re$) and Rossby number ($Ro$) on the leading-edge vortex (LEV) of a rotating wing of insect-like planform are investigated numerically. A previous study from our group has determined the wingspan to be an appropriate length scale governing the large-scale LEV structure. In this study, the $A$ range considered is further extended, to show that this scaling works well as $A$ is varied by a factor of 4 ($1.8\leqslant A\leqslant 7.28$) and over a $Re$ range of two orders of magnitude. The present study also extends this scaling for wings with an offset from the rotation axis, which is typically the case for actual insects and often for experiments. Remarkably, the optimum range of $A$ based on the lift coefficients at different $Re$ coincides with that observed in nature. The scaling based on the wingspan is extended to the acceleration terms of the Navier–Stokes equations, suggesting a modified scaling of $Ro$, which decouples the effects of $A$. A detailed investigation of the flow structures, by increasing $Ro$ in a wide range, reveals the weakening of the LEV due to the reduced spanwise flow, resulting in a reduced lift. Overall, the use of span-based scaling of $Re$ and $Ro$, together with $A$, may help reconcile apparent conflicting trends between observed variations in aerodynamic performance in different sets of experiments and simulations.

Atmospheric particulates may be a major source of boundary-layer instabilities leading to laminar–turbulent transition on aerodynamically smooth bodies flying at supersonic speeds. Particulates penetrating into the boundary-layer flow can excite wavepackets of the first- and/or second-mode instability. The packets grow downstream, reach the threshold amplitude and ultimately break down to turbulent spots. A numerical model is developed to simulate excitation of unstable wavepackets by spherical solid particulates. As an example, computations are carried out for a $14^{\circ }$ half-angle sharp wedge flying at an altitude of 20 km, Mach number 4 and zero angle of attack. The numerical results agree satisfactorily with the theory developed by Fedorov (J. Fluid Mech., vol. 737, 2013, pp. 105–131). The numerical model opens up an opportunity to investigate receptivity to particulates for practical supersonic and hypersonic configurations such as blunt bodies of revolution.

We present the solution of the idealized steady-state gravity current of height $h$ and density $\unicode[STIX]{x1D70C}_{1}$ that propagates into an ambient motionless fluid of height $H$ and density $\unicode[STIX]{x1D70C}_{2}$ in a channel of general non-rectangular cross-section, with an upper surface open to the atmosphere, at high Reynolds number. The current propagates with speed $U$ and causes a depth decrease $\unicode[STIX]{x1D712}$ of the top surface. This is a significant extension of Benjamin’s (J. Fluid Mech., vol. 31, 1968, pp. 209–248) seminal solution for the gravity current in a rectangular (or laterally unbounded) channel with a fixed top ($\unicode[STIX]{x1D712}=0$). The determination of $\unicode[STIX]{x1D712}$ is a part of the problem. Supposing that the direction of propagation is $x$ and gravity acceleration $g$ acts in the $-z$ direction, the sidewalls are specified by $y=-f_{I}(z)$ and $y=f_{II}(z),~z\in [0.H]$, and the width is $f(z)=f_{I}(z)+\,f_{II}(z)$. The dimensionless parameters of the problem are $a=h/H\in (0,1)$ and $r=\unicode[STIX]{x1D70C}_{2}/\unicode[STIX]{x1D70C}_{1}\in (0,1)$. We show that a control-volume analysis of the type used by Benjamin produces a system of algebraic equations for $\tilde{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D712}/H$ and $Fr=U/(g^{\prime }h)^{1/2}$ as functions of $a$ and $r$, where $g^{\prime }=(r^{-1}-1)g$ is the reduced gravity. The geometry enters the equation via the width function $f(z)$. We present solutions for typical $f(z)$: rectangle, semi-circle, $\vee$ triangle and trapezoid $\text{}\underline{/~\backslash }$ . The results are physically acceptable and insightful. The non-negative dissipation condition defines the domain of validity $a\leqslant a_{max}(r)$ (also depending on $f(z)$); the equality sign corresponds to energy-conserving cases. The critical speed limitation (with respect to the characteristics) is also considered briefly and suggests a slightly smaller $a\leqslant a_{crit}(r)$. The open-top results in the Boussinesq limit $r\rightarrow 1$ coincide with the fixed-top solution. Upon the reduction of $r$, for a fixed thickness $a$, the value of $Fr$ decreases and $\unicode[STIX]{x1D712}$ increases, until the point of energy-conserving (non-dissipative) flow; for smaller $r$, a negative non-physical dissipation appears. The trends are more pronounced for a converging cross-section geometry (like $\text{}\underline{/~\backslash }$ ) than for the opposite shape (like $\vee$ triangle). The previously investigated Benjamin-type steady-state $Fr$ and dissipation results are particular cases of the new formulation: $f(z)=$ const. reproduces the two-dimensional results, and $\unicode[STIX]{x1D712}=0$ recovers the fixed-top solution.

Two-dimensional steady thermocapillary flows in a liquid layer over a substrate, which has a uniform temperature and sinusoidal topography, are investigated by asymptotic theory. Here, the buoyancy effect is negligible and the interface is not significantly disturbed under low Marangoni number and low capillary number. A temperature gradient along the gas/liquid interface causes recirculating flows. For a small aspect ratio, which yields a sinusoidal topography with a long wavelength relative to the mean depth of the liquid layer, the second-order solutions are obtained analytically. The basic solutions show vertical diffusion of heat and vorticity from the substrate and interface, respectively. In the second corrections, the horizontal diffusion of heat weakens the overall flow and the convection of heat intensifies it.

Two temporally developing isothermal round jets at a Mach number of 0.9 and Reynolds numbers of 3125 and 12 500 are simulated in order to investigate noise generation in high-subsonic jet flows. Snapshots and statistical properties of the flow and sound fields, including mean, root-mean-square and skewness values, spectra and auto- and cross-correlations of velocity and pressure, are presented. The jet at a Reynolds number of 12 500 develops more rapidly, exhibits more fine turbulent scales and generates more high-frequency acoustic waves than the other. In both cases, however, when the jet potential core closes, mixing-layer turbulent structures intermittently intrude on the jet axis and strong low-frequency acoustic waves are emitted in the downstream direction. These waves are dominated by the axisymmetric mode and are significantly correlated with centreline flow fluctuations. These results are similar to those obtained at the end of the potential core of spatially developing jets. They suggest that the mechanism responsible for the downstream noise component of these jets also occurs in temporal jets, regardless of the Reynolds number. This mechanism is revealed by averaging the flow and pressure fields of the present jets using a sample synchronization with the minimum values of centreline velocity at potential-core closing. A spot characterized by a lower velocity and a higher level of vorticity relative to the background flow field is found to develop in the interfacial region between the mixing layer and the potential core, to strengthen rapidly and reach a peak intensity when arriving on the jet axis, and then to break down. This is accompanied by the growth and decay of a hydrodynamic pressure wave, propagating at a velocity which, initially, is close to 65 per cent of the jet velocity and slightly increases, but quickly decreases after the collapse of the high-vorticity spot in the flow. During that process, sound waves are radiated in the downstream direction.

We have performed direct numerical simulation of the turbulent flow of a polymer solution in a square duct, with the FENE-P model used to simulate the presence of polymers. First, a simulation at a fixed moderate Reynolds number is performed and its results compared with those of a Newtonian fluid to understand the mechanism of drag reduction and how the secondary motion, typical of the turbulent flow in non-axisymmetric ducts, is affected by polymer additives. Our study shows that the Prandtl’s secondary flow is modified by the polymers: the circulation of the streamwise main vortices increases and the location of the maximum vorticity moves towards the centre of the duct. In-plane fluctuations are reduced while the streamwise ones are enhanced in the centre of the duct and dumped in the corners due to a substantial modification of the quasi-streamwise vortices and the associated near-wall low- and high-speed streaks; these grow in size and depart from the walls, their streamwise coherence increasing. Finally, we investigated the effect of the parameters defining the viscoelastic behaviour of the flow and found that the Weissenberg number strongly influences the flow, with the cross-stream vortical structures growing in size and the in-plane velocity fluctuations reducing for increasing flow elasticity.

The present work investigates local flow structures and the downstream evolution of the core of helical tip vortices generated by a three-bladed rotor. Earlier experimental studies have shown that the core of a helical tip vortex exhibits a local helical symmetry with a simple relation between the axial and azimuthal velocities. In the present study, a self-similarity scaling argument further describes the downstream development of the vortex core. Self-similarity has up to now only been investigated for longitudinal vortices and it is the first time that helical vortices have become the subject of such an analysis. Combining symmetry arguments from previous studies on helical vortices with novel experiments and knowledge regarding the self-similarity evolution of the core of longitudinal vortices, a new model describing what is referred to as ‘helical self-similarity’ is proposed. The generality of the model is verified and supported by experimental data. The proposed model is important for fundamental understanding of the behaviour of helical vortices, with a range of applications in both industry and nature. Examples of this are tip vortices behind aerodynamic devices, such as vortex generators, and fixed and rotary aircraft, and in combustion chambers and cyclone separators.