Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T22:47:56.294Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence modulation in channel flow of finite-size spheroidal particles

Published online by Cambridge University Press:  26 November 2018

M. Niazi Ardekani Open the ORCID record for M. Niazi Ardekani [Opens in a new window]  and
L. Brandt Open the ORCID record for L. Brandt [Opens in a new window]
M. Niazi Ardekani*
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
L. Brandt
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Finite-size particles modulate wall-bounded turbulence, leading, for the case of spherical particles, to increased drag also owing to the formation of a particle wall layer. Here, we study the effect of particle shape on the turbulence in suspensions of spheroidal particles at volume fraction 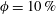$\unicode[STIX]{x1D719}=10\,\%$ and show how the near-wall particle dynamics deeply changes with the particle aspect ratio and how this affects the global suspension behaviour. Direct numerical simulations are performed using a direct-forcing immersed boundary method to account for the dispersed phase, combined with a soft-sphere collision model and lubrication corrections for short-range particle–particle and particle–wall interactions. The turbulence reduces with the aspect ratio of oblate particles, leading to drag reduction with respect to the single-phase flow for particles with aspect ratio 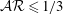${\mathcal{A}}{\mathcal{R}}\leqslant 1/3$, when the significant reduction in Reynolds shear stress is more than the compensation by the additional stresses, induced by the solid phase. Oblate particles are found to avoid the region close to the wall, travelling parallel to it with small angular velocities, while preferentially sampling high-speed fluid in the wall region. Prolate particles also tend to orient parallel to the wall and avoid its vicinity. Their reluctance to rotate around the spanwise axis reduces the wall-normal velocity fluctuation of the flow and therefore the turbulence Reynolds stress, similar to oblates; however, they undergo rotations in wall-parallel planes which increase the additional solid stresses due to their relatively larger angular velocities compared to the oblates. These larger additional stresses compensate for the reduction in turbulence activity and lead to a wall drag similar to that of single-phase flows. Spheres on the other hand, form a layer close to the wall with large angular velocities in the spanwise direction, which increases the turbulence activity in addition to exerting the largest solid stresses on the suspension, in comparison to the other studied shapes. Spherical particles therefore increase the wall drag with respect to the single-phase flow.

JFM classification

Flow Control: Drag reduction Multiphase and Particle-laden Flows: Multiphase flow Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 887 - 901
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ardekani, M. N., Costa, P., Breugem, W. P. & Brandt, L. 2016 Numerical study of the sedimentation of spheroidal particles. Intl J. Multiphase Flow 87, 16–34.Google Scholar
Ardekani, M. N., Costa, P., Breugem, W. P., Picano, F. & Brandt, L. 2017 Drag reduction in turbulent channel flow laden with finite-size oblate spheroids. J. Fluid Mech. 816, 43–70.Google Scholar
Breugem, W.-P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231 (13), 4469–4498.Google Scholar
Costa, P., Boersma, B. J., Westerweel, J. & Breugem, W. P. 2015 Collision model for fully resolved simulations of flows laden with finite-size particles. Phys. Rev. E 92 (5), 053012.Google Scholar
Costa, P., Picano, F., Brandt, L. & Breugem, W. P. 2016 Universal scaling laws for dense particle suspensions in turbulent wall-bounded flows. Phys. Rev. Lett. 117, 134501.Google Scholar
Do-Quang, M., Amberg, G., Brethouwer, G. & Johansson, A. V. 2014 Simulation of finite-size fibers in turbulent channel flows. Phys. Rev. E 89 (1), 013006.Google Scholar
Dubief, Y., White, C. M., Terrapon, V. E., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2004 On the coherent drag-reducing and turbulence-enhancing behaviour of polymers in wall flows. J. Fluid Mech. 514, 271–280.Google Scholar
Eshghinejadfard, A., Hosseini, S. A. & Thévenin, D. 2017 Fully-resolved prolate spheroids in turbulent channel flows: a lattice Boltzmann study. AIP Adv. 7 (9), 095007.Google Scholar
Fornari, W., Formenti, A., Picano, F. & Brandt, L. 2016 The effect of particle density in turbulent channel flow laden with finite size particles in semi-dilute conditions. Phys. Fluids 28 (3), 033301.Google Scholar
Jeffrey, D. J. 1982 Low-Reynolds-number flow between converging spheres. Mathematika 29, 58–66.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Lashgari, I., Picano, F., Breugem, W. P. & Brandt, L. 2014 Laminar, turbulent, and inertial shear-thickening regimes in channel flow of neutrally buoyant particle suspensions. Phys. Rev. Lett. 113 (25), 254502.Google Scholar
Loisel, V., Abbas, M., Masbernat, O. & Climent, E. 2013 The effect of neutrally buoyant finite-size particles on channel flows in the laminar-turbulent transition regime. Phys. Fluids 25 (12), 123304.Google Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.Google Scholar
Lundell, F., Söderberg, L. D. & Alfredsson, P. H. 2011 Fluid mechanics of papermaking. Annu. Rev. Fluid Mech. 43, 195–217.Google Scholar
Mansour, N. N., Kim, J. & Moin, P. 1988 Reynolds-stress and dissipation-rate budgets in a turbulent channel flow. J. Fluid Mech. 194, 15–44.Google Scholar
Matas, J. P., Morris, J. F. & Guazzelli, E. 2003 Transition to turbulence in particulate pipe flow. Phys. Rev. Lett. 90 (1), 014501.Google Scholar
Mehta, A. J. 2014 An Introduction to Hydraulics of Fine Sediment Transport. World Scientific.Google Scholar
Naso, A. & Prosperetti, A. 2010 The interaction between a solid particle and a turbulent flow. New J. Phys. 12 (3), 033040.Google Scholar
Picano, F., Breugem, W. P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prosperetti, A. 2015 Life and death by boundary conditions. J. Fluid Mech. 768, 1–4.Google Scholar
Roma, A. M., Peskin, C. S. & Berger, M. J. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153 (2), 509–534.Google Scholar
Tanaka, M. & Teramoto, D. 2015 Modulation of homogeneous shear turbulence laden with finite-size particles. J. Turbul. 16 (10), 979–1010.Google Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for simulation of particulate flow. J. Comput. Phys. 209 (2), 448–476.Google Scholar
Wang, G.2017 Modulation of wall-bounded turbulent flows by large particles: effect of concentration, inertia, and shape. PhD thesis, Dynamique des fluides, Institut National Polytechnique de Toulouse.Google Scholar
Wang, G., Abbas, M. & Climent, E. 2018 Modulation of the regeneration cycle by neutrally buoyant finite-size particles. J. Fluid Mech. 852, 257–282.Google Scholar
Wang, L., Peng, C., Guo, Z. & Yu, Z. 2016 Flow modulation by finite-size neutrally buoyant particles in a turbulent channel flow. Trans. ASME J. Fluids Engng 138 (4), 041306.Google Scholar
Yu, W., Vinkovic, I. & Buffat, M. 2016 Finite-size particles in turbulent channel flow: quadrant analysis and acceleration statistics. J. Turbul. 17 (11), 1048–1071.Google Scholar
Zhang, Q. & Prosperetti, A. 2010 Physics-based analysis of the hydrodynamic stress in a fluid-particle system. Phys. Fluids 22 (3), 033306.Google Scholar