Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T11:02:03.657Z Has data issue: false hasContentIssue false
  • English
  • Français

High-fidelity measurements in channel flow with polymer wall injection

Published online by Cambridge University Press:  26 November 2018

John R. Elsnab Open the ORCID record for John R. Elsnab [Opens in a new window] ,
Jason P. Monty ,
Christopher M. White Open the ORCID record for Christopher M. White [Opens in a new window] ,
Manoochehr M. Koochesfahani  and
Joseph C. Klewicki
John R. Elsnab*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, Vic 3010, Australia
Jason P. Monty
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, Vic 3010, Australia
Christopher M. White
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
Manoochehr M. Koochesfahani
Affiliation:
Department of Mechanical Engineering, Michigan State University, East Lansing, MI 48824, USA
Joseph C. Klewicki
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, Vic 3010, Australia Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Streamwise velocity profiles and their wall-normal derivatives were used to investigate the properties of turbulent channel flow in the low polymer drag reduction 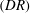$(DR)$ regime (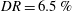$DR=6.5\,\%$ to 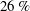$26\,\%$), as realized via polymer injection at the channel surface. Streamwise velocity data were obtained over a friction Reynolds number ranging from 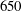$650$ to 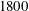$1800$ using the single-velocity-component version of molecular tagging velocimetry (1c-MTV). This adaptation of the MTV technique has the ability to accurately capture instantaneous profiles at very high spatial resolution (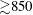${\gtrsim}850$ data points per wall-normal profile), and thus generate well-resolved derivative information as well. Owing to this ability, the present study is able to build upon and extend the recent numerical simulation analysis of White et al. (J. Fluid Mech., vol. 834, 2018, pp. 409–433) that examined the mean dynamical structure of polymer drag-reduced channel flow at friction Reynolds numbers up to 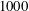$1000$. Consistently, the present mean velocity profiles indicate that the extent of the logarithmic region diminishes with increasing polymer concentration, while statistically significant increases in the logarithmic profile slope begin to occur for drag reductions less than $15\,\%$. Profiles of the r.m.s. streamwise velocity indicate that the maximum moves farther from the wall and increases in magnitude with reductions in drag. Similarly, with increasing drag reduction, the profile of the combined Reynolds and polymer shear stress exhibits a decrease in its maximum value that also moves farther from the wall. Correlations are presented that estimate the location and value of the maximum r.m.s. streamwise velocity and combined Reynolds and polymer shear stress. Over the range of 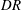$DR$ investigated, these effects consistently exhibit approximately linear trends as a function of 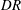$DR$. The present measurements allow reconstruction of the mean momentum balance (MMB) for channel flow, which provides further insights regarding the physics described in the study by White et al. In particular, the present findings support a physical scenario in which the self-similar properties on the inertial domain identified from the leading-order structure of the MMB begin to detectably and continuously vary for drag reductions less than 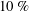$10\,\%$.

JFM classification

Boundary Layers: Boundary layer structure Non-Newtonian Flows: Polymers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 851 - 886
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H., Orlu, R. & Segalini, A. 2012 A new formulation for the streamwise turbulence intensity distribution in wall-bounded turbulent flows. Eur. J. Mech. (B/Fluids) 36, 167–175.Google Scholar
Benzi, R., Angelis, E. D., L’vov, V. S., Procaccia, I. & Tiberkevich, V. 2006 Maximum drag reduction asymptotes and the cross-over to the Newtonian plug. J. Fluid Mech. 551, 185–195.Google Scholar
Berman, N. S. 1978 Drag reduction by polymers. Annu. Rev. Fluid Mech. 10, 47–64.Google Scholar
Bohl, D. G.2002 Experimental study of the 2-D and 3-D structure of a concentrated line vortex. PhD thesis, Michigan State University, East Lansing, Michigan.Google Scholar
Caso, M. & Bohl, D. 2014 Error reduction in molecular tagging velocimetry via image preprocessing. Exp. Fluids 55, 1802–1811.Google Scholar
Castro, I. P., Segalini, A. & Alfredsson, P. H. 2013 Outer-layer turbulence intensities in smooth- and rough-wall boundary layers. J. Fluid Mech. 727, 119–131.Google Scholar
Dubief, Y., Terrapon, V. E. & Soria, J. 2013 On the mechanism of elasto-inertial turbulence. Phys. Fluids 25, 110817.Google Scholar
Dubief, Y., White, C. M., Terrapon, V. E., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2004 On the coherent drag-reducing turbulence-enhancing behaviour of polymers in wall flows. J. Fluid Mech. 514, 271–280.Google Scholar
Ebner, R. L., Mehdi, F. & Klewicki, J. C. 2016 Shared dynamical features of smooth- and rough-wall boundary-layer turbulence. J. Fluid Mech. 792, 435–469.Google Scholar
Elbing, B. R., Perlin, M., Dowling, D. R. & Ceccio, S. L. 2013 Modification of the mean near-wall velocity profile of a high-Reynolds number turbulent boundary layer with the injection of drag-reducing polymer solutions. Phys. Fluids 25, 085103.Google Scholar
Elsnab, J. R., Monty, J. P., White, C. M., Koochesfahani, M. M. & Klewicki, J. C. 2017 Efficacy of single component MTV to measure turbulent wall-flow velocity derivative profiles at high resolution. Exp. Fluids 58, 128–139.Google Scholar
Fife, P., Klewicki, J. & Wei, T. 2009 Time averaging in turbulence settings may reveal an infinite hierarchy of length scales. J. Discrete Continuous Dyn. Syst. 23 (3), 781–807.Google Scholar
Hou, Y. X., Somandepalli, V. S. R. & Mungal, M. G. 2008 Streamwise development of turbulent boundary-layer drag reduction with polymer injection. J. Fluid Mech. 597, 31–66.Google Scholar
Hoyt, J. W. 1991 ‘Negative roughness’ and polymer drag reduction. Exp. Fluids 11, 142–146.Google Scholar
Hyland, R. W. & Wexler, A.1980 Formulations for the thermodynamic properties of the saturated phases of $\text{H}_{2}\text{O}$ from 173.15 K to 473.15 K. Tech. Rep. RP 216, Part 1. ASHRAE.Google Scholar
Kim, K., Islam, M. T., Shen, X., Sirviente, A. I. & Solomon, M. J. 2004 Effect of macromolecular polymer structures on drag reduction in a turbulent channel flow. Phys. Fluids 16, 4150–4162.Google Scholar
Klewicki, J. C. 2013a A description of turbulent wall-flow vorticity consistent with mean dynamics. J. Fluid Mech. 737, 176–204.Google Scholar
Klewicki, J. C. 2013b Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.Google Scholar
Klewicki, J., Ebner, R. & Wu, X. 2011 Mean dynamics of transitional boundary-layer flow. J. Fluid Mech. 682, 617–651.Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Klewicki, J. & Oberlack, M. 2015 Finite Reynolds number properties of a turbulent channel flow similarity solution. Phys. Fluids 27 (9), 095110.Google Scholar
Klewicki, J. C., Fife, P., Wei, T. & McMurtry, P. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. R. Soc. Lond. A 365, 823–839.Google Scholar
Klewicki, J. C., Philip, J., Marusic, I., Chauhan, K. & Morrill-Winter, C. 2014 Self-similarity in the inertial region of wall turbulence. Phys. Rev. E 90, 063015.Google Scholar
Koochesfahani, M. M. & Nocera, D. G. 2007 Molecular tagging velocimetry. Handbook of Experimental Fluid Dynamics, chap. 5.4. Springer.Google Scholar
Lee, J. H., Kevin, M. J. P. & Hutchins, N. 2016 Validating under-resolved turbulence intensities for PIV experiments in canonical wall-bounded turbulence. Exp. Fluids 57, 129–140.Google Scholar
Lighthill, M. J. 1958 On displacement thickness. J. Fluid Mech. 4, 383–392.Google Scholar
Luchik, T. S. & Tiederman, W. G. 1988 Turbulent structure in low-concentration drag-reducing channel flows. J. Fluid Mech. 190, 241–263.Google Scholar
Lumley, J. L. 1969 Drag reduction by additives. Ann. Rev. Fluid Mech. 1, 367–384.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mehdi, F., Klewicki, J. C. & White, C. M. 2013 Mean force structure and its scaling in rough-wall turbulent boundary layers. J. Fluid Mech. 731, 682–712.Google Scholar
Moffat, R. J. 1988 Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1, 3–17.Google Scholar
Monty, J. P. & Chong, M. S. 2009 Turbulent channel flow: comparison of streamwise velocity data from experiments and direct numerical simulation. J. Fluid Mech. 633, 461–474.Google Scholar
Nagashima, A. 1977 Viscosity of water substances: new international formulation and its background. J. Phys. Chem. Ref. Data 6, 1133–1166.Google Scholar
Owolabi, B. E., Dennis, D. J. C. & Poole, R. J. 2017 Turbulent drag reduction by polymer additives in parallel-shear flows. J. Fluid Mech. 827, R4.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge.Google Scholar
Somandepalli, V. S. R., Hou, Y. X. & Mungal, M. G. 2010 Concentration flux measurements in a polymer drag-reduced turbulent boundary layer. J. Fluid Mech. 644, 281–319.Google Scholar
Squire, D. T., Morrill-Winter, C., Hutchins, N., Schultz, M. P., Klewicki, J. C. & Marusic, I. 2016 Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.Google Scholar
Thais, L., Mompean, G. & Gatski, T. B. 2013 Spectral analysis of turbulent viscoelastic and Newtonian channel flows. J. Non-Newtonian Fluid Mech. 200, 165–176.Google Scholar
Thais, L., Tejada-Martinez, A., Gatski, T. B. & Mompean, G. 2011 A massively parallel hybrid scheme for direct numerical simulation of turbulent viscoelastic channel flow. Comput. Fluids 43, 134–142.Google Scholar
Tidederman, W. G., Luchik, T. S. & Bogard, D. G. 1985 Wall-layer structure and drag reduction. J. Fluid Mech. 156, 419–437.Google Scholar
Tirtaatmadja, V., McKinley, G. H. & Cooper-White, J. J. 2006 Drop formation and breakup of low viscosity elastic fluids: effects of molecular weight and concentration. Phys. Fluids 18, 043101.Google Scholar
Toms, B. A. 1948 Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proc. 1st Intl Congr. Rheol. N. Holland, Amsterdam, vol. 2, pp. 135–141. North-Holland.Google Scholar
Virk, P. S. 1975 Drag reduction fundamentals. AICHE J. 21, 625–656.Google Scholar
Walker, D. T. & Tiederman, W. G. 1989 The concentration field in a turbulent channel flow with polymer injection at the wall. Exp. Fluids 8, 86–94.Google Scholar
Walker, D. T. & Tiederman, W. G. 1990 Turbulent structure in a channel flow with polymer injection at the wall. J. Fluid Mech. 218, 377–403.Google Scholar
Walker, D. T., Tiederman, W. G. & Luchik, T. S. 1986 Optimization of the injection process for drag-reducing additives. Exp. Fluids 4, 114–120.Google Scholar
Warholic, M. D., Massah, H & Hanratty, T. J. 1999 Influence of drag-reducing polymers on turbulence: effects of Reynolds number, concentration and mixing. Exp. Fluids 27, 461–472.Google Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Wei, T. & Willmarth, W. W. 1992 Modifying turbulent structure with drag-reducing polymer additives in turbulent channel flows. J. Fluid Mech. 245, 619–641.Google Scholar
White, C. M., Dubief, Y. & Klewicki, J. 2012 Re-examining the logarithmic dependence of the mean velocity distribution in polymer drag reduced wall-bounded flow. Phys. Fluids 12, 021701.Google Scholar
White, C. M., Dubief, Y. & Klewicki, J. 2018 Properties of the mean momentum balance in polymer drag reduced channel flow. J. Fluid Mech. 834, 409–433.Google Scholar
White, C. M. & Mungal, M. G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.Google Scholar
White, C. M., Somandepalli, V. S. R. & Mungal, M. G. 2004 The turbulence structure of drag-reduced boundary layer flow. Exp. Fluids 36, 62–69.Google Scholar
Winkel, E. S., Oweis, G. F., Vanapalli, S. A., Dowling, D. R., Perlin, M., Solomon, M. J. & Ceccio, S. L. 2009 High-Reynolds-number turbulent boundary layer friction drag reduction from wall-injected polymer solutions. J. Fluid Mech. 621, 259–288.Google Scholar
Wu, J. & Tulin, M. P. 1972 Drag reduction by ejecting additive solutions into pure-water boundary layer. Trans. ASME D: J. Basic Engng 94, 749–754.Google Scholar
Zhou, A. & Klewicki, J. 2015 Properties of the streamwise velocity fluctuations in the inertial layer of turbulent boundary layers and their connection to self-similar mean dynamics. Intl J. Heat Fluid Flow 51, 372–382.Google Scholar
Zimm, B. H. 1956 Dynamics of polymer molecules in dilute solution: viscoelasticity, flow birefringence and dielectric loss. J. Chem. Phys. 24, 269–278.Google Scholar