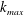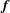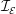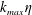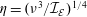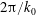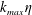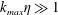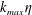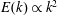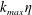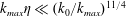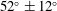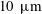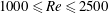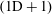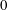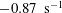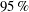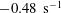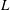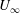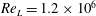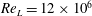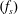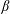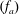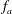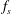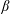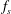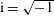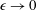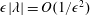We examine the relation between the absolute equilibrium state of the spectrally truncated Euler equations (TEE) predicted by Kraichnan (J. Fluid Mech., vol. 59 (4), 1973, pp. 745–752) to the forced and dissipated flows of the spectrally truncated Navier–Stokes (TNS) equations. In both of these idealized systems, a finite number of Fourier modes is kept contained inside a sphere of radius 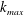$k_{max}$, but, while the first conserves energy, in the second, energy is injected by a body-force 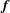$\boldsymbol{f}$ and dissipated by the viscosity $\unicode[STIX]{x1D708}$. 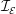For the TNS system, stochastically forced with energy injection rate ${\mathcal{I}}_{{\mathcal{E}}}$, we show, using an asymptotic expansion of the Fokker-Planck equation, that in the limit of small 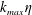$k_{max}\unicode[STIX]{x1D702}$ (where 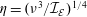$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/{\mathcal{I}}_{{\mathcal{E}}})^{1/4}$, the Kolmogorov length scale) the flow approaches the absolute equilibrium solution of Kraichnan with an effective ‘temperature’ such that there is a balance between the energy injection and the energy dissipation rate. We further investigate the TNS system using direct numerical simulations in periodic cubic boxes of size 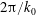$2\unicode[STIX]{x03C0}/k_{0}$. The simulations verify the predictions of the model for small values of $k_{max}\unicode[STIX]{x1D702}$. For intermediate values of 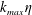$k_{max}\unicode[STIX]{x1D702}$, a transition from the quasi-equilibrium ‘thermal’ state to Kolmogorov turbulence is observed. In particular, we demonstrate that, at steady state, the TNS system reproduces the Kolmogorov energy spectrum if 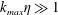$k_{max}\unicode[STIX]{x1D702}\gg 1$. As 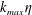$k_{max}\unicode[STIX]{x1D702}$ becomes smaller, then a bottleneck effect appears, taking the form of the equipartition spectrum 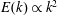$E(k)\propto k^{2}$ at small scales. As 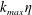$k_{max}\unicode[STIX]{x1D702}$ is decreased even further, so that 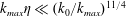$k_{max}\unicode[STIX]{x1D702}\ll (k_{0}/k_{max})^{11/4}$, the equipartition spectrum occupies all scales approaching the asymptotic equilibrium solutions found before. If the forcing is applied at small scales and the dissipation acts only at large scales, then the equipartition spectrum appears at all scales for all values of $\unicode[STIX]{x1D708}$. In both cases, a finite forward or inverse flux is present even for the cases where the flow is close to the equilibrium state solutions. However, unlike the classical turbulence, where an energy cascade develops with a mean energy flux that is large compared to its fluctuations, the quasi-equilibrium state has a mean flux of energy that is subdominant to the large flux fluctuations observed.

We study particle capture on an angled cylinder at a range of Péclet numbers. This system was inspired by the plumose antennae of certain species of male moths that intercept female pheromones at low Péclet numbers of 0.9–23. We use confocal microscopy to measure the branching patterns of 49 moths, spanning 12 families and two orders of magnitude in mass. Among the three levels of hierarchy in antennae, we find the middle level has a prevalent branching angle, $52^{\circ }\pm 12^{\circ }$ across our study set. Such intermediate branching angles are a surprising way to intercept molecules because they do not maximize the exposed surface area. To understand the benefits of angling cylinders into the flow, we study particle collection at high Péclet number using $10~\unicode[STIX]{x03BC}\text{m}$ drops that are several orders of magnitude larger than moth pheromones. Wind tunnel tests show that cylinders angled at $30^{\circ }{-}60^{\circ }$ are optimal for collection of particles, collecting 30 % more than when perpendicular to the flow. Simulations and smoke visualization show that angled cylinders bend incoming streamlines, creating a lingering effect near the cylinder that can enhance deposition by diffusion. We surmise that the optimal angle arises from a trade-off between the lingering effect, which decreases with increasing angle of the cylinder, and the cylinder’s increasing projected area as it is turned more perpendicular to the flow. Using a mathematical model, we show that only cylinders at low Péclet number show improved collection at intermediate angles. Thus, we cannot rationalize the high collection rates in our wind tunnel experiments at high Péclet number. We hope that our study will inspire more research into bio-inspired particle collection of angled surfaces, and find applications in sensors and filters.

We conduct numerical simulations to investigate the formation and evolution of drops and vortex rings of particle-laden fingers in double-diffusive convection in stably stratified environments. We show that the temporal evolution can be divided into double diffusion, acceleration and deceleration phases. The acceleration phase is a result of the vanishing temperature perturbation in the drop during the descent in the layer of uniform temperature. The drop decelerates because it transforms into a vortex ring. A theoretical drag model is presented to predict the speed of the spherical drop with the low drop Reynolds number. By formulating the boundary condition based on the vorticity, our drag model gives a more general form of the drag coefficient for small spherical drops and shows good agreement in predicting the drag coefficient. Drops with five particle sizes are compared, and it is found that although the greater vertical settling enhances vertical transport, the final state differs little among the various sizes. Comparison of our drag model with the simulation results under various bulk conditions and previous experimental results shows good model predictability. Finally, a comparison with the salt-finger case shows that the diffusive nature of the dissolved scalar field, along with the wake effect, can result in an apparent loss of mass from the drop and a permanent presence of the connection between the drop and its parent finger. This makes the observed detachment of the particle-laden drop much less likely in the salt-finger case.

The influence of a horizontal wall on the evolution of the long-wave instability in equal strength counter-rotating vortex pairs is studied with direct numerical simulation. The two vortices descend under mutual induction and interact with a ground plane, as would aircraft trailing vortices in ground effect. Both the linear and nonlinear development of the pair is studied for three initial heights above the wall, representative of three modes of interaction identified by experiment. A study of two vortex core sizes over a range of Reynolds numbers ($1000\leqslant Re\leqslant 2500$) is used to verify parameter independence. The vortex system undergoes complex topological changes in the presence of a wall, with the separation of wall generated vorticity into hairpin-like vortex tongues and axial flow development in the primary pair. The secondary structures are rotated and stretched around the primary vortices, strongly influencing the resultant flow evolution and are comparable with those observed for oblique ring–wall interaction. Of the three modes, the small-amplitude mode shows the formation of four principal tongues per long wavelength of the Crow instability, with the secondary vortex remaining connected. The large-amplitude mode undergoes a re-connective process to form two non-planar secondary vortex structures per wavelength, and a simulation of the large ring mode in its first formation develops six tongues per wavelength. These secondary structures ‘rebound’ from the wall and interact at the symmetry plane prior to dissipation, governing the bending, stretching and trajectory of the primary vortex pair.

We propose the first least-order Galerkin model of an incompressible flow undergoing two successive supercritical bifurcations of Hopf and pitchfork type. A key enabler is a mean-field consideration exploiting the symmetry of the mean flow and the asymmetry of the fluctuation. These symmetries generalize mean-field theory, e.g. no assumption of slow growth rate is needed. The resulting five-dimensional Galerkin model successfully describes the phenomenogram of the fluidic pinball, a two-dimensional wake flow around a cluster of three equidistantly spaced cylinders. The corresponding transition scenario is shown to undergo two successive supercritical bifurcations, namely a Hopf and a pitchfork bifurcation on the way to chaos. The generalized mean-field Galerkin methodology may be employed to describe other transition scenarios.

When a container with two distinct fluids is subjected to vibrations in microgravity, the interface may undergo a variety of instabilities and develop towards a complex structure, as seen in recent parabolic flight experiments using both miscible and immiscible liquids. Among other things, the selected pattern depends on the frequency and amplitude of the forcing and, crucially, on its orientation with respect to the initial interface. In a parabolic flight experiment, this initial orientation is largely determined by the stage of the parabolic manoeuvre when the forcing is started and the residual gravity level during the period of microgravity. It plays a key role in the appearance of defects and irregularities during the evolution of the interface triggered by the frozen wave instability. Using numerical simulations, we systematically investigate the effect of initial interface orientation on pattern selection in microgravity for both miscible and immiscible fluids, and compare to available experiments. When the interface and the forcing are nearly aligned, the frozen wave instability is dominant, leading to the development of approximately regular columnar patterns. As the initial angle becomes more oblique, the frozen wave growth becomes more irregular and asymmetric and may involve thin auxiliary columns. Sufficiently large angles suppress the frozen wave instability and, depending on the container aspect ratio, may result in a simple two-column final state.

Most network models describing solute transport in the brain microcirculation use the well-mixed hypothesis and assume that radial gradients inside the blood vessels are negligible. Recent experimental data suggest that these gradients, which may result from heterogeneities in the velocity field or consumption in the tissue, may in fact be important. Here, we study the validity of the well-mixed hypothesis in network models of solute transport using theoretical and computational approaches. We focus on regimes of weak coupling where the transport problem inside the vasculature is independent of the concentration field in the tissue. In these regimes, the boundary condition between vessels and tissue can be modelled by a Robin boundary condition. For this boundary condition and for a single cylindrical capillary, we derive a one-dimensional cross-section average transport problem with dispersion and exchange coefficients capturing the effects of radial gradients. We then extend this model to a network of connected tubes and solve the problem in a complex anatomical network. By comparing with results based on the well-mixed hypothesis, we find that dispersive effects are a fundamental component of transport in transient situations with relatively rapid injections, i.e. frequencies above one Hertz. For slowly varying signals and steady states, radial gradients also significantly impact the spatial distribution of vessel/tissue exchange for molecules that easily cross the blood brain barrier. This suggests that radial gradients cannot be systematically neglected and that there is a crucial need to determine the impact of spatio-temporal heterogeneities on transport in the brain microcirculation.

This paper examines experimentally the dispersion and stability of weakly nonlinear waves on opposing linearly vertically sheared current profiles (with constant vorticity). Measurements are compared against predictions from the unidirectional $(1\text{D}+1)$ constant vorticity nonlinear Schrödinger equation (the vor-NLSE) derived by Thomas et al. (Phys. Fluids, vol. 24, no. 12, 2012, 127102). The shear rate is negative in opposing currents when the magnitude of the current in the laboratory reference frame is negative (i.e. opposing the direction of wave propagation) and reduces with depth, as is most commonly encountered in nature. Compared to a uniform current with the same surface velocity, negative shear has the effect of increasing wavelength and enhancing stability. In experiments with a regular low-steepness wave, the dispersion relationship between wavelength and frequency is examined on five opposing current profiles with shear rates from $0$ to $-0.87~\text{s}^{-1}$. For all current profiles, the linear constant vorticity dispersion relation predicts the wavenumber to within the $95\,\%$ confidence bounds associated with estimates of shear rate and surface current velocity. The effect of shear on modulational instability was determined by the spectral evolution of a carrier wave seeded with spectral sidebands on opposing current profiles with shear rates between $0$ and $-0.48~\text{s}^{-1}$. Numerical solutions of the vor-NLSE are consistently found to predict sideband growth to within two standard deviations across repeated experiments, performing considerably better than its uniform-current NLSE counterpart. Similarly, the amplification of experimental wave envelopes is predicted well by numerical solutions of the vor-NLSE, and significantly over-predicted by the uniform-current NLSE.

Large-eddy simulations for the case of an axisymmetric body of revolution with appendages are considered. The geometry is the benchmark case of the DARPA suboff body. The paper focuses on the effects of the Reynolds number on the structure of the boundary layer in the stern area as well as the near wake. For this purpose we compare results for two Reynolds numbers (based on the length of the body, $L$, and the free-stream velocity, $U_{\infty }$): $Re_{L}=12\times 10^{6}$ and $Re_{L}=1.2\times 10^{6}$. Results are in good agreement with published experiments at the same Reynolds numbers. The boundary layer thickness over the stern increases substantially at both simulated Reynolds numbers, due to the adverse pressure gradient at the rear of the body. However, for the high Reynolds number case, a weaker peak of turbulent kinetic energy develops in the outer layer over the stern. Nonetheless, the associated bimodal distribution of the turbulent stresses in the wake is already very similar a few diameters downstream of the tail. First- and second-order moments demonstrate that junction vortices at the stern bring higher velocities and turbulence at the root of the appendages for both Reynolds numbers, with a more evident signature at $Re_{L}=12\times 10^{6}$. An azimuthal readjustment of turbulent kinetic energy occurs in the wake, becoming more axisymmetric, with increasing values in the planes aligned with the stern appendages, due to turbulence coming from both the stern boundary layer and junction vortices.

The vortex sound interaction in acoustic resonance induced by vortex shedding from a cylinder in a flow duct is numerically studied based on a nonlinear physical model, which consists of three meshless sub-models describing the vortex shedding, sound generation and propagation within the duct. In addition, the acoustic particle velocity near the separation point of the shear layer is solved and added onto the Kutta condition of the vortex shedding, which takes the acoustic feedback effect into consideration and makes the vortex sound interaction bi-directional. The predicted results of resonant frequency and amplitude are found to be in conformity with previous experiment data, especially, a continuous description of the onset–sustain–cease of lock-in phenomenon is well captured. The lock-in phenomenon is depicted as a vigorous competition between the vortex shedding frequency $(f_{s})$ and the inherent frequency of the acoustic $\unicode[STIX]{x1D6FD}$-mode $(f_{a})$. The mutual capturing behaviour of these two frequencies is dominated by $f_{a}$. Moreover, $f_{s}$ cannot always be locked onto $f_{a}$ within the whole lock-in region, which is in marked contrast to the previous understanding. In this aspect, two lock-in regions, the synchronous region and the $\unicode[STIX]{x1D6FD}$-mode dominant region, are defined according to the relevance of $f_{s}$ and $f_{a}$. The maximum resonant sound appears at the end of the synchronous region. The present model not only predicts the proper characteristics of frequency lock-in as observed in experiments, but also helps to provide a more detailed understanding of the underlying lock-in mechanism.

In this article, we investigate the internal dynamics (velocity profiles and shear rate) of free-surface surges made of viscoplastic fluids. Compared with fluids without a yield stress, additional complexity arises from the possible coexistence of sheared and unsheared (or pseudo-plug) zones in the flow. Expanding on the thin-layer approach of Fernandez-Nieto et al. (J. Non-Newtonian Fluid Mech., vol. 165, 2010, pp. 712–732), we derive formal asymptotic expansions of the velocity field and discharge up to $O(\unicode[STIX]{x1D716})$ with respect to flow aspect ratio $\unicode[STIX]{x1D716}$. Detailed comparisons between these theoretical predictions and experimental data reveal that, although the leading-order approximation (equivalent to a lubrication model) satisfactorily accounts for the global dynamics of the flow, considering $O(\unicode[STIX]{x1D716})$ correction terms is required to capture the evolution of velocity and shear rate close to the tip. Notably, these correction terms are responsible for the vanishing of the unsheared layer in the tip region, a feature clearly observed in the experiments. Differences between the leading-order and $O(\unicode[STIX]{x1D716})$ models appear to be enhanced by the viscoplastic character of the fluid. In particular, $O(\unicode[STIX]{x1D716})$ correction terms related to the existence of $O(1)$ plastic normal stresses in the pseudo-plug layer play a critical role. This study provides important insights for future development of consistent shallow-water models adapted to viscoplastic materials.

Asymptotic approximations are derived for the hydrodynamic force on a rigid, axisymmetric slender particle executing longitudinal or transverse oscillation in unsteady Stokes flow. The slender particle has an aspect ratio $\unicode[STIX]{x1D716}=a/\ell \ll 1$, where $\ell$ is the half-length of the particle, and $a$ is its characteristic cross-sectional width. It is assumed that the particle has zero thickness at its ends. The frequency of oscillation is parameterized by the complex quantity $\unicode[STIX]{x1D706}^{2}=-\text{i}\ell ^{2}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D708}$, where $\unicode[STIX]{x1D708}$ is the kinematic viscosity, $\unicode[STIX]{x1D714}$ is the particle angular oscillation frequency (units of radians per second) and $\text{i}=\sqrt{-1}$. Asymptotic approximations for the force are obtained in three distinguished limits for longitudinal oscillations: (i) a ‘low-frequency’ regime with $\unicode[STIX]{x1D716}\rightarrow 0$ and $|\unicode[STIX]{x1D706}|$ fixed; (ii) a ‘moderate-frequency’ regime with $\unicode[STIX]{x1D716}\rightarrow 0$ and $\unicode[STIX]{x1D716}|\unicode[STIX]{x1D706}|=O(1)$; and (iii) a ‘high-frequency’ regime with $\unicode[STIX]{x1D716}\rightarrow 0$ and $\unicode[STIX]{x1D716}|\unicode[STIX]{x1D706}|=O(1/\unicode[STIX]{x1D716}^{2})$. The acceleration reaction is a leading-order contributor to the force in this last regime, whereas it is subdominant at moderate frequency. For transverse oscillation we construct asymptotic approximations in the low and moderate-frequency regimes. Here, the acceleration reaction here plays a leading-order role at moderate frequency; hence, a ‘high frequency’ regime in this case simply corresponds to the limiting behaviour for $\unicode[STIX]{x1D716}|\unicode[STIX]{x1D706}|\gg 1$. Our asymptotic predictions are in good agreement with the numerically computed frequency-dependent force on a prolate spheroid ($\unicode[STIX]{x1D716}=0.1$) for longitudinal and transverse oscillations by Lawrence and Weinbaum (J. Fluid Mech., vol. 189, 1988, pp. 463–489) and Pozrikidis (Phys. Fluids, vol. 1, 1989a, pp. 1508–1520), respectively.

An asymptotic model is derived for the competitive diffusion-limited evaporation of multiple thin sessile droplets under the assumption that the droplets are well separated. Exact solutions of the model are obtained for a pair of and for a polygonal array of identical droplets, and the model is found to perform well even outside its formal range of validity, up to and including the limit of touching droplets. The shielding effect of droplets on each other is demonstrated, and the model is used to investigate the effect of this shielding on droplet evolutions and lifetimes, as well as on the coffee-ring effect. The theoretical predictions of the model are found to be in good agreement with recent experimental results for seven relatively closely spaced droplets, suggesting that the model could be a useful tool for studying a wide range of other droplet configurations.

In this study, we assess the veracity of models for density-weighted local flame displacement speed of turbulent premixed flames. It will be shown that a combination of two models, one for the weakly stretched laminar flame state and another derived for a configuration where a curved laminar flame interacts with itself to annihilate, can describe most local realizations of a turbulent premixed flame. To that end, we have performed direct numerical simulations of a reactive mixture of hydrogen–air at atmospheric pressure using a detailed chemical reaction mechanism and analysed the dataset with recently developed flame particle tracking techniques. Forward tracking a large number of flame particles from the generating locations of the corresponding flame surfaces (given by backward tracking) to the corresponding annihilating locations, creates a manifold of local states that can represent nearly all possible states realizable for the turbulent premixed flame under consideration. With all the states of the flame accessible over time, we first assess the applicability of the two-parameter Markstein length based flame speed model. It is found that the model prediction is reasonably accurate for a significant part of the flame particles’ lifetime, for turbulent premixed flames with Karlovitz number $O(10)$. However, during the final stage of annihilation of the flame particles in the negatively curved trailing regions, the local structure of the flame no longer resembles a standard premixed flame, even qualitatively. A new interaction model for the flame displacement speed, during these final stages of annihilation of the flame elements, has been derived.