Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T20:16:41.277Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study of dispersion and modulational instability of surface gravity waves on constant vorticity currents

Published online by Cambridge University Press:  17 December 2019

James N. Steer Open the ORCID record for James N. Steer [Opens in a new window] ,
Alistair G. L. Borthwick Open the ORCID record for Alistair G. L. Borthwick [Opens in a new window] ,
Dimitris Stagonas ,
Eugeny Buldakov Open the ORCID record for Eugeny Buldakov [Opens in a new window]  and
Ton S. van den Bremer Open the ORCID record for Ton S. van den Bremer [Opens in a new window]
James N. Steer*
Affiliation:
School of Engineering, University of Edinburgh, EdinburghEH9 3FB, UK Wind and Marine Energy Systems CDT, University of Strathclyde, GlasgowG1 1XW, UK
Alistair G. L. Borthwick
Affiliation:
School of Engineering, University of Edinburgh, EdinburghEH9 3FB, UK
Dimitris Stagonas
Affiliation:
School of Water, Energy and Environment, Cranfield University, CranfieldMK43 0AL, UK
Eugeny Buldakov
Affiliation:
Department of Civil, Environmental and Geomatic Engineering, University College London, Chadwick Building, LondonWC1 6BT, UK
Ton S. van den Bremer
Affiliation:
Department of Engineering Science, University of Oxford, OxfordOX1 3PJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper examines experimentally the dispersion and stability of weakly nonlinear waves on opposing linearly vertically sheared current profiles (with constant vorticity). Measurements are compared against predictions from the unidirectional $(1\text{D}+1)$ constant vorticity nonlinear Schrödinger equation (the vor-NLSE) derived by Thomas et al. (Phys. Fluids, vol. 24, no. 12, 2012, 127102). The shear rate is negative in opposing currents when the magnitude of the current in the laboratory reference frame is negative (i.e. opposing the direction of wave propagation) and reduces with depth, as is most commonly encountered in nature. Compared to a uniform current with the same surface velocity, negative shear has the effect of increasing wavelength and enhancing stability. In experiments with a regular low-steepness wave, the dispersion relationship between wavelength and frequency is examined on five opposing current profiles with shear rates from $0$ to $-0.87~\text{s}^{-1}$. For all current profiles, the linear constant vorticity dispersion relation predicts the wavenumber to within the $95\,\%$ confidence bounds associated with estimates of shear rate and surface current velocity. 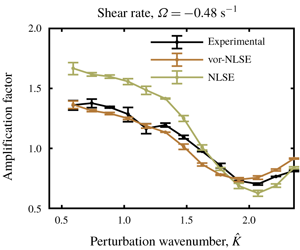The effect of shear on modulational instability was determined by the spectral evolution of a carrier wave seeded with spectral sidebands on opposing current profiles with shear rates between $0$ and $-0.48~\text{s}^{-1}$. Numerical solutions of the vor-NLSE are consistently found to predict sideband growth to within two standard deviations across repeated experiments, performing considerably better than its uniform-current NLSE counterpart. Similarly, the amplification of experimental wave envelopes is predicted well by numerical solutions of the vor-NLSE, and significantly over-predicted by the uniform-current NLSE.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A40
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. G. & McIntyre, M. E. 1978 On wave-action and its relatives. J. Fluid Mech. 89 (4), 647–664.CrossRefGoogle Scholar
Baddour, R. E. & Song, S. 1990a On the interaction between waves and currents. Ocean Engng 17 (1–2), 1–21.CrossRefGoogle Scholar
Baddour, R. E. & Song, S. W. 1990b Interaction of higher-order water waves with uniform currents. Ocean Engng 17 (6), 551–568.CrossRefGoogle Scholar
Baumstein, A. I. 1998 Modulation of gravity waves with shear in water. Stud. Appl. Maths 100 (4), 365–390.CrossRefGoogle Scholar
Benjamin, T. B. & Feir, J. E. 1967 The disintegration of wave trains on deep water. Part 1. Theory. J. Fluid Mech. 27 (3), 417–430.CrossRefGoogle Scholar
Biésel, F. 1950 Etude théorique de la houle en eau courante. La Houille Blanche No. spécial A, 279–285.CrossRefGoogle Scholar
Bretherton, F. P. & Garrett, C. J. R. 1968 Wavetrains in inhomogeneous moving media. Proc. R. Soc. Lond. A 302 (1471), 529–554.Google Scholar
Chabchoub, A., Hoffmann, N., Onorato, M. & Akhmediev, N. 2012 Super rogue waves: observation of a higher-order breather in water waves. Phys. Rev. X 2 (1), 011015.Google Scholar
Chabchoub, A., Hoffmann, N. P. & Akhmediev, N. 2011 Rogue wave observation in a water wave tank. Phys. Rev. Lett. 106 (20), 204502.CrossRefGoogle Scholar
Choi, W. 2009 Nonlinear surface waves interacting with a linear shear current. Math. Comput. Simulat. 80 (1), 29–36.CrossRefGoogle Scholar
Constantin, A. & Strauss, W. 2004 Exact steady periodic water waves with vorticity. Commun. Pure Appl. Maths 57 (4), 481–527.CrossRefGoogle Scholar
Craik, A. D. D. 1988 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Da Silva, A. F. T. & Peregrine, D. H. 1988 Steep, steady surface waves on water of finite depth with constant vorticity. J. Fluid Mech. 195, 281–302.CrossRefGoogle Scholar
Dalrymple, R. A. 1974 A finite amplitude wave on a linear shear current. J. Geophys. Res. 79 (30), 4498–4504.CrossRefGoogle Scholar
Dalrymple, R. A. 1977 A numerical model for periodic finite amplitude waves on a rotational fluid. J. Comput. Phys. 24 (1), 29–42.CrossRefGoogle Scholar
Dysthe, K. B. 1979 Note on a modification to the nonlinear Schrodinger equation for application to deep water waves. Proc. R. Soc. Lond. A 369, 105–114.CrossRefGoogle Scholar
Ellingsen, S. Å & Brevik, I. 2014 How linear surface waves are affected by a current with constant vorticity. Eur. J. Phys. 35 (2), 025005.CrossRefGoogle Scholar
Ellingsen, S. Å. & Li, Y. 2017 Approximate dispersion relations for waves on arbitrary shear flows. J. Geophys. Res. 122 (12), 9889–9905.CrossRefGoogle Scholar
Fermi, E., Pasta, P., Ulam, S. & Tsingou, M.1955 Studies of the nonlinear problems. Tech. Rep. Los Alamos Scientific Lab., N. Mex.CrossRefGoogle Scholar
Ford, J. 1992 The fermi-pasta-ulam problem: paradox turns discovery. Phys. Rep. 213 (5), 271–310.CrossRefGoogle Scholar
Goda, Y. & Suzuki, T. 1976 Estimation of incident and reflected waves in random wave experiments. In 15th International Conference on Coastal Engineering, pp. 828–845.Google Scholar
Groeneweg, J. & Klopman, G. 1998 Changes of the mean velocity profiles in the combined wave–current motion described in a glm formulation. J. Fluid Mech. 370, 271–296.CrossRefGoogle Scholar
Hasimoto, H. & Ono, H. 1972 Nonlinear modulation of gravity waves. J. Phys. Soc. Japan 33 (3), 805–811.CrossRefGoogle Scholar
Henry, D. 2013 On the pressure transfer function for solitary water waves with vorticity. Math. Ann. 357 (1), 23–30.CrossRefGoogle Scholar
Henry, D. & Thomas, G. P. 2017 Prediction of the free-surface elevation for rotational water waves using the recovery of pressure at the bed. Phil. Trans. R. Soc. Lond. A 376 (2111), 20170102.Google Scholar
Hughes, S. A. 1993 Physical Models and Laboratory Techniques in Coastal Engineering, vol. 7. World Scientific.CrossRefGoogle Scholar
Janssen, P. A. E. M. 1981 Modulational instability and the Fermi-Pasta-Ulam recurrence. Phys. Fluids 24 (1), 23–26.CrossRefGoogle Scholar
Jonsson, I. G., Brink-Kjaer, O. & Thomas, G. P. 1978 Wave action and set-down for waves on a shear current. J. Fluid Mech. 87 (3), 401–416.CrossRefGoogle Scholar
Kimmoun, O., Hsu, H. C., Branger, H., Li, M. S., Chen, Y. Y., Kharif, C., Onorato, M., Kelleher, E. J. R., Kibler, B., Akhmediev, N. et al. 2016 Modulation instability and phase-shifted fermi-pasta-ulam recurrence. Sci. Rep.-UK 6, 28516.Google ScholarPubMed
Kirby, J. T. & Chen, T. 1989 Surface waves on vertically sheared flows: approximate dispersion relations. J. Geophys. Res.-Oceans 94 (C1), 1013–1027.CrossRefGoogle Scholar
Klopman, G.1994 Vertical structure of the flow due to waves and currents-laser-doppler flow measurements for waves following or opposing a current. WL Report H840-30, Part II, for Rijkswaterstaat.Google Scholar
Lake, B. M., Yuen, H. C., Rungaldier, H. & Ferguson, W. E. 1977 Nonlinear deep-water waves: theory and experiment. Part 2. Evolution of a continuous wave train. J. Fluid Mech. 83, 49–74.CrossRefGoogle Scholar
Lo, E. & Mei, C. C. 1985 A numerical study of water-wave modulation based on a higher-order nonlinear Schrödinger equation. J. Fluid Mech. 150, 395–416.CrossRefGoogle Scholar
Ma, Y.-C. 1979 The perturbed plane-wave solutions of the cubic Schrödinger equation. Stud. Appl. Maths 60 (1), 43–58.CrossRefGoogle Scholar
Mallory, J. K. 1974 Abnormal waves on the south east coast of South Africa. Int. Hydrogr. Rev. 51 (2), 99–129.Google Scholar
Marine Accident Investigation Branch2016 Report on the investigation of the capsize and sinking of the cement carrier cemfjord in the pentland firth, scotland. Tech. Rep. Marine Accident Investigation Branch.Google Scholar
Melville, W. K. 1982 The instability and breaking of deep-water waves. J. Fluid Mech. 115, 165–185.CrossRefGoogle Scholar
Onorato, M., Proment, D. & Toffoli, A. 2011 Triggering rogue waves in opposing currents. Phys. Rev. Lett. 107 (18), 184502.CrossRefGoogle ScholarPubMed
Peregrine, D. H. 1976 Interaction of water waves and currents. In Adv. Appl. Mech., vol. 16, pp. 9–117. Elsevier.Google Scholar
Peregrine, D. H. & Jonsson, I. G.1983 Interaction of waves and currents. Tech. Rep. University of Bristol.CrossRefGoogle Scholar
Quinn, B. E., Toledo, Y. & Shrira, V. I. 2017 Explicit wave action conservation for water waves on vertically sheared flows. Ocean Model. 112, 33–47.CrossRefGoogle Scholar
Santo, H., Taylor, P. H., Eatock, T. R. & Choo, Y. S. 2013 Average properties of the largest waves in Hurricane Camille. J. Offshore Mech. Arct. 135, 011602.CrossRefGoogle Scholar
Segur, H., Henderson, D., Carter, J., Hammack, J., Li, C.-M., Pheiff, D. & Socha, K. 2005 Stabilizing the Benjamin–Feir instability. J. Fluid Mech. 539, 229–271.CrossRefGoogle Scholar
Shrira, V. I. & Slunyaev, A. V. 2014 Trapped waves on jet currents: asymptotic modal approach. J. Fluid Mech. 738, 65–104.CrossRefGoogle Scholar
Skop, R. A. 1987 Approximate dispersion relation for wave-current interactions. J. Waterw. Port Coast. 113 (2), 187–195.CrossRefGoogle Scholar
Stagonas, D., Buldakov, E. & Simons, R. 2014 Focusing unidirectional wave groups on finite water depth with and without currents. In Thirty-fourth International Conference on Coast. Engng (ed. Lynett, P. J.), pp. 1–6. Coastal Engineering Research Council.Google Scholar
Stewart, R. H. & Joy, J. W. 1974 Hf radio measurements of surface currents. Deep-Sea Res. 21, 1039–1049.Google Scholar
Swan, C., Cummins, I. P. & James, R. L. 2001 An experimental study of two-dimensional surface water waves propagating on depth-varying currents. Part 1. Regular waves. J. Fluid Mech. 428, 273–304.CrossRefGoogle Scholar
Swan, C. & James, R. L. 2000 A simple analytical model for surface water waves on a depth-varying current. Appl. Ocean Res. 22 (6), 331–347.CrossRefGoogle Scholar
Taha, T. R. & Ablowitz, M. I. 1984 Analytical and numerical aspects of certain nonlinear evolution equations. II. Numerical, nonlinear Schrödinger equation. J. Comput. Phys. 55 (2), 203–230.CrossRefGoogle Scholar
Thomas, G. P. 1990 Wave–current interactions: an experimental and numerical study. Part 2. Nonlinear waves. J. Fluid Mech. 216, 505–536.CrossRefGoogle Scholar
Thomas, R., Kharif, C. & Manna, M. 2012 A nonlinear Schrödinger equation for water waves on finite depth with constant vorticity. Phys. Fluids 24 (12), 127102.CrossRefGoogle Scholar
Thompson, P. D. 1949 The propagation of small surface disturbances through rotational flow. Ann. N.Y. Acad. Sci. 51 (1), 463–474.CrossRefGoogle Scholar
Toffoli, A., Waseda, T., Houtani, H., Cavaleri, L., Greaves, D. & Onorato, M. 2015 Rogue waves in opposing currents: an experimental study on deterministic and stochastic wave trains. J. Fluid Mech. 769, 277–297.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1996 Periodic waves with constant vorticity in water of infinite depth. IMA J. Appl. Math. 56 (3), 207–217.CrossRefGoogle Scholar
Weideman, J. A. C. & Herbst, B. M. 1986 Split-step methods for the solution of the nonlinear Schrödinger equation. SIAM J. Numer. Anal. 23 (3), 485–507.CrossRefGoogle Scholar
Whitham, G. B. 1965 A general approach to linear and non-linear dispersive waves using a Lagrangian. J. Fluid Mech. 22 (2), 273–283.CrossRefGoogle Scholar
Yuen, H. C. & Lake, B. M. 1982 Nonlinear dynamics of deep-water gravity waves. In Adv. Appl. Mech., vol. 22, pp. 67–229. Elsevier.Google Scholar