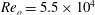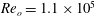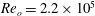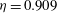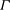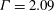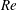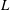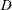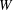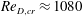The collision between aqueous drops in air typically leads to coalescence after impact. Rebounding of the droplets with similar sizes at atmospheric conditions is not generated, unless with significantly large pressure or high impact parameters exhibiting near-grazing collision. Here we demonstrate experimentally the creation of a non-coalescent regime through addition of a small amount of water-soluble surfactant. We perform a direct simulation to account for the continuum and short-range flow dynamics of the approaching interfaces, as affected by the soluble surfactant. Based on the immersed-boundary formulation, a conservative scheme is developed for solving the coupled surface-bulk convection–diffusion concentration equations, which presents excellent mass preservation in the solvent as well as conservation of total surfactant mass. We show that the Marangoni effect, caused by non-uniform distributions of surfactant on the droplet surface and surface tension, induces stresses that oppose the draining of gas in the interstitial gap, and hence prohibits merging of the interfaces. In such gas–liquid systems, the repulsion caused by the addition of surfactant, as frequently observed in liquid–liquid systems such as emulsions in the form of an electric double-layer force, was found to be too weak to dominate in the attainable range of interfacial separation distances. These results thus identify the key mechanisms governing the impact dynamics of surfactant-coated droplets in air and imply the potential of using a small amount of surfactant to manipulate impact outcomes, for example, to prevent coalescence between droplets or interfaces in gases.

The water entry of a rectangular plate with a high horizontal velocity component is investigated experimentally. The test conditions are representative of those encountered by aircraft during emergency landing on water and are given in terms of three main parameters: horizontal velocity, approach angle, i.e. vertical to horizontal velocity ratio, and pitch angle. Experimental data are presented in terms of pressure, spray root shape, pressure peak propagation velocity and total loads acting on the plate. A theoretical solution of the plate entry problem based on two-dimensional and potential flow assumptions is derived and is used to support the interpretation of the experimental measurements. The results indicate that, as the plate penetrates and the ratio between the plate breadth and the wetted length measured on the longitudinal plane diminishes, the role of the third dimension becomes dominant. The increased possibility for the liquid to escape from the lateral sides yields a reduction of the pressure peak propagation velocity and, consequently, of the corresponding pressure peak intensity. In particular, it is shown that, at the beginning of the entry process, the pressure peak moves much faster than the geometric intersection between the body and the free surface, but at a later stage the two points move along the body at the same speed. Furthermore, it is shown that the spray root develops a curved shape which is almost independent of the specific test conditions, even though the initial growth rate of the curvature is higher for larger pitch angles. The loads follow a linear increase versus time, as predicted by the theoretical model, only in a short initial stage. Next, for all test conditions examined here, they approach a square-root dependence on time. It is seen that, if the loads are scaled by the square of the velocity component normal to the plate, the data are almost independent of the test conditions.

A series of direct numerical simulations were performed of Taylor–Couette (TC) flow, the flow between two coaxial cylinders, with the outer cylinder rotating and the inner one fixed. Three cases were considered, where the Reynolds number of the outer cylinder was $Re_{o}=5.5\times 10^{4}$, $Re_{o}=1.1\times 10^{5}$ and $Re_{o}=2.2\times 10^{5}$. The ratio of radii ${\it\eta}=r_{i}/r_{o}$ was fixed to ${\it\eta}=0.909$ to mitigate the effects of curvature. Axially periodic boundary conditions were used, with the aspect ratio of vertical periodicity ${\it\Gamma}$ fixed to ${\it\Gamma}=2.09$. Being linearly stable, TC flow with outer cylinder rotation is known to have very different behaviour than TC flow with pure inner cylinder rotation. Here, we find that the flow nonetheless becomes turbulent, but the torque required to drive the cylinders and level of velocity fluctuations was found to be smaller than those for pure inner cylinder rotation at comparable Reynolds numbers. The mean angular momentum profiles showed a large gradient in the bulk, instead of the constant angular momentum profiles of pure inner cylinder rotation. The near-wall mean and fluctuation velocity profiles were found to coincide only very close to the wall, showing large deviations from both pure inner cylinder rotation profiles and the classic von Karman law of the wall elsewhere. Finally, transport of angular velocity was found to occur mainly through intermittent bursts, and not through wall-attached large-scale structures as is the case for pure inner cylinder rotation.

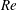TriGlobal linear instability analysis and direct numerical simulations have been performed to unravel the mechanisms ultimately responsible for transition of steady laminar flow over a long rectangular finite-span open cavity with dimensions $L$ : $D$ : $W$$=$ 6 : 1 : 2 to unsteadiness. The steady laminar three-dimensional flow loses stability at $\mathit{Re}_{D,cr}\approx 1080$ as a consequence of linear amplification of a travelling eigenmode that is qualitatively analogous to the shear-layer mode known from analyses of flow in spanwise-periodic cavities, but has a three-dimensional structure which is strongly influenced by the cavity lateral walls. Differences in the eigenspectrum of the present and the spanwise homogeneous flow configuration are documented. Topological changes exerted on the steady laminar flow by linear amplification of the unstable shear-layer mode are reminiscent of observations in experiments at an order of magnitude higher Reynolds number.

Impulsively started, low-aspect-ratio elliptical flat plates have been investigated experimentally to understand the vortex pinch-off dynamics at transitional and fully turbulent Reynolds numbers. The range of Reynolds numbers investigated is representative of those observed in animals that employ rowing and paddling modes of drag-based propulsion and manoeuvring. Elliptical flat plates with five aspect ratios ranging from one to two have been considered, as abstractions of propulsor planforms found in nature. It has been shown that Reynolds-number scaling is primarily determined by plate aspect ratio in terms of both drag forces and vortex pinch-off. Due to vortex-ring growth time scales that are longer than those associated with the development of flow instabilities, the scaling of drag is Reynolds-number-dependent for the aspect-ratio-one flat plate. With increasing aspect ratio, the Reynolds-number dependency decreases as a result of the shorter growth time scales associated with high-aspect-ratio elliptical vortex rings. Large drag peaks are observed during early-stage vortex growth for the higher-aspect-ratio flat plates. The collapse of these peaks with Reynolds number provides insight into the evolutionary convergence process of propulsor planforms used in drag-based swimming modes over diverse scales towards aspect ratios greater than one.

The generation of indirect combustion noise by compositional inhomogeneities is examined theoretically. For this, the compact-nozzle theory of Marble & Candel (J. Sound Vib., vol. 55 (2), 1977, pp. 225–243) is extended to a multi-component gas mixture, and the chemical potential function is introduced as an additional acoustic source mechanism. Transfer functions for subcritical and supercritical nozzle flows are derived, and the contribution of compositional noise is compared to entropy noise and direct noise by considering an idealized nozzle downstream of the combustor exit. It is shown that compositional noise is dependent on the local mixture composition and can exceed entropy noise for fuel-lean conditions and supercritical nozzle flows. This suggests that the compositional indirect noise requires potential consideration with the implementation of low-emission combustors.

Internal phoretic flows due to the interactions of solid boundaries with local chemical gradients may be created using chemical patterning. Alternatively, we demonstrate here that internal flows might also be induced by geometric asymmetries of chemically homogeneous surfaces. We characterise the circulatory flow created in a cavity enclosed between two eccentric cylindrical walls of uniform chemical activity. Local gradients of the diffusing solute induce a slip flow along the surface of the cylinders, leading to a circulatory bulk flow pattern which can be solved analytically in the diffusive limit. The flow strength can be controlled by adjusting the relative positions of the cylinders, and an optimal configuration is identified. These results provide a model system for tunable phoretic pumps.

We consider dynamo action driven by three-dimensional rotating anelastic convection in a spherical shell. Motivated by the behaviour of the solar dynamo, we examine the interaction of hydromagnetic modes with different symmetries and demonstrate how complicated interactions between convection, differential rotation and magnetic fields may lead to modulation of the basic cycle. For some parameters, type 1 modulation occurs by the transfer of energy between modes of different symmetries with little change in the overall amplitude; for other parameters, the modulation is of type 2, where the amplitude is significantly affected (leading to grand minima in activity) without significant changes in symmetry. Most importantly, we identify the presence of ‘supermodulation’ in the solutions, where the activity switches chaotically between type 1 and type 2 modulation; this is believed to be an important process in solar activity.