Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Taira, Kunihiko
Brunton, Steven L.
Dawson, Scott T. M.
Rowley, Clarence W.
Colonius, Tim
McKeon, Beverley J.
Schmidt, Oliver T.
Gordeyev, Stanislav
Theofilis, Vassilios
and
Ukeiley, Lawrence S.
2017.
Modal Analysis of Fluid Flows: An Overview.
AIAA Journal,
Vol. 55,
Issue. 12,
p.
4013.
Sun, Yiyang
Taira, Kunihiko
Cattafesta, Louis N.
and
Ukeiley, Lawrence S.
2017.
Biglobal instabilities of compressible open-cavity flows.
Journal of Fluid Mechanics,
Vol. 826,
Issue. ,
p.
270.
Picella, F.
Loiseau, J.-Ch.
Lusseyran, F.
Robinet, J.-Ch.
Cherubini, S.
and
Pastur, L.
2018.
Successive bifurcations in a fully three-dimensional open cavity flow.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
855.
Liu, Qiong
Sun, Yiyang
Cattafesta, Louis N.
Ukeiley, Lawrence S.
and
Taira, Kunihiko
2018.
Resolvent Analysis of Compressible Flow over a Long Rectangular Cavity.
Liu, Qiong
and
Gómez, Francisco
2018.
On the role of trailing edge geometry in cavity flow control.
Yeh, Chi-An
and
Taira, Kunihiko
2019.
Resolvent-analysis-based design of airfoil separation control.
Journal of Fluid Mechanics,
Vol. 867,
Issue. ,
p.
572.
Liu, Q.
and
Gómez, F.
2019.
Role of Trailing-Edge Geometry in Open Cavity Flow Control.
AIAA Journal,
Vol. 57,
Issue. 2,
p.
876.
Taira, Kunihiko
Hemati, Maziar S.
Brunton, Steven L.
Sun, Yiyang
Duraisamy, Karthik
Bagheri, Shervin
Dawson, Scott T. M.
and
Yeh, Chi-An
2020.
Modal Analysis of Fluid Flows: Applications and Outlook.
AIAA Journal,
Vol. 58,
Issue. 3,
p.
998.
Sun, Yiyang
Liu, Qiong
Cattafesta III, Louis N.
Ukeiley, Lawrence S.
and
Taira, Kunihiko
2020.
Resolvent Analysis of Compressible Laminar and Turbulent Cavity Flows.
AIAA Journal,
Vol. 58,
Issue. 3,
p.
1046.
Liu, Qiong
and
Gaitonde, Datta
2021.
Acoustic response of turbulent cavity flow using resolvent analysis.
Physics of Fluids,
Vol. 33,
Issue. 5,
Liu, Qiong
Sun, Yiyang
Yeh, Chi-An
Ukeiley, Lawrence S.
Cattafesta, Louis N.
and
Taira, Kunihiko
2021.
Unsteady control of supersonic turbulent cavity flow based on resolvent analysis.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Mathias, Marlon Sproesser
and
de Medeiros, Marcello Augusto Faraco
2022.
Optimal computational parameters for maximum accuracy and minimum cost of Arnoldi-based time-stepping methods for flow global stability analysis.
Theoretical and Computational Fluid Dynamics,
Vol. 36,
Issue. 6,
p.
1013.
Liu, Qiong
Prasad, Chitrarth
and
Gaitonde, Datta V.
2022.
Resolvent Analysis of an Under-expanded Planar Supersonic Impinging Jet.
Callaham, Jared L.
Brunton, Steven L.
and
Loiseau, Jean-Christophe
2022.
On the role of nonlinear correlations in reduced-order modelling.
Journal of Fluid Mechanics,
Vol. 938,
Issue. ,
Liu, Qiong
Gaitonde, Datta V.
and
Ranjan, Rajesh
2022.
Global Stability Analysis of Flow Behind an Upswept Aftbody.
AIAA Journal,
Vol. 60,
Issue. 2,
p.
1257.
Kant, Ravi
Acharya, Samarth
and
Bhoraniya, Ramesh
2024.
Fluid Mechanics and Fluid Power, Volume 2.
p.
313.
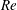 $Re$ incompressible flow over a long rectangular finite-span open cavity
$Re$ incompressible flow over a long rectangular finite-span open cavity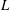 $L$ :
$L$ : 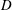 $D$ :
$D$ : 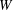 $W$
$W$ $=$ 6 : 1 : 2 to unsteadiness. The steady laminar three-dimensional flow loses stability at
$=$ 6 : 1 : 2 to unsteadiness. The steady laminar three-dimensional flow loses stability at 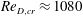 $\mathit{Re}_{D,cr}\approx 1080$ as a consequence of linear amplification of a travelling eigenmode that is qualitatively analogous to the shear-layer mode known from analyses of flow in spanwise-periodic cavities, but has a three-dimensional structure which is strongly influenced by the cavity lateral walls. Differences in the eigenspectrum of the present and the spanwise homogeneous flow configuration are documented. Topological changes exerted on the steady laminar flow by linear amplification of the unstable shear-layer mode are reminiscent of observations in experiments at an order of magnitude higher Reynolds number.
$\mathit{Re}_{D,cr}\approx 1080$ as a consequence of linear amplification of a travelling eigenmode that is qualitatively analogous to the shear-layer mode known from analyses of flow in spanwise-periodic cavities, but has a three-dimensional structure which is strongly influenced by the cavity lateral walls. Differences in the eigenspectrum of the present and the spanwise homogeneous flow configuration are documented. Topological changes exerted on the steady laminar flow by linear amplification of the unstable shear-layer mode are reminiscent of observations in experiments at an order of magnitude higher Reynolds number.


