Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-04T19:48:01.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent Taylor–Couette flow with stationary inner cylinder

Published online by Cambridge University Press:  21 June 2016

R. Ostilla-Mónico ,
R. Verzicco  and
D. Lohse
R. Ostilla-Mónico*
Affiliation:
Physics of Fluids Group, Mesa$+$ Institute and J.M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands School of Engineering and Applied Sciences and Kavli Institute for Bionano Science and Technology, Harvard University, Cambridge, MA 02138, USA
R. Verzicco
Affiliation:
Physics of Fluids Group, Mesa$+$ Institute and J.M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Dipartimento di Ingegneria Industriale, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Roma 00133, Italy
D. Lohse
Affiliation:
Physics of Fluids Group, Mesa$+$ Institute and J.M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A series of direct numerical simulations were performed of Taylor–Couette (TC) flow, the flow between two coaxial cylinders, with the outer cylinder rotating and the inner one fixed. Three cases were considered, where the Reynolds number of the outer cylinder was 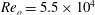$Re_{o}=5.5\times 10^{4}$, 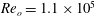$Re_{o}=1.1\times 10^{5}$ and 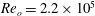$Re_{o}=2.2\times 10^{5}$. The ratio of radii 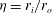${\it\eta}=r_{i}/r_{o}$ was fixed to 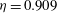${\it\eta}=0.909$ to mitigate the effects of curvature. Axially periodic boundary conditions were used, with the aspect ratio of vertical periodicity 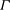${\it\Gamma}$ fixed to 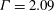${\it\Gamma}=2.09$. Being linearly stable, TC flow with outer cylinder rotation is known to have very different behaviour than TC flow with pure inner cylinder rotation. Here, we find that the flow nonetheless becomes turbulent, but the torque required to drive the cylinders and level of velocity fluctuations was found to be smaller than those for pure inner cylinder rotation at comparable Reynolds numbers. The mean angular momentum profiles showed a large gradient in the bulk, instead of the constant angular momentum profiles of pure inner cylinder rotation. The near-wall mean and fluctuation velocity profiles were found to coincide only very close to the wall, showing large deviations from both pure inner cylinder rotation profiles and the classic von Karman law of the wall elsewhere. Finally, transport of angular velocity was found to occur mainly through intermittent bursts, and not through wall-attached large-scale structures as is the case for pure inner cylinder rotation.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent convection
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 799 , 25 July 2016 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andereck, C. D., Dickman, R. & Swinney, H. L. 1983 New flows in a circular Couette system with corotating cylinders. Phys. Fluids 26, 1395–1401.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
van Atta, C. W. 1966 Exploratory measurements in spiral turbulence. J. Fluid Mech. 25 (3), 495–512.Google Scholar
Avsarkisov, V., Hoyas, S., Oberlack, M. & García-Galache, J. P. 2014 Turbulent plane Couette flow at moderately high Reynolds number. J. Fluid Mech. 751, R1–8.CrossRefGoogle Scholar
Borrero-Echeverry, D.2014 Sub-critical transition to turbulence in Taylor–Couette flow. PhD thesis, Georgia Institute of Technology, Atlanta, GA.Google Scholar
Borrero-Echeverry, D., Schatz, M. F. & Tagg, R. 2010 Transient turbulence in Taylor–Couette flow. Phys. Rev. E 81, 025301.Google Scholar
Brauckmann, H., Salewski, M. & Eckhardt, B. 2016 Momentum transport in Taylor–Couette flow with vanishing curvature. J. Fluid Mech. 790, 419–452.Google Scholar
Brauckmann, H. J. & Eckhardt, B. 2013 Intermittent boundary layers and torque maxima in Taylor–Couette flow. Phys. Rev. E 87 (3), 033004.Google Scholar
Burin, M. J. & Czarnocki, C. J. 2012 Subcritical transition and spiral turbulence in circular Couette flow. J. Fluid Mech. 709, 106–122.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.Google Scholar
Deguchi, K., Meseguer, A. & Mellibovsky, F. 2014 Subcritical equilibria in Taylor–Couette flow. Phys. Rev. Lett. 112, 184502.CrossRefGoogle ScholarPubMed
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P. Y., Richard, D. & Zahn, J. P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17, 095103.Google Scholar
Eckhardt, B., Faisst, H., Schmiegel, A. & Schneider, T. 2008 Dynamical systems and the transition to turbulence in linearly stable shear flows. Phil. Trans. R. Soc. Lond. A 366, 1297–1315.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Fardin, M. A., Perge, C. & Taberlet, N. 2014 The hydrogen atom of fluid dynamics – introduction to the Taylor–Couette flow for soft matter scientists. Soft Matt. 10 (20), 3523–3535.Google Scholar
van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118–149.Google Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High-Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.Google Scholar
Huisman, S. G., van der Veen, R. C. A., Sun, C. & Lohse, D. 2014 Multiple states in highly turbulent Taylor–Couette flow. Nat. Commun. 5, 3820.Google Scholar
Jimenez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid. Mech. 44, 27–45.CrossRefGoogle Scholar
Nordsiek, F., Huisman, S. G., van der Veen, R. C. A., Sun, C., Lohse, D. & Lathrop, D. P. 2015 Azimuthal velocity profiles in Rayleigh-stable Taylor–Couette flow and implied axial angular momentum transport. J. Fluid Mech. 774, 342–362.Google Scholar
Ostilla-Monico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014a Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
Ostilla-Monico, R., Verzicco, R., Grossmann, S. & Lohse, D. 2014b Turbulence decay towards the linearly-stable regime of Taylor–Couette flow. J. Fluid Mech. 747, 1–29.Google Scholar
Ostilla-Mónico, R., Verzicco, R., Grossmann, S. & Lohse, D. 2016 The near-wall region of highly turbulent Taylor–Couette flow. J. Fluid Mech. 768, 95–117.Google Scholar
Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2015 Effects of the computational domain size on DNS of Taylor–Couette turbulence with stationary outer cylinder. Phys. Fluids 27, 025110.Google Scholar
Paoletti, M. S., van Gils, D. P. M., Dubrulle, B., Sun, C., Lohse, D. & Lathrop, D. P. 2012 Angular momentum transport and turbulence in laboratory models of Keplerian flows. Astron. Astrophys. 547, A64.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2014 Turbulence statistics in Couette flow at high Reynolds number. J. Fluid Mech. 758, 327–343.Google Scholar
van der Poel, E. P., Ostilla-Monico, R., Donners, J. & Verzicco, R. 2015 A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids 116, 10–16.Google Scholar
Rayleigh, Lord 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–157.Google Scholar
Romanov, V. A. 1973 Stability of plane-parallel Couette flow. Funct. Anal. Applics. 7 (2), 137–146.Google Scholar
Taylor, G. I. 1923 Experiments on the motion of solid bodies in rotating fluids. Proc. R. Soc. Lond. A 104, 213–218.Google Scholar
Taylor, G. I. 1936 Fluid friction between rotating cylinders. Proc. R. Soc. Lond. A 157, 546–564.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flow in cylindrical coordinates. J. Comput. Phys. 123, 402–413.Google Scholar