The dynamics of two slender Hopf-linked vortex rings at vortex Reynolds numbers (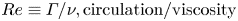 $Re \equiv \varGamma /\nu, \mathrm {circulation/viscosity}$)
$Re \equiv \varGamma /\nu, \mathrm {circulation/viscosity}$) 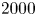 $2000$,
$2000$, 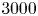 $3000$ and
$3000$ and 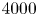 $4000$ is studied using direct numerical simulations of the incompressible Navier–Stokes equations. Under self-induction, the initially perpendicularly placed vortex rings approach each other and reconnect to form two separate vortex rings. The leading ring is closely cuddled and further undergoes secondary reconnection to form two even smaller rings. At high
$4000$ is studied using direct numerical simulations of the incompressible Navier–Stokes equations. Under self-induction, the initially perpendicularly placed vortex rings approach each other and reconnect to form two separate vortex rings. The leading ring is closely cuddled and further undergoes secondary reconnection to form two even smaller rings. At high 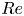 $Re$, the leading ring and the subsequent smaller rings are unstable and break up into turbulent clouds consisting of numerous even smaller-scale structures. Although the global helicity
$Re$, the leading ring and the subsequent smaller rings are unstable and break up into turbulent clouds consisting of numerous even smaller-scale structures. Although the global helicity 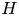 $H$ remains constant before reconnection, it increases and then rapidly decays during reconnection – both the growth and decay rates increase with
$H$ remains constant before reconnection, it increases and then rapidly decays during reconnection – both the growth and decay rates increase with 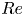 $Re$. In the two higher
$Re$. In the two higher 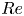 $Re$ (i.e. 3000 and 4000) cases,
$Re$ (i.e. 3000 and 4000) cases, 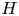 $H$ further rises after the first reconnection and reaches a quasi-plateau with the asymptotic value continuously increasing with
$H$ further rises after the first reconnection and reaches a quasi-plateau with the asymptotic value continuously increasing with 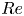 $Re$ – suggesting that
$Re$ – suggesting that 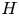 $H$ for viscous flows is not conserved at very high
$H$ for viscous flows is not conserved at very high 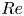 $Re$. Further flow analysis demonstrates that significant numbers of positive and negative helical structures are simultaneously generated before and during reconnection, and their different decay rates is the main reason for the complex evolution of
$Re$. Further flow analysis demonstrates that significant numbers of positive and negative helical structures are simultaneously generated before and during reconnection, and their different decay rates is the main reason for the complex evolution of 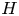 $H$. By examining the topological aspects of the helicity dynamics, we find that, different from
$H$. By examining the topological aspects of the helicity dynamics, we find that, different from 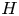 $H$, the sum of link and writhe (
$H$, the sum of link and writhe (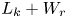 $L_k+W_r$) continuously drop during reconnection. Our results also clearly demonstrate that the twist, which increases with
$L_k+W_r$) continuously drop during reconnection. Our results also clearly demonstrate that the twist, which increases with 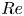 $Re$, plays a significant role in the helicity dynamics, particularly at high
$Re$, plays a significant role in the helicity dynamics, particularly at high 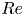 $Re$.
$Re$.