We demonstrate that gravity acting alone at large length scales (compared to the capillary length) can produce a jet from a sufficiently steep, axisymmetric surface deformation imposed on a quiescent, deep pool of liquid. Mechanistically, the jet owes it origin to the focusing of a concentric, surface wave towards the axis of symmetry, quite analogous to such focusing of capillary waves and resultant jet formation observed during bubble collapse at small scales. A weakly nonlinear theory based on the method of multiple scales in the potential flow limit is presented for a modal (single-mode) initial condition representing the solution to the primary Cauchy–Poisson problem. A pair of novel, coupled, amplitude equations are derived governing the modulation of the primary mode. For moderate values of the perturbation parameter 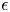 $\epsilon$ (a measure of the initial perturbation steepness), our second-order theory captures the overshoot (incipient jet) at the axis of symmetry quite well, demonstrating good agreement with numerical simulation of the incompressible, Euler equation with gravity (Popinet 2014, Basilisk. http://basilisk.fr) and no surface tension. We demonstrate that the underlying wave focusing mechanism may be understood in terms of radially inward motion of nodal points of a linearised, axisymmetric, standing wave. This explanation rationalises the ubiquitous observation of such jets accompanying cavity collapse phenomena, spanning length scales from microns to several metres. Expectedly, our theory becomes inaccurate as
$\epsilon$ (a measure of the initial perturbation steepness), our second-order theory captures the overshoot (incipient jet) at the axis of symmetry quite well, demonstrating good agreement with numerical simulation of the incompressible, Euler equation with gravity (Popinet 2014, Basilisk. http://basilisk.fr) and no surface tension. We demonstrate that the underlying wave focusing mechanism may be understood in terms of radially inward motion of nodal points of a linearised, axisymmetric, standing wave. This explanation rationalises the ubiquitous observation of such jets accompanying cavity collapse phenomena, spanning length scales from microns to several metres. Expectedly, our theory becomes inaccurate as 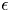 $\epsilon$ approaches unity. In this strongly nonlinear regime, slender jets form with surface accelerations exceeding gravity by more than an order of magnitude. In this inertial regime, we compare the jets in our simulations with the inertial, self-similar, analytical solution by Longuet-Higgins (J. Fluid Mech., 1983, vol. 127, pp. 103–121) and find qualitative agreement with the same. This analysis demonstrates, from first principles, an example of a jet created purely under gravity from a smooth initial perturbation and provides support to the analytical model of Longuet-Higgins (J. Fluid Mech., 1983, vol. 127, pp. 103–121).
$\epsilon$ approaches unity. In this strongly nonlinear regime, slender jets form with surface accelerations exceeding gravity by more than an order of magnitude. In this inertial regime, we compare the jets in our simulations with the inertial, self-similar, analytical solution by Longuet-Higgins (J. Fluid Mech., 1983, vol. 127, pp. 103–121) and find qualitative agreement with the same. This analysis demonstrates, from first principles, an example of a jet created purely under gravity from a smooth initial perturbation and provides support to the analytical model of Longuet-Higgins (J. Fluid Mech., 1983, vol. 127, pp. 103–121).