A direct numerical simulation investigation of a transient flow in a channel with a smooth top wall and a roughened bottom wall made of close-packed pyramids is presented. An initially stationary turbulent flow is accelerated rapidly to a new flow rate and the transient flow behaviour after the acceleration is studied. The equivalent roughness heights of the initial and final flows are 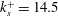 $k_{s}^{+}=14.5$ and 41.5, respectively. Immediately after the acceleration ends, the induced change behaves in a ‘plug-flow’ manner. Above the roughness crests, the additional velocity due to the perturbation flow is uniform; below the crest, it reduces approximately linearly to zero at the bottom of the roughness elements. The interaction of the perturbation flow with the rough wall is characterised by a series of events that resemble those observed in roughness-induced laminar–turbulent transitions. The process has two broad stages. In the first of these, large-scale vortices, comparable in extent to the roughness wavelength, develop around each roughness element and high-speed streaks form along the ridge lines of the elements. After a short time, each vortex splits into two, namely (i) a standing vortex in front of the element and (ii) a counter-rotating hairpin vortex behind it. The former is largely inactive, but the latter advects downstream with increasing strength, and later lifts away from the wall. These hairpin vortices wrap around strong low-speed streaks. The second stage of the overall process is the breakdown of the hairpin vortices into many smaller multi-scale vortices distributed randomly in space, leading eventually to a state of conventional turbulence. Shortly after the beginning of the first stage, the three components of the r.m.s of the velocity fluctuation all increase significantly in the near-wall region as a result of the vortical structures, and their spectra bear strong signatures of the surface topology. During the second stage, the overall turbulence energy in this region varies only slightly, but the spectrum evolves significantly, eventually approaching that of conventional turbulence. The direct effect of roughness on the flow is confined to a region up to approximately three element heights above the roughness crests. Turbulence in the core region does not begin to increase until after the transition near the wall is largely complete. The processes of transition over the smooth and rough walls of the channel are practically independent of each other. The flow over the smooth wall follows a laminar–turbulent transition and, as known from previous work, resembles a free-stream turbulence-induced boundary layer bypass transition.
$k_{s}^{+}=14.5$ and 41.5, respectively. Immediately after the acceleration ends, the induced change behaves in a ‘plug-flow’ manner. Above the roughness crests, the additional velocity due to the perturbation flow is uniform; below the crest, it reduces approximately linearly to zero at the bottom of the roughness elements. The interaction of the perturbation flow with the rough wall is characterised by a series of events that resemble those observed in roughness-induced laminar–turbulent transitions. The process has two broad stages. In the first of these, large-scale vortices, comparable in extent to the roughness wavelength, develop around each roughness element and high-speed streaks form along the ridge lines of the elements. After a short time, each vortex splits into two, namely (i) a standing vortex in front of the element and (ii) a counter-rotating hairpin vortex behind it. The former is largely inactive, but the latter advects downstream with increasing strength, and later lifts away from the wall. These hairpin vortices wrap around strong low-speed streaks. The second stage of the overall process is the breakdown of the hairpin vortices into many smaller multi-scale vortices distributed randomly in space, leading eventually to a state of conventional turbulence. Shortly after the beginning of the first stage, the three components of the r.m.s of the velocity fluctuation all increase significantly in the near-wall region as a result of the vortical structures, and their spectra bear strong signatures of the surface topology. During the second stage, the overall turbulence energy in this region varies only slightly, but the spectrum evolves significantly, eventually approaching that of conventional turbulence. The direct effect of roughness on the flow is confined to a region up to approximately three element heights above the roughness crests. Turbulence in the core region does not begin to increase until after the transition near the wall is largely complete. The processes of transition over the smooth and rough walls of the channel are practically independent of each other. The flow over the smooth wall follows a laminar–turbulent transition and, as known from previous work, resembles a free-stream turbulence-induced boundary layer bypass transition.
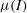 ${\it\mu}(I)$-rheology for dense granular avalanches
${\it\mu}(I)$-rheology for dense granular avalanches
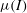 ${\it\mu}(I)$-rheology for granular flow
${\it\mu}(I)$-rheology for granular flow