1. Introduction
Seagrasses exhibit a rich set of dynamical behaviours due to their collective interaction with fluid flows. The hydrodynamic processes resulting from this behaviour influence many environmental processes such as sedimentation, transport of dissolved oxygen, plant growth and biomass production (Fonseca & Kenworthy Reference Fonseca and Kenworthy1987; Grizzle et al. Reference Grizzle, Short, Newell, Hoven and Kindblom1996; Nepf Reference Nepf1999, Reference Nepf2012). One response of the submerged grass beds to steady currents is the formation of coherent large-amplitude oscillations, known as monami (Ackerman & Okubo Reference Ackerman and Okubo1993). In this article, we present a linear hydrodynamic instability underlying the onset of these coherent oscillations.
Current explanations of monami (Ikeda & Kanazawa Reference Ikeda and Kanazawa1996; Raupach, Finnigan & Brunet Reference Raupach, Finnigan and Brunet1996; Ghisalberti & Nepf Reference Ghisalberti and Nepf2002) invoke the existence of a shear layer at the top of the grass bed (henceforth called grass top) due to vegetation drag. Its instability, through a mechanism similar to the Kelvin–Helmholtz (KH) instability, is thought to lead to coherent eddies over the grass bed. The grass responds to these eddies by deforming, which leads to large-amplitude synchronous oscillations of the grass blades. This picture can be used to derive a simple scaling dependence of the monami frequency on the flow speed and the shear layer thickness, and to understand transport in the seagrass bed (Nepf & Vivoni Reference Nepf and Vivoni2000; Ghisalberti & Nepf Reference Ghisalberti and Nepf2002, Reference Ghisalberti and Nepf2004; Okamoto, Nezu & Ikeda Reference Okamoto, Nezu and Ikeda2012).
However, several aspects of this explanation remain unsatisfactory. The instability is modelled using the inviscid Rayleigh equation, and despite the role of drag in producing the shear layer, its role in damping the perturbations is ignored (Raupach et al. Reference Raupach, Finnigan and Brunet1996). Furthermore, the shear layer is assumed not to be influenced by the top and bottom boundaries of the domain, although the experimentally measured thickness of the shear layer is, in many cases, comparable to the unvegetated water depth. The velocity profile of the free shear layer is assumed ad hoc to be piecewise linear (Py, De Langre & Moulia Reference Py, De Langre and Moulia2006) or hyperbolic tangent (Raupach et al. Reference Raupach, Finnigan and Brunet1996; Ghisalberti & Nepf Reference Ghisalberti and Nepf2002), with parameters fitted using the experimental observations. The origin of these profiles, the values of the fitted parameters, and their effect on monami remain unexplained. Finally, no existing theory explains the threshold flow speed, observed in the laboratory (Ghisalberti & Nepf Reference Ghisalberti and Nepf2002) and in the field (Grizzle et al. Reference Grizzle, Short, Newell, Hoven and Kindblom1996), below which monami is not observed.
Here, we present a mathematical model for the linear instability that accounts for these effects. Although monami is manifested in the motion of the grass, the drag exerted by the vegetation on the flow is central to the hypothesized instability. The instability and the resulting flow structures persist in laboratory experiments even when flexible grass mimics are replaced by rigid dowels (Ghisalberti & Nepf Reference Ghisalberti and Nepf2002, Reference Ghisalberti and Nepf2006). Therefore, to develop the essential mathematical model, we assume the grass blades to be rigid and oriented vertically (along the
![]() $y$
direction) on average. The vegetation is modelled as a continuum drag on the fluid acting perpendicular to the blade orientation and proportional to the grass density. In the limit of dense vegetation, the steady profile established in the presence of the drag exhibits a localized region of enhanced shear gradient near the grass top and drives a flow instability. While some features of the instability are similar to KH instability, we also find significant differences. This comparison is the focus of this article.
$y$
direction) on average. The vegetation is modelled as a continuum drag on the fluid acting perpendicular to the blade orientation and proportional to the grass density. In the limit of dense vegetation, the steady profile established in the presence of the drag exhibits a localized region of enhanced shear gradient near the grass top and drives a flow instability. While some features of the instability are similar to KH instability, we also find significant differences. This comparison is the focus of this article.
2. Mathematical model
The vegetation is assumed to be sufficiently dense so that the drag exerted by it may be modelled by a continuous body force
![]() $\boldsymbol{f}$
entering the equation governing the flow as
$\boldsymbol{f}$
entering the equation governing the flow as
where
![]() ${\it\rho}$
,
${\it\rho}$
,
![]() $\boldsymbol{u}=(u,v)$
and
$\boldsymbol{u}=(u,v)$
and
![]() $p$
are the fluid density, velocity, and the dynamic pressure respectively, and
$p$
are the fluid density, velocity, and the dynamic pressure respectively, and
![]() ${\it\mu}$
is the (dynamic) eddy viscosity. The Reynolds number of the flow based on the scale of the grass blade is
${\it\mu}$
is the (dynamic) eddy viscosity. The Reynolds number of the flow based on the scale of the grass blade is
![]() $O(10^{2}{-}10^{3})$
; therefore, neglecting skin friction, we model the form drag on the vegetation as
$O(10^{2}{-}10^{3})$
; therefore, neglecting skin friction, we model the form drag on the vegetation as
![]() $\boldsymbol{f}=-N_{g}C_{N}{\it\rho}u|u|d\hat{\boldsymbol{x}}$
(Nepf Reference Nepf1999; Nepf & Vivoni Reference Nepf and Vivoni2000; Ghisalberti & Nepf Reference Ghisalberti and Nepf2004), where
$\boldsymbol{f}=-N_{g}C_{N}{\it\rho}u|u|d\hat{\boldsymbol{x}}$
(Nepf Reference Nepf1999; Nepf & Vivoni Reference Nepf and Vivoni2000; Ghisalberti & Nepf Reference Ghisalberti and Nepf2004), where
![]() $N_{g}$
is the number of grass blades per unit horizontal area,
$N_{g}$
is the number of grass blades per unit horizontal area,
![]() $C_{N}$
is the drag coefficient for the flow normal to the grass,
$C_{N}$
is the drag coefficient for the flow normal to the grass,
![]() $\hat{\boldsymbol{x}}$
is the unit vector in the horizontal direction and
$\hat{\boldsymbol{x}}$
is the unit vector in the horizontal direction and
![]() $d$
is the average blade width projected perpendicular to the flow. In the interest of simplicity, we model the turbulence using an eddy viscosity; see § 5.3 for a detailed discussion. In the field,
$d$
is the average blade width projected perpendicular to the flow. In the interest of simplicity, we model the turbulence using an eddy viscosity; see § 5.3 for a detailed discussion. In the field,
![]() $C_{N}$
,
$C_{N}$
,
![]() $N_{g}$
and
$N_{g}$
and
![]() ${\it\mu}$
vary with position, but we do not expect these variations to be central to the instability mechanism, and therefore take them to be constants.
${\it\mu}$
vary with position, but we do not expect these variations to be central to the instability mechanism, and therefore take them to be constants.
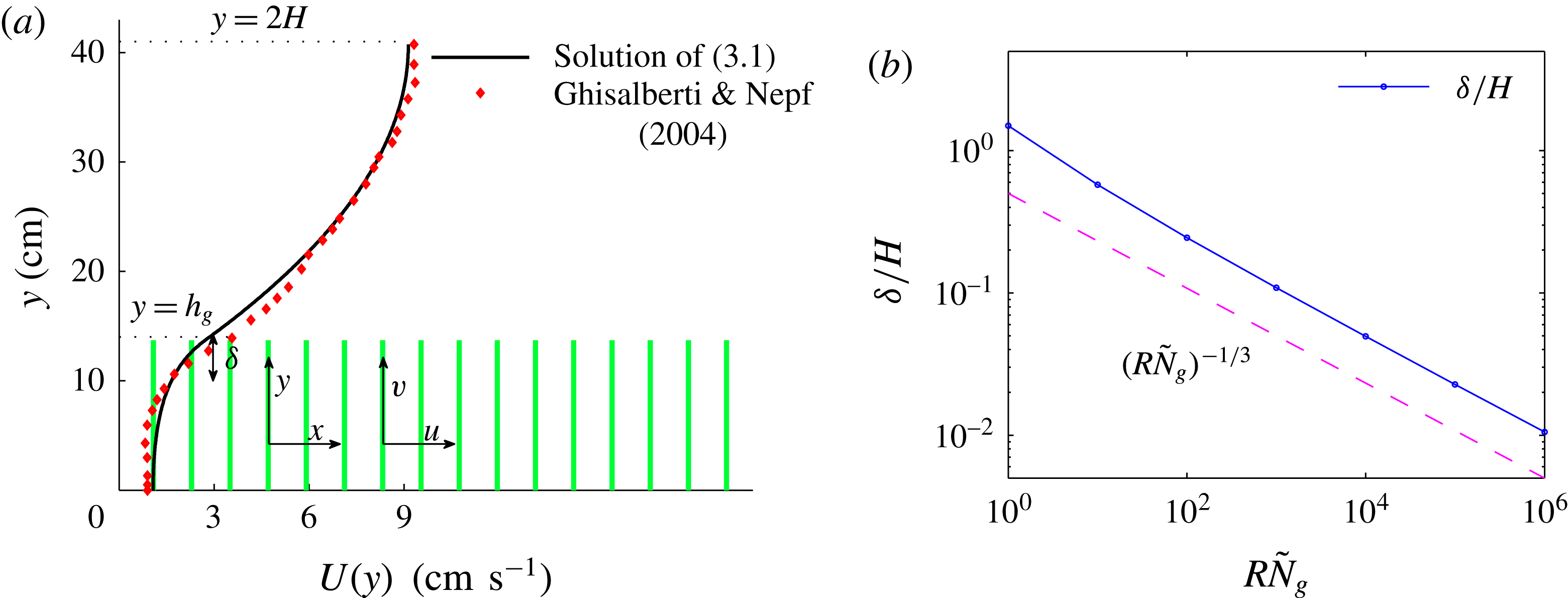
Figure 1. (a) Schematic set-up and comparison of our steady flow profile with that from the experiments in Ghisalberti & Nepf (Reference Ghisalberti and Nepf2004) (case I from table 1) and its approximation with
![]() $U_{0}=7.28$
cm s
$U_{0}=7.28$
cm s
![]() $^{-1}$
and
$^{-1}$
and
![]() ${\it\delta}=5.02$
cm in our model. The grass extends up to
${\it\delta}=5.02$
cm in our model. The grass extends up to
![]() $y=h_{g}$
in the water column of depth
$y=h_{g}$
in the water column of depth
![]() $2H$
. The steady velocity profile can be decomposed into a parabolic profile in the unvegetated region, a uniform profile deep within the vegetation and a boundary layer of thickness
$2H$
. The steady velocity profile can be decomposed into a parabolic profile in the unvegetated region, a uniform profile deep within the vegetation and a boundary layer of thickness
![]() ${\it\delta}$
near the grass top. (b) The dependence of the boundary layer thickness (estimated as
${\it\delta}$
near the grass top. (b) The dependence of the boundary layer thickness (estimated as
![]() $|U/U_{y}|$
at
$|U/U_{y}|$
at
![]() $y=h_{g}$
from the numerical solution of (3.1)) on the vegetation density parameter
$y=h_{g}$
from the numerical solution of (3.1)) on the vegetation density parameter
![]() $R{\tilde{N}}_{g}$
.
$R{\tilde{N}}_{g}$
.
3. Linear stability analysis
We first calculate the fully developed steady solution
![]() $\boldsymbol{u}=U(y)\hat{\boldsymbol{x}}$
of (2.1) driven by a constant pressure gradient
$\boldsymbol{u}=U(y)\hat{\boldsymbol{x}}$
of (2.1) driven by a constant pressure gradient
![]() $\text{d}P/\text{d}x$
in a water column of depth
$\text{d}P/\text{d}x$
in a water column of depth
![]() $2H$
and vegetated depth
$2H$
and vegetated depth
![]() $h_{g}$
, and use it to non-dimensionalize the mathematical model. The momentum balance (2.1) for
$h_{g}$
, and use it to non-dimensionalize the mathematical model. The momentum balance (2.1) for
![]() $U(y)$
simplifies to
$U(y)$
simplifies to
where
![]() $S(y)=1$
for
$S(y)=1$
for
![]() $0<y<h_{g}$
and
$0<y<h_{g}$
and
![]() $S(y)=0$
for
$S(y)=0$
for
![]() $h_{g}<y<2H$
. Equation (3.1) is solved subject to no shear at the boundaries, i.e.
$h_{g}<y<2H$
. Equation (3.1) is solved subject to no shear at the boundaries, i.e.
![]() $U^{\prime }(0)=U^{\prime }(2H)=0$
. The lower boundary condition is appropriate for dense vegetation because the shear stress exerted by the bottom surface is expected to be negligible compared with the vegetation drag (Nepf & Vivoni Reference Nepf and Vivoni2000), whereas the upper boundary condition models the free interface. A comparison of the steady flow profile from the solution of (3.1) with experimental measurements by Ghisalberti & Nepf (Reference Ghisalberti and Nepf2004) is shown in figure 1. The profile
$U^{\prime }(0)=U^{\prime }(2H)=0$
. The lower boundary condition is appropriate for dense vegetation because the shear stress exerted by the bottom surface is expected to be negligible compared with the vegetation drag (Nepf & Vivoni Reference Nepf and Vivoni2000), whereas the upper boundary condition models the free interface. A comparison of the steady flow profile from the solution of (3.1) with experimental measurements by Ghisalberti & Nepf (Reference Ghisalberti and Nepf2004) is shown in figure 1. The profile
![]() $U(y)$
has three distinct regions, as determined by a matched asymptotic analysis (Hinch Reference Hinch1991). Within the vegetation, it is approximately uniform with
$U(y)$
has three distinct regions, as determined by a matched asymptotic analysis (Hinch Reference Hinch1991). Within the vegetation, it is approximately uniform with
![]() $U(y)\approx U_{g}=\sqrt{(-\text{d}P/\text{d}x)/({\it\rho}C_{N}dN_{g})}$
, arising from a balance of the drag with the pressure gradient. Outside the vegetation, the velocity has a simple parabolic profile. At the grass top, continuity of shear stresses results in a boundary layer of thickness
$U(y)\approx U_{g}=\sqrt{(-\text{d}P/\text{d}x)/({\it\rho}C_{N}dN_{g})}$
, arising from a balance of the drag with the pressure gradient. Outside the vegetation, the velocity has a simple parabolic profile. At the grass top, continuity of shear stresses results in a boundary layer of thickness
![]() ${\it\delta}$
. Denoting
${\it\delta}$
. Denoting
![]() $U_{bl}$
to be the velocity scale in the boundary layer and
$U_{bl}$
to be the velocity scale in the boundary layer and
![]() $U_{0}=(-\text{d}P/\text{d}x)\,H^{2}/{\it\mu}$
to be the velocity scale in the unvegetated region, the balance between viscous forces and vegetation drag implies
$U_{0}=(-\text{d}P/\text{d}x)\,H^{2}/{\it\mu}$
to be the velocity scale in the unvegetated region, the balance between viscous forces and vegetation drag implies
![]() ${\it\mu}U_{bl}/{\it\delta}^{2}\sim {\it\rho}C_{N}dN_{g}U_{bl}^{2}$
, and the continuity of shear stress across the grass top implies
${\it\mu}U_{bl}/{\it\delta}^{2}\sim {\it\rho}C_{N}dN_{g}U_{bl}^{2}$
, and the continuity of shear stress across the grass top implies
![]() $U_{bl}/{\it\delta}\sim U_{0}/H$
. Solving for
$U_{bl}/{\it\delta}\sim U_{0}/H$
. Solving for
![]() ${\it\delta}$
and
${\it\delta}$
and
![]() $U_{bl}$
yields
$U_{bl}$
yields
![]() ${\it\delta}/H\sim U_{bl}/U_{0}\sim (R{\tilde{N}}_{g})^{-1/3}$
, where
${\it\delta}/H\sim U_{bl}/U_{0}\sim (R{\tilde{N}}_{g})^{-1/3}$
, where
![]() ${\tilde{N}}_{g}=(C_{N}dHN_{g})$
is the vegetation frontal area per bed area and
${\tilde{N}}_{g}=(C_{N}dHN_{g})$
is the vegetation frontal area per bed area and
![]() $R={\it\rho}U_{0}H/{\it\mu}$
is the Reynolds number of the flow. A numerical estimate of
$R={\it\rho}U_{0}H/{\it\mu}$
is the Reynolds number of the flow. A numerical estimate of
![]() ${\it\delta}$
(estimated as
${\it\delta}$
(estimated as
![]() $U/U_{y}$
at
$U/U_{y}$
at
![]() $y=h_{g}$
) is compared with this prediction in figure 1 (inset). We identify the boundary layer to be analogous to the shear layer invoked by Ghisalberti & Nepf (Reference Ghisalberti and Nepf2002, Reference Ghisalberti and Nepf2004) in the previous explanation of monami. This dependence of
$y=h_{g}$
) is compared with this prediction in figure 1 (inset). We identify the boundary layer to be analogous to the shear layer invoked by Ghisalberti & Nepf (Reference Ghisalberti and Nepf2002, Reference Ghisalberti and Nepf2004) in the previous explanation of monami. This dependence of
![]() ${\it\delta}$
on
${\it\delta}$
on
![]() $N_{g}$
gives us a way to systematically investigate the effect of the shear layer thickness on the instability mechanism. Figure 1 also shows that the asymptotic regime of a thin boundary layer is expected to hold for
$N_{g}$
gives us a way to systematically investigate the effect of the shear layer thickness on the instability mechanism. Figure 1 also shows that the asymptotic regime of a thin boundary layer is expected to hold for
![]() $R{\tilde{N}}_{g}\gtrsim 100$
. In this notation,
$R{\tilde{N}}_{g}\gtrsim 100$
. In this notation,
![]() $U_{g}/U_{0}=(R{\tilde{N}}_{g})^{-1/2}$
(used later in deriving (5.3)).
$U_{g}/U_{0}=(R{\tilde{N}}_{g})^{-1/2}$
(used later in deriving (5.3)).
Next, we substitute
![]() $\boldsymbol{u}=(U+\tilde{u} ,\tilde{v})$
,
$\boldsymbol{u}=(U+\tilde{u} ,\tilde{v})$
,
![]() $p=P+\tilde{p}$
in (2.1) and expand to linear order to investigate the evolution of small perturbations
$p=P+\tilde{p}$
in (2.1) and expand to linear order to investigate the evolution of small perturbations
![]() $(\tilde{u} ,\tilde{v})$
, which obey
$(\tilde{u} ,\tilde{v})$
, which obey
where the tildes are dropped. These equations are non-dimensionalized using the half-channel height
![]() $H$
, velocity
$H$
, velocity
![]() $U_{0}$
and time
$U_{0}$
and time
![]() $H/U_{0}$
, leading to three non-dimensional parameters, namely
$H/U_{0}$
, leading to three non-dimensional parameters, namely
![]() $R$
,
$R$
,
![]() ${\tilde{N}}_{g}$
and the vegetation submergence ratio
${\tilde{N}}_{g}$
and the vegetation submergence ratio
![]() $h_{g}/H$
. We also use
$h_{g}/H$
. We also use
![]() ${\it\delta}/H$
in lieu of
${\it\delta}/H$
in lieu of
![]() ${\tilde{N}}_{g}$
to parametrize the vegetation density and help to elucidate the instability mechanism. Using a stream function
${\tilde{N}}_{g}$
to parametrize the vegetation density and help to elucidate the instability mechanism. Using a stream function
![]() ${\it\psi}$
with
${\it\psi}$
with
![]() $u={\it\psi}_{y},v=-{\it\psi}_{x}$
to satisfy mass balance, we seek a solution of the form
$u={\it\psi}_{y},v=-{\it\psi}_{x}$
to satisfy mass balance, we seek a solution of the form
![]() $(u,v,{\it\psi})=(\hat{u} (y),\hat{v}(y),{\it\phi}(y))\text{e}^{\text{i}kx+{\it\sigma}t}$
to obtain a modified Orr–Sommerfeld equation (Drazin & Reid Reference Drazin and Reid1981; Chu, Wu & Khayat Reference Chu, Wu and Khayat1991; Chen & Jirka Reference Chen and Jirka1997),
$(u,v,{\it\psi})=(\hat{u} (y),\hat{v}(y),{\it\phi}(y))\text{e}^{\text{i}kx+{\it\sigma}t}$
to obtain a modified Orr–Sommerfeld equation (Drazin & Reid Reference Drazin and Reid1981; Chu, Wu & Khayat Reference Chu, Wu and Khayat1991; Chen & Jirka Reference Chen and Jirka1997),
where
![]() $D=\text{d}/\text{d}y$
, and subject to the boundary conditions
$D=\text{d}/\text{d}y$
, and subject to the boundary conditions
![]() ${\it\phi}=D^{2}{\it\phi}=0$
at
${\it\phi}=D^{2}{\it\phi}=0$
at
![]() $y=0$
and
$y=0$
and
![]() $y=2$
. The growth rate
$y=2$
. The growth rate
![]() ${\it\sigma}$
for a given wavenumber
${\it\sigma}$
for a given wavenumber
![]() $k$
appears as an eigenvalue that allows a non-trivial solution
$k$
appears as an eigenvalue that allows a non-trivial solution
![]() ${\it\phi}$
of (3.4). We solve (3.4) numerically for
${\it\phi}$
of (3.4). We solve (3.4) numerically for
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() ${\it\phi}$
.
${\it\phi}$
.
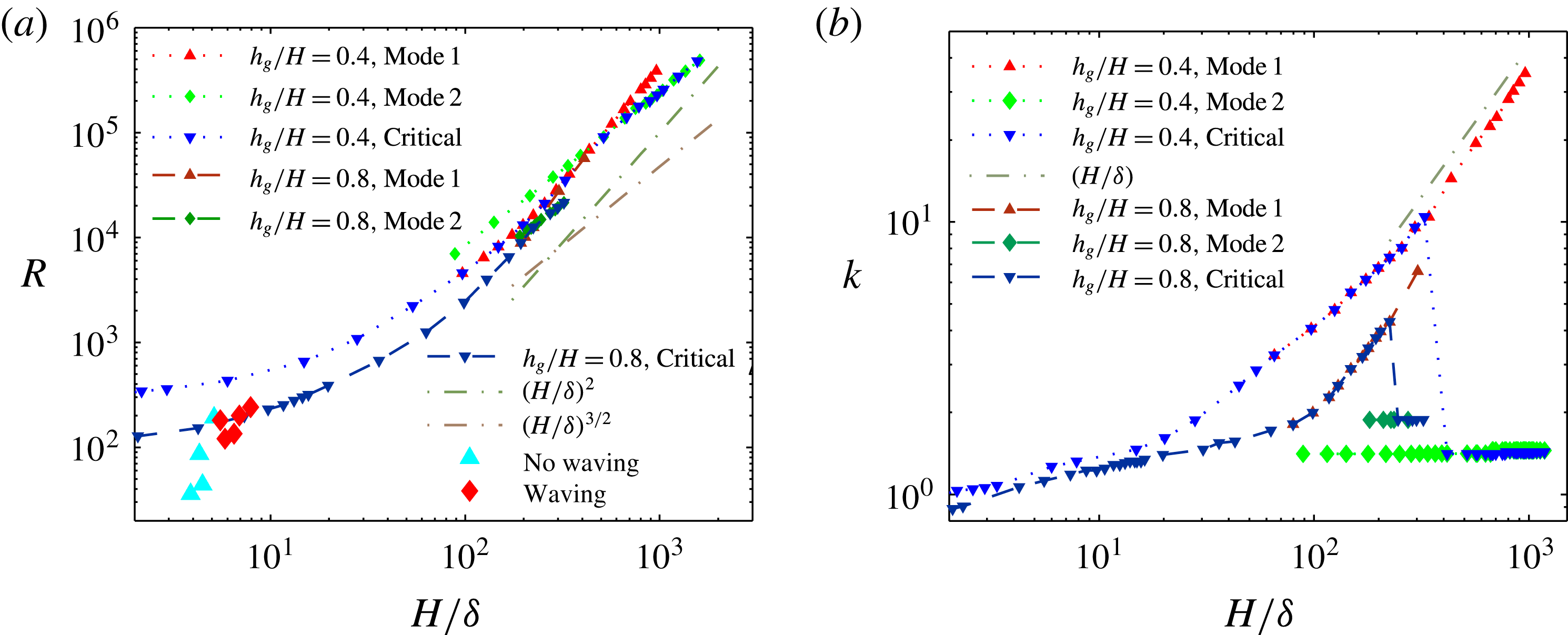
Figure 2. Critical Reynolds number, threshold Reynolds number for modes 1 and 2 (a) and the corresponding marginally stable wavenumber (b) for different submergence ratios as a function of vegetation density parametrized by the boundary layer thickness. Parameters from experiments reported by Ghisalberti & Nepf (Reference Ghisalberti and Nepf2002) to exhibit or suppress synchronous waving are also included in (b).
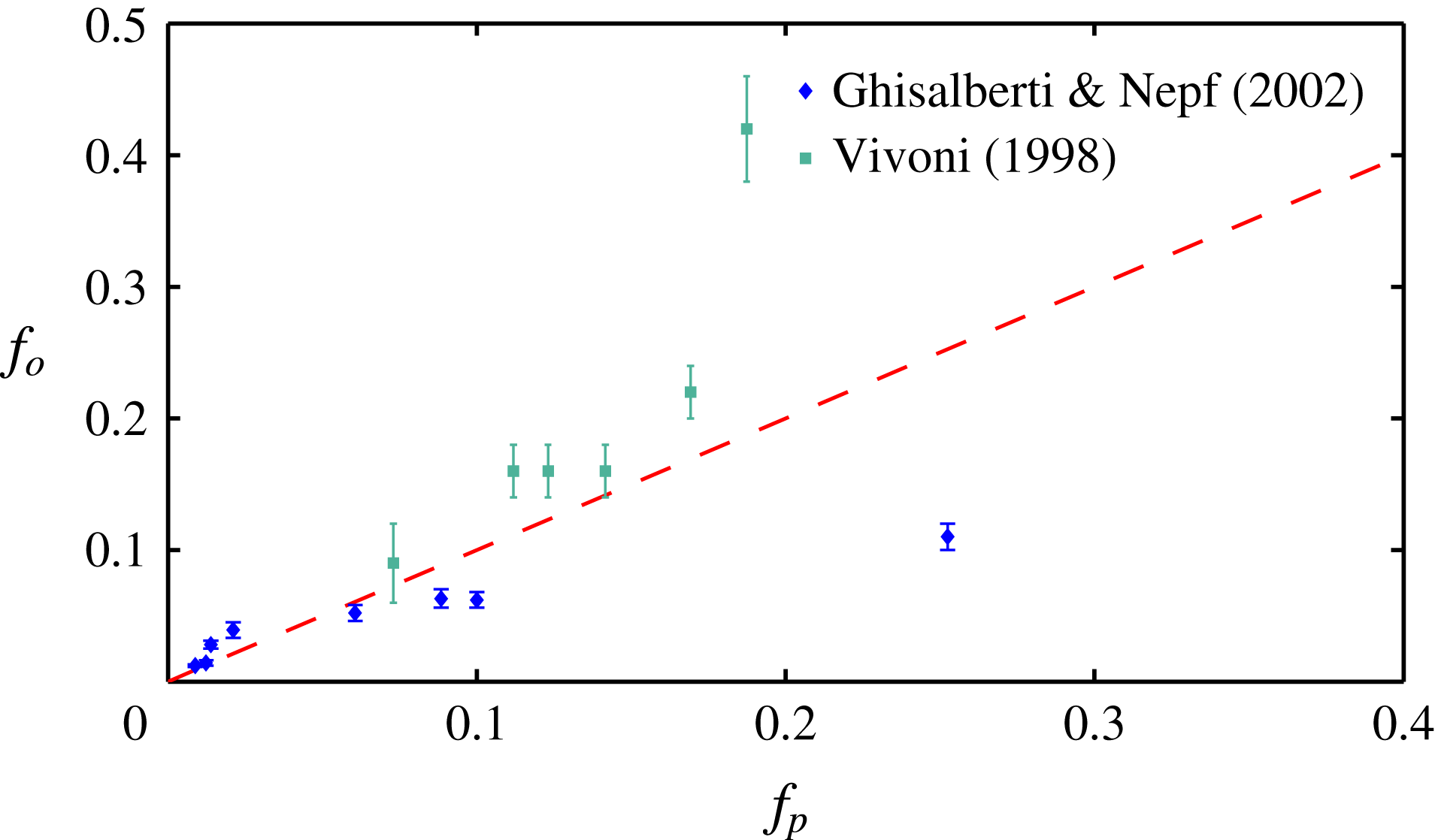
Figure 3. Comparison of the experimentally measured dominant frequency
![]() $f_{o}$
(in Hz) with the predictions
$f_{o}$
(in Hz) with the predictions
![]() $f_{p}=\text{Im}({\it\sigma})$
from the solution of (3.4). The experimental data are obtained from Ghisalberti & Nepf (Reference Ghisalberti and Nepf2002) and Vivoni (Reference Vivoni1998).
$f_{p}=\text{Im}({\it\sigma})$
from the solution of (3.4). The experimental data are obtained from Ghisalberti & Nepf (Reference Ghisalberti and Nepf2002) and Vivoni (Reference Vivoni1998).
4. Results – unstable modes and critical parameters
A threshold in
![]() $R$
, above which the flow is unstable (
$R$
, above which the flow is unstable (
![]() $\text{Re}({\it\sigma})>0$
) for at least one
$\text{Re}({\it\sigma})>0$
) for at least one
![]() $k$
, emerges from the solution of (3.4). The dependence of this threshold
$k$
, emerges from the solution of (3.4). The dependence of this threshold
![]() $R$
, and the corresponding marginally stable wavenumber
$R$
, and the corresponding marginally stable wavenumber
![]() $k$
, on
$k$
, on
![]() ${\it\delta}/H$
and
${\it\delta}/H$
and
![]() $h_{g}/H$
is shown in figure 2, and is found to compare well with experimental observations of Ghisalberti & Nepf (Reference Ghisalberti and Nepf2002). The threshold
$h_{g}/H$
is shown in figure 2, and is found to compare well with experimental observations of Ghisalberti & Nepf (Reference Ghisalberti and Nepf2002). The threshold
![]() $R$
increases with the vegetation density, indicating a competition between the destabilizing shear in the flow and the stabilizing effect of damping due to vegetation drag. The frequency (
$R$
increases with the vegetation density, indicating a competition between the destabilizing shear in the flow and the stabilizing effect of damping due to vegetation drag. The frequency (
![]() $\text{Im}({\it\sigma})$
) of the fastest growing mode also agrees well with the observed behaviour – frequency of monami, maxima in the velocity spectra and frequency of vortex passage in laboratory scale experiments (Ghisalberti & Nepf Reference Ghisalberti and Nepf2002) – for cases where the vegetation was sufficiently dense to be modelled by a continuum drag field, as shown in figure 3. The measured values of the eddy viscosity vary with depth in the water column (Ghisalberti & Nepf Reference Ghisalberti and Nepf2004); we use
$\text{Im}({\it\sigma})$
) of the fastest growing mode also agrees well with the observed behaviour – frequency of monami, maxima in the velocity spectra and frequency of vortex passage in laboratory scale experiments (Ghisalberti & Nepf Reference Ghisalberti and Nepf2002) – for cases where the vegetation was sufficiently dense to be modelled by a continuum drag field, as shown in figure 3. The measured values of the eddy viscosity vary with depth in the water column (Ghisalberti & Nepf Reference Ghisalberti and Nepf2004); we use
![]() ${\it\mu}=0.1$
Pa s as a representative value from this range for comparison with experiments. Figure 2 also shows that the predicted dimensionless wavenumber of the dominant mode for parameters corresponding to the laboratory scale experiments (
${\it\mu}=0.1$
Pa s as a representative value from this range for comparison with experiments. Figure 2 also shows that the predicted dimensionless wavenumber of the dominant mode for parameters corresponding to the laboratory scale experiments (
![]() $4<H/{\it\delta}<10$
) is very close to unity, and therefore the dimensional wavelength is approximately
$4<H/{\it\delta}<10$
) is very close to unity, and therefore the dimensional wavelength is approximately
![]() $2{\rm\pi}H$
.
$2{\rm\pi}H$
.
To better understand the instability mechanism, we consider the dependence of the fastest growing wavenumber on
![]() ${\it\delta}$
. The fastest growing wavenumber first increases proportional to
${\it\delta}$
. The fastest growing wavenumber first increases proportional to
![]() $H/{\it\delta}$
, but at a critical
$H/{\it\delta}$
, but at a critical
![]() ${\it\delta}$
discontinuously jumps and remains
${\it\delta}$
discontinuously jumps and remains
![]() $O(1)$
(see figure 2). To aid in explaining this behaviour, we show heat maps of
$O(1)$
(see figure 2). To aid in explaining this behaviour, we show heat maps of
![]() $\text{Re}({\it\sigma})$
as a function of
$\text{Re}({\it\sigma})$
as a function of
![]() $R$
and
$R$
and
![]() $k$
for different values of
$k$
for different values of
![]() $h_{g}/H$
and
$h_{g}/H$
and
![]() ${\tilde{N}}_{g}$
in figure 4. The smallest
${\tilde{N}}_{g}$
in figure 4. The smallest
![]() $R$
on the neutral curve (
$R$
on the neutral curve (
![]() $\text{Re}({\it\sigma})=0$
) sets the threshold. We observe that as
$\text{Re}({\it\sigma})=0$
) sets the threshold. We observe that as
![]() ${\tilde{N}}_{g}$
increases, the unstable region splits into two; we refer to the region with the higher
${\tilde{N}}_{g}$
increases, the unstable region splits into two; we refer to the region with the higher
![]() $k$
as ‘mode 1’ and the one with the lower
$k$
as ‘mode 1’ and the one with the lower
![]() $k$
as ‘mode 2’. For
$k$
as ‘mode 2’. For
![]() $h_{g}/H\lesssim 0.9$
, the unstable region for mode 1 recedes to higher
$h_{g}/H\lesssim 0.9$
, the unstable region for mode 1 recedes to higher
![]() $R$
, and for
$R$
, and for
![]() $h_{g}/H\gtrsim 0.9$
, the region shrinks to zero size. In either case, due to such behaviour the most unstable mode transitions discontinuously from mode 1 to mode 2. All experimental data we have found correspond to a vegetation density for which the unstable region in the
$h_{g}/H\gtrsim 0.9$
, the region shrinks to zero size. In either case, due to such behaviour the most unstable mode transitions discontinuously from mode 1 to mode 2. All experimental data we have found correspond to a vegetation density for which the unstable region in the
![]() $R{-}k$
space has not split into two, so we are unable to determine whether the flow instability in the laboratory scale experiments (Ghisalberti & Nepf Reference Ghisalberti and Nepf2002) is due to mode 1 or mode 2.
$R{-}k$
space has not split into two, so we are unable to determine whether the flow instability in the laboratory scale experiments (Ghisalberti & Nepf Reference Ghisalberti and Nepf2002) is due to mode 1 or mode 2.
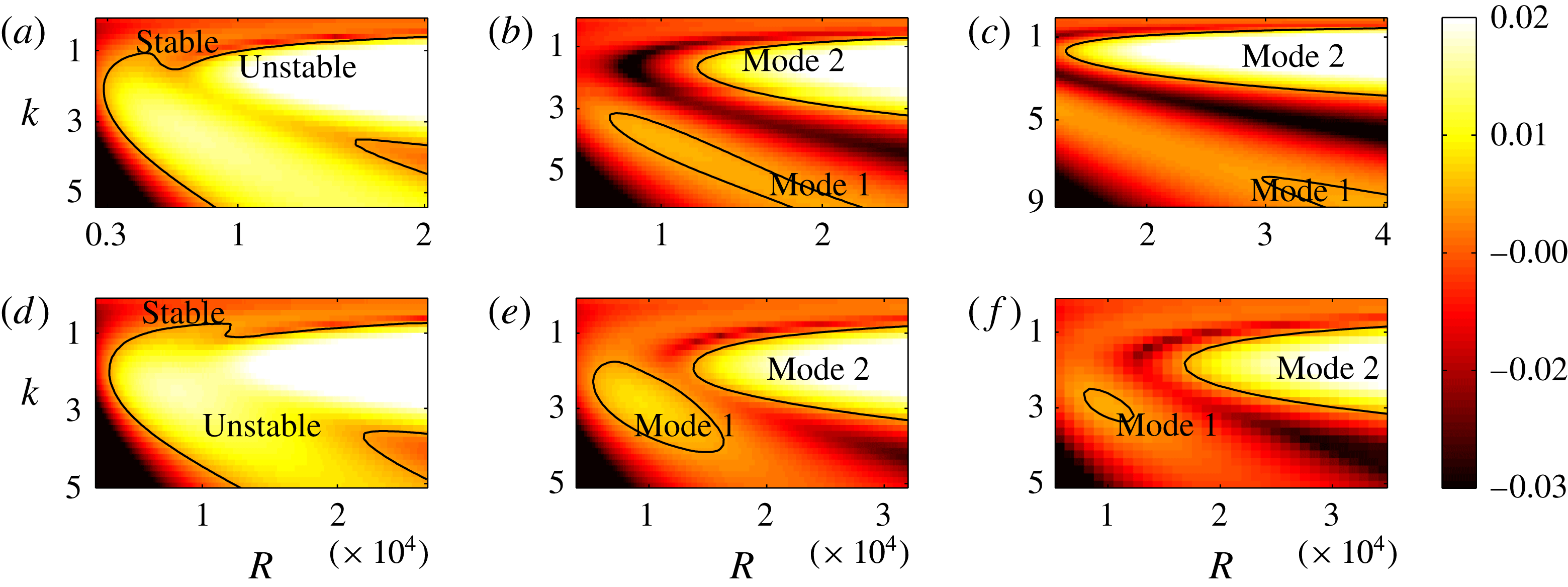
Figure 4. Heat maps of
![]() $\text{Re}({\it\sigma})$
and the neutral curve (
$\text{Re}({\it\sigma})$
and the neutral curve (
![]() $\text{Re}({\it\sigma})=0$
) as a function of wavenumber and
$\text{Re}({\it\sigma})=0$
) as a function of wavenumber and
![]() $R$
for (a)
$R$
for (a)
![]() $h_{g}/H=0.8$
,
$h_{g}/H=0.8$
,
![]() ${\tilde{N}}_{g}=500$
; (b)
${\tilde{N}}_{g}=500$
; (b)
![]() $h_{g}/H=0.8$
,
$h_{g}/H=0.8$
,
![]() ${\tilde{N}}_{g}=850$
; (c)
${\tilde{N}}_{g}=850$
; (c)
![]() $h_{g}/H=0.8$
,
$h_{g}/H=0.8$
,
![]() ${\tilde{N}}_{g}=925$
; (d)
${\tilde{N}}_{g}=925$
; (d)
![]() $h_{g}/H=1$
,
$h_{g}/H=1$
,
![]() ${\tilde{N}}_{g}=900$
; (e)
${\tilde{N}}_{g}=900$
; (e)
![]() $h_{g}/H=1$
,
$h_{g}/H=1$
,
![]() ${\tilde{N}}_{g}=1400$
; (f)
${\tilde{N}}_{g}=1400$
; (f)
![]() $h_{g}/H=1$
,
$h_{g}/H=1$
,
![]() ${\tilde{N}}_{g}=1700$
. As
${\tilde{N}}_{g}=1700$
. As
![]() ${\tilde{N}}_{g}$
increases, the unstable region splits into two regions labelled as ‘mode 1’ and ‘mode 2’. For
${\tilde{N}}_{g}$
increases, the unstable region splits into two regions labelled as ‘mode 1’ and ‘mode 2’. For
![]() ${\tilde{N}}_{g}$
below (above) a critical value, mode 1 (mode 2) sets the threshold
${\tilde{N}}_{g}$
below (above) a critical value, mode 1 (mode 2) sets the threshold
![]() $R$
.
$R$
.
5. Discussion – comparison of unstable modes with the KH instability mechanism
The distinct asymptotic behaviour of the two modes as
![]() ${\tilde{N}}_{g}\gg 1$
distinguishes them from each other and facilitate comparison with the KH instability mechanism.
${\tilde{N}}_{g}\gg 1$
distinguishes them from each other and facilitate comparison with the KH instability mechanism.
5.1. Mode 1
We numerically observe that the threshold Reynolds number for mode 1 instability scales as
![]() $R\sim (H/{\it\delta})^{2}$
(or
$R\sim (H/{\it\delta})^{2}$
(or
![]() $R\propto {{\tilde{N}}_{g}}^{2}$
). Our calculations also show that mode 1 asymptotically localizes to the boundary layer near the grass top, and exhibits highest growth for a perturbation of
$R\propto {{\tilde{N}}_{g}}^{2}$
). Our calculations also show that mode 1 asymptotically localizes to the boundary layer near the grass top, and exhibits highest growth for a perturbation of
![]() $k\sim H/{\it\delta}$
(see figure 2). The behaviour of this critical Reynolds number can be understood by considering the limit
$k\sim H/{\it\delta}$
(see figure 2). The behaviour of this critical Reynolds number can be understood by considering the limit
![]() $R\gg 1$
and
$R\gg 1$
and
![]() ${\tilde{N}}_{g}\gg 1$
. Estimating the size of various terms of (3.4) within the boundary layer in this limit helps us to understand the behaviour of the critical
${\tilde{N}}_{g}\gg 1$
. Estimating the size of various terms of (3.4) within the boundary layer in this limit helps us to understand the behaviour of the critical
![]() $R$
. Using
$R$
. Using
![]() $D\sim H/{\it\delta}$
,
$D\sim H/{\it\delta}$
,
![]() ${\it\sigma}\sim O(1)$
and
${\it\sigma}\sim O(1)$
and
![]() $U=U_{bl}\sim {\it\delta}/H$
in the boundary layer, the magnitude of the advection term is
$U=U_{bl}\sim {\it\delta}/H$
in the boundary layer, the magnitude of the advection term is
![]() $(H/{\it\delta})^{2}$
(or
$(H/{\it\delta})^{2}$
(or
![]() $R^{2/3}{\tilde{N}}_{g}^{2/3}$
), and the viscous and vegetation drag terms are
$R^{2/3}{\tilde{N}}_{g}^{2/3}$
), and the viscous and vegetation drag terms are
![]() $(1/R)({\it\delta}/H)^{-4}$
(or
$(1/R)({\it\delta}/H)^{-4}$
(or
![]() $(R^{1/3}{\tilde{N}}_{g})^{4/3}$
). The advection term, viscous term and vegetation drag terms balance when
$(R^{1/3}{\tilde{N}}_{g})^{4/3}$
). The advection term, viscous term and vegetation drag terms balance when
![]() $R\sim (H/{\it\delta})^{2}$
(or
$R\sim (H/{\it\delta})^{2}$
(or
![]() $R\sim {{\tilde{N}}_{g}}^{2}$
).
$R\sim {{\tilde{N}}_{g}}^{2}$
).
To further understand the mechanism of mode 1, we rescale (3.4) near the grass top using the boundary layer scalings
![]() ${\it\eta}=y/({\it\delta}/H)$
,
${\it\eta}=y/({\it\delta}/H)$
,
![]() $U(y)=({\it\delta}/H)\bar{U}({\it\eta})$
and
$U(y)=({\it\delta}/H)\bar{U}({\it\eta})$
and
![]() $k=(H/{\it\delta})\bar{k}$
. With these scalings (3.4) simplifies to
$k=(H/{\it\delta})\bar{k}$
. With these scalings (3.4) simplifies to
in a region of thickness
![]() $O({\it\delta})$
near
$O({\it\delta})$
near
![]() $y=h_{g}$
, where
$y=h_{g}$
, where
![]() $\bar{D}=\text{d}/\text{d}{\it\eta}$
. Since
$\bar{D}=\text{d}/\text{d}{\it\eta}$
. Since
![]() $(R/{\tilde{N}}_{g}^{2})$
is the only remaining parameter in (5.1), the mode shape and solution are expected to converge in the limit
$(R/{\tilde{N}}_{g}^{2})$
is the only remaining parameter in (5.1), the mode shape and solution are expected to converge in the limit
![]() $R\gg 1$
,
$R\gg 1$
,
![]() ${\tilde{N}}_{g}\gg 1$
, but
${\tilde{N}}_{g}\gg 1$
, but
![]() $R/{\tilde{N}}_{g}^{2}$
fixed. Our numerical findings confirm this expectation; the critical
$R/{\tilde{N}}_{g}^{2}$
fixed. Our numerical findings confirm this expectation; the critical
![]() $R$
scales as
$R$
scales as
![]() $(H/{\it\delta})^{2}$
, as shown in figure 2, and the mode shapes are self-similar with length scale
$(H/{\it\delta})^{2}$
, as shown in figure 2, and the mode shapes are self-similar with length scale
![]() ${\it\delta}$
, as shown in figure 5.
${\it\delta}$
, as shown in figure 5.
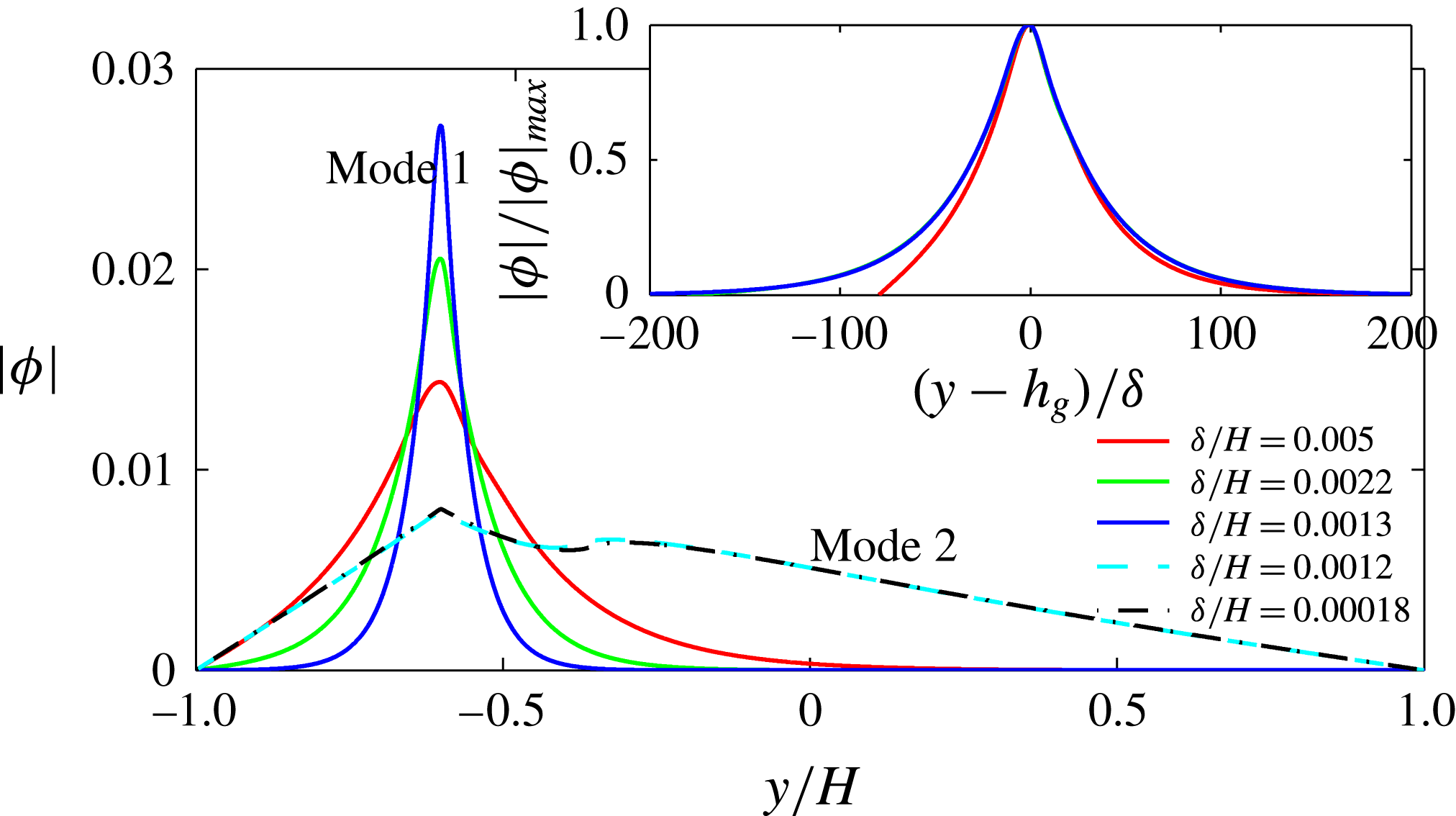
Figure 5. Plot of the neutral mode 1 (solid) and mode 2 (dashed) shapes
![]() $|{\it\phi}|$
in the limit of small
$|{\it\phi}|$
in the limit of small
![]() ${\it\delta}/H$
for
${\it\delta}/H$
for
![]() $h_{g}/H=0.2$
. The approach of the mode shapes to each other for these small values of
$h_{g}/H=0.2$
. The approach of the mode shapes to each other for these small values of
![]() ${\it\delta}/H$
indicates that the dense vegetation asymptote is reached. Mode 1 shapes appear to be self-similar in shape as
${\it\delta}/H$
indicates that the dense vegetation asymptote is reached. Mode 1 shapes appear to be self-similar in shape as
![]() ${\it\delta}\rightarrow 0$
. The inset shows that the rescaled
${\it\delta}\rightarrow 0$
. The inset shows that the rescaled
![]() $|{\it\phi}|$
for mode 1 as a function of
$|{\it\phi}|$
for mode 1 as a function of
![]() $(y-h_{g})/{\it\delta}$
approaches a universal shape, indicating that an asymptotic limit has been reached.
$(y-h_{g})/{\it\delta}$
approaches a universal shape, indicating that an asymptotic limit has been reached.
Table 1. Comparison between the KH instability and the two unstable modes resulting from solution of (3.4).

Mode 1 shares many characteristics with the KH instability (see table 1). The fastest growing wavenumber at the critical
![]() $R$
scales as
$R$
scales as
![]() $k\propto (H/{\it\delta})$
, similarly to the KH instability. The extent of the unstable mode is also localized to the boundary layer region. The porous nature of the vegetation implies that a weak flow of magnitude
$k\propto (H/{\it\delta})$
, similarly to the KH instability. The extent of the unstable mode is also localized to the boundary layer region. The porous nature of the vegetation implies that a weak flow of magnitude
![]() $U_{bl}=U_{0}{\it\delta}/H$
penetrates a thin boundary layer region
$U_{bl}=U_{0}{\it\delta}/H$
penetrates a thin boundary layer region
![]() ${\it\delta}$
, and therefore the shear gradient
${\it\delta}$
, and therefore the shear gradient
![]() $U_{yy}\sim U_{0}/{\it\delta}H$
is largest in this region. The strong shear gradient
$U_{yy}\sim U_{0}/{\it\delta}H$
is largest in this region. The strong shear gradient
![]() $U_{yy}$
in the boundary layer plays a central role in destabilizing the flow and localizing the instability to that region.
$U_{yy}$
in the boundary layer plays a central role in destabilizing the flow and localizing the instability to that region.
Our detailed description of mode 1, given by (5.1), also highlights key differences from formulations of the KH instability. The KH instability is usually described using the inviscid Rayleigh equation,
and is therefore not parametrized by the Reynolds number. Describing the instability using the Orr–Sommerfeld equation introduces the Reynolds number as a parameter, but shear flows with tanh profiles are unstable for all values of the parameter (Drazin & Reid Reference Drazin and Reid1981). Therefore, based on inviscid formulations of the KH instability, the origin of the threshold flow conditions observed in experiments and in the field is unclear.
In our model, (turbulent eddy) viscosity sets the scale of the boundary layer, and therefore for mode 1. However, the boundary layer is established only in the vegetated region; the velocity profile does not saturate on the scale of
![]() ${\it\delta}$
in the unvegetated region. The threshold flow condition arises from a competition between the destabilizing role of fluid inertia, which is very similar to the role played in the KH instability, and the vegetation drag. The vegetation drag may not be neglected within this boundary layer, and therefore plays a central role in the mode 1 instability mechanism.
${\it\delta}$
in the unvegetated region. The threshold flow condition arises from a competition between the destabilizing role of fluid inertia, which is very similar to the role played in the KH instability, and the vegetation drag. The vegetation drag may not be neglected within this boundary layer, and therefore plays a central role in the mode 1 instability mechanism.
5.2. Mode 2
The threshold condition for mode 2 is numerically observed to be
![]() $R\propto ({\it\delta}/H)^{-3/2}$
(or
$R\propto ({\it\delta}/H)^{-3/2}$
(or
![]() $R\propto {\tilde{N}}_{g}$
) for
$R\propto {\tilde{N}}_{g}$
) for
![]() $k\sim O(1)$
, as shown in figure 2, which can be understood by assuming
$k\sim O(1)$
, as shown in figure 2, which can be understood by assuming
![]() $R\gg 1$
but fixed
$R\gg 1$
but fixed
![]() $R/{\tilde{N}}_{g}\sim O(1)$
. In this limit, the non-dimensional flow in the grass bed is
$R/{\tilde{N}}_{g}\sim O(1)$
. In this limit, the non-dimensional flow in the grass bed is
![]() $U_{g}/U_{0}\sim (R{\tilde{N}}_{g})^{-1/2}\ll 1$
, and therefore
$U_{g}/U_{0}\sim (R{\tilde{N}}_{g})^{-1/2}\ll 1$
, and therefore
![]() $\text{i}kU\ll {\it\sigma}$
may be neglected in comparison to
$\text{i}kU\ll {\it\sigma}$
may be neglected in comparison to
![]() ${\it\sigma}$
. Furthermore,
${\it\sigma}$
. Furthermore,
![]() $U_{yy}$
decays to zero within the grass outside the boundary layer. Outside the grass, the turbulent viscous stress term is negligible compared with the inertial term because
$U_{yy}$
decays to zero within the grass outside the boundary layer. Outside the grass, the turbulent viscous stress term is negligible compared with the inertial term because
![]() $R\gg 1$
. Thus, (3.4) simplifies to
$R\gg 1$
. Thus, (3.4) simplifies to
The structure of this mode in the aforementioned limit is such that
![]() ${\it\phi}$
is continuous at
${\it\phi}$
is continuous at
![]() $y=h_{g}$
, but
$y=h_{g}$
, but
![]() $D{\it\phi}$
undergoes a rapid transition there, on the scale of the boundary layer thickness
$D{\it\phi}$
undergoes a rapid transition there, on the scale of the boundary layer thickness
![]() ${\it\delta}$
. The eigenvalues and the mode shape are otherwise independent of
${\it\delta}$
. The eigenvalues and the mode shape are otherwise independent of
![]() ${\it\delta}$
. Therefore, we conclude that the boundary layer only plays a secondary role of regularizing the discontinuity in the tangential velocity at
${\it\delta}$
. Therefore, we conclude that the boundary layer only plays a secondary role of regularizing the discontinuity in the tangential velocity at
![]() $y=h_{g}$
. The enhanced shear in the boundary layer plays no role for this mode of instability.
$y=h_{g}$
. The enhanced shear in the boundary layer plays no role for this mode of instability.
Mode 2 has characteristics distinct from the KH instability. Outside the grass, the unstable mode shape is governed by the inviscid Rayleigh equation (5.2). An inflection point in
![]() $U(y)$
is a necessary condition for instability arising from (5.2) according to Rayleigh’s criteria (Rayleigh Reference Rayleigh1879). However, for our
$U(y)$
is a necessary condition for instability arising from (5.2) according to Rayleigh’s criteria (Rayleigh Reference Rayleigh1879). However, for our
![]() $U(y)$
profiles,
$U(y)$
profiles,
![]() $U_{yy}(y)=-1$
above the grass and therefore does not change sign for
$U_{yy}(y)=-1$
above the grass and therefore does not change sign for
![]() $y>h_{g}$
. Instead, the dynamics is coupled with the flow in the grass bed described by (5.3a
) in
$y>h_{g}$
. Instead, the dynamics is coupled with the flow in the grass bed described by (5.3a
) in
![]() $y<h_{g}$
. The absence of
$y<h_{g}$
. The absence of
![]() $U_{yy}$
in (5.3a
) indicates that
$U_{yy}$
in (5.3a
) indicates that
![]() $U_{yy}$
is approximated to be zero in
$U_{yy}$
is approximated to be zero in
![]() $y<h_{g}$
, and therefore the positive values of
$y<h_{g}$
, and therefore the positive values of
![]() $U_{yy}$
that occur in the boundary layer do not affect this mode of instability to leading order. Furthermore, the presence of the critical parameter
$U_{yy}$
that occur in the boundary layer do not affect this mode of instability to leading order. Furthermore, the presence of the critical parameter
![]() $R/{\tilde{N}}_{g}$
in (5.3a
) indicates the presence of alternative destabilizing dynamics, involving the interaction of flow in the unvegetated region governed by (5.2) with the flow in the vegetated region incorporating the drag. Therefore, we conclude that mode 2 is distinct from the KH instability and owes its existence to vegetation drag.
$R/{\tilde{N}}_{g}$
in (5.3a
) indicates the presence of alternative destabilizing dynamics, involving the interaction of flow in the unvegetated region governed by (5.2) with the flow in the vegetated region incorporating the drag. Therefore, we conclude that mode 2 is distinct from the KH instability and owes its existence to vegetation drag.
5.3. Role of the turbulence model
We have modelled the turbulence using a constant eddy viscosity. The simplicity of this model allows us to make progress and capture the essential features of the instability. However, this simplicity in some cases only provides a qualitatively accurate description of the flow. In this subsection, we present an account of the advantages and shortcomings of assuming a constant eddy viscosity to model the turbulence.
As a consequence of the constant eddy viscosity, the boundary layer thickness
![]() ${\it\delta}$
scales as
${\it\delta}$
scales as
![]() $H(R{\tilde{N}}_{g})^{-1/3}$
. Experimental observations show that the boundary layer thickness scales instead as
$H(R{\tilde{N}}_{g})^{-1/3}$
. Experimental observations show that the boundary layer thickness scales instead as
![]() ${\tilde{N}}_{g}^{-1}$
(Nepf, White & Murphy Reference Nepf, White and Murphy2007). While the precise boundary layer thickness is governed by the details of the turbulence model, the existence of this boundary layer for dense vegetation is independent of the turbulence model. We have captured one possible realization of this feature using a constant eddy viscosity. Experiments have also shown that a model based on a mixing length
${\tilde{N}}_{g}^{-1}$
(Nepf, White & Murphy Reference Nepf, White and Murphy2007). While the precise boundary layer thickness is governed by the details of the turbulence model, the existence of this boundary layer for dense vegetation is independent of the turbulence model. We have captured one possible realization of this feature using a constant eddy viscosity. Experiments have also shown that a model based on a mixing length
![]() $l$
better approximates the turbulent characteristics of the flow with
$l$
better approximates the turbulent characteristics of the flow with
![]() $l\sim {\it\delta}$
; i.e. the boundary layer itself establishes eddies to transport momentum. The eddy viscosity corresponding to this model is
$l\sim {\it\delta}$
; i.e. the boundary layer itself establishes eddies to transport momentum. The eddy viscosity corresponding to this model is
![]() ${\it\mu}\sim {\it\rho}U{\it\delta}$
, and the leading-order balance between turbulent momentum transport and vegetation drag is
${\it\mu}\sim {\it\rho}U{\it\delta}$
, and the leading-order balance between turbulent momentum transport and vegetation drag is
![]() ${\it\mu}U/{\it\delta}^{2}\sim {\it\rho}C_{N}dN_{g}U^{2}$
. Substituting
${\it\mu}U/{\it\delta}^{2}\sim {\it\rho}C_{N}dN_{g}U^{2}$
. Substituting
![]() ${\it\mu}$
yields
${\it\mu}$
yields
![]() ${\it\delta}/H\sim {\tilde{N}}_{g}^{-1}$
, in agreement with the experimental observations.
${\it\delta}/H\sim {\tilde{N}}_{g}^{-1}$
, in agreement with the experimental observations.
Within our framework, the mixing length model implies a scale for the eddy viscosity
![]() ${\it\mu}\sim {\it\rho}U_{bl}{\it\delta}$
at the grass top, which corresponds to an effective
${\it\mu}\sim {\it\rho}U_{bl}{\it\delta}$
at the grass top, which corresponds to an effective
![]() $R\sim U_{0}H/U_{bl}{\it\delta}$
. Furthermore, matching the slope of the velocity profile from the boundary layer to the unvegetated flow implies
$R\sim U_{0}H/U_{bl}{\it\delta}$
. Furthermore, matching the slope of the velocity profile from the boundary layer to the unvegetated flow implies
![]() $U_{bl}/U_{0}\sim {\it\delta}/H$
, and therefore
$U_{bl}/U_{0}\sim {\it\delta}/H$
, and therefore
![]() $R\sim (H/{\it\delta})^{2}$
. Substituting this relation in
$R\sim (H/{\it\delta})^{2}$
. Substituting this relation in
![]() ${\it\delta}/H\sim (R{\tilde{N}}_{g})^{-1/3}$
and solving for
${\it\delta}/H\sim (R{\tilde{N}}_{g})^{-1/3}$
and solving for
![]() ${\it\delta}$
yields
${\it\delta}$
yields
![]() ${\it\delta}/H\sim {\tilde{N}}_{g}^{-1}$
. This simple scaling analysis shows that the boundary layer thickness depends on the turbulence model, and indicates that turbulence models based on mixing lengths will yield more realistic scalings for the boundary layer thickness. At the same time, the qualitative features of the instability are represented by our analysis.
${\it\delta}/H\sim {\tilde{N}}_{g}^{-1}$
. This simple scaling analysis shows that the boundary layer thickness depends on the turbulence model, and indicates that turbulence models based on mixing lengths will yield more realistic scalings for the boundary layer thickness. At the same time, the qualitative features of the instability are represented by our analysis.
The mode 1 instability is driven by the intense shear on the scale of the boundary layer. The driving mechanism for this instability is similar to that of the KH instability, and relies only on the presence of this shear as presented in the
![]() $\bar{U}_{{\it\eta}{\it\eta}}$
term in (5.1). Therefore, we expect mode 1 instability to be exhibited independent of the turbulence model. We further expect the fastest growing wavenumber to be proportional to
$\bar{U}_{{\it\eta}{\it\eta}}$
term in (5.1). Therefore, we expect mode 1 instability to be exhibited independent of the turbulence model. We further expect the fastest growing wavenumber to be proportional to
![]() $1/{\it\delta}$
, and the mode to be localized to the boundary layer because these results have a basis in dimensional analysis. The threshold parameters for mode 1, however, may depend on the precise turbulence model used.
$1/{\it\delta}$
, and the mode to be localized to the boundary layer because these results have a basis in dimensional analysis. The threshold parameters for mode 1, however, may depend on the precise turbulence model used.
For the mode 2 instability, the turbulent momentum transport is found to be irrelevant to leading order. In the asymptotic limit of dense grass, (5.3) shows that the instability is driven by the interaction of the unvegetated flow with the vegetation drag. The influence of the turbulence model is limited to the regularization of the sharp transition in tangential velocity across the grass top. Therefore, we expect mode 2 and its features to be preserved even if a different turbulence model is used.
5.4. Comparison with previous models
A modified version of the Orr–Sommerfeld equation was analysed previously by Chu et al. (Reference Chu, Wu and Khayat1991), Chen & Jirka (Reference Chen and Jirka1997) and White & Nepf (Reference White and Nepf2007) in the context of instabilities in depth-averaged shallow water flows, where bottom friction replaces or augments vegetation drag. They assumed the steady profile to be a hyperbolic tangent, the drag to be isotropic and the flow domain to be infinite in
![]() $y$
. White & Nepf (Reference White and Nepf2007) also neglected the eddy viscosity in their stability analysis. While a detailed investigation needed to compare the consequences of the different assumptions is outside the scope of this paper, we discuss similarities and differences between their results and ours. These investigations only found one unstable mode. This is most likely so because the calculations were restricted to a parameter regime where the two modes had not separated from each other, as is the case shown in figure 4 for the lowest
$y$
. White & Nepf (Reference White and Nepf2007) also neglected the eddy viscosity in their stability analysis. While a detailed investigation needed to compare the consequences of the different assumptions is outside the scope of this paper, we discuss similarities and differences between their results and ours. These investigations only found one unstable mode. This is most likely so because the calculations were restricted to a parameter regime where the two modes had not separated from each other, as is the case shown in figure 4 for the lowest
![]() ${\tilde{N}}_{g}$
. These investigations also found that increasing the drag could further destabilize the flow, which is consistent with our interpretation of the mode 2 instability mechanism.
${\tilde{N}}_{g}$
. These investigations also found that increasing the drag could further destabilize the flow, which is consistent with our interpretation of the mode 2 instability mechanism.
The analogous oscillation of terrestrial canopies in wind, known as honami (Inoue Reference Inoue1956; Raupach et al.
Reference Raupach, Finnigan and Brunet1996), is different because the atmospheric boundary layer is much larger than the vegetation height. In the framework of our model, the limit of
![]() $h_{g}/H\ll 1$
while
$h_{g}/H\ll 1$
while
![]() ${\it\delta}/h_{g}=$
constant can be used to represent the hydrodynamic instability for the terrestrial case. We find that in this case, the transition from mode 1 to mode 2 occurs at such a large vegetation density that mode 2 is irrelevant. Hence, only the KH-like characteristics are observed in the terrestrial case.
${\it\delta}/h_{g}=$
constant can be used to represent the hydrodynamic instability for the terrestrial case. We find that in this case, the transition from mode 1 to mode 2 occurs at such a large vegetation density that mode 2 is irrelevant. Hence, only the KH-like characteristics are observed in the terrestrial case.
While predictions of the threshold
![]() $R$
for the onset of the instability and the frequency of oscillations are comparable to experimental observations, the deviation of our model predictions from the observations may be attributed to the various simplifications in our model. In real meadows, the grass is flexible, and the drag coefficient is known to vary from the bottom to the tip of the grass blades due to variation in vegetation characteristics (Vivoni Reference Vivoni1998; Nepf & Vivoni Reference Nepf and Vivoni2000). The turbulence model for the flow through the meadow can also be improved from one with constant eddy viscosity (Ghisalberti & Nepf Reference Ghisalberti and Nepf2002, Reference Ghisalberti and Nepf2004). Although these model improvements might lead to a better agreement between the observed and predicted quantities, the insight furnished by (5.1) and (5.3), and therefore our main conclusions, remain useful.
$R$
for the onset of the instability and the frequency of oscillations are comparable to experimental observations, the deviation of our model predictions from the observations may be attributed to the various simplifications in our model. In real meadows, the grass is flexible, and the drag coefficient is known to vary from the bottom to the tip of the grass blades due to variation in vegetation characteristics (Vivoni Reference Vivoni1998; Nepf & Vivoni Reference Nepf and Vivoni2000). The turbulence model for the flow through the meadow can also be improved from one with constant eddy viscosity (Ghisalberti & Nepf Reference Ghisalberti and Nepf2002, Reference Ghisalberti and Nepf2004). Although these model improvements might lead to a better agreement between the observed and predicted quantities, the insight furnished by (5.1) and (5.3), and therefore our main conclusions, remain useful.
We now test the assumption of an undeformable grass bed due to the dominant restoring force of buoyancy, using the criterion that the buoyancy time scale be much shorter than the hydrodynamic time scale
![]() $H/U_{0}$
. For a common seagrass, Zostera marina, the relative density difference is
$H/U_{0}$
. For a common seagrass, Zostera marina, the relative density difference is
![]() ${\rm\Delta}{\it\rho}/{\it\rho}\approx 0.25$
, the volume fraction is
${\rm\Delta}{\it\rho}/{\it\rho}\approx 0.25$
, the volume fraction is
![]() $V_{f}\approx 0.1$
and
$V_{f}\approx 0.1$
and
![]() $H=1$
m (Fonseca Reference Fonseca1998), yielding the buoyancy time scale to be
$H=1$
m (Fonseca Reference Fonseca1998), yielding the buoyancy time scale to be
![]() $\sqrt{{\it\rho}H/V_{f}{\rm\Delta}{\it\rho}g}\;\approx \;2$
s. The hydrodynamic time scale assuming
$\sqrt{{\it\rho}H/V_{f}{\rm\Delta}{\it\rho}g}\;\approx \;2$
s. The hydrodynamic time scale assuming
![]() $U_{0}\approx 0.1$
m s
$U_{0}\approx 0.1$
m s
![]() $^{-1}$
is 10 s, and is therefore longer than the buoyancy time scale. We have neither accounted for the pre-factors appearing in the scaling argument nor considered cases when the time scale separation is not so evident. Accounting for these factors can lead to further interesting behaviour (Py et al.
Reference Py, De Langre and Moulia2006; Gosselin & De Langre Reference Gosselin and De Langre2009), and motivates further investigation.
$^{-1}$
is 10 s, and is therefore longer than the buoyancy time scale. We have neither accounted for the pre-factors appearing in the scaling argument nor considered cases when the time scale separation is not so evident. Accounting for these factors can lead to further interesting behaviour (Py et al.
Reference Py, De Langre and Moulia2006; Gosselin & De Langre Reference Gosselin and De Langre2009), and motivates further investigation.
6. Conclusion
In conclusion, we have shown that the hydrodynamic instability underlying monami differs from the traditional KH instability due to the presence of the vegetation drag. The threshold flow condition observed in the field and in laboratory experiments arises due to the presence of this drag. Furthermore, our linear stability analysis reveals two modes, namely mode 1 with a mechanism similar to the KH instability and mode 2 with characteristics distinctly different from the KH instability. We are unable to determine based on observations, and therefore have refrained from identifying, which mode is observed in experiments. This still remains a subtle question and subject of future investigation. Since the two modes merge for the experimental parameters, the KH instability may not be assumed to underlie monami. The spatial structure of the instability modes has direct implications for transport in the grass bed. Our analysis also informs flow structure formation in many other related scenarios, such as flow over coral reefs and permeable sediments, and flow through urban environments. It is therefore expected to have a wider impact.
Acknowledgements
M.M.B. was supported by the Collective Interactions Unit, OIST Graduate University, while visiting Brown University. A.M. was supported by NSF 1131393. We thank H. Nepf, M. Ghisalberti, M. Luhar and L. Mahadevan for helpful discussions.









