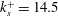1. Introduction
1.1. Unsteady flow
Unsteady flows, in which the bulk velocity of wall-bounded flows or the free-stream velocity of boundary layer flows vary with time, are of general interest because they are encountered in many engineering applications. Examples include nuclear and conventional power plant, blood flow in large arteries, combustion engines and unsteady flows in the natural environment, such as those occurring under sea waves. Previous studies of non-periodic transient flows over smooth surfaces include Greenblatt & Moss (Reference Greenblatt and Moss1999, Reference Greenblatt and Moss2004), He & Jackson (Reference He and Jackson2000), Chung (Reference Chung2005), He, Ariyaratne & Vardy (Reference He, Ariyaratne and Vardy2008, Reference He, Ariyaratne and Vardy2011), Seddighi et al. (Reference Seddighi, He, Orlandi and Vardy2011) and Jung & Chung (Reference Jung and Chung2012). It has been established that, in a temporally accelerating flow over smooth surfaces, the unsteady-flow behaviour is largely associated with the response of turbulence. Initially, there is a short period when turbulence is effectively ‘frozen’, which is followed by response of turbulence, first in the streamwise component in the near-wall region. Later, the streamwise turbulent energy is redistributed into other two components. The response of the turbulence then propagates into the core of the flow with progressively longer delays.
Recently, direct numerical simulations (DNS) of transient channel flow over a smooth wall were reported by He & Seddighi (Reference He and Seddighi2013, hereafter HS2013), Seddighi et al. (Reference Seddighi, He, Vardy and Orlandi2014) and He & Seddighi (Reference He and Seddighi2015). These studies brought a novel perspective on the flow behaviour, showing that, even though the initial flow is turbulent, the transient flow process is effectively a laminar–turbulent transition, similar to bypass transition in a boundary layer (e.g. Jacobs & Durbin Reference Jacobs and Durbin2001). It has been shown that, for the transient flow following a near-step increase in mass flow rate, the flow initially responds like a ‘plug flow’ – the velocity increases uniformly across the flow domain except in the vicinity of the wall where a thin boundary layer of high strain rates is formed due to the ‘no-slip’ boundary condition on the wall. This boundary layer will then develop into the core of the flow with time. HS2013 have shown that the flow within the developing boundary layer undergoes three distinct phases. Initially (pre-transition) the flow is laminar-like and the pre-existing turbulent structures are modulated, resulting in elongated streaks. This leads to a strong and continuous increase in the streamwise velocity fluctuation, but little change in the other two components. The flow then undergoes transition as isolated turbulent spots are generated, which spread and merge with each other. The turbulent spots eventually cover the entire surface of the wall when the flow is fully turbulent.
Seddighi et al. (Reference Seddighi, He, Vardy and Orlandi2014) showed that a similar transition process occurs in a slowly accelerating flow, in which the period of flow acceleration is longer than the period of pre-transition. This similarity is significant given the contrasting features of the two types of mean flow unsteadiness. In the step-increase flow, a boundary layer of high shear rate is produced nearly instantly on the wall, closely resembling a uniform flow encountering a flat surface and hence resulting in a boundary layer with a high velocity gradient at its leading edge. By contrast, the accelerating flow causes a continuing change of velocity gradient adjacent to the wall, which propagates into the flow field with time, resulting in a gradually developing boundary layer. There are, however, quantitative differences in the detailed turbulent behaviour of the two flows; in particular, transition is much delayed in the case of the accelerating flow compared to the step-increase flow.
More recently, He & Seddighi (Reference He and Seddighi2015) systematically varied the initial and final Reynolds numbers of the near-step transition flows. It was shown that, for all conditions, the transient flow is characterised by laminar–turbulent transition, which exhibits itself clearly in the flow statistics. This is despite the fact that when the final/initial Reynolds number ratio is low (such as 1.1), the flow does not exhibit either elongated streaks or isolated turbulent spots, which are present when the final/initial Reynolds number ratio is high. The time-developing boundary layer in the pre-transition phase follows closely the Stokes solution for a transient laminar boundary layer.
Relaminarisation has been observed in accelerating boundary layer flows. A well-known salient influence of favourable pressure gradient (FPG), which has been confirmed by many researchers, is stabilisation of the near-wall streaks through damping of the wall-normal and spanwise fluctuations (Blackwelder & Kovasznay Reference Blackwelder and Kovasznay1972; Piomelli, Balaras & Pascarelli Reference Piomelli, Balaras and Pascarelli2000; Bourassa & Thomas Reference Bourassa and Thomas2009; Piomelli & Yuan Reference Piomelli and Yuan2013). Recently, Piomelli & Yuan (Reference Piomelli and Yuan2013) carried out detailed DNS and large-eddy simulations (LES) to study the influence of FPG on a spatially developing boundary layer. The results showed a strong flow relaminarisation in the region of high acceleration, followed by re-transition to turbulence after the end of the FPG. They observed a reduction in friction, a reduction in the wall-normal and spanwise fluctuations (while streamwise fluctuations remain unchanged), and the flow approaching a one-dimensional (1D) turbulence state with decreasing burst frequency. The authors attributed the reduction of the wall-normal and spanwise fluctuations to a reduction in the pressure fluctuations and energy redistribution due to the influence of mean velocity gradient. The reduction incurred in the wall-normal fluctuations directly influences the generation and stability of streaks by reducing the wall-normal advection of the spanwise vorticity, and hence causes the streaks to be more stable and quasi-laminar-like. Piomelli & Yuan (Reference Piomelli and Yuan2013) also found that introducing roughness on the wall results in increased wall-normal fluctuations, leading to more isotropic near-wall turbulence and a more energetic inner layer, thereby retarding flow relaminarisation.
1.2. Roughness-induced transition
Laminar flow can take various transition paths to turbulence depending on the flow and boundary conditions. In general, the process can be dominated by either amplification of the so-called Tollmien–Schlichting (TS) instability waves (natural transition), or bypass of such waves in part or full (bypass transition). Transition is influenced by surface roughness. Aeronautical applications are important examples of external flows in which roughness-induced transition is of imperative consideration because of its potential significant influence on aerodynamic performance and heat transfer; the latter can be profound in supersonic and hypersonic flows (Muppidi & Mahesh Reference Muppidi and Mahesh2012). Most previous studies of the influence of roughness on transition involve either two-dimensional (2D) roughness strips or three-dimensional (3D) roughness, and, for the latter, either an isolated element or a spanwise array of elements. There are fewer studies on distributed 3D elements.
Correlation methods can predict the transition induced in the wake of roughness elements (Tani Reference Tani1969; Reshotko Reference Reshotko2008). The prediction is based on roughness-based Reynolds number,
![]() $\mathit{Re}_{k}$
, and the ratio of the roughness height (
$\mathit{Re}_{k}$
, and the ratio of the roughness height (
![]() $k$
) to either boundary layer length scale or displacement thickness. Here,
$k$
) to either boundary layer length scale or displacement thickness. Here,
![]() $\mathit{Re}_{k}=ku_{k}/{\it\nu}$
, where
$\mathit{Re}_{k}=ku_{k}/{\it\nu}$
, where
![]() $u_{k}$
is the Blasius streamwise velocity component at the height of the roughness. However, this approach is neither accurate for distributed 3D roughness, nor provides detailed information on the transition mechanism. In fact, such an approach provides no information on the influence of roughness until
$u_{k}$
is the Blasius streamwise velocity component at the height of the roughness. However, this approach is neither accurate for distributed 3D roughness, nor provides detailed information on the transition mechanism. In fact, such an approach provides no information on the influence of roughness until
![]() $\mathit{Re}_{k}$
reaches
$\mathit{Re}_{k}$
reaches
![]() $\mathit{Re}_{k_{critical}}$
, at which point the roughness element starts to affect the transition.
$\mathit{Re}_{k_{critical}}$
, at which point the roughness element starts to affect the transition.
Traditionally, studies of transition in the presence of roughness (in particular 2D elements) were mostly based on TS arguments (e.g. Klebanoff & Tidstrom Reference Klebanoff and Tidstrom1972), in which roughness influences one or more of the three stages of the transition, namely the generation of linear instability waves (receptivity), the linear growth of such waves and the nonlinear breakdown (Nayfeh & Ashour Reference Nayfeh and Ashour1994). However, since the 1980s, it has been shown by many researchers that, for 3D roughness elements, transient growth is an alternative possible explanation of some roughness-induced transition (Reshotko Reference Reshotko1984, Reference Reshotko2008; Reshotko & Tumin Reference Reshotko and Tumin2004; Szumbarski & Floryan Reference Szumbarski and Floryan2006).
Transient growth is physically attributed to the lift-up mechanism described by Landahl (Reference Landahl1980), in which longitudinal streaky structures in the flow are induced by hairpin vortices that are quasi-streamwise, counter-rotating and stationary. In fact, redistribution of momentum carried by hairpin vortices, from the free stream into the boundary layer, can cause the steady velocity disturbances to amplify algebraically prior to exponential decay. The redistribution process can result in excess energy in the form of low- and high-speed streaks, which may become unstable, leading to breakdown to turbulence before the viscous decay occurs. Examples in which this process occurs are the bypass transition due to the existence of high free-stream turbulence intensity, and the transition induced by 3D roughness. Mathematically, transient growth refers to algebraic amplification (rather than the exponential growth occurring in TS-wave-type) followed by exponential decay resulting from the coupling of quasi-streamwise and slightly damped Orr–Sommerfeld and Squire modes (Reshotko & Tumin Reference Reshotko and Tumin2004).
Among the earliest studies on the physics of flow over isolated 3D roughness, Gregory & Walker (Reference Gregory and Walker1956) carried out smoke and China-clay visualisations of the boundary layer flow passing an isolated cylindrical pimple of relatively large height. They observed that horseshoe and hairpin structures exist around the roughness element. Their basic observations have been enhanced in numerous subsequent studies. Among those, Acarlar & Smith (Reference Acarlar and Smith1987) conducted comprehensive hot-film measurements and hydrogen-bubble and dye visualisations in the wake of a hemisphere protuberance in a free-surface water channel at
![]() $30\leqslant \mathit{Re}_{k}\leqslant 3400$
, to study the formation and evolution of hairpin vortices shed behind the isolated element in the laminar boundary layer. For relatively large roughness Reynolds number (
$30\leqslant \mathit{Re}_{k}\leqslant 3400$
, to study the formation and evolution of hairpin vortices shed behind the isolated element in the laminar boundary layer. For relatively large roughness Reynolds number (
![]() $\mathit{Re}_{k}\geqslant 120$
), their visualisations showed the presence of two types of vortex, namely standing and hairpin types. Whereas the former are generated at the upstream stagnation point of the roughness, the latter are formed periodically in the low-pressure recirculation region just after the isolated roughness, and shedding downstream for the flow cases.
$\mathit{Re}_{k}\geqslant 120$
), their visualisations showed the presence of two types of vortex, namely standing and hairpin types. Whereas the former are generated at the upstream stagnation point of the roughness, the latter are formed periodically in the low-pressure recirculation region just after the isolated roughness, and shedding downstream for the flow cases.
Detailed investigations of the structure of hairpin vortices induced by isolated roughness at high-speed flows have been reported in several studies (Redford, Sandham & Roberts Reference Redford, Sandham and Roberts2010; Bernardini, Pirozzoli & Orlandi Reference Bernardini, Pirozzoli and Orlandi2012; Iyer & Mahesh Reference Iyer and Mahesh2013). Although transition in supersonic and hypersonic flow regimes is further influenced by compressibility and temperature effects, many features of the transition mechanisms are similar to those of low-speed incompressible flows (Redford et al. Reference Redford, Sandham and Roberts2010; Bernardini et al. Reference Bernardini, Pirozzoli and Orlandi2012). These include the formation of unsteady hairpin structures after the roughness and lift-up process, and the influence of the hairpin structures on destabilising the shear layer over the roughness element. Hence, studying the roughness-induced transition mechanism at low-speed flow can shed some light on flow behaviour and structures expected to occur in high-speed flows.
In contrast to isolated roughness, there are few studies on roughness-induced transition involving distributed 3D elements. In the few studies that have been carried out, the majority have used a spanwise array of roughness elements and the relative height of the roughness has been large. Recently, the experiments of Downs, White & Denissen (Reference Downs, White and Denissen2008) and Kuester & White (Reference Kuester and White2013) and the DNS simulations of Drews et al. (Reference Drews, Downs, Doolittle, Goldstein and White2011) and Drews (Reference Drews2012) were carried out to study roughness-induced transition due to patches of random elements in a Blasius boundary layer. The results showed the occurrence of transient growth in the roughness-induced disturbances, as observed previously for cases of isolated roughness. It was also found that disturbances are initially generated by the largest-amplitude elements (with height approximately half of the boundary layer thickness) and subsequently undergo transient growth. Moreover, the smaller-amplitude elements in the roughness patch influence the process through a shielding effect that reduces the strength of the wakes generated by the largest elements. Subcritical disturbance amplification is generally observed at low frequencies, resulting in bypass transition, similar to that occurring in boundary layers over smooth walls with moderate to high free-stream turbulence intensity.
1.3. Present work
In the present study, DNS is used to investigate a ‘turbulent–turbulent’ transient flow in a channel consisting of a rough bottom wall made of distributed roughness elements of relatively small height. The flow is initially steady in the transitionally rough regime at
![]() $k_{s}^{+}=14.5$
. The flow rate is then suddenly increased to a much higher-level flow condition at
$k_{s}^{+}=14.5$
. The flow rate is then suddenly increased to a much higher-level flow condition at
![]() $k_{s}^{+}=41.5$
, once steady conditions are reached. The focus of the study is to investigate the transient behaviour following the near-step increase in flow rate. It is shown that this turbulent–turbulent transient flow over the pyramid rough wall undergoes a process that resembles the roughness-induced laminar–turbulent transition. The transition is found to be in the form of a single cycle of birth, evolution and breakdown of strong primary counter-rotating hairpin structures, alongside the formation and breakdown of strong and uniformly distributed high- and low-speed streaks. In addition, the developments of the flow and turbulence statistics in an unsteady flow over a rough surface are interpreted by relating them to the newly established transition process.
$k_{s}^{+}=41.5$
, once steady conditions are reached. The focus of the study is to investigate the transient behaviour following the near-step increase in flow rate. It is shown that this turbulent–turbulent transient flow over the pyramid rough wall undergoes a process that resembles the roughness-induced laminar–turbulent transition. The transition is found to be in the form of a single cycle of birth, evolution and breakdown of strong primary counter-rotating hairpin structures, alongside the formation and breakdown of strong and uniformly distributed high- and low-speed streaks. In addition, the developments of the flow and turbulence statistics in an unsteady flow over a rough surface are interpreted by relating them to the newly established transition process.
The paper is organised as follows. The numerical method is described in § 2. The roughness topology, flow conditions and the methodology used to analyse the data are presented in § 3. The results and discussions are presented in § 4 and the main conclusions are stated in § 5.
2. Numerical methods
DNS is performed using an ‘in-house’ code (Seddighi Reference Seddighi2011; He & Seddighi Reference He and Seddighi2013) modified for implementing the 3D roughness. The governing equations are written in dimensionless form, normalised using the channel half-height (
![]() ${\it\delta}$
) for length,
${\it\delta}$
) for length,
![]() $U_{c}$
(centreline laminar Poiseuille velocity) for velocity, and
$U_{c}$
(centreline laminar Poiseuille velocity) for velocity, and
![]() ${\it\rho}U_{c}^{2}$
for pressure:
${\it\rho}U_{c}^{2}$
for pressure:
The Reynolds number is defined as
![]() $\mathit{Re}_{c}={\it\delta}U_{c}/{\it\nu}$
. However, for ease of explanation of the results, unless otherwise stated, the times presented in this paper are rescaled using the bulk velocity of the initial flow (
$\mathit{Re}_{c}={\it\delta}U_{c}/{\it\nu}$
. However, for ease of explanation of the results, unless otherwise stated, the times presented in this paper are rescaled using the bulk velocity of the initial flow (
![]() $U_{b0}$
) as the characteristic velocity. The pressure gradient is split into two components, namely
$U_{b0}$
) as the characteristic velocity. The pressure gradient is split into two components, namely
![]() ${\it\Pi}$
and
${\it\Pi}$
and
![]() $\partial p^{\ast }/\partial x_{i}^{\ast }$
. The former is the spatially uniform component of the streamwise pressure gradient required to balance the resistance due to friction and form drag (i.e. the value that would be needed to maintain a constant mass flow rate). The
$\partial p^{\ast }/\partial x_{i}^{\ast }$
. The former is the spatially uniform component of the streamwise pressure gradient required to balance the resistance due to friction and form drag (i.e. the value that would be needed to maintain a constant mass flow rate). The
![]() $\partial p^{\ast }/\partial x_{i}^{\ast }$
component is a fluctuating component that varies both spatially and with time due to turbulence and flow heterogeneity. A second-order central finite difference method is used to discretise the spatial derivatives of the governing equations on a rectangular grid, where a 3D staggered mesh is employed with a non-uniform spacing in the direction normal to the wall. For time advancement, a low-storage third-order Runge–Kutta scheme is used for the nonlinear terms, and a second-order Crank–Nicolson scheme is used for the viscous terms. These schemes are combined with a fractional-step method described by Kim & Moin (Reference Kim and Moin1985) and Orlandi (Reference Orlandi2001). The Poisson equation for the pressure is solved by an efficient fast Fourier transform (FFT) (Orlandi Reference Orlandi2001). The message-passing interface (MPI) is used to parallelise the code. The channel consists of a smooth top surface and a close-packed pyramid-roughened bottom surface (§ 3).
$\partial p^{\ast }/\partial x_{i}^{\ast }$
component is a fluctuating component that varies both spatially and with time due to turbulence and flow heterogeneity. A second-order central finite difference method is used to discretise the spatial derivatives of the governing equations on a rectangular grid, where a 3D staggered mesh is employed with a non-uniform spacing in the direction normal to the wall. For time advancement, a low-storage third-order Runge–Kutta scheme is used for the nonlinear terms, and a second-order Crank–Nicolson scheme is used for the viscous terms. These schemes are combined with a fractional-step method described by Kim & Moin (Reference Kim and Moin1985) and Orlandi (Reference Orlandi2001). The Poisson equation for the pressure is solved by an efficient fast Fourier transform (FFT) (Orlandi Reference Orlandi2001). The message-passing interface (MPI) is used to parallelise the code. The channel consists of a smooth top surface and a close-packed pyramid-roughened bottom surface (§ 3).
The roughness is treated using an immersed boundary method (IBM) described in detail by Orlandi and co-workers (see e.g. Orlandi & Leonardi Reference Orlandi and Leonardi2006). The method is a revised IBM approach initially developed by Fadlun et al. (Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000), and later amended by Orlandi and co-workers mainly for the treatment of the first point away from the wall boundary. The method efficiently handles complex geometry with regular grids through the introduction of a body force in the momentum equations. Implementing the roughness by this method avoids the need for body-fitted curvilinear or unstructured meshes and hence leads to a big reduction in simulation cost. In the method, the velocities of the nodes inside the roughness element are set equal to the roughness velocity (zero in the case of fixed roughness, such as that used herein). Since in the case of complex geometry the computational nodes do not necessarily coincide with the roughness boundary, this will result in prescribing the geometry in a stepwise way (figure 1). In the revised method due to Orlandi and co-workers, consideration is given to use the actual distance between the roughness element and the first computational node away from the roughness. The terms (mainly second derivatives) in the discretised Navier–Stokes equations are modified to enforce the boundary condition on the roughness body accordingly. For any direction, the coefficients of the second derivatives based on the real distance can be prescribed as
where ‘
![]() $i-1$
’, ‘
$i-1$
’, ‘
![]() $i$
’ and ‘
$i$
’ and ‘
![]() $i+1$
’ denote the nodes on the boundary and the first and the second nodes away from the boundary, respectively (figure 1). At the boundary nodes,
$i+1$
’ denote the nodes on the boundary and the first and the second nodes away from the boundary, respectively (figure 1). At the boundary nodes,
![]() $u_{i-1}=V_{b}=0$
. Also,
$u_{i-1}=V_{b}=0$
. Also,
![]() ${\it\Delta}_{1}$
is the real distance between the node ‘
${\it\Delta}_{1}$
is the real distance between the node ‘
![]() $i$
’ and its neighbour ‘
$i$
’ and its neighbour ‘
![]() $i-1$
’, and
$i-1$
’, and
![]() ${\it\Delta}_{2}$
is the regular mesh spacing between the node ‘
${\it\Delta}_{2}$
is the regular mesh spacing between the node ‘
![]() $i$
’ and ‘
$i$
’ and ‘
![]() $i+1$
’. This method has been validated for several 2D and 3D roughness elements against experimental data. Examples of such studies are Orlandi & Leonardi (Reference Orlandi and Leonardi2006) for 3D cubes and 2D ribs, Orlandi, Leonardi & Antonia (Reference Orlandi, Leonardi and Antonia2006) for circular bars, Bailon-Cuba, Leonardi & Castillo (Reference Bailon-Cuba, Leonardi and Castillo2009) for a wedge, and Orlandi (Reference Orlandi2011) for triangular roughness.
$i+1$
’. This method has been validated for several 2D and 3D roughness elements against experimental data. Examples of such studies are Orlandi & Leonardi (Reference Orlandi and Leonardi2006) for 3D cubes and 2D ribs, Orlandi, Leonardi & Antonia (Reference Orlandi, Leonardi and Antonia2006) for circular bars, Bailon-Cuba, Leonardi & Castillo (Reference Bailon-Cuba, Leonardi and Castillo2009) for a wedge, and Orlandi (Reference Orlandi2011) for triangular roughness.

Figure 1. Sketch of a typical roughness and the computational nodes.
3. Geometry, flow conditions and statistical averaging
3.1. Geometry and flow conditions
The channel consists of a smooth top surface and a close-packed pyramid-roughened bottom surface (Figure 2). The slope angle of the lateral edge of the pyramid with the horizontal plane is
![]() ${\it\alpha}\approx 18.4^{\circ }$
and the height of the roughness is
${\it\alpha}\approx 18.4^{\circ }$
and the height of the roughness is
![]() $k_{t}/{\it\delta}=0.05$
, where
$k_{t}/{\it\delta}=0.05$
, where
![]() $k_{t}$
is peak-to-trough roughness height. The initial and final Reynolds numbers of the transient flow are
$k_{t}$
is peak-to-trough roughness height. The initial and final Reynolds numbers of the transient flow are
![]() $\mathit{Re}_{0}=2800$
and
$\mathit{Re}_{0}=2800$
and
![]() $\mathit{Re}_{1}=7400$
, respectively, where
$\mathit{Re}_{1}=7400$
, respectively, where
![]() $\mathit{Re}={\it\delta}U_{b}/{\it\nu}$
, with
$\mathit{Re}={\it\delta}U_{b}/{\it\nu}$
, with
![]() $U_{b}$
the bulk velocity and
$U_{b}$
the bulk velocity and
![]() ${\it\nu}$
the fluid kinematic viscosity. The Reynolds-number values are chosen to be similar to those of previous studies with a smooth wall for ease of comparison (HS2013; Seddighi et al.
Reference Seddighi, He, Vardy and Orlandi2014). In addition to the unsteady-flow simulation, four steady-flow (stationary flow) conditions were simulated, two for the smooth wall and two for the rough wall (table 1). The two rough-wall steady-flow cases, PA2800 and PA7400, correspond to the initial condition and final condition, respectively, of the unsteady-flow simulation. The two smooth-wall steady-flow cases, S3500 and S12600, have values of
${\it\nu}$
the fluid kinematic viscosity. The Reynolds-number values are chosen to be similar to those of previous studies with a smooth wall for ease of comparison (HS2013; Seddighi et al.
Reference Seddighi, He, Vardy and Orlandi2014). In addition to the unsteady-flow simulation, four steady-flow (stationary flow) conditions were simulated, two for the smooth wall and two for the rough wall (table 1). The two rough-wall steady-flow cases, PA2800 and PA7400, correspond to the initial condition and final condition, respectively, of the unsteady-flow simulation. The two smooth-wall steady-flow cases, S3500 and S12600, have values of
![]() $\mathit{Re}_{{\it\tau}}$
similar to the corresponding rough-wall steady-flow cases (
$\mathit{Re}_{{\it\tau}}$
similar to the corresponding rough-wall steady-flow cases (
![]() ${\sim}$
205 and
${\sim}$
205 and
![]() ${\sim}$
670). Here,
${\sim}$
670). Here,
![]() $\mathit{Re}_{{\it\tau}}={\it\delta}_{t}u_{{\it\tau}}/{\it\nu}$
, where
$\mathit{Re}_{{\it\tau}}={\it\delta}_{t}u_{{\it\tau}}/{\it\nu}$
, where
![]() $u_{{\it\tau}}$
is the friction velocity and
$u_{{\it\tau}}$
is the friction velocity and
![]() ${\it\delta}_{t}$
is the effective channel half-height, defined as the distance between the roughness crest and the location where the turbulent shear stress is zero. For the rough-wall cases, the friction velocity of the lower (rough wall) is used; for the smooth-wall cases, the average of the upper and lower wall friction velocities is used. Height
${\it\delta}_{t}$
is the effective channel half-height, defined as the distance between the roughness crest and the location where the turbulent shear stress is zero. For the rough-wall cases, the friction velocity of the lower (rough wall) is used; for the smooth-wall cases, the average of the upper and lower wall friction velocities is used. Height
![]() ${\it\delta}_{t}$
coincides with the geometrical channel half-height (
${\it\delta}_{t}$
coincides with the geometrical channel half-height (
![]() ${\it\delta}$
) for the smooth-wall cases, while it is slightly higher than
${\it\delta}$
) for the smooth-wall cases, while it is slightly higher than
![]() ${\it\delta}$
for the rough-wall cases (table 1).
${\it\delta}$
for the rough-wall cases (table 1).

Figure 2. (a) Rough-wall roughness structure; (b)
![]() $x$
–
$x$
–
![]() $z$
plane view of one wavelength of roughness; (c) geometric parameters for roughness pyramid,
$z$
plane view of one wavelength of roughness; (c) geometric parameters for roughness pyramid,
![]() $k_{t}=0.05({\it\delta})$
,
$k_{t}=0.05({\it\delta})$
,
![]() ${\it\lambda}=0.3({\it\delta})$
and
${\it\lambda}=0.3({\it\delta})$
and
![]() ${\it\alpha}\approx 18.4^{\circ }$
.
${\it\alpha}\approx 18.4^{\circ }$
.
Table 1. Details of the steady-flow cases simulated.


Figure 3. Roughness function versus equivalent roughness height.
The mesh points, number of roughness elements and computational domain are the same for all simulations: 1024, 32 and 9.6(
![]() ${\it\delta}$
), respectively, in the streamwise direction; 720, 15 and 4.5(
${\it\delta}$
), respectively, in the streamwise direction; 720, 15 and 4.5(
![]() ${\it\delta}$
) in the spanwise direction. The streamwise and spanwise wavelengths of the roughness are set to
${\it\delta}$
) in the spanwise direction. The streamwise and spanwise wavelengths of the roughness are set to
![]() ${\it\lambda}_{x}={\it\lambda}_{z}=0.3$
(figure 2). In the wall-normal direction, 240 mesh points are used, of which 24 points are equally spaced over the roughness height,
${\it\lambda}_{x}={\it\lambda}_{z}=0.3$
(figure 2). In the wall-normal direction, 240 mesh points are used, of which 24 points are equally spaced over the roughness height,
![]() $k_{t}$
. Periodicity is imposed in both the streamwise and spanwise directions and a no-slip condition is used on all rigid surfaces. The first point away from the base of the rough wall,
$k_{t}$
. Periodicity is imposed in both the streamwise and spanwise directions and a no-slip condition is used on all rigid surfaces. The first point away from the base of the rough wall,
![]() $y_{1}$
, is located at
$y_{1}$
, is located at
![]() $y_{1}/{\it\delta}=0.00106$
, which corresponds to
$y_{1}/{\it\delta}=0.00106$
, which corresponds to
![]() $y_{1}^{+}\approx 0.2$
and
$y_{1}^{+}\approx 0.2$
and
![]() $y_{1}^{+}\approx 0.6$
for PA2800 and PA7400, respectively. The code for the smooth wall has been validated against well-known DNS benchmark data and shows close agreement (Seddighi Reference Seddighi2011; Seddighi et al.
Reference Seddighi, He, Orlandi and Vardy2011; He & Seddighi Reference He and Seddighi2013).
$y_{1}^{+}\approx 0.6$
for PA2800 and PA7400, respectively. The code for the smooth wall has been validated against well-known DNS benchmark data and shows close agreement (Seddighi Reference Seddighi2011; Seddighi et al.
Reference Seddighi, He, Orlandi and Vardy2011; He & Seddighi Reference He and Seddighi2013).
For the steady-flow rough-wall cases, two validation exercises have been carried out. First, a mesh refinement study was performed to ensure that the mesh used is sufficiently fine. For this purpose, friction factor and wall-normal profiles of Reynolds stress obtained using the final mesh were compared with corresponding results obtained using meshes that are two times coarser in the streamwise and spanwise directions. Second, the roughness function,
![]() ${\rm\Delta}U^{+}$
, which represents the effect of roughness (defined below), obtained from the simulations has been compared with the steady-flow experimental data of Schultz & Flack (Reference Schultz and Flack2009), who used similar pyramid roughness geometries in their experiments involving laser Doppler velocimetry measurements in a boundary layer flow. The results show close agreement (figure 3). To obtain the equivalent roughness height,
${\rm\Delta}U^{+}$
, which represents the effect of roughness (defined below), obtained from the simulations has been compared with the steady-flow experimental data of Schultz & Flack (Reference Schultz and Flack2009), who used similar pyramid roughness geometries in their experiments involving laser Doppler velocimetry measurements in a boundary layer flow. The results show close agreement (figure 3). To obtain the equivalent roughness height,
![]() $k_{s}$
, the
$k_{s}$
, the
![]() ${\rm\Delta}U^{+}$
result from the highest-Reynolds-number steady-flow simulation (PA7400) is used in the following formula (equation (1.3) in Krogstad et al.
Reference Krogstad, Andersson, Bakken and Ashrafian2005), from which
${\rm\Delta}U^{+}$
result from the highest-Reynolds-number steady-flow simulation (PA7400) is used in the following formula (equation (1.3) in Krogstad et al.
Reference Krogstad, Andersson, Bakken and Ashrafian2005), from which
![]() $k_{s}\approx 1.5k_{t}$
is obtained:
$k_{s}\approx 1.5k_{t}$
is obtained:
Here
![]() ${\rm\Delta}U^{+}=\langle \overline{u_{s}}\rangle ^{+}-\langle \overline{u_{r}}\rangle ^{+}$
, and
${\rm\Delta}U^{+}=\langle \overline{u_{s}}\rangle ^{+}-\langle \overline{u_{r}}\rangle ^{+}$
, and
![]() $\langle \overline{u_{s}}\rangle ^{+}$
and
$\langle \overline{u_{s}}\rangle ^{+}$
and
![]() $\langle \overline{u_{r}}\rangle ^{+}$
are the mean streamwise velocity (defined in § 3.2) normalised by friction velocity for the smooth and rough walls, respectively;
$\langle \overline{u_{r}}\rangle ^{+}$
are the mean streamwise velocity (defined in § 3.2) normalised by friction velocity for the smooth and rough walls, respectively;
![]() ${\it\kappa}$
is the von Kármán constant; and
${\it\kappa}$
is the von Kármán constant; and
![]() $B$
is the smooth-wall log-law intercept. The intercept constant
$B$
is the smooth-wall log-law intercept. The intercept constant
![]() $B$
is taken to be 5.39, according to the value determined from figure 4. The obtained
$B$
is taken to be 5.39, according to the value determined from figure 4. The obtained
![]() $k_{s}/k_{t}$
ratio of 1.5 is in agreement with other studies on fully rough pyramid geometry (Schultz & Flack Reference Schultz and Flack2009; Hong, Katz & Schultz Reference Hong, Katz and Schultz2011; Hong et al.
Reference Hong, Katz, Meneveau and Schultz2012), and has then been applied to all rough cases studied.
$k_{s}/k_{t}$
ratio of 1.5 is in agreement with other studies on fully rough pyramid geometry (Schultz & Flack Reference Schultz and Flack2009; Hong, Katz & Schultz Reference Hong, Katz and Schultz2011; Hong et al.
Reference Hong, Katz, Meneveau and Schultz2012), and has then been applied to all rough cases studied.
3.2. Statistics
For the steady-flow cases, DNS was first run until the flow is fully developed. The simulation is then continued in order to obtain approximately 50 independent flow realisations to enable ensemble averaging. The simulations of the transient flow begin from a fully developed steady turbulent flow,
![]() $\mathit{Re}_{0}=2800$
. At time
$\mathit{Re}_{0}=2800$
. At time
![]() $t^{\ast }\,(=t/({\it\delta}/U_{b0}))=0$
(where
$t^{\ast }\,(=t/({\it\delta}/U_{b0}))=0$
(where
![]() $U_{b0}$
is the bulk velocity for the initial flow), the flow rate is increased linearly to the final
$U_{b0}$
is the bulk velocity for the initial flow), the flow rate is increased linearly to the final
![]() $\mathit{Re}_{1}=7400$
within a very short time period of
$\mathit{Re}_{1}=7400$
within a very short time period of
![]() ${\rm\Delta}t^{\ast }\sim 0.08$
, and the simulation continues well beyond the time when the flow has again become fully developed. The unsteady simulations are repeated six times to enable calculations of flow statistics using ensemble averaging. The initial flow for each of the unsteady simulations is taken from different time instants of the corresponding steady-flow simulation, with a large time interval (approximately 10 times the integral time scale of the initial flow) between them in order to ensure that the flow fields are independent of each other. In the following, the averaging procedures that are carried out to calculate mean and turbulent statistics in this paper are described.
${\rm\Delta}t^{\ast }\sim 0.08$
, and the simulation continues well beyond the time when the flow has again become fully developed. The unsteady simulations are repeated six times to enable calculations of flow statistics using ensemble averaging. The initial flow for each of the unsteady simulations is taken from different time instants of the corresponding steady-flow simulation, with a large time interval (approximately 10 times the integral time scale of the initial flow) between them in order to ensure that the flow fields are independent of each other. In the following, the averaging procedures that are carried out to calculate mean and turbulent statistics in this paper are described.

Figure 4. Mean velocity and sample diagnostic function used for origin detection for the case PA7400; (a) variation of
![]() $({\it\Xi}-1/{\it\kappa})$
for the origin detection; (b) inner scaled mean velocity using
$({\it\Xi}-1/{\it\kappa})$
for the origin detection; (b) inner scaled mean velocity using
![]() ${\it\varepsilon}_{d}=0.03$
.
${\it\varepsilon}_{d}=0.03$
.
3.2.1. Ensemble averaging
In principle, ensemble averaging is carried out over a number of samples of flow field at different time instants, and is denoted by ‘
![]() $\,\bar{\cdot }\,$
’. In practice, making use of the ergodic hypothesis, the following procedure is taken to obtain an ensemble-averaged quantity.
$\,\bar{\cdot }\,$
’. In practice, making use of the ergodic hypothesis, the following procedure is taken to obtain an ensemble-averaged quantity.
For a smooth wall, an ensemble average of quantity
![]() ${\it\phi}$
at any
${\it\phi}$
at any
![]() $y$
elevation consists of data at all computational points in the homogeneous (streamwise and spanwise) directions, and for all repeated realisations,
$y$
elevation consists of data at all computational points in the homogeneous (streamwise and spanwise) directions, and for all repeated realisations,
where
![]() $M_{1}$
and
$M_{1}$
and
![]() $N_{1}$
are the numbers of total data points, in the streamwise and spanwise directions, respectively, and
$N_{1}$
are the numbers of total data points, in the streamwise and spanwise directions, respectively, and
![]() $L$
is the number of repeated runs.
$L$
is the number of repeated runs.
For a rough wall, an ensemble average of the quantity
![]() ${\it\phi}$
consists of the data at all points at the same relative position with respect to the pyramid wavelength (and in the same wall-parallel plane), for all repeated realisations. This produces spatially varying turbulence quantities within a roughness wavelength. The ensemble average of
${\it\phi}$
consists of the data at all points at the same relative position with respect to the pyramid wavelength (and in the same wall-parallel plane), for all repeated realisations. This produces spatially varying turbulence quantities within a roughness wavelength. The ensemble average of
![]() ${\it\phi}$
for a rough wall at any
${\it\phi}$
for a rough wall at any
![]() $y$
elevation reads
$y$
elevation reads
where
![]() $x/{\it\lambda}$
and
$x/{\it\lambda}$
and
![]() $z/{\it\lambda}$
are, respectively, the streamwise and spanwise relative locations in a roughness wavelength (see figure 2
b), and
$z/{\it\lambda}$
are, respectively, the streamwise and spanwise relative locations in a roughness wavelength (see figure 2
b), and
![]() $M_{2}$
and
$M_{2}$
and
![]() $N_{2}$
are the numbers of roughness elements in the streamwise and spanwise directions, respectively.
$N_{2}$
are the numbers of roughness elements in the streamwise and spanwise directions, respectively.
Using (3.2) and (3.3), the fluctuating velocities for both smooth and rough walls are defined as
![]() $u_{s}^{\prime }=u_{s}-\overline{u}_{s}$
; and the associated Reynolds stresses,
$u_{s}^{\prime }=u_{s}-\overline{u}_{s}$
; and the associated Reynolds stresses,
![]() $\overline{u_{i}^{\prime }u_{j}^{\prime }}$
, are computed using (3.2) or (3.3) for smooth or rough walls, respectively. Here
$\overline{u_{i}^{\prime }u_{j}^{\prime }}$
, are computed using (3.2) or (3.3) for smooth or rough walls, respectively. Here
![]() $s,i,j=1,2,3$
for the streamwise, wall-normal and spanwise velocity components, respectively, which are also denoted as
$s,i,j=1,2,3$
for the streamwise, wall-normal and spanwise velocity components, respectively, which are also denoted as
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
.
$w$
.
3.2.2. Spatial averaging
The ensemble-averaged turbulent quantities of a rough wall can be further averaged over a plane to produce ‘spatially averaged’ quantities, which are a function of
![]() $y$
only. Accordingly, any quantity
$y$
only. Accordingly, any quantity
![]() $\overline{{\it\phi}}$
defined with (3.3) is further averaged over the roughness wavelength at each
$\overline{{\it\phi}}$
defined with (3.3) is further averaged over the roughness wavelength at each
![]() $y$
elevation,
$y$
elevation,
where
![]() $M_{3}$
and
$M_{3}$
and
![]() $N_{3}$
are the number of points in each roughness element in the streamwise and spanwise directions, respectively. They are referred to as spatially averaged turbulent quantities. Note that the ensemble-averaged quantities for a smooth wall are the same as their spatially averaged equivalent and are also denoted by
$N_{3}$
are the number of points in each roughness element in the streamwise and spanwise directions, respectively. They are referred to as spatially averaged turbulent quantities. Note that the ensemble-averaged quantities for a smooth wall are the same as their spatially averaged equivalent and are also denoted by
![]() $\langle \,\bar{\cdot }\,\rangle$
. The root mean square (r.m.s.) of turbulent velocity fluctuations is defined as
$\langle \,\bar{\cdot }\,\rangle$
. The root mean square (r.m.s.) of turbulent velocity fluctuations is defined as
New statistical quantities can be defined for turbulent–spatial fluctuations to capture fluctuating velocities due to both turbulent fluctuations and spatial fluctuations resulting from roughness geometry. The fluctuating velocities are defined as
![]() $u_{s}^{\prime \prime }=u_{s}-\langle \overline{u}_{s}\rangle$
, where
$u_{s}^{\prime \prime }=u_{s}-\langle \overline{u}_{s}\rangle$
, where
![]() $\langle \overline{u}_{s}\rangle$
is the spatially averaged mean velocity in the
$\langle \overline{u}_{s}\rangle$
is the spatially averaged mean velocity in the
![]() $s$
direction. Hence, the associated spatially averaged Reynolds stresses can be expressed as
$s$
direction. Hence, the associated spatially averaged Reynolds stresses can be expressed as
![]() $\langle \overline{u_{i}^{\prime \prime }u_{j}^{\prime \prime }}\rangle$
using the operations defined in (3.3) and (3.4). Here
$\langle \overline{u_{i}^{\prime \prime }u_{j}^{\prime \prime }}\rangle$
using the operations defined in (3.3) and (3.4). Here
![]() $i,j=1,2,3$
for the streamwise, wall-normal and spanwise velocity components, respectively. The associated r.m.s. of turbulent–spatial velocity fluctuations is referred to as
$i,j=1,2,3$
for the streamwise, wall-normal and spanwise velocity components, respectively. The associated r.m.s. of turbulent–spatial velocity fluctuations is referred to as
![]() $u_{s,rms}^{\prime \prime }=\sqrt{\langle \overline{u_{s}^{\prime \prime }u_{s}^{\prime \prime }}\rangle }$
.
$u_{s,rms}^{\prime \prime }=\sqrt{\langle \overline{u_{s}^{\prime \prime }u_{s}^{\prime \prime }}\rangle }$
.
3.3. Detection of
 $y$
origin
$y$
origin
Following Breugem, Boersma & Uittenbogaard (Reference Breugem, Boersma and Uittenbogaard2006), the extent of the logarithmic layer is determined from a plot of a diagnostic function,
![]() ${\it\Xi}=y^{\prime +}(\text{d}\langle \overline{u}\rangle ^{+}/\text{d}y^{\prime +})$
, with respect to
${\it\Xi}=y^{\prime +}(\text{d}\langle \overline{u}\rangle ^{+}/\text{d}y^{\prime +})$
, with respect to
![]() $y^{\prime +}$
, where
$y^{\prime +}$
, where
![]() $y^{\prime +}=(y+{\it\varepsilon}_{d})^{+}$
. Here,
$y^{\prime +}=(y+{\it\varepsilon}_{d})^{+}$
. Here,
![]() $y$
is the distance measured from the roughness crest, and
$y$
is the distance measured from the roughness crest, and
![]() ${\it\varepsilon}_{d}$
is the distance by which the origin is shifted. In the region where the log law is satisfied, the value of the diagnostic function must be constant and equal to
${\it\varepsilon}_{d}$
is the distance by which the origin is shifted. In the region where the log law is satisfied, the value of the diagnostic function must be constant and equal to
![]() $1/{\it\kappa}$
, where
$1/{\it\kappa}$
, where
![]() ${\it\kappa}$
is the von Kármán constant. Hence, a flat plateau is expected for this region of the plot. A systematic procedure is adopted for determining the origin using this criterion. Figure 4(a) shows an example of such plots for PA7400 (with
${\it\kappa}$
is the von Kármán constant. Hence, a flat plateau is expected for this region of the plot. A systematic procedure is adopted for determining the origin using this criterion. Figure 4(a) shows an example of such plots for PA7400 (with
![]() ${\it\kappa}=0.41$
). The flat plateau can clearly be recognised for
${\it\kappa}=0.41$
). The flat plateau can clearly be recognised for
![]() ${\it\varepsilon}_{d}=0.03$
and
${\it\varepsilon}_{d}=0.03$
and
![]() $y^{\prime +}\in [50,90]$
. For the lower-Reynolds-number case, PA2800 (not shown), although the extent of the region is not very clear, it is valid for
$y^{\prime +}\in [50,90]$
. For the lower-Reynolds-number case, PA2800 (not shown), although the extent of the region is not very clear, it is valid for
![]() $y^{\prime +}\in [50,65]$
with the same shifting distance of
$y^{\prime +}\in [50,65]$
with the same shifting distance of
![]() ${\it\varepsilon}_{d}=0.03$
. Therefore, for all simulations presented herein, the origin of the ‘wall’ is considered to be
${\it\varepsilon}_{d}=0.03$
. Therefore, for all simulations presented herein, the origin of the ‘wall’ is considered to be
![]() ${\it\varepsilon}_{d}=0.03$
below the roughness crest, namely
${\it\varepsilon}_{d}=0.03$
below the roughness crest, namely
![]() $y^{\prime }=y+0.03$
. Both
$y^{\prime }=y+0.03$
. Both
![]() $y$
and
$y$
and
![]() $y^{\prime }$
are used in this paper. Figure 4(b) shows the variations of mean velocity profile using this shifting distance for PA7400.
$y^{\prime }$
are used in this paper. Figure 4(b) shows the variations of mean velocity profile using this shifting distance for PA7400.

Figure 5. Flow structures in isosurface plots at (a)
![]() $t^{\ast }=0.09$
, (b)
$t^{\ast }=0.09$
, (b)
![]() $t^{\ast }=0.2$
, (c)
$t^{\ast }=0.2$
, (c)
![]() $t^{\ast }=0.25$
, (d)
$t^{\ast }=0.25$
, (d)
![]() $t^{\ast }=0.4$
, (e)
$t^{\ast }=0.4$
, (e)
![]() $t^{\ast }=0.6$
, (f)
$t^{\ast }=0.6$
, (f)
![]() $t^{\ast }=0.8$
, (g)
$t^{\ast }=0.8$
, (g)
![]() $t^{\ast }=1.5$
and (h)
$t^{\ast }=1.5$
and (h)
![]() $t^{\ast }=4$
. Shown are 3D plots of low- and high-speed streaks and
$t^{\ast }=4$
. Shown are 3D plots of low- and high-speed streaks and
![]() ${\it\lambda}_{2}$
, coloured by blue (
${\it\lambda}_{2}$
, coloured by blue (
![]() $u^{\prime \prime }/u_{{\it\tau}0}=-10$
), green (
$u^{\prime \prime }/u_{{\it\tau}0}=-10$
), green (
![]() $u^{\prime \prime }/u_{{\it\tau}0}=+10$
) and red
$u^{\prime \prime }/u_{{\it\tau}0}=+10$
) and red
![]() $({\it\lambda}_{2}/(u_{{\it\tau}0}/{\it\delta})^{2}=-1.1)$
, respectively. For clarity, data are shown for part of the full-scale geometry (one quarter and one fifth in streamwise and spanwise directions, respectively).
$({\it\lambda}_{2}/(u_{{\it\tau}0}/{\it\delta})^{2}=-1.1)$
, respectively. For clarity, data are shown for part of the full-scale geometry (one quarter and one fifth in streamwise and spanwise directions, respectively).
4. Results
4.1. Flow visualisations and vortex structures during the transient
Figure 5 shows 3D isosurface plots of low- and high-speed streaks,
![]() $\mp u^{\prime \prime }=(u-\langle \overline{u}\rangle )$
, and negative
$\mp u^{\prime \prime }=(u-\langle \overline{u}\rangle )$
, and negative
![]() ${\it\lambda}_{2}$
at several instants of the transient flow. Note that, for the sake of clarity of the structures, only a quarter of the streamwise and a fifth of the spanwise extents of the simulated domain are shown. Here,
${\it\lambda}_{2}$
at several instants of the transient flow. Note that, for the sake of clarity of the structures, only a quarter of the streamwise and a fifth of the spanwise extents of the simulated domain are shown. Here,
![]() ${\it\lambda}_{2}$
is the second largest eigenvalue of the symmetric tensor
${\it\lambda}_{2}$
is the second largest eigenvalue of the symmetric tensor
![]() $\unicode[STIX]{x1D64E}^{2}+{\it\bf\Omega}^{2}$
, where
$\unicode[STIX]{x1D64E}^{2}+{\it\bf\Omega}^{2}$
, where
![]() $\unicode[STIX]{x1D64E}$
and
$\unicode[STIX]{x1D64E}$
and
![]() ${\it\bf\Omega}$
are the symmetric and antisymmetric parts of the velocity gradient tensor,
${\it\bf\Omega}$
are the symmetric and antisymmetric parts of the velocity gradient tensor,
![]() ${\rm\nabla}\unicode[STIX]{x1D66A}$
.
${\rm\nabla}\unicode[STIX]{x1D66A}$
.
The negative isosurface of
![]() ${\it\lambda}_{2}$
is used to identify vortex cores (Jeong & Hussain Reference Jeong and Hussain1995). Note that all visualised quantities are normalised by wall units of the initial flow. It is seen that, following the step increase in flow rate, the flow undergoes a distinctive transient phase. During this process, a well-organised roughness-induced, strong, head-up hairpin structure is initially generated around each roughness element. These vortices, which are similar to each other in both size and strength over all elements in the flow domain, are then convected downstream in the flow direction and evolve in the subsequent instants. In the following, the birth and development of such vortices over the roughness elements are explained.
${\it\lambda}_{2}$
is used to identify vortex cores (Jeong & Hussain Reference Jeong and Hussain1995). Note that all visualised quantities are normalised by wall units of the initial flow. It is seen that, following the step increase in flow rate, the flow undergoes a distinctive transient phase. During this process, a well-organised roughness-induced, strong, head-up hairpin structure is initially generated around each roughness element. These vortices, which are similar to each other in both size and strength over all elements in the flow domain, are then convected downstream in the flow direction and evolve in the subsequent instants. In the following, the birth and development of such vortices over the roughness elements are explained.
Referring to figure 5, soon after the commencement of the transient (
![]() $t^{\ast }=0.09$
), a region of strong vortex (shown by
$t^{\ast }=0.09$
), a region of strong vortex (shown by
![]() ${\it\lambda}_{2}$
isosurfaces) develops around the roughness crest extending along the spanwise ridge line. Later (
${\it\lambda}_{2}$
isosurfaces) develops around the roughness crest extending along the spanwise ridge line. Later (
![]() $t^{\ast }=0.2$
), the vortex is split into two parts. One part remains at the location of its birth (that is, at the crest of the roughness element) throughout the rest of the transient process (see later instants). The second part is convected downstream and plays a major role in the transition. The lower parts of this new vortex traverse alongside the two trough lines, and the upper necklace part located behind the roughness crest goes downstream along the ridge line. At
$t^{\ast }=0.2$
), the vortex is split into two parts. One part remains at the location of its birth (that is, at the crest of the roughness element) throughout the rest of the transient process (see later instants). The second part is convected downstream and plays a major role in the transition. The lower parts of this new vortex traverse alongside the two trough lines, and the upper necklace part located behind the roughness crest goes downstream along the ridge line. At
![]() $t^{\ast }=0.25$
, a typical primary hairpin vortex has emerged, with two counter-rotating legs alongside the ridge lines and the head in the roughness wake (around the trough). This vortex has travelled half of the roughness wavelength (
$t^{\ast }=0.25$
, a typical primary hairpin vortex has emerged, with two counter-rotating legs alongside the ridge lines and the head in the roughness wake (around the trough). This vortex has travelled half of the roughness wavelength (
![]() $x/{\it\lambda}=0.5$
) by this instant. At this stage, the vortices are still very close to the surface. By
$x/{\it\lambda}=0.5$
) by this instant. At this stage, the vortices are still very close to the surface. By
![]() $t^{\ast }\sim 0.4$
, the head of the quasi-streamwise primary vortex has reached the crest of the successive roughness element, and starts to move away from the wall.
$t^{\ast }\sim 0.4$
, the head of the quasi-streamwise primary vortex has reached the crest of the successive roughness element, and starts to move away from the wall.
Figure 6(a) shows a close-up view of the hairpin structures at this instant. It is also seen that the region of the strong hairpin vortices is associated with the low-pressure region. From approximately
![]() $t^{\ast }=0.8$
, a significant burst of the primary hairpins is observed and the vortices are replaced by more random and smaller vortical structures. By
$t^{\ast }=0.8$
, a significant burst of the primary hairpins is observed and the vortices are replaced by more random and smaller vortical structures. By
![]() $t^{\ast }\sim 4$
, there are no strong structures identified near the roughness and the flow in the roughness sublayer has effectively reached the final flow condition. This trend is consistent with the development of the turbulence quantities (e.g.
$t^{\ast }\sim 4$
, there are no strong structures identified near the roughness and the flow in the roughness sublayer has effectively reached the final flow condition. This trend is consistent with the development of the turbulence quantities (e.g.
![]() $U_{m}^{+}$
and
$U_{m}^{+}$
and
![]() $u^{\prime }v^{\prime }$
) discussed in the following sections, in which, by
$u^{\prime }v^{\prime }$
) discussed in the following sections, in which, by
![]() $t^{\ast }\sim 4$
, the inner layer (
$t^{\ast }\sim 4$
, the inner layer (
![]() $y^{\prime +}<100$
) has reached the final flow values.
$y^{\prime +}<100$
) has reached the final flow values.
The formation of streaks is another distinctive feature of the transition process. As shown in figure 5, at a very early stage (
![]() $t^{\ast }=0.25$
), positive streaks (green structures) are formed, which go along the troughs of the roughness elements. At this time, patches of negative velocity are formed within the primary vortices. At a later time (
$t^{\ast }=0.25$
), positive streaks (green structures) are formed, which go along the troughs of the roughness elements. At this time, patches of negative velocity are formed within the primary vortices. At a later time (
![]() $t^{\ast }=0.4$
), the negative velocity streaks are formed as such patches are connected. This is also the time when the heads of the primary vortices move away from the wall (see side-view plots of figure 6
b–g). This creates a situation where all the primary vortices sit on top of the negative streaks, which is a typical scenario identified in bypass transition (Jacobs & Durbin Reference Jacobs and Durbin2001; Nolan, Walsh & Mceligot Reference Nolan, Walsh and Mceligot2010). In fact the positive and negative streaks are themselves supporting evidence of the existence of a strong counter-rotating vortex (Alfonsi Reference Alfonsi2006). Note that for figure 5 an isosurface level that better depicts the streaky structures during the transient flow was chosen and applied to all instants; as a consequence, the streaky structures at
$t^{\ast }=0.4$
), the negative velocity streaks are formed as such patches are connected. This is also the time when the heads of the primary vortices move away from the wall (see side-view plots of figure 6
b–g). This creates a situation where all the primary vortices sit on top of the negative streaks, which is a typical scenario identified in bypass transition (Jacobs & Durbin Reference Jacobs and Durbin2001; Nolan, Walsh & Mceligot Reference Nolan, Walsh and Mceligot2010). In fact the positive and negative streaks are themselves supporting evidence of the existence of a strong counter-rotating vortex (Alfonsi Reference Alfonsi2006). Note that for figure 5 an isosurface level that better depicts the streaky structures during the transient flow was chosen and applied to all instants; as a consequence, the streaky structures at
![]() $t^{\ast }=0.09$
, which exist due to initial turbulence, are not visible.
$t^{\ast }=0.09$
, which exist due to initial turbulence, are not visible.

Figure 6. Primary vortex structure and pressure. (a) Close-up view of vortex structure (
![]() $-{\it\lambda}_{2}$
) and negative pressure at
$-{\it\lambda}_{2}$
) and negative pressure at
![]() $t^{\ast }=0.4$
. (b–g) Isosurface of
$t^{\ast }=0.4$
. (b–g) Isosurface of
![]() ${\it\lambda}_{2}$
of figure 5 shown in side view (
${\it\lambda}_{2}$
of figure 5 shown in side view (
![]() $x$
–
$x$
–
![]() $y$
plane): (b)
$y$
plane): (b)
![]() $t^{\ast }=0.09$
, (c)
$t^{\ast }=0.09$
, (c)
![]() $t^{\ast }=0.25$
, (d)
$t^{\ast }=0.25$
, (d)
![]() $t^{\ast }=0.42$
, (e)
$t^{\ast }=0.42$
, (e)
![]() $t^{\ast }=0.6$
, (f)
$t^{\ast }=0.6$
, (f)
![]() $t^{\ast }=0.8$
and (g)
$t^{\ast }=0.8$
and (g)
![]() $t^{\ast }=4$
. For clarity, the side-view plots are shown for half a roughness spanwise wavelength. The dashed lines in the side-view plots show the location of
$t^{\ast }=4$
. For clarity, the side-view plots are shown for half a roughness spanwise wavelength. The dashed lines in the side-view plots show the location of
![]() $y/k_{t}=3$
.
$y/k_{t}=3$
.
The existence of standing and hairpin vortices, and the evolution and breakdown of the latter in the transient flow, bears a strong qualitative resemblance to those of the roughness-induced laminar–turbulent transition described by Acarlar & Smith (Reference Acarlar and Smith1987) for a low-speed Blasius boundary layer and by De Tullio et al. (Reference De Tullio, Paredes, Sandham and Theofilis2013) for a supersonic boundary layer for an isolated roughness element. This is particularly interesting considering that, in the present case, (i) the initial flow is a turbulent flow in the transitionally rough regime (
![]() $k_{s}^{+}\sim 15$
), and (ii) the transient process occurs over a surface that is entirely covered by close-packed distributed roughness elements in both the streamwise and spanwise directions. It is shown later (e.g. refer to figure 9
c) that, in the transient flow considered herein, a boundary layer is formed as a result of the rapid increase of Reynolds number. This creates a condition similar to that in a spatially developing boundary layer, resulting in the generation of vortices and later their breakdown.
$k_{s}^{+}\sim 15$
), and (ii) the transient process occurs over a surface that is entirely covered by close-packed distributed roughness elements in both the streamwise and spanwise directions. It is shown later (e.g. refer to figure 9
c) that, in the transient flow considered herein, a boundary layer is formed as a result of the rapid increase of Reynolds number. This creates a condition similar to that in a spatially developing boundary layer, resulting in the generation of vortices and later their breakdown.

Figure 7. Vector plot and contour of
![]() ${\it\lambda}_{2}$
(negative values are shaded) at
${\it\lambda}_{2}$
(negative values are shaded) at
![]() $x/{\it\delta}=1.503$
(
$x/{\it\delta}=1.503$
(
![]() $x/{\it\lambda}=0.005$
).
$x/{\it\lambda}=0.005$
).
To investigate further the generation and evolution of the strong primary hairpin vortices during the early stage of the transient process, the development of the velocity fields (
![]() $v,w$
) at several instants is shown in figure 7 in the form of vector plots in a vertical
$v,w$
) at several instants is shown in figure 7 in the form of vector plots in a vertical
![]() $y$
–
$y$
–
![]() $z$
plane across two roughness elements. The plane is chosen at
$z$
plane across two roughness elements. The plane is chosen at
![]() $x/{\it\delta}=1.503$
(
$x/{\it\delta}=1.503$
(
![]() $x/{\it\lambda}=0.005$
), which is very close to the crest of the forward side of the element. The vector frames are shaded with contours of the negative
$x/{\it\lambda}=0.005$
), which is very close to the crest of the forward side of the element. The vector frames are shaded with contours of the negative
![]() ${\it\lambda}_{2}$
, which is normalised by
${\it\lambda}_{2}$
, which is normalised by
![]() $(u_{{\it\tau}_{0}}/{\it\delta})^{2}$
. Very shortly after the commencement of the transient (
$(u_{{\it\tau}_{0}}/{\it\delta})^{2}$
. Very shortly after the commencement of the transient (
![]() $t^{\ast }=0.09$
), upward activities (although relatively weak) are observed to occupy much of the surface of the roughness, which can be identified from the velocity vectors. The second frame (
$t^{\ast }=0.09$
), upward activities (although relatively weak) are observed to occupy much of the surface of the roughness, which can be identified from the velocity vectors. The second frame (
![]() $t^{\ast }=0.3$
) corresponds to an instant close to when the primary hairpin structures are formed. It can be seen from the velocity vectors and the strong negative values of
$t^{\ast }=0.3$
) corresponds to an instant close to when the primary hairpin structures are formed. It can be seen from the velocity vectors and the strong negative values of
![]() ${\it\lambda}_{2}$
that a pair of counter-rotating vortices is present within each trough. These are signatures of the hairpin legs. The vortices are centred in a low-speed streak and are surrounded by high-speed streaks (not shown here). At
${\it\lambda}_{2}$
that a pair of counter-rotating vortices is present within each trough. These are signatures of the hairpin legs. The vortices are centred in a low-speed streak and are surrounded by high-speed streaks (not shown here). At
![]() $t^{\ast }=0.5$
, the signature of a hairpin head can be observed just above the trough. Here the velocity vectors go outwards at an elevated level and the low-speed streak starts to lift from the wall. The fourth frame (
$t^{\ast }=0.5$
, the signature of a hairpin head can be observed just above the trough. Here the velocity vectors go outwards at an elevated level and the low-speed streak starts to lift from the wall. The fourth frame (
![]() $t^{\ast }=0.8$
) shows the vectors for the time when the breakdown of the organised hairpins has been started, and at
$t^{\ast }=0.8$
) shows the vectors for the time when the breakdown of the organised hairpins has been started, and at
![]() $t^{\ast }=1.5$
(fifth frame) most such structures near the roughness have already been pumped and broken up. At a later time (
$t^{\ast }=1.5$
(fifth frame) most such structures near the roughness have already been pumped and broken up. At a later time (
![]() $t^{\ast }\sim 4$
) the organised structures near the roughness have completely disappeared.
$t^{\ast }\sim 4$
) the organised structures near the roughness have completely disappeared.
It is useful to note that, during the first stage (
![]() $t^{\ast }<0.8$
), signatures of the primary hairpin’s heads and legs (exhibited in figure 7 as strong vortical structures) are confined up to
$t^{\ast }<0.8$
), signatures of the primary hairpin’s heads and legs (exhibited in figure 7 as strong vortical structures) are confined up to
![]() $y/k_{t}\sim 3$
above the roughness crest. This is also confirmed by the development of energy spectra discussed in § 4.6, where the strong spikes exhibited at the wavenumbers corresponding to the roughness wavelength and its multiples largely vanish for locations above
$y/k_{t}\sim 3$
above the roughness crest. This is also confirmed by the development of energy spectra discussed in § 4.6, where the strong spikes exhibited at the wavenumbers corresponding to the roughness wavelength and its multiples largely vanish for locations above
![]() $y/k_{t}\sim 3$
. In studies for which the flow field is available (e.g. using DNS or particle image velocimetry), the height of the roughness sublayer is normally defined as the distance at which the spatial variation of Reynolds stresses is diminished (Bhaganagar, Kim & Coleman Reference Bhaganagar, Kim and Coleman2004; Hong et al.
Reference Hong, Katz and Schultz2011; Lee, Sung & Krogstad Reference Lee, Sung and Krogstad2011). This sublayer has been found to be 2–5 times the roughness height. Another definition of the roughness sublayer thickness used in the literature is the distance beyond which the statistical values of rough and smooth wall start to collapse (Bakken et al.
Reference Bakken, Krogstad, Ashrafian and Andersson2005; Schultz & Flack Reference Schultz and Flack2005). Following the above methods, the present steady-flow results show that, for both the low- and high-Reynolds-number cases, the roughness sublayer is approximately
$y/k_{t}\sim 3$
. In studies for which the flow field is available (e.g. using DNS or particle image velocimetry), the height of the roughness sublayer is normally defined as the distance at which the spatial variation of Reynolds stresses is diminished (Bhaganagar, Kim & Coleman Reference Bhaganagar, Kim and Coleman2004; Hong et al.
Reference Hong, Katz and Schultz2011; Lee, Sung & Krogstad Reference Lee, Sung and Krogstad2011). This sublayer has been found to be 2–5 times the roughness height. Another definition of the roughness sublayer thickness used in the literature is the distance beyond which the statistical values of rough and smooth wall start to collapse (Bakken et al.
Reference Bakken, Krogstad, Ashrafian and Andersson2005; Schultz & Flack Reference Schultz and Flack2005). Following the above methods, the present steady-flow results show that, for both the low- and high-Reynolds-number cases, the roughness sublayer is approximately
![]() $y\sim 3k_{t}$
above the crest.
$y\sim 3k_{t}$
above the crest.
Overall, the observations from figures 5 to 7 demonstrate that the transient process following the step increase of flow rate is characterised by a rather orderly process of one cycle of the birth of uniformly distributed quasi-streamwise primary hairpin vortices, followed by the evolution and eventual breakdown of these vortices. The number of such hairpin vortices is equal to the number of roughness elements. At a very early stage (say around
![]() $t^{\ast }=0.1$
), a vortex is formed on the crest of each of the roughness elements, and it later splits into two (
$t^{\ast }=0.1$
), a vortex is formed on the crest of each of the roughness elements, and it later splits into two (
![]() $t^{\ast }=0.2$
): a ‘standing’ vortex, which remains locally and largely inactive during later development, and a ‘primary hairpin’, which is convected downstream and forms a primary hairpin vortex with two counter-rotating legs joining at the head, at (
$t^{\ast }=0.2$
): a ‘standing’ vortex, which remains locally and largely inactive during later development, and a ‘primary hairpin’, which is convected downstream and forms a primary hairpin vortex with two counter-rotating legs joining at the head, at (
![]() $t^{\ast }\sim 0.25$
). Later, the primary vortices are convected downstream and their heads move away from the wall. Alongside this, two sets of streaks are generated within the span of every roughness element. The low-speed streaks sit below the hairpin vortices, which are accompanied by strong ejection activities. At
$t^{\ast }\sim 0.25$
). Later, the primary vortices are convected downstream and their heads move away from the wall. Alongside this, two sets of streaks are generated within the span of every roughness element. The low-speed streaks sit below the hairpin vortices, which are accompanied by strong ejection activities. At
![]() $t^{\ast }\sim 0.8$
, a significant breakup of the vortices has started and eventually the orderly vortical structures are replaced by more chaotic structures that are typical of turbulent flows over a rough wall. It will take some time for the newly generated turbulence to propagate to the core of the flow, as will be demonstrated later.
$t^{\ast }\sim 0.8$
, a significant breakup of the vortices has started and eventually the orderly vortical structures are replaced by more chaotic structures that are typical of turbulent flows over a rough wall. It will take some time for the newly generated turbulence to propagate to the core of the flow, as will be demonstrated later.
4.2. Skin friction factor
The skin friction factor coefficient,
![]() $C_{f}$
, is defined as
$C_{f}$
, is defined as
where
![]() ${\it\tau}_{w}$
is the wall shear stress, denoted by
${\it\tau}_{w}$
is the wall shear stress, denoted by
![]() ${\it\tau}_{ws}$
and
${\it\tau}_{ws}$
and
![]() ${\it\tau}_{wr}$
for the upper (smooth) and lower (rough) walls, respectively. For the smooth wall, the calculation of
${\it\tau}_{wr}$
for the upper (smooth) and lower (rough) walls, respectively. For the smooth wall, the calculation of
![]() ${\it\tau}_{ws}$
is straightforward and can be obtained from the mean velocity profile,
${\it\tau}_{ws}$
is straightforward and can be obtained from the mean velocity profile,
For the rough wall, shear stress contains the contribution of both pressure drag (
![]() $P_{d}$
) and friction drag (
$P_{d}$
) and friction drag (
![]() ${\it\tau}_{f}$
), and is calculated using
${\it\tau}_{f}$
), and is calculated using
![]() ${\it\tau}_{ws}$
and the mean pressure gradient of the channel (
${\it\tau}_{ws}$
and the mean pressure gradient of the channel (
![]() ${\it\Pi}$
in (2.1)) via the expression (Seddighi Reference Seddighi2011)
${\it\Pi}$
in (2.1)) via the expression (Seddighi Reference Seddighi2011)
where
![]() $S_{e}$
is the total flow area. In fact, it is the total area minus that associated with the roughness elements; so for the smooth case it is
$S_{e}$
is the total flow area. In fact, it is the total area minus that associated with the roughness elements; so for the smooth case it is
![]() $S_{e}=(2{\it\delta})L_{x}$
. For the rough case, the height of the channel (
$S_{e}=(2{\it\delta})L_{x}$
. For the rough case, the height of the channel (
![]() $2{\it\delta}$
) varies slightly due to the roughness and an average is used. Leonardi, Orlandi & Antonia (Reference Leonardi, Orlandi and Antonia2005) proposed a method that is similarly based on the global momentum balance formula for the total pressure drop. The wall shear stress for each wall is determined from the total pressure loss and the zero-crossing in the wall-normal profile of the turbulent shear stress:
$2{\it\delta}$
) varies slightly due to the roughness and an average is used. Leonardi, Orlandi & Antonia (Reference Leonardi, Orlandi and Antonia2005) proposed a method that is similarly based on the global momentum balance formula for the total pressure drop. The wall shear stress for each wall is determined from the total pressure loss and the zero-crossing in the wall-normal profile of the turbulent shear stress:
where
![]() $d_{1}$
and
$d_{1}$
and
![]() $d_{2}$
are the distances of the zero-crossing from the upper and lower wall, respectively. For the present results, both methods are used and are found to give similar values with a difference of less than 1 %. Friction factors for the top smooth wall obtained for the steady-state rough-case simulations are in close agreement with those from the literature (Monty Reference Monty2005).
$d_{2}$
are the distances of the zero-crossing from the upper and lower wall, respectively. For the present results, both methods are used and are found to give similar values with a difference of less than 1 %. Friction factors for the top smooth wall obtained for the steady-state rough-case simulations are in close agreement with those from the literature (Monty Reference Monty2005).
Figure 8 shows the development of the friction coefficient for the transient flow. Also shown are the results of HS2013 for a channel with all smooth walls (smooth case). It is seen that the development of the friction coefficient for the smooth wall is consistent with the results of HS2013, exhibiting a bypass transition behaviour as discussed in § 1. A large undershoot, until
![]() $t^{\ast }\sim 8$
, exhibited by the smooth wall is characteristic of the flow in the pre-transition stage during which the flow exhibits a trend of a laminar friction factor (He & Seddighi Reference He and Seddighi2015). The friction factor for the rough wall, however, shows a trend that is significantly different from that of the smooth wall. The development shows neither a large undershoot at the initial stages, nor a long delay (until
$t^{\ast }\sim 8$
, exhibited by the smooth wall is characteristic of the flow in the pre-transition stage during which the flow exhibits a trend of a laminar friction factor (He & Seddighi Reference He and Seddighi2015). The friction factor for the rough wall, however, shows a trend that is significantly different from that of the smooth wall. The development shows neither a large undershoot at the initial stages, nor a long delay (until
![]() $t^{\ast }\sim 16$
) before reaching the corresponding final flow value. This behaviour is not a surprise, noting that strong hairpin vortices are generated very early in time (
$t^{\ast }\sim 16$
) before reaching the corresponding final flow value. This behaviour is not a surprise, noting that strong hairpin vortices are generated very early in time (
![]() $t^{\ast }\sim 0.25$
), and the transition is already completed by
$t^{\ast }\sim 0.25$
), and the transition is already completed by
![]() $t^{\ast }\sim 4$
. The variation of
$t^{\ast }\sim 4$
. The variation of
![]() $C_{f}$
is largely dominated by the relaxation of the mean velocity profile, which causes a continual reduction from its initial peak value resulting from the sudden increase in flow rate. The effect of the primary vortex generated at
$C_{f}$
is largely dominated by the relaxation of the mean velocity profile, which causes a continual reduction from its initial peak value resulting from the sudden increase in flow rate. The effect of the primary vortex generated at
![]() $t^{\ast }\sim 0.25$
is reflected as a kink in the variation of
$t^{\ast }\sim 0.25$
is reflected as a kink in the variation of
![]() $C_{f}$
(see the inset). In the period of
$C_{f}$
(see the inset). In the period of
![]() $0.25<t^{\ast }<0.8$
, the profile shows an oscillatory variation with several further kinks. The period corresponds to the time during which the primary vortices are pumping up from the wall, whilst convecting downstream of the flow. The vortices remain in
$0.25<t^{\ast }<0.8$
, the profile shows an oscillatory variation with several further kinks. The period corresponds to the time during which the primary vortices are pumping up from the wall, whilst convecting downstream of the flow. The vortices remain in
![]() $y/k_{t}<1$
until
$y/k_{t}<1$
until
![]() $t^{\ast }\sim 0.8$
, when the major breakup of the primary vortices has started to occur. It is of particular interest to note that, in contrast to the development of the transient flow over a smooth wall in the corresponding period, the
$t^{\ast }\sim 0.8$
, when the major breakup of the primary vortices has started to occur. It is of particular interest to note that, in contrast to the development of the transient flow over a smooth wall in the corresponding period, the
![]() $C_{f}$
–
$C_{f}$
–
![]() $t^{\ast }$
curve for the rough wall is convex during the early transition period (
$t^{\ast }$
curve for the rough wall is convex during the early transition period (
![]() $t^{\ast }\sim 1.5$
). This reflects the fact that the flow during this period is not a simple diffusion process (as in a laminar flow), but is also affected by the generation and evolution of vortices, thereby causing a change in effective diffusivity and a higher friction coefficient.
$t^{\ast }\sim 1.5$
). This reflects the fact that the flow during this period is not a simple diffusion process (as in a laminar flow), but is also affected by the generation and evolution of vortices, thereby causing a change in effective diffusivity and a higher friction coefficient.

Figure 8. Development of the skin friction coefficient,
![]() $C_{f}$
, for the unsteady case; symbols show the smooth-wall results of He & Seddighi (Reference He and Seddighi2013).
$C_{f}$
, for the unsteady case; symbols show the smooth-wall results of He & Seddighi (Reference He and Seddighi2013).

Figure 9. Development of mean velocity profiles at several instants: (a) smooth wall; (b) rough wall. (c) Plot of
![]() $\overline{u}^{\wedge }$
(the profiles are shifted by an amount proportional to the time instant): thin lines, smooth wall; thick lines, rough wall. Lines 1 and 2 show the thickness of the boundary layer of
$\overline{u}^{\wedge }$
(the profiles are shifted by an amount proportional to the time instant): thin lines, smooth wall; thick lines, rough wall. Lines 1 and 2 show the thickness of the boundary layer of
![]() $\overline{u}^{\wedge }$
,
$\overline{u}^{\wedge }$
,
![]() ${\it\delta}_{99}$
, for the rough and smooth walls, respectively. The crest’s level is shown by the short-dashed line. (d) Plot of contour lines of mean velocity
${\it\delta}_{99}$
, for the rough and smooth walls, respectively. The crest’s level is shown by the short-dashed line. (d) Plot of contour lines of mean velocity
![]() $\overline{u}$
, shaded by
$\overline{u}$
, shaded by
![]() $\overline{u^{\prime }v^{\prime }}/u_{{\it\tau}0}^{2}$
, for the
$\overline{u^{\prime }v^{\prime }}/u_{{\it\tau}0}^{2}$
, for the
![]() $y$
–
$y$
–
![]() $z$
plane at
$z$
plane at
![]() $x/{\it\lambda}=0$
and
$x/{\it\lambda}=0$
and
![]() $t^{\ast }=0.8$
.
$t^{\ast }=0.8$
.
4.3. Mean velocity, r.m.s. of velocity fluctuations
Figure 9 shows the mean velocity profiles for the unsteady flow at several instants. The velocity and effective distance, normalised by inner scaling, are shown in figure 9(a,b) for the smooth- and rough-wall cases, respectively. The development for the smooth wall shows a trend similar to that of the all-smooth channel of HS2013. After an initial reduction (
![]() $t^{\ast }<0.02$
), the velocity (
$t^{\ast }<0.02$
), the velocity (
![]() $\langle \overline{u}\rangle ^{+}$
) increases monotonically until the onset of transition (
$\langle \overline{u}\rangle ^{+}$
) increases monotonically until the onset of transition (
![]() $t^{\ast }\sim 8$
). During this period, the extent of the viscous sublayer (approximated by
$t^{\ast }\sim 8$
). During this period, the extent of the viscous sublayer (approximated by
![]() $\langle \overline{u}\rangle ^{+}=y^{\prime +}$
) increases with time. After the transition begins, the velocity in the core region progressively reduces, reaching a profile close to that in a steady flow at the end of the transition (
$\langle \overline{u}\rangle ^{+}=y^{\prime +}$
) increases with time. After the transition begins, the velocity in the core region progressively reduces, reaching a profile close to that in a steady flow at the end of the transition (
![]() $t^{\ast }\sim 16$
). Later, whilst the profile in the inner region (
$t^{\ast }\sim 16$
). Later, whilst the profile in the inner region (
![]() ${\sim}y^{\prime +}<100$
) remains unchanged, the velocity in the wake region (
${\sim}y^{\prime +}<100$
) remains unchanged, the velocity in the wake region (
![]() ${\sim}y^{\prime +}>100$
) adjusts itself slightly to reach the corresponding final steady values. The velocity over the rough wall, however, evolves in a different manner. After the initial rapid reduction, the values increase monotonically until
${\sim}y^{\prime +}>100$
) adjusts itself slightly to reach the corresponding final steady values. The velocity over the rough wall, however, evolves in a different manner. After the initial rapid reduction, the values increase monotonically until
![]() $t^{\ast }\sim 4$
. By this time, the inner layer (
$t^{\ast }\sim 4$
. By this time, the inner layer (
![]() ${\sim}y^{\prime +}<100$
) reaches its final profile, remaining almost unchanged thereafter. As discussed in § 4.2 (figure 8), by
${\sim}y^{\prime +}<100$
) reaches its final profile, remaining almost unchanged thereafter. As discussed in § 4.2 (figure 8), by
![]() $t^{\ast }\sim 4$
, the friction factor has almost reached the value corresponding to the final flow. In the outer layer (
$t^{\ast }\sim 4$
, the friction factor has almost reached the value corresponding to the final flow. In the outer layer (
![]() $y^{\prime +}>100$
), the velocity continues to adjust while oscillating around the final profile until approximately
$y^{\prime +}>100$
), the velocity continues to adjust while oscillating around the final profile until approximately
![]() $t^{\ast }=16$
. Interestingly, the above trend of velocity development is similar to that reported by De Tullio et al. (Reference De Tullio, Paredes, Sandham and Theofilis2013, figure 18b) in the wake of an isolated roughness in a supersonic boundary layer where laminar–turbulent transition occurs.
$t^{\ast }=16$
. Interestingly, the above trend of velocity development is similar to that reported by De Tullio et al. (Reference De Tullio, Paredes, Sandham and Theofilis2013, figure 18b) in the wake of an isolated roughness in a supersonic boundary layer where laminar–turbulent transition occurs.
Following HS2013, the time-developing boundary layer can be studied by examining the perturbation velocity,
where
![]() $y^{\prime }=y+{\it\epsilon}_{d}$
for the rough wall and
$y^{\prime }=y+{\it\epsilon}_{d}$
for the rough wall and
![]() $y^{\prime }$
is the wall-normal distance from the top wall for the smooth wall; and
$y^{\prime }$
is the wall-normal distance from the top wall for the smooth wall; and
![]() $\langle \overline{u}_{c}\rangle$
is the mean velocity corresponding to the effective centreline for each wall. Figure 9(c) shows such profiles against elevation of
$\langle \overline{u}_{c}\rangle$
is the mean velocity corresponding to the effective centreline for each wall. Figure 9(c) shows such profiles against elevation of
![]() $y^{\prime }$
. For the smooth wall, the perturbation velocity profile is initially uniform along the
$y^{\prime }$
. For the smooth wall, the perturbation velocity profile is initially uniform along the
![]() $y^{\prime }$
axis, exhibiting a ‘plug-flow’ behaviour except in the vicinity of the wall, where a thin boundary layer is formed due to the ‘no-slip’ boundary condition on the wall. The boundary layer gradually develops into the core of the flow with time. The
$y^{\prime }$
axis, exhibiting a ‘plug-flow’ behaviour except in the vicinity of the wall, where a thin boundary layer is formed due to the ‘no-slip’ boundary condition on the wall. The boundary layer gradually develops into the core of the flow with time. The
![]() $\overline{u}^{\wedge }$
profiles at the various time instants are practically indistinguishable from those in the corresponding flow in a wholly smooth-wall channel of He & Seddighi (Reference He and Seddighi2015), which in turn agrees closely with the Stokes solution for a laminar flow during the pre-transition period (
$\overline{u}^{\wedge }$
profiles at the various time instants are practically indistinguishable from those in the corresponding flow in a wholly smooth-wall channel of He & Seddighi (Reference He and Seddighi2015), which in turn agrees closely with the Stokes solution for a laminar flow during the pre-transition period (
![]() $t^{\ast }<8$
). The latter two data are not shown to avoid over-crowding the figure.
$t^{\ast }<8$
). The latter two data are not shown to avoid over-crowding the figure.
On the rough wall, initially (say,
![]() $t^{\ast }<0.25$
), the flow above the roughness elements again responds like a ‘plug flow’, i.e. the perturbation flow
$t^{\ast }<0.25$
), the flow above the roughness elements again responds like a ‘plug flow’, i.e. the perturbation flow
![]() $\overline{u}^{\wedge }$
is uniform along the
$\overline{u}^{\wedge }$
is uniform along the
![]() $y^{\prime }$
axis. The mean velocity within the roughness varies linearly from the value above the element height to zero at the bottom of the roughness elements. During this period (
$y^{\prime }$
axis. The mean velocity within the roughness varies linearly from the value above the element height to zero at the bottom of the roughness elements. During this period (
![]() $t^{\ast }<0.25$
), the turbulent stresses (
$t^{\ast }<0.25$
), the turbulent stresses (
![]() $u_{rms}^{\prime },v_{rms}^{\prime },w_{rms}^{\prime }$
) above the roughness crest remain largely unchanged (thin lines with symbols in the insets of figure 10
g,i,k). Consequently, at this stage, the flow above the roughness can be viewed as comprising the initial turbulent flow plus a ‘plug flow’ (i.e. the perturbation flow), the latter of which contains only a mean velocity with no fluctuating components. During the next period (
$u_{rms}^{\prime },v_{rms}^{\prime },w_{rms}^{\prime }$
) above the roughness crest remain largely unchanged (thin lines with symbols in the insets of figure 10
g,i,k). Consequently, at this stage, the flow above the roughness can be viewed as comprising the initial turbulent flow plus a ‘plug flow’ (i.e. the perturbation flow), the latter of which contains only a mean velocity with no fluctuating components. During the next period (
![]() $0.25<t^{\ast }<0.8$
), the boundary layer that is initially confined within the roughness develops into the core at a rate that is significantly faster than that of the boundary layer over the smooth wall (see the development of the
$0.25<t^{\ast }<0.8$
), the boundary layer that is initially confined within the roughness develops into the core at a rate that is significantly faster than that of the boundary layer over the smooth wall (see the development of the
![]() ${\it\delta}_{99}$
profiles in figure 9
c). This period coincides with the growths and lift-ups of the hairpin vortices from the wall. The boundary layer continues developing after
${\it\delta}_{99}$
profiles in figure 9
c). This period coincides with the growths and lift-ups of the hairpin vortices from the wall. The boundary layer continues developing after
![]() $t^{\ast }=0.8$
, but, interestingly, a plateau develops in the profile just above the crest of the roughness elements. This coincides with the breakdown of primary vortices into conventional turbulence in the same region, which clearly provides strong mixing, leading to a flat velocity profile in that region. A similar behaviour was shown with the results of Acarlar & Smith (Reference Acarlar and Smith1987) and Muppidi & Mahesh (Reference Muppidi and Mahesh2012) for roughness-induced transition over, respectively, isolated and distributed roughness.
$t^{\ast }=0.8$
, but, interestingly, a plateau develops in the profile just above the crest of the roughness elements. This coincides with the breakdown of primary vortices into conventional turbulence in the same region, which clearly provides strong mixing, leading to a flat velocity profile in that region. A similar behaviour was shown with the results of Acarlar & Smith (Reference Acarlar and Smith1987) and Muppidi & Mahesh (Reference Muppidi and Mahesh2012) for roughness-induced transition over, respectively, isolated and distributed roughness.
The perturbation boundary layer can, in principle, be seen as an internal boundary layer (IBL) developing within the initial wall shear flow in the channel. In this regard, it is noted that the concept of IBLs developing within an external boundary layer has been studied extensively and particularly in the context of meteorology (e.g. Smits & Wood Reference Smits and Wood1985; Garratt Reference Garratt1990; Saito & Pullin Reference Saito and Pullin2014). The IBLs often result from a discontinuity in surface roughness (smooth to rough or vice versa) or surface temperature, with the free-stream velocity remaining unchanged. The perturbation introduced due to such a discontinuity is likely to be much milder than the sudden large increase in the mean velocity concerned here. In addition, previous research in the literature seems to focus on the steady development of the IBL after the initial transition, when the boundary layer growth indicates a turbulent power-law behaviour. In contrast, our main interest is the initial transition. Consequently, direct comparison with IBL results from the literature is not attempted herein.
Figure 9(d) shows the line contour plot of ensemble-averaged mean velocity
![]() $\overline{u}$
for the
$\overline{u}$
for the
![]() $y$
–
$y$
–
![]() $z$
plane at
$z$
plane at
![]() $x/{\it\lambda}=0$
, at
$x/{\it\lambda}=0$
, at
![]() $t^{\ast }=0.8$
. The plot is shaded by
$t^{\ast }=0.8$
. The plot is shaded by
![]() $\overline{u^{\prime }v^{\prime }}$
defined in § 4.4. A clear hump is seen for the contour line of the mean velocity in the region of the strong turbulent shear stress, which coincides with where the hairpin vortices exist. This behaviour is also similar to that of Drews et al. (Reference Drews, Downs, Doolittle, Goldstein and White2011) for the roughness-induced transition behind the roughness. The authors attributed the hump to the strong shear layer due to the existence of the hairpin vortices.
$\overline{u^{\prime }v^{\prime }}$
defined in § 4.4. A clear hump is seen for the contour line of the mean velocity in the region of the strong turbulent shear stress, which coincides with where the hairpin vortices exist. This behaviour is also similar to that of Drews et al. (Reference Drews, Downs, Doolittle, Goldstein and White2011) for the roughness-induced transition behind the roughness. The authors attributed the hump to the strong shear layer due to the existence of the hairpin vortices.

Figure 10. Development of r.m.s. of fluctuating velocities for smooth wall (a–f) and rough wall (g–l) at several locations: (a,c,e,g,i,k), near wall; (b,d,f,h,j,l), core region.
Figure 10 shows the development of r.m.s. of velocity fluctuations normalised by the initial friction velocity (
![]() $u_{{\it\tau}_{0}}$
), at several near-wall and core-region locations. Results for the smooth wall shown in figure 10(a–f) exhibit a bypass transition behaviour. In the wall region (figure 10
a,c,e),
$u_{{\it\tau}_{0}}$
), at several near-wall and core-region locations. Results for the smooth wall shown in figure 10(a–f) exhibit a bypass transition behaviour. In the wall region (figure 10
a,c,e),
![]() $w_{rms}^{\prime }$
are almost unchanged and even reduce slightly during pre-transition (
$w_{rms}^{\prime }$
are almost unchanged and even reduce slightly during pre-transition (
![]() $t^{\ast }\lesssim 8$
). In contrast, the streamwise component increases progressively owing to the formation of streaks (HS2013). During the transition,
$t^{\ast }\lesssim 8$
). In contrast, the streamwise component increases progressively owing to the formation of streaks (HS2013). During the transition,
![]() $u_{rms}^{\prime }$
continues to increase, reaching a maximum, from which it reduces and approaches final steady values towards the end of transition (
$u_{rms}^{\prime }$
continues to increase, reaching a maximum, from which it reduces and approaches final steady values towards the end of transition (
![]() $t^{\ast }\lesssim 16$
). Meanwhile, the other two components,
$t^{\ast }\lesssim 16$
). Meanwhile, the other two components,
![]() $v_{rms}^{\prime }$
and
$v_{rms}^{\prime }$
and
![]() $w_{rms}^{\prime }$
, increase monotonically, reaching the corresponding final steady values towards the end of transition. In the core region (figure 10
b,d,f), there are long delays in the responses of all three components. Data for the smooth case of HS2013 are shown (by the symbols) in figure 10(a–f) for direct comparison with the results for the smooth wall from the present study (shown by the lines). It can be seen that there is good agreement between the results of HS2013 and those for the smooth wall of the present simulation. In particular, the energy growth during the pre-transition period and the point of onset of transition are very close in the two cases.
$w_{rms}^{\prime }$
, increase monotonically, reaching the corresponding final steady values towards the end of transition. In the core region (figure 10
b,d,f), there are long delays in the responses of all three components. Data for the smooth case of HS2013 are shown (by the symbols) in figure 10(a–f) for direct comparison with the results for the smooth wall from the present study (shown by the lines). It can be seen that there is good agreement between the results of HS2013 and those for the smooth wall of the present simulation. In particular, the energy growth during the pre-transition period and the point of onset of transition are very close in the two cases.
This indicates that the flow over one wall of the channel, whether it is smooth or rough, has little influence on the transient flow behaviour on the opposite wall. That is, the local flows over the two sides of the channel are largely independent. This is in contrast to the results of Orlandi (Reference Orlandi2009) on laminar–turbulent transition, which showed that the transition is affected by the presence of the roughness on the opposite wall. Orlandi’s observation is not difficult to understand. The early transition on the rough surface, which generates strong and violent velocity and pressure fluctuations, can potentially induce earlier transition on the smooth wall. The turbulence generated near the rough wall will propagate towards the smooth wall, and hence increase the free-stream turbulence, which could in turn cause an early transition on the smooth wall. However, from figure 11 it is seen that the new turbulence resulting from the early transition over the rough surface, in the present study, is initially confined to the region close to the wall. It propagates relatively slowly to the core of the flow. The wave front of increased turbulence on the rough wall only reaches the location where it might affect the transition after the onset of transition on the smooth wall. This is likely to be the reason that the transition on the smooth wall in the present transient flow is unaffected.
Figure 10(g–l) shows the development of r.m.s. of turbulent–spatial velocity fluctuations,
![]() $u_{s,rms}^{\prime \prime }$
, for the rough wall. Also shown in the plots are the corresponding data of r.m.s. of turbulent velocity fluctuations,
$u_{s,rms}^{\prime \prime }$
, for the rough wall. Also shown in the plots are the corresponding data of r.m.s. of turbulent velocity fluctuations,
![]() $u_{s,rms}^{\prime }$
. The former measures the fluctuating velocities due to turbulence and the spatial variability due to the presence of the roughness elements. The latter accounts for the turbulent fluctuations only. It is shown that, whereas the r.m.s. of velocity fluctuations obtained from the two averaging approaches collapse on top of each other in the core region (figure 10
h,j,l), there are major differences between them, in particular for the streamwise and wall-normal components, in the region close to the roughness (figure 10
g,i,k). These results and those from other locations (not shown) show that the discrepancies vanish at above
$u_{s,rms}^{\prime }$
. The former measures the fluctuating velocities due to turbulence and the spatial variability due to the presence of the roughness elements. The latter accounts for the turbulent fluctuations only. It is shown that, whereas the r.m.s. of velocity fluctuations obtained from the two averaging approaches collapse on top of each other in the core region (figure 10
h,j,l), there are major differences between them, in particular for the streamwise and wall-normal components, in the region close to the roughness (figure 10
g,i,k). These results and those from other locations (not shown) show that the discrepancies vanish at above
![]() $y/k_{t}\sim 1.3$
,
$y/k_{t}\sim 1.3$
,
![]() $y^{\prime +0}\sim 19$
. This indicates that significant spatial flow variations due to the roughness geometry remain very close to the element.
$y^{\prime +0}\sim 19$
. This indicates that significant spatial flow variations due to the roughness geometry remain very close to the element.

Figure 11. Development of shear stress: (a) smooth wall, profiles of
![]() $\langle \overline{u^{\prime }v^{\prime }}\rangle$
at several instants; (b,c) rough wall, profiles of, respectively,
$\langle \overline{u^{\prime }v^{\prime }}\rangle$
at several instants; (b,c) rough wall, profiles of, respectively,
![]() $\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
and
$\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
and
![]() $\langle \overline{u^{\prime }v^{\prime }}\rangle$
at several instants; (d) rough wall, time variation of
$\langle \overline{u^{\prime }v^{\prime }}\rangle$
at several instants; (d) rough wall, time variation of
![]() $\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
and
$\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
and
![]() $\langle \overline{u^{\prime }v^{\prime }}\rangle$
at several locations close to the rough wall.
$\langle \overline{u^{\prime }v^{\prime }}\rangle$
at several locations close to the rough wall.
The development of the r.m.s. of velocity fluctuations (both
![]() $u_{s,rms}^{\prime }$
and
$u_{s,rms}^{\prime }$
and
![]() $u_{s,rms}^{\prime \prime }$
) on the rough wall in the core region (figure 10
h,j,l) is broadly similar to that on the smooth wall discussed above, except that the latter has a longer delay. For the rough wall, the response at the outer edge of the near-wall region (say
$u_{s,rms}^{\prime \prime }$
) on the rough wall in the core region (figure 10
h,j,l) is broadly similar to that on the smooth wall discussed above, except that the latter has a longer delay. For the rough wall, the response at the outer edge of the near-wall region (say
![]() $y^{\prime +0}=54.6$
) occurs much earlier and the delay increases significantly from that location to the centre of the flow. The behaviour is very different in the near-wall region. Consider the r.m.s. of turbulent–spatial velocity fluctuations (thick lines) first. All three components begin to respond almost immediately after the commencement of the transient, although there are clear differences between them. The
$y^{\prime +0}=54.6$
) occurs much earlier and the delay increases significantly from that location to the centre of the flow. The behaviour is very different in the near-wall region. Consider the r.m.s. of turbulent–spatial velocity fluctuations (thick lines) first. All three components begin to respond almost immediately after the commencement of the transient, although there are clear differences between them. The
![]() $u_{rms}^{\prime \prime }$
at the crest (
$u_{rms}^{\prime \prime }$
at the crest (
![]() $y^{\prime +0}=6.1$
) increases rapidly to reach a peak at
$y^{\prime +0}=6.1$
) increases rapidly to reach a peak at
![]() $t^{\ast }=0.6$
, falling back afterwards, approaching its steady value at around
$t^{\ast }=0.6$
, falling back afterwards, approaching its steady value at around
![]() $t^{\ast }=4$
. The
$t^{\ast }=4$
. The
![]() $u_{rms}^{\prime \prime }$
at
$u_{rms}^{\prime \prime }$
at
![]() $y^{\prime +0}=11.6$
behaves in a similar way but with a small delay and a lower peak. Further from the wall (
$y^{\prime +0}=11.6$
behaves in a similar way but with a small delay and a lower peak. Further from the wall (
![]() $y^{\prime +0}=23.3$
), there is an additional delay and no peak is seen. The
$y^{\prime +0}=23.3$
), there is an additional delay and no peak is seen. The
![]() $v_{rms}^{\prime \prime }$
is similar in terms of the response time, but the peaks at
$v_{rms}^{\prime \prime }$
is similar in terms of the response time, but the peaks at
![]() $y^{\prime +0}=6.1$
and 11.6 are much smaller. In addition, there are strong oscillatory variations at the early times. The increase of
$y^{\prime +0}=6.1$
and 11.6 are much smaller. In addition, there are strong oscillatory variations at the early times. The increase of
![]() $w_{rms}^{\prime \prime }$
is much slower and there is no overshooting. Comparing the formation and growth of the streaks shown in figure 5 with the development of the r.m.s. of streamwise velocity fluctuations, it is concluded that the rapid increase and strong overshooting of
$w_{rms}^{\prime \prime }$
is much slower and there is no overshooting. Comparing the formation and growth of the streaks shown in figure 5 with the development of the r.m.s. of streamwise velocity fluctuations, it is concluded that the rapid increase and strong overshooting of
![]() $u_{rms}^{\prime \prime }$
in the early stage of the transient are largely associated with the formation of strong positive and then negative streaks. The formation of the hairpin vortices also contributes to the development of
$u_{rms}^{\prime \prime }$
in the early stage of the transient are largely associated with the formation of strong positive and then negative streaks. The formation of the hairpin vortices also contributes to the development of
![]() $u_{rms}^{\prime \prime }$
, but this has lesser influence. In contrast, the developments of
$u_{rms}^{\prime \prime }$
, but this has lesser influence. In contrast, the developments of
![]() $v_{rms}^{\prime \prime }$
and
$v_{rms}^{\prime \prime }$
and
![]() $w_{rms}^{\prime \prime }$
are influenced quite strongly by the formation and evolution of the hairpin structures. In particular, these cause the oscillatory behaviour in
$w_{rms}^{\prime \prime }$
are influenced quite strongly by the formation and evolution of the hairpin structures. In particular, these cause the oscillatory behaviour in
![]() $v_{rms}^{\prime \prime }$
and
$v_{rms}^{\prime \prime }$
and
![]() $w_{rms}^{\prime \prime }$
. The early responses of the r.m.s. of turbulent velocity fluctuations (thin lines with symbols) are very different from those described above for the turbulent–spatial velocity fluctuations. All three components appear to respond in a similar way, all with a short delay after the commencement of the transient flow. Most significantly, the early rapid overshooting in
$w_{rms}^{\prime \prime }$
. The early responses of the r.m.s. of turbulent velocity fluctuations (thin lines with symbols) are very different from those described above for the turbulent–spatial velocity fluctuations. All three components appear to respond in a similar way, all with a short delay after the commencement of the transient flow. Most significantly, the early rapid overshooting in
![]() $u_{s,rms}^{\prime \prime }$
is replaced by more gradual changes in
$u_{s,rms}^{\prime \prime }$
is replaced by more gradual changes in
![]() $u_{s,rms}^{\prime }$
. The differences between them reflect the spatial variation of the velocities caused by the roughness topology. These are very strong at the early stages due to the formation of the streaks and vortices directly associated with the roughness elements.
$u_{s,rms}^{\prime }$
. The differences between them reflect the spatial variation of the velocities caused by the roughness topology. These are very strong at the early stages due to the formation of the streaks and vortices directly associated with the roughness elements.
As discussed above, in contrast to the smooth wall in which the wall-normal and spanwise components of the r.m.s. of velocity fluctuations remain almost unchanged for a long time in the pre-transition stage, for the rough wall these components exhibit a response similar to that of the streamwise component, increasing shortly after the commencement of the transient flow. This behaviour is in agreement with the results of the earlier studies on the rough wall, in which the increased wall-normal fluctuation has been discussed as the component that is strongly associated with the near-wall vortical structures, thereby characterising flow behaviour over the rough wall (Orlandi Reference Orlandi2013). For the transition from laminar to turbulent flow over a rough wall, Orlandi (Reference Orlandi2013) showed that the transition occurs once the r.m.s. of wall-normal velocity fluctuations (normalised by instantaneous friction velocity) at the roughness crest is greater than a threshold value of 0.6.
4.4. Turbulent shear stress and quadrant analysis
Figure 11 shows the development of turbulent shear stress at several instants. The turbulent shear stress for the smooth wall (figure 11
a) remains largely unchanged in the early moments of the pre-transition period (
![]() $t^{\ast }<1.6$
), then increases slowly until the onset of transition on the smooth wall (
$t^{\ast }<1.6$
), then increases slowly until the onset of transition on the smooth wall (
![]() $t^{\ast }\sim 8$
). The response becomes much faster during the transition (
$t^{\ast }\sim 8$
). The response becomes much faster during the transition (
![]() $8<t^{\ast }<16$
), approaching the corresponding final steady-flow profile in the wall region; and eventually, it reaches a fully developed shape by
$8<t^{\ast }<16$
), approaching the corresponding final steady-flow profile in the wall region; and eventually, it reaches a fully developed shape by
![]() $t^{\ast }\sim 20$
. The response starts from the wall region and propagates to the core with time.
$t^{\ast }\sim 20$
. The response starts from the wall region and propagates to the core with time.

Figure 12. Development of ensemble-averaged turbulent shear stress (normalised by
![]() $u_{{\it\tau}0}^{2}$
) for an element of figure 2(b) at the roughness crest,
$u_{{\it\tau}0}^{2}$
) for an element of figure 2(b) at the roughness crest,
![]() $y=0$
, and at several instants: (a)
$y=0$
, and at several instants: (a)
![]() $t^{\ast }=0.2$
, (b)
$t^{\ast }=0.2$
, (b)
![]() $t^{\ast }=0.3$
, (c)
$t^{\ast }=0.3$
, (c)
![]() $t^{\ast }=0.4$
, (d)
$t^{\ast }=0.4$
, (d)
![]() $t^{\ast }=0.6$
, (e)
$t^{\ast }=0.6$
, (e)
![]() $t^{\ast }=1.5$
, (f)
$t^{\ast }=1.5$
, (f)
![]() $t^{\ast }=4$
. Dashed lines show the location of
$t^{\ast }=4$
. Dashed lines show the location of
![]() $x/{\it\lambda}=0.35$
.
$x/{\it\lambda}=0.35$
.
The spatially averaged turbulent-spatial shear stress (
![]() $\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
) in the wall region of the rough wall (figure 11
b) initially increases rapidly, overshoots the final steady values, and reaches a peak at
$\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
) in the wall region of the rough wall (figure 11
b) initially increases rapidly, overshoots the final steady values, and reaches a peak at
![]() $t^{\ast }\sim 0.3$
(see also history plot of figure 11
d). Then, during
$t^{\ast }\sim 0.3$
(see also history plot of figure 11
d). Then, during
![]() $0.3<t^{\ast }<0.8$
, the turbulent shear stress profile oscillates strongly before reducing monotonically with time. By
$0.3<t^{\ast }<0.8$
, the turbulent shear stress profile oscillates strongly before reducing monotonically with time. By
![]() $t^{\ast }\sim 4$
, it is approaching its final state in the region of
$t^{\ast }\sim 4$
, it is approaching its final state in the region of
![]() $y^{\prime +0}<30$
(which corresponds to
$y^{\prime +0}<30$
(which corresponds to
![]() $y^{\prime +}<90$
in the mean velocity profiles of figure 9). The large overshoot observed in the near-wall region of the profile is associated with the formation of the strong well-organised roughness-induced hairpin vortices observed in figure 5. Such structures are initially significantly different from ‘conventional’ turbulence. Later, at late pre-transition stage, the structures begin to break down, leading to the generation of more conventional turbulence.
$y^{\prime +}<90$
in the mean velocity profiles of figure 9). The large overshoot observed in the near-wall region of the profile is associated with the formation of the strong well-organised roughness-induced hairpin vortices observed in figure 5. Such structures are initially significantly different from ‘conventional’ turbulence. Later, at late pre-transition stage, the structures begin to break down, leading to the generation of more conventional turbulence.
The development of
![]() $\langle \overline{u^{\prime }v^{\prime }}\rangle$
is shown in figure 11(c). In comparison with the spatially averaged turbulent-spatial shear stress (figure 11
b), the wall-region response of
$\langle \overline{u^{\prime }v^{\prime }}\rangle$
is shown in figure 11(c). In comparison with the spatially averaged turbulent-spatial shear stress (figure 11
b), the wall-region response of
![]() $\langle \overline{u^{\prime }v^{\prime }}\rangle$
is much slower and the large overshooting over the final steady values at the early moments of the transition shown in
$\langle \overline{u^{\prime }v^{\prime }}\rangle$
is much slower and the large overshooting over the final steady values at the early moments of the transition shown in
![]() $\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
(figure 11
b) are not seen here. It starts to respond at
$\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
(figure 11
b) are not seen here. It starts to respond at
![]() $y^{\prime +0}\sim 5$
(just below the crest), at
$y^{\prime +0}\sim 5$
(just below the crest), at
![]() $t^{\ast }\sim 0.25$
, developing a peak that increases and moves towards the core, reaching
$t^{\ast }\sim 0.25$
, developing a peak that increases and moves towards the core, reaching
![]() $y^{\prime +0}\sim 15$
at
$y^{\prime +0}\sim 15$
at
![]() $t^{\ast }\sim 0.4$
. Between
$t^{\ast }\sim 0.4$
. Between
![]() $0.4<t^{\ast }<1.5$
, the peak value increases while its
$0.4<t^{\ast }<1.5$
, the peak value increases while its
![]() $y$
location remains largely unchanged. Thereafter, the peak value reduces slightly but the values increase further away from the wall (
$y$
location remains largely unchanged. Thereafter, the peak value reduces slightly but the values increase further away from the wall (
![]() $y^{\prime +0}\sim 20$
) until
$y^{\prime +0}\sim 20$
) until
![]() $t^{\ast }\sim 4$
, when, similar to
$t^{\ast }\sim 4$
, when, similar to
![]() $\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
, the near-wall values approach the corresponding final steady-state flow, and the core region values reach the corresponding final-state values with further delays.
$\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
, the near-wall values approach the corresponding final steady-state flow, and the core region values reach the corresponding final-state values with further delays.
Figure 11(d) shows the time variation of both turbulent and turbulent-spatial shear stresses at several locations close to the rough wall. Strong oscillations in
![]() $\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
can be seen clearly at the crest during the initial stages (until
$\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
can be seen clearly at the crest during the initial stages (until
![]() $t^{\ast }\sim 0.8$
). Such strong oscillations, which are similar to those observed for
$t^{\ast }\sim 0.8$
). Such strong oscillations, which are similar to those observed for
![]() $v_{rms}^{\prime \prime }$
and, to a lesser extent, for
$v_{rms}^{\prime \prime }$
and, to a lesser extent, for
![]() $w_{rms}^{\prime \prime }$
in figure 10(g,i,k), are absent in
$w_{rms}^{\prime \prime }$
in figure 10(g,i,k), are absent in
![]() $\langle \overline{u^{\prime }v^{\prime }}\rangle$
. The spatially averaged turbulent-spatial shear stress,
$\langle \overline{u^{\prime }v^{\prime }}\rangle$
. The spatially averaged turbulent-spatial shear stress,
![]() $\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
, in the locations very close to the roughness, is the sum of the spatially averaged turbulent shear stress,
$\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
, in the locations very close to the roughness, is the sum of the spatially averaged turbulent shear stress,
![]() $\langle \overline{u^{\prime }v^{\prime }}\rangle$
, and a so-called dispersive (or form-induced) stress, which results from the roughness geometry. Whereas a significant discrepancy is exhibited between
$\langle \overline{u^{\prime }v^{\prime }}\rangle$
, and a so-called dispersive (or form-induced) stress, which results from the roughness geometry. Whereas a significant discrepancy is exhibited between
![]() $\langle \overline{u^{\prime }v^{\prime }}\rangle$
and
$\langle \overline{u^{\prime }v^{\prime }}\rangle$
and
![]() $\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
for
$\langle \overline{u^{\prime \prime }v^{\prime \prime }}\rangle$
for
![]() $y/k_{t}=0,0.6$
, in the early stages of transient flow (
$y/k_{t}=0,0.6$
, in the early stages of transient flow (
![]() $t^{\ast }<0.8$
), the values collapse for the corresponding profile at
$t^{\ast }<0.8$
), the values collapse for the corresponding profile at
![]() $y/k_{t}=1.8$
. In fact, an inspection of the results at all locations (not shown) indicates that, similar to the r.m.s. of velocity fluctuations, the discrepancy between the two stresses disappears for locations above
$y/k_{t}=1.8$
. In fact, an inspection of the results at all locations (not shown) indicates that, similar to the r.m.s. of velocity fluctuations, the discrepancy between the two stresses disappears for locations above
![]() $y/k_{t}\sim 1.3$
, indicating a negligible effect of dispersive stress in that region.
$y/k_{t}\sim 1.3$
, indicating a negligible effect of dispersive stress in that region.

Figure 13. Ensemble-averaged turbulent shear stress, and sweep and ejection events during the transient flow for the
![]() $y$
–
$y$
–
![]() $z$
plane at
$z$
plane at
![]() $x/{\it\lambda}=0.35$
. Plots are shaded by: (a–d)
$x/{\it\lambda}=0.35$
. Plots are shaded by: (a–d)
![]() $\overline{u^{\prime }v^{\prime }}^{+0}$
; (e–h)
$\overline{u^{\prime }v^{\prime }}^{+0}$
; (e–h)
![]() $\overline{u^{\prime }v^{\prime }}_{(Q2,h4)}^{+0}$
(strong ejections); (i–l)
$\overline{u^{\prime }v^{\prime }}_{(Q2,h4)}^{+0}$
(strong ejections); (i–l)
![]() $\overline{u^{\prime }v^{\prime }}_{(Q4,h4)}^{+0}$
(strong sweep). Contour lines of
$\overline{u^{\prime }v^{\prime }}_{(Q4,h4)}^{+0}$
(strong sweep). Contour lines of
![]() $\overline{u^{\prime }v^{\prime }}^{+0}$
are also shown in each plot (negative values shown by dashed lines): (a,e,i)
$\overline{u^{\prime }v^{\prime }}^{+0}$
are also shown in each plot (negative values shown by dashed lines): (a,e,i)
![]() $t^{\ast }=0.3$
, (b,f,j)
$t^{\ast }=0.3$
, (b,f,j)
![]() $t^{\ast }=0.4$
, (c,g,k)
$t^{\ast }=0.4$
, (c,g,k)
![]() $t^{\ast }=0.6$
, (d,h,l)
$t^{\ast }=0.6$
, (d,h,l)
![]() $t^{\ast }=4$
.
$t^{\ast }=4$
.
The influence of the primary vortex is further investigated in figure 12, which shows the contours of the ensemble-averaged
![]() $\overline{u^{\prime }v^{\prime }}$
over a horizontal plane at the crest. The footprint is a whole element as shown in figure 2(b). At
$\overline{u^{\prime }v^{\prime }}$
over a horizontal plane at the crest. The footprint is a whole element as shown in figure 2(b). At
![]() $t^{\ast }=0.2$
, an area of high turbulent shear stress (the dark patch) is seen just behind the roughness crest, indicating the initiation of the primary vortex at this location. This strong turbulent shear stress region is then convected downstream. Consistent with the vortex and vector plots (figures 5–7), the signature of the head of a hairpin can be seen in the frame at
$t^{\ast }=0.2$
, an area of high turbulent shear stress (the dark patch) is seen just behind the roughness crest, indicating the initiation of the primary vortex at this location. This strong turbulent shear stress region is then convected downstream. Consistent with the vortex and vector plots (figures 5–7), the signature of the head of a hairpin can be seen in the frame at
![]() $t^{\ast }=0.3$
, in the sense that there is a high value region of turbulent shear stress which coincides with the hairpin location detected at this instant. At
$t^{\ast }=0.3$
, in the sense that there is a high value region of turbulent shear stress which coincides with the hairpin location detected at this instant. At
![]() $t^{\ast }=0.4$
, the large dark patch has disappeared, replaced by two long thinner regions. Note the periodic nature of the plots: the two dark patches in quadrants 2 and 3 can be seen as the continuation of those in quadrants 1 and 4. These thin regions can be associated with the legs of the counter-rotating vortex (see also figure 13). This is consistent with figure 6(b–g), which shows that the hairpin heads are ejected away from this elevation by this time, leaving behind the hairpin legs. At
$t^{\ast }=0.4$
, the large dark patch has disappeared, replaced by two long thinner regions. Note the periodic nature of the plots: the two dark patches in quadrants 2 and 3 can be seen as the continuation of those in quadrants 1 and 4. These thin regions can be associated with the legs of the counter-rotating vortex (see also figure 13). This is consistent with figure 6(b–g), which shows that the hairpin heads are ejected away from this elevation by this time, leaving behind the hairpin legs. At
![]() $t^{\ast }=0.6$
, the thinner dark patches are, similarly, associated with the remaining parts of trailing hairpin legs that are about to be ejected away from the crest. At
$t^{\ast }=0.6$
, the thinner dark patches are, similarly, associated with the remaining parts of trailing hairpin legs that are about to be ejected away from the crest. At
![]() $t^{\ast }=1.5$
, the primary vortex has left this elevation and the shear stress distribution is closely similar to that of the flow at
$t^{\ast }=1.5$
, the primary vortex has left this elevation and the shear stress distribution is closely similar to that of the flow at
![]() $t^{\ast }=4$
. In addition, the distribution of the steady flow (
$t^{\ast }=4$
. In addition, the distribution of the steady flow (
![]() $t^{\ast }=27.2$
; not shown), which is similar to that at
$t^{\ast }=27.2$
; not shown), which is similar to that at
![]() $t^{\ast }=4$
, is consistent with the experimental results of Hong et al. (Reference Hong, Katz and Schultz2011) and Talapatra & Katz (Reference Talapatra and Katz2013), which show that the forward side of the element is a region of strong positive shear stress.
$t^{\ast }=4$
, is consistent with the experimental results of Hong et al. (Reference Hong, Katz and Schultz2011) and Talapatra & Katz (Reference Talapatra and Katz2013), which show that the forward side of the element is a region of strong positive shear stress.
Quadrant analysis is a useful tool for studying the contribution of various flow events to the total turbulence production. Using the definition of the hyperbolic hole introduced by Lu & Willmarth (Reference Lu and Willmarth1973), the contribution of each quadrant to
![]() $\overline{u^{\prime }v^{\prime }}$
is defined as
$\overline{u^{\prime }v^{\prime }}$
is defined as
where
![]() $I(t)$
is an indicator function defined so that
$I(t)$
is an indicator function defined so that
The greater the value of
![]() $h$
, the stronger the events. Here, we have carried out ensemble-averaged quadrant analysis, and so the integral is carried out over a number of wavelengths in any horizontal plane rather than over time as defined in (4.6).
$h$
, the stronger the events. Here, we have carried out ensemble-averaged quadrant analysis, and so the integral is carried out over a number of wavelengths in any horizontal plane rather than over time as defined in (4.6).
Figure 13 shows the development of ensemble-averaged (a–d) turbulent shear stress,
![]() $\overline{u^{\prime }v^{\prime }}$
, (e–h) strong ejection events,
$\overline{u^{\prime }v^{\prime }}$
, (e–h) strong ejection events,
![]() $\overline{u^{\prime }v^{\prime }}_{(Q2,h4)}$
, and (i–l) strong sweep events,
$\overline{u^{\prime }v^{\prime }}_{(Q2,h4)}$
, and (i–l) strong sweep events,
![]() $\overline{u^{\prime }v^{\prime }}_{(Q4,h4)}$
, for the
$\overline{u^{\prime }v^{\prime }}_{(Q4,h4)}$
, for the
![]() $y$
–
$y$
–
![]() $z$
plane at
$z$
plane at
![]() $x/{\it\lambda}=0.35$
at several instants. The location of the plane is shown in figure 12 as dashed lines. At
$x/{\it\lambda}=0.35$
at several instants. The location of the plane is shown in figure 12 as dashed lines. At
![]() $t^{\ast }=4$
when the near-roughness flow has reached the steady-state condition of the final flow, strong turbulent shear stress exhibits above the forward side (red patch), along the ridge line of the roughness element. This distribution is consistent with the experimental results of Hong et al. (Reference Hong, Katz and Schultz2011) for flow structure over a pyramid roughness in the steady-flow condition. The locus of the strong turbulent shear stress for the first three instants is consistent with the high-stress area seen in figure 12, and is associated with primary counter-rotating vortices that exist at these moments (figure 5). This shows that, although vortices of various strengths are formed behind each roughness element, the primary vortex has the most striking impact on the local turbulence structure in the early stages of the transient flow. During this period, the areas of strong ejection events (green areas in figure 13
e–h) are correlated with the most intense turbulent stress regions, whereas the strong sweep events (figure 13
i–l) are not associated with the regions of high turbulent stress. According to the contour levels in these plots (ranging from 0 to 0.3), it can be seen that more than 30 % of the total positive shear stress comes from those events. That is, the dominant contribution to shear stresses in these early stages is from the violent ejection events. This correlation remains true until
$t^{\ast }=4$
when the near-roughness flow has reached the steady-state condition of the final flow, strong turbulent shear stress exhibits above the forward side (red patch), along the ridge line of the roughness element. This distribution is consistent with the experimental results of Hong et al. (Reference Hong, Katz and Schultz2011) for flow structure over a pyramid roughness in the steady-flow condition. The locus of the strong turbulent shear stress for the first three instants is consistent with the high-stress area seen in figure 12, and is associated with primary counter-rotating vortices that exist at these moments (figure 5). This shows that, although vortices of various strengths are formed behind each roughness element, the primary vortex has the most striking impact on the local turbulence structure in the early stages of the transient flow. During this period, the areas of strong ejection events (green areas in figure 13
e–h) are correlated with the most intense turbulent stress regions, whereas the strong sweep events (figure 13
i–l) are not associated with the regions of high turbulent stress. According to the contour levels in these plots (ranging from 0 to 0.3), it can be seen that more than 30 % of the total positive shear stress comes from those events. That is, the dominant contribution to shear stresses in these early stages is from the violent ejection events. This correlation remains true until
![]() $t^{\ast }\sim 0.8$
(not shown), when the primary vortex is ejected from the element surface. In contrast, at
$t^{\ast }\sim 0.8$
(not shown), when the primary vortex is ejected from the element surface. In contrast, at
![]() $t^{\ast }=4$
and in the region close to the rough element, neither are the ejections the dominant events nor is the influence of the strong primary hairpin exhibited. This is in agreement with many studies of steady flow over a rough wall, which show that, in the region very close to the rough element, sweep events make the dominant contribution to turbulent shear stress.
$t^{\ast }=4$
and in the region close to the rough element, neither are the ejections the dominant events nor is the influence of the strong primary hairpin exhibited. This is in agreement with many studies of steady flow over a rough wall, which show that, in the region very close to the rough element, sweep events make the dominant contribution to turbulent shear stress.

Figure 14. Development of Reynolds stress anisotropy at several instants. (a–f) For a smooth wall: (a)
![]() $t^{\ast }=0$
, (b)
$t^{\ast }=0$
, (b)
![]() $t^{\ast }=0.17$
, (c)
$t^{\ast }=0.17$
, (c)
![]() $t^{\ast }=4$
, (d)
$t^{\ast }=4$
, (d)
![]() $t^{\ast }=8$
, (e)
$t^{\ast }=8$
, (e)
![]() $t^{\ast }=16$
, (f)
$t^{\ast }=16$
, (f)
![]() $t^{\ast }=27.2$
. (g–l) For a rough wall: (g)
$t^{\ast }=27.2$
. (g–l) For a rough wall: (g)
![]() $t^{\ast }=0$
, (h)
$t^{\ast }=0$
, (h)
![]() $t^{\ast }=0.17$
, (i)
$t^{\ast }=0.17$
, (i)
![]() $t^{\ast }=0.4$
, (j)
$t^{\ast }=0.4$
, (j)
![]() $t^{\ast }=0.8$
, (k)
$t^{\ast }=0.8$
, (k)
![]() $t^{\ast }=1.5$
, (l)
$t^{\ast }=1.5$
, (l)
![]() $t^{\ast }=4$
; arrows, from small to big, denote the values at the bottom of the channel, crest and channel centre. (m) Distribution of the invariant function
$t^{\ast }=4$
; arrows, from small to big, denote the values at the bottom of the channel, crest and channel centre. (m) Distribution of the invariant function
![]() $F$
at the crest at
$F$
at the crest at
![]() $t^{\ast }=0.4$
. The plot is shaded by value of
$t^{\ast }=0.4$
. The plot is shaded by value of
![]() $F$
, and contour lines of
$F$
, and contour lines of
![]() $\overline{u^{\prime }v^{\prime }}$
are also shown.
$\overline{u^{\prime }v^{\prime }}$
are also shown.
4.5. Anisotropy
Turbulence anisotropy can be examined by studying anisotropy-invariant maps (AIMs) of the Reynolds stress anisotropy tensor (
![]() $\unicode[STIX]{x1D623}_{ij}$
), which is defined as
$\unicode[STIX]{x1D623}_{ij}$
), which is defined as
where
![]() ${\it\delta}_{ij}$
is the Kronecker delta tensor. An AIM proposed by Lumley (Reference Lumley1978) is constructed using the second and third principal invariants, respectively defined as
${\it\delta}_{ij}$
is the Kronecker delta tensor. An AIM proposed by Lumley (Reference Lumley1978) is constructed using the second and third principal invariants, respectively defined as
![]() $-\text{II}=(\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ji})/2$
and
$-\text{II}=(\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ji})/2$
and
![]() $\text{III}=(\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{jk}\unicode[STIX]{x1D623}_{ki})/3$
. These parameters, which are independent of coordinate choice for analysing the overall anisotropy, provide information on turbulence streaky structures and are useful in developing turbulence modelling. In addition, since these normalised parameters are not dependent on the friction velocity, they can be of interest in experimental studies where the friction velocity is not available.
$\text{III}=(\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{jk}\unicode[STIX]{x1D623}_{ki})/3$
. These parameters, which are independent of coordinate choice for analysing the overall anisotropy, provide information on turbulence streaky structures and are useful in developing turbulence modelling. In addition, since these normalised parameters are not dependent on the friction velocity, they can be of interest in experimental studies where the friction velocity is not available.
Figure 14(a–l) shows the AIM profiles, at several instants, for flow over the smooth and rough walls, respectively. For the smooth wall (figure 14
a–f), soon after the commencement of the transient, the turbulence in the wall region begins shifting towards one-component turbulence (the top right vertex). This trend reflects the presence of elongated steaks in the pre-transition stage. From late pre-transition (
![]() $t^{\ast }\sim 5.5$
), the values of
$t^{\ast }\sim 5.5$
), the values of
![]() $\text{II}$
begin to reduce, and the points move along the right-hand boundary, indicating that the turbulence is becoming axisymmetric. At
$\text{II}$
begin to reduce, and the points move along the right-hand boundary, indicating that the turbulence is becoming axisymmetric. At
![]() $t^{\ast }=16$
and later, the turbulence state is characteristic of a steady flow. The AIM profiles for the rough wall are shown in figure 14(g–l). Three arrows in each panel, from small to big in size, respectively, indicate the value at the bottom of the channel, at the roughness crest and at the centre of the channel (
$t^{\ast }=16$
and later, the turbulence state is characteristic of a steady flow. The AIM profiles for the rough wall are shown in figure 14(g–l). Three arrows in each panel, from small to big in size, respectively, indicate the value at the bottom of the channel, at the roughness crest and at the centre of the channel (
![]() ${\it\delta}_{t}$
). At
${\it\delta}_{t}$
). At
![]() $t^{\ast }=0$
, the AIM values for the locations within the roughness height mainly follow the top right line, which characterises the two-component turbulence state, indicating a negligible contribution of the wall-normal velocity. The values exhibit the following changes during the transient flow. Soon after the transient begins (
$t^{\ast }=0$
, the AIM values for the locations within the roughness height mainly follow the top right line, which characterises the two-component turbulence state, indicating a negligible contribution of the wall-normal velocity. The values exhibit the following changes during the transient flow. Soon after the transient begins (
![]() $t^{\ast }\sim 0.17$
), the values move towards the right boundary line, which represents a rod-like (cigar-shaped) axisymmetric turbulence state. This turbulence state, which is exhibited until the beginning of the second stage (
$t^{\ast }\sim 0.17$
), the values move towards the right boundary line, which represents a rod-like (cigar-shaped) axisymmetric turbulence state. This turbulence state, which is exhibited until the beginning of the second stage (
![]() $t^{\ast }\sim 0.8$
), indicates that the two turbulent components should be similar. The r.m.s. of turbulent velocity fluctuations of figure 10(g,i,k) confirm that the values of wall-normal and spanwise components are almost the same during this period. From
$t^{\ast }\sim 0.8$
), indicates that the two turbulent components should be similar. The r.m.s. of turbulent velocity fluctuations of figure 10(g,i,k) confirm that the values of wall-normal and spanwise components are almost the same during this period. From
![]() $t^{\ast }\sim 0.8$
, the AIM values move away from the right boundary line towards the top right line. The AIM developments also show that the value of
$t^{\ast }\sim 0.8$
, the AIM values move away from the right boundary line towards the top right line. The AIM developments also show that the value of
![]() $\text{II}$
for the roughness crest reduces monotonically until
$\text{II}$
for the roughness crest reduces monotonically until
![]() $t^{\ast }\sim 1.5$
, from which point it remains almost unchanged for the rest of the transient flow.
$t^{\ast }\sim 1.5$
, from which point it remains almost unchanged for the rest of the transient flow.
One way of examining the overall anisotropy is via the invariant function,
![]() $F=27\text{III}+9\text{II}+1$
(Lumley Reference Lumley1978). Here
$F=27\text{III}+9\text{II}+1$
(Lumley Reference Lumley1978). Here
![]() $F=0$
denotes two-component turbulence, while
$F=0$
denotes two-component turbulence, while
![]() $F=1$
indicates an isotropic state. Figure 14(m) shows the distribution of the invariant function at the roughness crest for
$F=1$
indicates an isotropic state. Figure 14(m) shows the distribution of the invariant function at the roughness crest for
![]() $t^{\ast }=0.4$
. Also shown in the plot is the contour lines of the ensemble average of the wall-normal stress,
$t^{\ast }=0.4$
. Also shown in the plot is the contour lines of the ensemble average of the wall-normal stress,
![]() $\overline{u^{\prime }v^{\prime }}$
. It is seen that the locus of the strong wall-normal stress corresponds to the lowest anisotropy. These areas are associated with the hairpin legs shown in figure 12(c).
$\overline{u^{\prime }v^{\prime }}$
. It is seen that the locus of the strong wall-normal stress corresponds to the lowest anisotropy. These areas are associated with the hairpin legs shown in figure 12(c).

Figure 15. Development of pre-multiplied spectra for
![]() $\langle \overline{u^{\prime }u^{\prime }}\rangle$
in the streamwise direction. (a–f) Spectra at several instants: (a)
$\langle \overline{u^{\prime }u^{\prime }}\rangle$
in the streamwise direction. (a–f) Spectra at several instants: (a)
![]() $t^{\ast }=0$
, (b)
$t^{\ast }=0$
, (b)
![]() $t^{\ast }=0.17$
, (c)
$t^{\ast }=0.17$
, (c)
![]() $t^{\ast }=0.6$
, (d)
$t^{\ast }=0.6$
, (d)
![]() $t^{\ast }=1.5$
, (e)
$t^{\ast }=1.5$
, (e)
![]() $t^{\ast }=4$
, (f)
$t^{\ast }=4$
, (f)
![]() $t^{\ast }=27.2$
. (g) Time history of the first four dominant wavenumbers (
$t^{\ast }=27.2$
. (g) Time history of the first four dominant wavenumbers (
![]() ${\it\lambda}$
,
${\it\lambda}$
,
![]() $2{\it\lambda}$
,
$2{\it\lambda}$
,
![]() $3{\it\lambda}$
,
$3{\it\lambda}$
,
![]() $5{\it\lambda}$
) at the crest of element,
$5{\it\lambda}$
) at the crest of element,
![]() $y=0$
. (h) Development of the spectrum of the fundamental wavelength (
$y=0$
. (h) Development of the spectrum of the fundamental wavelength (
![]() ${\it\lambda}$
).
${\it\lambda}$
).
4.6. Energy spectra
To examine further the influence of the roughness on the development of the turbulence structure, pre-multiplied streamwise energy spectra are presented in figure 15. The energy spectra of the streamwise normal stress,
![]() $E_{11}$
, are defined such that
$E_{11}$
, are defined such that
The main influence of roughness on the streamwise energy spectra (figure 15
a–f) during the early stages of the transient flow is the presence of spikes at a wavenumber of
![]() $k_{{\it\lambda}}=2{\rm\pi}/{\it\lambda}=20.94$
(wavenumber corresponding to the roughness wavelength,
$k_{{\it\lambda}}=2{\rm\pi}/{\it\lambda}=20.94$
(wavenumber corresponding to the roughness wavelength,
![]() ${\it\lambda}=0.3$
) and its multiples. However, it is seen from the figure that, at the initial and final time instants (
${\it\lambda}=0.3$
) and its multiples. However, it is seen from the figure that, at the initial and final time instants (
![]() $t^{\ast }=0$
,
$t^{\ast }=0$
,
![]() $t^{\ast }=27.2$
), there is no evidence of such spikes. This suggests that, for a steady flow, the
$t^{\ast }=27.2$
), there is no evidence of such spikes. This suggests that, for a steady flow, the
![]() $\langle \overline{u^{\prime }u^{\prime }}\rangle$
spectra do not exhibit any strong signature of the roughness element anywhere above the crest.
$\langle \overline{u^{\prime }u^{\prime }}\rangle$
spectra do not exhibit any strong signature of the roughness element anywhere above the crest.
Soon after the commencement of the transient (
![]() $t^{\ast }=0.17$
), whereas the profiles at
$t^{\ast }=0.17$
), whereas the profiles at
![]() $y/k_{t}=0.6$
and above remain almost unchanged, a big response is exhibited at the roughness crest. The structures with wavenumbers corresponding to the roughness wavelength of
$y/k_{t}=0.6$
and above remain almost unchanged, a big response is exhibited at the roughness crest. The structures with wavenumbers corresponding to the roughness wavelength of
![]() ${\it\lambda}=0.3$
and, to a lesser extent, its subharmonics are clearly shown. At
${\it\lambda}=0.3$
and, to a lesser extent, its subharmonics are clearly shown. At
![]() $t^{\ast }=0.6$
, the response at
$t^{\ast }=0.6$
, the response at
![]() ${\it\lambda}=0.3$
becomes more pronounced, exhibiting a big spike at the roughness wavelength. Meanwhile, the spectra for other wavenumbers have also responded to the transient, but with much smaller strength. These reflect the fact that the primary vortices and other flow structures, which are generated around individual roughness elements, appear periodically along the streamwise direction in the same wavelength as that of the roughness element during these early times, making a huge contribution to this turbulent quantity
${\it\lambda}=0.3$
becomes more pronounced, exhibiting a big spike at the roughness wavelength. Meanwhile, the spectra for other wavenumbers have also responded to the transient, but with much smaller strength. These reflect the fact that the primary vortices and other flow structures, which are generated around individual roughness elements, appear periodically along the streamwise direction in the same wavelength as that of the roughness element during these early times, making a huge contribution to this turbulent quantity
![]() $\langle \overline{u^{\prime }u^{\prime }}\rangle$
. This is consistent with figure 5, in which two pairs of high- and low-speed streaks and trains of quasi-streamwise vortices appear along every element. Another thing to be noted is that no spikes are detected in the spectrum at
$\langle \overline{u^{\prime }u^{\prime }}\rangle$
. This is consistent with figure 5, in which two pairs of high- and low-speed streaks and trains of quasi-streamwise vortices appear along every element. Another thing to be noted is that no spikes are detected in the spectrum at
![]() $y/k_{t}=5.2$
. This is consistent with the observation from the vector plots (figure 7) that the direct influence of the roughness topography at the early stages is confined to a distance of
$y/k_{t}=5.2$
. This is consistent with the observation from the vector plots (figure 7) that the direct influence of the roughness topography at the early stages is confined to a distance of
![]() $y/k_{t}\sim 3$
. It is interesting to note that, at
$y/k_{t}\sim 3$
. It is interesting to note that, at
![]() $t^{\ast }=0.6$
and subsequent instants, the profiles at
$t^{\ast }=0.6$
and subsequent instants, the profiles at
![]() $y/k_{t}=0$
and 0.6 overlap each other. At
$y/k_{t}=0$
and 0.6 overlap each other. At
![]() $t^{\ast }=1.5$
, all spikes have disappeared. It is interesting to see that, at
$t^{\ast }=1.5$
, all spikes have disappeared. It is interesting to see that, at
![]() $t^{\ast }=4$
, the energy spectra of structures with
$t^{\ast }=4$
, the energy spectra of structures with
![]() $k_{x}>10$
at locations up to
$k_{x}>10$
at locations up to
![]() $y/k_{t}=5.2$
have almost reached their corresponding steady-flow values (
$y/k_{t}=5.2$
have almost reached their corresponding steady-flow values (
![]() $t^{\ast }=27.2$
).
$t^{\ast }=27.2$
).
To examine the development of the spectra further, time histories of the pre-multiplied streamwise energy for the first four most dominant wavenumbers at the crest level (
![]() $y/k_{t}=0$
) are shown in figure 15(g). It is seen that the energy spectrum at
$y/k_{t}=0$
) are shown in figure 15(g). It is seen that the energy spectrum at
![]() $k_{x}=k_{{\it\lambda}}$
increases after the transient flow begins, which continues until
$k_{x}=k_{{\it\lambda}}$
increases after the transient flow begins, which continues until
![]() $t^{\ast }\sim 0.3$
. It then decreases half-way by
$t^{\ast }\sim 0.3$
. It then decreases half-way by
![]() $t^{\ast }\sim 0.4$
, when it begins a sharp increase, exhibiting a peak at
$t^{\ast }\sim 0.4$
, when it begins a sharp increase, exhibiting a peak at
![]() $t^{\ast }=0.7$
. The peak value of the streamwise spectrum associated with
$t^{\ast }=0.7$
. The peak value of the streamwise spectrum associated with
![]() $k_{x}=k_{{\it\lambda}}$
is approximately four times that of the second wavenumber
$k_{x}=k_{{\it\lambda}}$
is approximately four times that of the second wavenumber
![]() $k_{x}=2k_{{\it\lambda}}$
(i.e.
$k_{x}=2k_{{\it\lambda}}$
(i.e.
![]() $(E_{k_{{\it\lambda}}}/E_{k_{2{\it\lambda}}})_{x,max}\approx 4$
). At later times, the spectrum decreases monotonically, approaching the steady value at
$(E_{k_{{\it\lambda}}}/E_{k_{2{\it\lambda}}})_{x,max}\approx 4$
). At later times, the spectrum decreases monotonically, approaching the steady value at
![]() $t^{\ast }\sim 1.5$
. A close inspection of the vortex (figure 5) and the contour plots of figure 12 (
$t^{\ast }\sim 1.5$
. A close inspection of the vortex (figure 5) and the contour plots of figure 12 (
![]() $t^{\ast }=0.3$
), show that the initial increase, until
$t^{\ast }=0.3$
), show that the initial increase, until
![]() $t^{\ast }=0.3$
, is associated with the period during which the well-defined primary hairpins are being formed. The period of
$t^{\ast }=0.3$
, is associated with the period during which the well-defined primary hairpins are being formed. The period of
![]() $0.3<t^{\ast }<0.4$
corresponds to times when the primary hairpin is just generated within each element and its head passes up the crest of the roughness, while the associated energetic trailing legs have not yet reached this level. The sharp increase at
$0.3<t^{\ast }<0.4$
corresponds to times when the primary hairpin is just generated within each element and its head passes up the crest of the roughness, while the associated energetic trailing legs have not yet reached this level. The sharp increase at
![]() $0.4<t^{\ast }<0.71$
corresponds to the period in which the trailing legs pass over the roughness wavelength, and move upwards towards the crest level of successive roughness. By
$0.4<t^{\ast }<0.71$
corresponds to the period in which the trailing legs pass over the roughness wavelength, and move upwards towards the crest level of successive roughness. By
![]() $t^{\ast }=0.7$
, most parts of the legs of the vortical structures have moved away from the wall, and so a gradual reduction is exhibited at later times, leading to steady-flow values for this location at
$t^{\ast }=0.7$
, most parts of the legs of the vortical structures have moved away from the wall, and so a gradual reduction is exhibited at later times, leading to steady-flow values for this location at
![]() $t^{\ast }\sim 1.6$
.
$t^{\ast }\sim 1.6$
.
Figure 15(h) shows the development of the energy spectra associated with the fundamental wavelength
![]() $k_{x}=k_{{\it\lambda}}$
for the locations up to
$k_{x}=k_{{\it\lambda}}$
for the locations up to
![]() $y/k_{t}=5$
. An area of high-energy spectra is seen for the locations up to
$y/k_{t}=5$
. An area of high-energy spectra is seen for the locations up to
![]() $y/k_{t}\sim 1.5$
during
$y/k_{t}\sim 1.5$
during
![]() $0.3<t^{\ast }<0.8$
. Consistent with the profiles of figure 15(a–f) and visualisations of figure 5, this indicates that the strong influence of the fundamental wavelength is restricted up to
$0.3<t^{\ast }<0.8$
. Consistent with the profiles of figure 15(a–f) and visualisations of figure 5, this indicates that the strong influence of the fundamental wavelength is restricted up to
![]() $y/k_{t}\sim 3$
and the effect lasts until
$y/k_{t}\sim 3$
and the effect lasts until
![]() $t^{\ast }\sim 0.8$
, when the major breakdown of the primary hairpin structures starts to occur.
$t^{\ast }\sim 0.8$
, when the major breakdown of the primary hairpin structures starts to occur.
5. Conclusions
Direct numerical simulation was performed of a transient flow in a channel consisting of a rough bottom wall made of close-packed 3D pyramid roughness and a smooth top wall. The unsteady flow started from an initially statistically steady turbulent flow with
![]() $\mathit{Re}=2800$
and increased linearly, within a very short time, to a final Reynolds number of
$\mathit{Re}=2800$
and increased linearly, within a very short time, to a final Reynolds number of
![]() $\mathit{Re}=7400$
. The corresponding equivalent sand roughness Reynolds number for the initial and final flows are respectively
$\mathit{Re}=7400$
. The corresponding equivalent sand roughness Reynolds number for the initial and final flows are respectively
![]() $k_{s}^{+}=14.5$
and
$k_{s}^{+}=14.5$
and
![]() $k_{s}^{+}=41.5$
.
$k_{s}^{+}=41.5$
.
-
(1) It has been shown that the turbulent–turbulent transient flow over the pyramid-roughened wall concerned following a rapid flow increase undergoes a process that resembles a roughness-induced laminar–turbulent transition.
-
(2) Immediately after the acceleration ends, the induced change behaves in a ‘plug-flow’ manner: the velocity of the perturbation flow is uniform above the roughness crest, but below the crest it reduces linearly to zero at the bottom of the roughness. Such a perturbation flow then interacts with the roughness elements, resulting in a series of events that are similar to those observed in a roughness-induced laminar–turbulent transition.
-
(3) The transition for the rough wall is in the form of a single cycle of birth, evolution and breakdown of strong primary counter-rotating hairpin structures. Over each roughness element, a vortex is formed with its head behind the roughness crest and its legs alongside the ridge lines. In time, these head-up vortices convect downstream. Violent ejection events are present in the space between the two legs, while sweep events are present in between the vortices. Most of the strong hairpin structures lift up to the upper layers and break down before
 $t^{\ast }\sim 4$
. In addition to the generation of primary vortices, positive and negative streaks are produced and these break up at the same time as the vortices break down. Soon after (
$t^{\ast }\sim 4$
. In addition to the generation of primary vortices, positive and negative streaks are produced and these break up at the same time as the vortices break down. Soon after (
 $t^{\ast }\sim 4$
), the flow near the wall has reached its new turbulence state and the primary process of the transition is complete. Significant further time (
$t^{\ast }\sim 4$
), the flow near the wall has reached its new turbulence state and the primary process of the transition is complete. Significant further time (
 $t^{\ast }\sim 27.2$
) is needed for the new turbulence to propagate into the core of the channel flow.
$t^{\ast }\sim 27.2$
) is needed for the new turbulence to propagate into the core of the channel flow. -
(4) The vortices generated around the close-packed roughness elements resemble the hairpin structures formed over isolated roughness in the transition of a laminar boundary layer (Acarlar & Smith Reference Acarlar and Smith1987).
-
(5) The flow over the upper smooth wall of the channel undergoes bypass transition that is closely similar to that reported by He & Seddighi (Reference He and Seddighi2013) for a wholly smooth channel (i.e. both walls smooth). That is, the three distinct transition processes, namely pre-transition (
 $t^{\ast }<8$
), transition (
$t^{\ast }<8$
), transition (
 $8<t^{\ast }<16$
) and fully developed turbulence (
$8<t^{\ast }<16$
) and fully developed turbulence (
 $t^{\ast }>16$
), identified for the wholly smooth channel, are also observed here. It is especially noteworthy that the much earlier transition on the opposite rough wall has no significant effect on the timing and process of the transition on the smooth wall.
$t^{\ast }>16$
), identified for the wholly smooth channel, are also observed here. It is especially noteworthy that the much earlier transition on the opposite rough wall has no significant effect on the timing and process of the transition on the smooth wall. -
(6) Energy spectra and vector plots show that the most significant direct influence of the roughness elements in the transient process is confined within a region up to
 $y/k_{t}\sim 3$
above the roughness crests.
$y/k_{t}\sim 3$
above the roughness crests. -
(7) Owing to the rapid initial increase in wall shear stress, the mean velocity over the rough wall expressed in wall units shows a rapid reduction, similar to that for the smooth wall. In contrast to the smooth wall, however, the velocity over the rough wall in the inner region (
 $y^{\prime +0}<100$
) then increases and approaches the corresponding final velocity at a much earlier time of
$y^{\prime +0}<100$
) then increases and approaches the corresponding final velocity at a much earlier time of
 $t^{\ast }=4$
.
$t^{\ast }=4$
. -
(8) In contrast to the response of turbulence over a smooth wall, all three components of the r.m.s. of turbulent velocity fluctuations (
 $u_{rms}^{\prime },v_{rms}^{\prime },w_{rms}^{\prime }$
) on the rough wall respond at approximately the same time in the near-wall region, after a short delay. They reach a peak (streamwise component) or approach their final values (wall-normal and spanwise components) shortly after
$u_{rms}^{\prime },v_{rms}^{\prime },w_{rms}^{\prime }$
) on the rough wall respond at approximately the same time in the near-wall region, after a short delay. They reach a peak (streamwise component) or approach their final values (wall-normal and spanwise components) shortly after
 $t^{\ast }=0.8$
. The turbulence defined in such a way begins to move towards the rod-like axisymmetric turbulence state from a very early stage (
$t^{\ast }=0.8$
. The turbulence defined in such a way begins to move towards the rod-like axisymmetric turbulence state from a very early stage (
 $t^{\ast }\sim 0.2$
), confirming similar values of
$t^{\ast }\sim 0.2$
), confirming similar values of
 $v_{rms}^{\prime }$
and
$v_{rms}^{\prime }$
and
 $w_{rms}^{\prime }$
. This is demonstrated in the AIM at the locations within the roughness element and close to the roughness crest. In common with the smooth wall, the development of r.m.s. of velocity fluctuations and turbulent shear stress in the core region exhibits increasing delays with increasing distance from the wall.
$w_{rms}^{\prime }$
. This is demonstrated in the AIM at the locations within the roughness element and close to the roughness crest. In common with the smooth wall, the development of r.m.s. of velocity fluctuations and turbulent shear stress in the core region exhibits increasing delays with increasing distance from the wall. -
(9) The primary vortices generated in the early transient period cause a rapid increase in turbulent shear stress, which strongly overshoots the final values. The passing of vortices over the lee side and forward side of roughness elements during advection downstream causes the shear stress to oscillate in time. Signatures of such variations are found in the wall-normal r.m.s. fluctuation velocity.
-
(10) The influence of the spatial perturbation velocity due to the roughness geometry (known as dispersive or form-induced stress) is significant during the initial transient flow, but largely confined within a region up to
 $y/k_{t}\sim 1.3$
above the roughness crest.
$y/k_{t}\sim 1.3$
above the roughness crest.
Acknowledgements
The authors acknowledge funding from the UK Engineering and Physical Science Research Council (EP/G068925/1 and EP/G069441/1). We are grateful to Professor P. Orlandi for his advice on the numerical methods. This work made use of the facilities of the N8 HPC, provided and funded by the N8 consortium and EPSRC (grant no. EP/K000225/1), as well as the UK National Supercomputer ARCHER sponsored by EPSRC through the UK Turbulence Consortium (UKTC) (grant no. EP/L000261/1).