1. Introduction
The more and more intense exploration of oceanic resources in the past decades makes topical the problem of safety and protection of marine engineering constructions, harbours, gulfs, beaches and ships. Great attention has been paid to the consequences of surface wave impacts, especially those caused by tidal and tsunami waves, as well as swells and wind waves. Internal waves represent another typical kind of wave motion in the oceans, and similarly to the surface waves, they commonly occur in the oceans, seas, lakes and other large-scale estuaries, including artificially constructed storage ponds. They can significantly affect climate change, water mixing, migration of plankton, sediment transport and coastal engineering constructions (platform, oil and gas pipelines, etc.), as well as underwater navigation.
One of the topical problems related to the impact of oceanic waves on the coastal zone is the calculation of wave transformation when waves pass over the continental shelf. This problem has been studied sufficiently well for small-amplitude surface waves passing over the stepwise obstacle. The first entry into the problem was made by Lamb (Reference Lamb1932), who derived simple formulae for the transformation coefficients in the long-wave approximation. The rigorous problem statement for quasi-monochromatic linear waves of arbitrary wavelength was considered then by many authors, starting from the seminal paper by Bartholomeusz (Reference Bartholomeusz1958), who took into account not only travelling waves but also evanescent modes localised in the vicinity of the bottom step edge. The reviews of results obtained can be found, for example, in Massel (Reference Massel1989), Dingemans (Reference Dingemans1997) and Kurkin, Semin & Stepanyants (Reference Kurkin, Semin and Stepanyants2015).
The major outcome of these studies is that exact values of transformation coefficients (the coefficients of transmission and reflection) can be obtained via numerical solution of a set of algebraic equations for the transformation coefficients and coefficients of excitation of evanescent modes. The number of equations required to reach a certain accuracy depends on the depth ratio ![]() $h_2/h_1$, where
$h_2/h_1$, where ![]() $h_1$ is the depth in front of the edge of the bottom step, and
$h_1$ is the depth in front of the edge of the bottom step, and ![]() $h_2$ is the depth behind the edge. When the ratio
$h_2$ is the depth behind the edge. When the ratio ![]() $h_2/h_1$ is too small (say, of the order of
$h_2/h_1$ is too small (say, of the order of ![]() $10^{-2}$) or too big (of the order of
$10^{-2}$) or too big (of the order of ![]() $10^{2}$), the total number of required equations may reach 500. This is, certainly, not handy for practical applications and theoretical analysis of dependences of the transformation coefficients on the parameters. (In reality, such extreme values of depth drops are out of practical interest.) When a high accuracy is not required, the transmission coefficient can be calculated analytically, taking into consideration only travelling modes and neglecting evanescent modes. This idea was suggested by Miles (Reference Miles1967) and realised in Kurkin et al. (Reference Kurkin, Semin and Stepanyants2015), where the corresponding analytical formulae were derived. It was shown by comparison with exact formulae and numerical calculations that the transmission coefficient within such approximations can be obtained with an error less than 5 %, whereas the error of the reflection coefficient is much greater (however, the reflection coefficient is usually not so topical from the practical point of view).
$10^{2}$), the total number of required equations may reach 500. This is, certainly, not handy for practical applications and theoretical analysis of dependences of the transformation coefficients on the parameters. (In reality, such extreme values of depth drops are out of practical interest.) When a high accuracy is not required, the transmission coefficient can be calculated analytically, taking into consideration only travelling modes and neglecting evanescent modes. This idea was suggested by Miles (Reference Miles1967) and realised in Kurkin et al. (Reference Kurkin, Semin and Stepanyants2015), where the corresponding analytical formulae were derived. It was shown by comparison with exact formulae and numerical calculations that the transmission coefficient within such approximations can be obtained with an error less than 5 %, whereas the error of the reflection coefficient is much greater (however, the reflection coefficient is usually not so topical from the practical point of view).
Another heuristic approach was suggested by one of these authors for the approximate calculation of transformation coefficients (Giniyatullin et al. Reference Giniyatullin, Kurkin, Semin and Stepanyants2014; Churaev, Semin & Stepanyants Reference Churaev, Semin and Stepanyants2015; Kurkin et al. Reference Kurkin, Semin and Stepanyants2015; Meylan & Stepanyants Reference Meylan and Stepanyants2024). The idea of this approach is based on the classical Lamb formulae for the transformation coefficients of long surface waves (Lamb Reference Lamb1932) presented in terms of wave speed ratio on both sides of the bottom-step edge ![]() $c_2/c_1$. As shown in the cited papers, very good agreement with the rigorous analytical approach can be achieved if, in the transmission coefficient, the ratio of group speeds
$c_2/c_1$. As shown in the cited papers, very good agreement with the rigorous analytical approach can be achieved if, in the transmission coefficient, the ratio of group speeds ![]() $c_{g2}/c_{g1}$ is used instead of
$c_{g2}/c_{g1}$ is used instead of ![]() $c_2/c_1$, whereas in the reflection coefficient, the ratio of phase speeds
$c_2/c_1$, whereas in the reflection coefficient, the ratio of phase speeds ![]() $c_{p2}/c_{p1}$ is used. This approach has been validated by direct numerical modelling, and it was shown that it is accurate enough, robust, and handy for analysis and application.
$c_{p2}/c_{p1}$ is used. This approach has been validated by direct numerical modelling, and it was shown that it is accurate enough, robust, and handy for analysis and application.
The problem of internal wave transformation on a bottom step has not been studied thus far with the same completeness as for surface waves. The transformation coefficients for internal waves passing over the bottom step in a two-layer fluid were derived only in the shallow-water limit, assuming that the density difference between the layers is small, i.e. in the Boussinesq approximation (Brekhovskikh & Goncharov Reference Brekhovskikh and Goncharov1994; Miropol'sky Reference Miropol'sky2001; Grimshaw, Pelinovsky & Talipova Reference Grimshaw, Pelinovsky and Talipova2008). On the basis of the derived formula, the problem of internal soliton transformation on the bottom step was studied for different polarities of solitons and position of the pycnocline (sharp density interface between the layers) (Maderich et al. Reference Maderich, Talipova, Grimshaw, Pelinovsky, Choi, Brovchenko, Terletska and Kim2009, Reference Maderich, Talipova, Grimshaw, Terletska, Brovchenko, Pelinovsky and Byung2010). For the calculation of transformation coefficients of internal waves of arbitrary wavelength in a two-layer fluid of arbitrary layer densities, only the approximate approach was suggested thus far (Churaev et al. Reference Churaev, Semin and Stepanyants2015). It was demonstrated that the approximate formulae agree well with the numerical data, and can be used for practical applications when high accuracy is not required. However, to our best knowledge, the rigorous approach to the problem of internal wave transformation on a bottom step has not been developed thus far. In this paper, we derive transformation coefficients for linear internal waves in two-layer fluid free from the restriction on wavelength and layer densities. We show that accurate results can be obtained from the solution of an infinite set of algebraic equations for the transformation coefficients of travelling waves and coefficients of excitation of evanescent modes. In practice, the set should be truncated and solved numerically. The number of used equations depends on the required accuracy and hydrological parameters (depth ratio ![]() $h_2/h_1$, density ratio
$h_2/h_1$, density ratio ![]() $\rho _2/\rho _1$, pycnocline depth
$\rho _2/\rho _1$, pycnocline depth ![]() $h_0$, dimensionless wavenumber of an incident wave
$h_0$, dimensionless wavenumber of an incident wave ![]() $\kappa = kh_1$). In the limiting case
$\kappa = kh_1$). In the limiting case ![]() $\rho _2/\rho _1 \to 0$, our results reduce to that for surface waves (see e.g. Massel Reference Massel1989; Kurkin et al. Reference Kurkin, Semin and Stepanyants2015). In another limiting case,
$\rho _2/\rho _1 \to 0$, our results reduce to that for surface waves (see e.g. Massel Reference Massel1989; Kurkin et al. Reference Kurkin, Semin and Stepanyants2015). In another limiting case, ![]() $\rho _2/\rho _1 \to 1$ and
$\rho _2/\rho _1 \to 1$ and ![]() $\kappa \to 0$, our results reduce to the Lamb-type formulae derived in Grimshaw et al. (Reference Grimshaw, Pelinovsky and Talipova2008). We show also that the results derived earlier on the basis of the heuristic approach agree well with the rigorous approach developed here. Data from direct numerical modelling also validate our theoretical results. We also derive the relationship between the transmission and reflection coefficients that constitute the energy flux conservation, and show that the theoretical and numerical data agree well with this law.
$\kappa \to 0$, our results reduce to the Lamb-type formulae derived in Grimshaw et al. (Reference Grimshaw, Pelinovsky and Talipova2008). We show also that the results derived earlier on the basis of the heuristic approach agree well with the rigorous approach developed here. Data from direct numerical modelling also validate our theoretical results. We also derive the relationship between the transmission and reflection coefficients that constitute the energy flux conservation, and show that the theoretical and numerical data agree well with this law.
2. Problem formulation
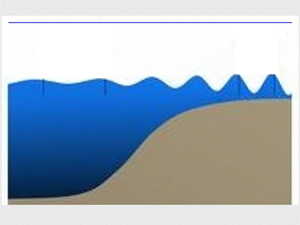
In this section, we formulate the mathematical model, which we employ to describe the transformation of small-amplitude internal gravity waves passing over the underwater obstacle in the form of a bottom step in a two-layer density stratified fluid. The physical model is considered in a two-dimensional Cartesian coordinate system with ![]() $x$-axis along the mean water level at the interface, and
$x$-axis along the mean water level at the interface, and ![]() $z$-axis directed vertically upwards, as exhibited in figure 1. Further, figure 1 illustrates two potential configurations with an incident wave originating either from the deeper region (as seen in figure 1a) or from the shallower region (as depicted in figure 1b). It is assumed that the interface is at the depth
$z$-axis directed vertically upwards, as exhibited in figure 1. Further, figure 1 illustrates two potential configurations with an incident wave originating either from the deeper region (as seen in figure 1a) or from the shallower region (as depicted in figure 1b). It is assumed that the interface is at the depth ![]() $h_0$ from the water surface, whereas the depth of the rigid bottom bed is
$h_0$ from the water surface, whereas the depth of the rigid bottom bed is ![]() $h_j$,
$h_j$, ![]() $j=1,2$ on either side of the bottom step located at
$j=1,2$ on either side of the bottom step located at ![]() $x=0$.
$x=0$.

Figure 1. Sketch of the problem geometry: (a) ![]() $h_2/h_1 < 1$, a wavetrain propagates from the deeper region to the shallower one; (b)
$h_2/h_1 < 1$, a wavetrain propagates from the deeper region to the shallower one; (b) ![]() $h_2/h_1 > 1$, a wavetrain propagates from the shallower region to the deeper one.
$h_2/h_1 > 1$, a wavetrain propagates from the shallower region to the deeper one.
We implement the ‘rigid lid approximation’ at the free surface to effectively filter surface waves (see e.g. Miropol'sky Reference Miropol'sky2001). The fluid is assumed to be inviscid and incompressible, and flow is considered to be irrotational. Additionally, the densities of the upper and lower layers are assumed to be ![]() $\rho _1$ and
$\rho _1$ and ![]() $\rho _2$, respectively, with
$\rho _2$, respectively, with ![]() $a=\rho _1/\rho _2 \leq 1$. Consequently, the velocity potentials exist on both sides of the bottom step, which are introduced as
$a=\rho _1/\rho _2 \leq 1$. Consequently, the velocity potentials exist on both sides of the bottom step, which are introduced as ![]() $\boldsymbol {v}_1 = \boldsymbol {\nabla } \varphi _1$ in the domain
$\boldsymbol {v}_1 = \boldsymbol {\nabla } \varphi _1$ in the domain ![]() $\varOmega _1$ (see figure 1), and
$\varOmega _1$ (see figure 1), and ![]() $\boldsymbol {v}_2 = \boldsymbol {\nabla } \varphi _2$ in the domain
$\boldsymbol {v}_2 = \boldsymbol {\nabla } \varphi _2$ in the domain ![]() $\varOmega _2$. The velocity potentials satisfy the Laplace equation as the governing equation, and are given by
$\varOmega _2$. The velocity potentials satisfy the Laplace equation as the governing equation, and are given by
The rigid lid approximation at the air–water interface and the impermeable rigid bottom bed boundary conditions yield
Further, the linearised continuity conditions for the fluid velocity and pressure along the interface are presented as (Lamb Reference Lamb1932)
 \begin{equation} \left.\begin{gathered} \displaystyle\frac{\partial \eta}{\partial t} = \left.\frac{\partial \phi_i}{\partial z}\right|_{z=0^-} = \left.\frac{\partial \phi_i}{\partial z}\right|_{z=0^+},\\ \displaystyle \left.a \left(g\,\frac{\partial \phi_i}{\partial z} + \frac{\partial^2 \phi_i}{\partial t^2}\right)\right|_{z=0^-} = \left.\left(g\,\frac{\partial \phi_i}{\partial z} + \frac{\partial^2 \phi_i}{\partial t^2}\right)\right|_{z=0^+},\end{gathered}\right\} \quad \mbox{for } i=1,2 , \end{equation}
\begin{equation} \left.\begin{gathered} \displaystyle\frac{\partial \eta}{\partial t} = \left.\frac{\partial \phi_i}{\partial z}\right|_{z=0^-} = \left.\frac{\partial \phi_i}{\partial z}\right|_{z=0^+},\\ \displaystyle \left.a \left(g\,\frac{\partial \phi_i}{\partial z} + \frac{\partial^2 \phi_i}{\partial t^2}\right)\right|_{z=0^-} = \left.\left(g\,\frac{\partial \phi_i}{\partial z} + \frac{\partial^2 \phi_i}{\partial t^2}\right)\right|_{z=0^+},\end{gathered}\right\} \quad \mbox{for } i=1,2 , \end{equation}
where ![]() $g$ is the acceleration due to gravity. Then the continuity of pressure and velocity along the step wall at
$g$ is the acceleration due to gravity. Then the continuity of pressure and velocity along the step wall at ![]() $x=0$ gives
$x=0$ gives
 $$\begin{gather} h_1>h_2\quad\begin{cases} \phi_1(0,z) = \phi_2(0,z) & \mbox{for } -h_2< z< h_0,\\ \phi_{1x}(0,z) = \phi_{2x}(0,z) H\,(z+h_2) & \mbox{for } -h_1< z< h_0, \end{cases} \end{gather}$$
$$\begin{gather} h_1>h_2\quad\begin{cases} \phi_1(0,z) = \phi_2(0,z) & \mbox{for } -h_2< z< h_0,\\ \phi_{1x}(0,z) = \phi_{2x}(0,z) H\,(z+h_2) & \mbox{for } -h_1< z< h_0, \end{cases} \end{gather}$$ $$\begin{gather}h_1< h_2\quad\begin{cases} \phi_1(0,z) = \phi_2(0,z) & \mbox{for } -h_1< z< h_0,\\ \phi_{1x}(0,z)\,H(z+h_1) = \phi_{2x}(0,z) & \mbox{for } -h_2< z< h_0, \end{cases} \end{gather}$$
$$\begin{gather}h_1< h_2\quad\begin{cases} \phi_1(0,z) = \phi_2(0,z) & \mbox{for } -h_1< z< h_0,\\ \phi_{1x}(0,z)\,H(z+h_1) = \phi_{2x}(0,z) & \mbox{for } -h_2< z< h_0, \end{cases} \end{gather}$$
where ![]() $H$ is the Heaviside unit step function.
$H$ is the Heaviside unit step function.
As we study the scattering problem, we assume that in the far-field zone, ![]() $|x| \to \infty$, the boundary conditions are
$|x| \to \infty$, the boundary conditions are
where ![]() $k_{j0}$ for
$k_{j0}$ for ![]() $j=1,2$ are wavenumbers of plane progressive waves in the reflection and transmission zones.
$j=1,2$ are wavenumbers of plane progressive waves in the reflection and transmission zones.
3. Plane wave solution
Let us consider a plane wave travelling on the pycnocline between two layers in a fluid of finite depth. In the linear approximation, the interfacial wave can be presented as ![]() $\eta = A \exp ({\mathrm {i}(k x - \omega t)})$. The associated velocity potential can be presented in each layer in the form (Brekhovskikh & Goncharov Reference Brekhovskikh and Goncharov1994)
$\eta = A \exp ({\mathrm {i}(k x - \omega t)})$. The associated velocity potential can be presented in each layer in the form (Brekhovskikh & Goncharov Reference Brekhovskikh and Goncharov1994)
 \begin{align} \phi = \left\{\!\!\begin{array}{ll} -\mathrm{i}\,\dfrac{A \omega}{k}\,\dfrac{\cosh{k(z-h_0)}}{\sinh{kh_0}}\exp({\mathrm{i}(k x - \omega t)}) & \mbox{for } -\infty< x<\infty, 0< z< h_0,\\[10pt] \mathrm{i}\,\dfrac{A \omega}{k}\,\dfrac{\cosh{k(z+h_j)}}{\sinh{kh_j}}\exp({\mathrm{i}(k x - \omega t)}) & \mbox{for } -\infty< x<\infty, \ -h_j< z<0, \end{array}\right. \end{align}
\begin{align} \phi = \left\{\!\!\begin{array}{ll} -\mathrm{i}\,\dfrac{A \omega}{k}\,\dfrac{\cosh{k(z-h_0)}}{\sinh{kh_0}}\exp({\mathrm{i}(k x - \omega t)}) & \mbox{for } -\infty< x<\infty, 0< z< h_0,\\[10pt] \mathrm{i}\,\dfrac{A \omega}{k}\,\dfrac{\cosh{k(z+h_j)}}{\sinh{kh_j}}\exp({\mathrm{i}(k x - \omega t)}) & \mbox{for } -\infty< x<\infty, \ -h_j< z<0, \end{array}\right. \end{align}
where the wave frequency ![]() $\omega$ is linked with the wavenumber
$\omega$ is linked with the wavenumber ![]() $k_j$ by the dispersion relation
$k_j$ by the dispersion relation
This dispersion relation reduces to the dispersion relation for surface gravity waves if ![]() $a=0$. It is worth mentioning that the dispersion relation (3.2) possesses one positive real root that pertains to the travelling mode, and an infinite number of purely imaginary roots that pertain to evanescent modes, in each region
$a=0$. It is worth mentioning that the dispersion relation (3.2) possesses one positive real root that pertains to the travelling mode, and an infinite number of purely imaginary roots that pertain to evanescent modes, in each region ![]() $\varOmega _1$ and
$\varOmega _1$ and ![]() $\varOmega _2$ shown in figure 1. For such modes, the dispersion relation follows from (3.2) by replacing
$\varOmega _2$ shown in figure 1. For such modes, the dispersion relation follows from (3.2) by replacing ![]() $k_j$ with
$k_j$ with ![]() $\mathrm {i} \gamma_{j}$; then it takes the form
$\mathrm {i} \gamma_{j}$; then it takes the form
4. Method of solution
In this section, we present a complete solution of internal wave scattering by the bottom step in a two-layer fluid in terms of the velocity potential. The velocity potentials are considered as sums of travelling and evanescent modes:
 $$\begin{gather} \phi_1(x,z) = \frac{\mathrm{i}\omega}{k_{10}}\left(A_i \exp({\mathrm{i} k_{10}x }) + A_{r0} \exp({-\mathrm{i} k_{10}x})\right)f_{10} (z) + \sum_{n=1}^\infty \frac{\omega}{\gamma_{1n}}\,A_{rn} \exp({\gamma_{1n}x})\, f_{1n}(z), \end{gather}$$
$$\begin{gather} \phi_1(x,z) = \frac{\mathrm{i}\omega}{k_{10}}\left(A_i \exp({\mathrm{i} k_{10}x }) + A_{r0} \exp({-\mathrm{i} k_{10}x})\right)f_{10} (z) + \sum_{n=1}^\infty \frac{\omega}{\gamma_{1n}}\,A_{rn} \exp({\gamma_{1n}x})\, f_{1n}(z), \end{gather}$$ $$\begin{gather}\phi_2(x,z) = \frac{\mathrm{i}\omega}{k_{20}}\,A_{t0}\,f_{20} (z) \exp({\mathrm{i} k_{20} x }) + \sum_{n=1}^\infty \frac{\omega}{\gamma_{2n}}\,A_{tn} \exp({-\gamma_{2n}x})\,f_{2n} (z), \end{gather}$$
$$\begin{gather}\phi_2(x,z) = \frac{\mathrm{i}\omega}{k_{20}}\,A_{t0}\,f_{20} (z) \exp({\mathrm{i} k_{20} x }) + \sum_{n=1}^\infty \frac{\omega}{\gamma_{2n}}\,A_{tn} \exp({-\gamma_{2n}x})\,f_{2n} (z), \end{gather}$$
where ![]() $A_{rn}$ and
$A_{rn}$ and ![]() $A_{tn}$ for
$A_{tn}$ for ![]() $n=0,1,2,\ldots$ are the unknown amplitudes associated with the reflected and transmitted waves, whereas
$n=0,1,2,\ldots$ are the unknown amplitudes associated with the reflected and transmitted waves, whereas ![]() $A_i$ is known incident wave amplitude. The vertical eigenfunctions
$A_i$ is known incident wave amplitude. The vertical eigenfunctions ![]() $f_{j0}(z)$ are given by (cf. (3.1))
$f_{j0}(z)$ are given by (cf. (3.1))
 \begin{equation} f_{j0}(z) = \left\{\!\!\begin{array}{ll} - \dfrac{\cosh{k_{j0} (z-h_0)}}{\sinh{k_{j0}h_0}} & \mbox{for } 0\leq z < h_0,\\[10pt] \dfrac{\cosh{k_{j0}(z+h_j)}}{\sinh{k_{j0}h_j}} & \mbox{for } -h_j < z < 0, \end{array}\right. \end{equation}
\begin{equation} f_{j0}(z) = \left\{\!\!\begin{array}{ll} - \dfrac{\cosh{k_{j0} (z-h_0)}}{\sinh{k_{j0}h_0}} & \mbox{for } 0\leq z < h_0,\\[10pt] \dfrac{\cosh{k_{j0}(z+h_j)}}{\sinh{k_{j0}h_j}} & \mbox{for } -h_j < z < 0, \end{array}\right. \end{equation}
for ![]() $j=1,2$. The vertical eigenfunctions
$j=1,2$. The vertical eigenfunctions ![]() $f_{jn}$ for
$f_{jn}$ for ![]() $n=1,2,3,\ldots$ can be obtained similarly by replacing the wavenumber
$n=1,2,3,\ldots$ can be obtained similarly by replacing the wavenumber ![]() $k_{jn}$ with
$k_{jn}$ with ![]() $\mathrm {i} \gamma _{jn}$. Substituting (4.1) and (4.2) in (2.5), we get
$\mathrm {i} \gamma _{jn}$. Substituting (4.1) and (4.2) in (2.5), we get
 \begin{equation} \begin{cases} \displaystyle \frac{\mathrm{i}}{k_{10}}\,(1 + R_0)\, f_{10}(z) + \sum_{n=1}^{\infty} \frac{1}{\gamma_{1n}}\,R_n\,f_{1n} (z) & {}\\ \displaystyle\quad= \frac{\mathrm{i}}{k_{20}}\,T_0\,f_{20}(z) +\sum_{n=1}^\infty \frac{1}{\gamma_{2n}}\,T_n\, f_{2n} (z) & \mbox{for } -h_2< z< h_0,\\[12pt] \displaystyle \mathrm{i}(1 - R_0)\,f_{10}(z) + \sum_{n=1}^\infty R_n\,f_{1n}(z) & {}\\ \displaystyle\quad = \left\{\mathrm{i} T_0\,f_{20} (z) - \sum_{n=0}^\infty T_n\,f_{2n} (z)\right\} H(z+h_2) & \mbox{for } -h_1 < z< h_0, \end{cases} \end{equation}
\begin{equation} \begin{cases} \displaystyle \frac{\mathrm{i}}{k_{10}}\,(1 + R_0)\, f_{10}(z) + \sum_{n=1}^{\infty} \frac{1}{\gamma_{1n}}\,R_n\,f_{1n} (z) & {}\\ \displaystyle\quad= \frac{\mathrm{i}}{k_{20}}\,T_0\,f_{20}(z) +\sum_{n=1}^\infty \frac{1}{\gamma_{2n}}\,T_n\, f_{2n} (z) & \mbox{for } -h_2< z< h_0,\\[12pt] \displaystyle \mathrm{i}(1 - R_0)\,f_{10}(z) + \sum_{n=1}^\infty R_n\,f_{1n}(z) & {}\\ \displaystyle\quad = \left\{\mathrm{i} T_0\,f_{20} (z) - \sum_{n=0}^\infty T_n\,f_{2n} (z)\right\} H(z+h_2) & \mbox{for } -h_1 < z< h_0, \end{cases} \end{equation}
where ![]() $R_n = A_{rn}/A_i$ and
$R_n = A_{rn}/A_i$ and ![]() $T_n = A_{tn}/A_i$. Similarly, substituting (4.1) and (4.2) in (2.6) yields
$T_n = A_{tn}/A_i$. Similarly, substituting (4.1) and (4.2) in (2.6) yields
 \begin{equation} \begin{cases} \displaystyle \frac{\mathrm{i}}{k_{10}}\,(1 + R_0)\,f_{10}(z) + \sum_{n=1}^{\infty} \frac{1}{\gamma_{1n}}\,R_n\,f_{1n} (z) & {}\\ \displaystyle\quad = \frac{\mathrm{i}}{k_{20}}\,T_0\,f_{20}(z) +\sum_{n=1}^\infty \frac{1}{\gamma_{2n}}\,T_n\, f_{2n} (z) & \mbox{for } -h_1< z< h_0,\\[12pt] \displaystyle \left\{-(1 - R_0)\,f_{10}(z) + \sum_{n=1}^\infty R_n\,f_{1n}(z)\right\}H(z+h_1) & {}\\ \displaystyle\quad =- T_0\,f_{20} (z) - \sum_{n=0}^\infty T_n\,f_{2n} (z) & \mbox{for } -h_2 < z< h_0. \end{cases} \end{equation}
\begin{equation} \begin{cases} \displaystyle \frac{\mathrm{i}}{k_{10}}\,(1 + R_0)\,f_{10}(z) + \sum_{n=1}^{\infty} \frac{1}{\gamma_{1n}}\,R_n\,f_{1n} (z) & {}\\ \displaystyle\quad = \frac{\mathrm{i}}{k_{20}}\,T_0\,f_{20}(z) +\sum_{n=1}^\infty \frac{1}{\gamma_{2n}}\,T_n\, f_{2n} (z) & \mbox{for } -h_1< z< h_0,\\[12pt] \displaystyle \left\{-(1 - R_0)\,f_{10}(z) + \sum_{n=1}^\infty R_n\,f_{1n}(z)\right\}H(z+h_1) & {}\\ \displaystyle\quad =- T_0\,f_{20} (z) - \sum_{n=0}^\infty T_n\,f_{2n} (z) & \mbox{for } -h_2 < z< h_0. \end{cases} \end{equation}5. Results and discussions
Here, we apply the formulae derived in the previous section to the analysis of transformation coefficients setting the following parameters: ![]() $\rho _2 = 1025\ \textrm {kg}\ \textrm {m}^{-3}$,
$\rho _2 = 1025\ \textrm {kg}\ \textrm {m}^{-3}$, ![]() $g = 9.81\ \textrm {m}\ \textrm {s}^{-2}$ and
$g = 9.81\ \textrm {m}\ \textrm {s}^{-2}$ and ![]() $a = 0.9$, unless otherwise mentioned below. The infinite sums in (A11) and (A12) are truncated to contain a finite number of terms,
$a = 0.9$, unless otherwise mentioned below. The infinite sums in (A11) and (A12) are truncated to contain a finite number of terms, ![]() $N$. A convergence study on transformation coefficients has been made to determine an appropriate number of terms
$N$. A convergence study on transformation coefficients has been made to determine an appropriate number of terms ![]() $N$ for the subsequent analysis.
$N$ for the subsequent analysis.
Tables 1–3 show that ![]() $400$ evanescent modes for
$400$ evanescent modes for ![]() $h_2/h_1 < 1$ and
$h_2/h_1 < 1$ and ![]() $200$ evanescent modes for
$200$ evanescent modes for ![]() $h_2/h_1 > 1$ are quite sufficient to get five decimal places accuracy in the transformation coefficients, irrespective of the ratio of water depths.
$h_2/h_1 > 1$ are quite sufficient to get five decimal places accuracy in the transformation coefficients, irrespective of the ratio of water depths.
Table 1. Convergence study for two different values of ![]() $h_2/h_1$ with
$h_2/h_1$ with ![]() $\kappa = 1$ and
$\kappa = 1$ and ![]() $h_0/h_1 = 0.1$.
$h_0/h_1 = 0.1$.

Table 2. Convergence studies for two different values of ![]() $h_2/h_1$ with
$h_2/h_1$ with ![]() $\kappa = 1$ and
$\kappa = 1$ and ![]() $h_0/h_1 = 1$.
$h_0/h_1 = 1$.

Table 3. Convergence studies for two different values of ![]() $h_2/h_1$ with
$h_2/h_1$ with ![]() $\kappa = 1$ and
$\kappa = 1$ and ![]() $h_0/h_1 = 10$.
$h_0/h_1 = 10$.

Figure 2 demonstrates the variations of the reflection and transmission coefficients as functions of the water depth ratio ![]() $h_2/h_1$ (
$h_2/h_1$ (![]() $0.01 < h_2/h_1 < 100$) for different values of dimensionless wavenumber
$0.01 < h_2/h_1 < 100$) for different values of dimensionless wavenumber ![]() $\kappa = kh_1$ with
$\kappa = kh_1$ with ![]() $h_0/h_1 = 0.1$. It shows that a significant amount of wave energy is reflected and transmitted when
$h_0/h_1 = 0.1$. It shows that a significant amount of wave energy is reflected and transmitted when ![]() $h_2/h_1 < 1$. Besides, the transmission coefficient
$h_2/h_1 < 1$. Besides, the transmission coefficient ![]() $K_t$ is greater than 1 for certain values of
$K_t$ is greater than 1 for certain values of ![]() $h_2/h_1 < 1$, irrespective of the values of
$h_2/h_1 < 1$, irrespective of the values of ![]() $\kappa$. However, for large values of
$\kappa$. However, for large values of ![]() $\kappa$, e.g. for
$\kappa$, e.g. for ![]() $\kappa = 10$, the transmission coefficient is a non-monotonic function of depth ratio in the range
$\kappa = 10$, the transmission coefficient is a non-monotonic function of depth ratio in the range ![]() $h_2/h_1 < 1$. This phenomenon has been revealed both for surface (Kurkin et al. Reference Kurkin, Semin and Stepanyants2015) and internal (Churaev et al. Reference Churaev, Semin and Stepanyants2015) waves. In figure 2, we present the reflection and transmission coefficients obtained both within the current study and with the help of approximate formulae proposed in Churaev et al. (Reference Churaev, Semin and Stepanyants2015) for
$h_2/h_1 < 1$. This phenomenon has been revealed both for surface (Kurkin et al. Reference Kurkin, Semin and Stepanyants2015) and internal (Churaev et al. Reference Churaev, Semin and Stepanyants2015) waves. In figure 2, we present the reflection and transmission coefficients obtained both within the current study and with the help of approximate formulae proposed in Churaev et al. (Reference Churaev, Semin and Stepanyants2015) for ![]() $a = 0.9961$. Some discrepancies between the data can be explained by the influence of the non-Boussinesq effect in our case with
$a = 0.9961$. Some discrepancies between the data can be explained by the influence of the non-Boussinesq effect in our case with ![]() $a = 0.9$.
$a = 0.9$.

Figure 2. Variations of the reflection coefficient ![]() $K_r$ and transmission coefficient
$K_r$ and transmission coefficient ![]() $K_t$ for different values of the dimensionless wavenumber
$K_t$ for different values of the dimensionless wavenumber ![]() $\kappa$ for
$\kappa$ for ![]() $h_0/h_1 = 0.1$ and
$h_0/h_1 = 0.1$ and ![]() $a = 0.9$. Colour dots show the results derived with the help of the approximate formulae proposed in Churaev et al. (Reference Churaev, Semin and Stepanyants2015) for
$a = 0.9$. Colour dots show the results derived with the help of the approximate formulae proposed in Churaev et al. (Reference Churaev, Semin and Stepanyants2015) for ![]() $a = 0.9961$.
$a = 0.9961$.
For ![]() $h_2/h_1 > 1$, the reflection coefficient
$h_2/h_1 > 1$, the reflection coefficient ![]() $K_r$ is close to zero, consequently the transmission coefficient is close to unity for
$K_r$ is close to zero, consequently the transmission coefficient is close to unity for ![]() $\kappa = 0.1$,
$\kappa = 0.1$, ![]() $1$ and
$1$ and ![]() $10$.
$10$.
The importance of evanescent modes in the scattering phenomenon has been mentioned in the literature; their role in the scattering of surface gravity waves in a homogeneous fluid was studied in Kurkin et al. (Reference Kurkin, Semin and Stepanyants2015). In figure 3, we show excitation coefficients ![]() $A_{rj}/A_{i}$, for
$A_{rj}/A_{i}$, for ![]() $j=1,\ldots,5$, of the first five evanescent wave modes that appear on the left from the bottom step edge for three values of
$j=1,\ldots,5$, of the first five evanescent wave modes that appear on the left from the bottom step edge for three values of ![]() $\kappa$ as functions of the depth ratio
$\kappa$ as functions of the depth ratio ![]() $h_2/h_1$. Figure 3 reveals that the excitation coefficients, being rather small, attain maxima for certain values of
$h_2/h_1$. Figure 3 reveals that the excitation coefficients, being rather small, attain maxima for certain values of ![]() $h_2/h_1 < 1$. The role of higher-order evanescent modes hardly becomes visible regardless of the thickness of the lower layer
$h_2/h_1 < 1$. The role of higher-order evanescent modes hardly becomes visible regardless of the thickness of the lower layer ![]() $h_2$. Noticeably, the coefficients
$h_2$. Noticeably, the coefficients ![]() $A_{rj}/A_i$,
$A_{rj}/A_i$, ![]() $j=1,\ldots, 5$, possess multiple zero minima with maxima in the interim for
$j=1,\ldots, 5$, possess multiple zero minima with maxima in the interim for ![]() $h_2/h_1 < 1$; then they smoothly approach small constant values when
$h_2/h_1 < 1$; then they smoothly approach small constant values when ![]() $h_2/h_1$ becomes greater than 1. As follows from figure 3, the dependence of excitation coefficients
$h_2/h_1$ becomes greater than 1. As follows from figure 3, the dependence of excitation coefficients ![]() $A_{rj}/A_i$ on
$A_{rj}/A_i$ on ![]() $h_2/h_1$ qualitatively is the same for all three values of
$h_2/h_1$ qualitatively is the same for all three values of ![]() $\kappa$. However, their values at
$\kappa$. However, their values at ![]() $\kappa = 1$ are much greater than at
$\kappa = 1$ are much greater than at ![]() $\kappa = 0.1$ or at
$\kappa = 0.1$ or at ![]() $\kappa = 10$. In all cases, the amplitude of the first evanescent mode
$\kappa = 10$. In all cases, the amplitude of the first evanescent mode ![]() $A_{r1}/A_i$ is noticeably greater than amplitudes of other evanescent modes with
$A_{r1}/A_i$ is noticeably greater than amplitudes of other evanescent modes with ![]() $j > 1$. This supports Miles’ idea (Miles Reference Miles1967) that the first evanescent mode plays a dominant role, and transformation coefficients can be evaluated with an acceptable accuracy by using only one first evanescent mode in the sums of (A11) and (A12). This idea was realised in Kurkin et al. (Reference Kurkin, Semin and Stepanyants2015).
$j > 1$. This supports Miles’ idea (Miles Reference Miles1967) that the first evanescent mode plays a dominant role, and transformation coefficients can be evaluated with an acceptable accuracy by using only one first evanescent mode in the sums of (A11) and (A12). This idea was realised in Kurkin et al. (Reference Kurkin, Semin and Stepanyants2015).

Figure 3. Variations of the first six excitation coefficients associated with the reflected wave amplitudes ![]() $A_{rj}/A_i$,
$A_{rj}/A_i$, ![]() $j=1,2,\ldots,5$, versus depth ratio
$j=1,2,\ldots,5$, versus depth ratio ![]() $h_2/h_1$ for different values of dimensionless wavenumber
$h_2/h_1$ for different values of dimensionless wavenumber ![]() $\kappa$ for
$\kappa$ for ![]() $h_0/h_1 = 0.1$: (a)
$h_0/h_1 = 0.1$: (a) ![]() $\kappa = 0.1$, (b)
$\kappa = 0.1$, (b) ![]() $\kappa = 1$, (c)
$\kappa = 1$, (c) ![]() $\kappa = 10$.
$\kappa = 10$.
Figures 4 and 5, as well as figures 6 and 7, show the same dependences as in figures 2 and 3 but for ![]() $h_0/h_1 = 1$ and
$h_0/h_1 = 1$ and ![]() $h_0/h_1 = 10$, respectively. However, the reflection and transmission coefficients become greater in the range
$h_0/h_1 = 10$, respectively. However, the reflection and transmission coefficients become greater in the range ![]() $h_2/h_1<1$ when the ratio
$h_2/h_1<1$ when the ratio ![]() $h_0/h_1$ increases. A simultaneous increase of the reflection and transmission coefficients does not contradict the energy flux conservation because the increase in wave amplitude is accompanied by a decrease in the wavelength.
$h_0/h_1$ increases. A simultaneous increase of the reflection and transmission coefficients does not contradict the energy flux conservation because the increase in wave amplitude is accompanied by a decrease in the wavelength.

Figure 4. The same as in figure 2 but for ![]() $h_0/h_1 = 1$.
$h_0/h_1 = 1$.

Figure 5. The same as in figure 3 but for ![]() $h_0/h_1 = 1$: (a)
$h_0/h_1 = 1$: (a) ![]() $\kappa = 0.1$, (b)
$\kappa = 0.1$, (b) ![]() $\kappa = 1$, (c)
$\kappa = 1$, (c) ![]() $\kappa = 10$.
$\kappa = 10$.

Figure 6. The same as in figure 2 but for ![]() $h_0/h_1 = 10$.
$h_0/h_1 = 10$.

Figure 7. The same as in figure 3 but for ![]() $h_0/h_1 = 10$: (a)
$h_0/h_1 = 10$: (a) ![]() $\kappa = 0.1$, (b)
$\kappa = 0.1$, (b) ![]() $\kappa = 1$, (c)
$\kappa = 1$, (c) ![]() $\kappa = 10$.
$\kappa = 10$.
One can notice that fewer numbers of zero minima and maxima occur for ![]() $h_2/h_1 < 1$ when
$h_2/h_1 < 1$ when ![]() $h_0/h_1$ increases from
$h_0/h_1$ increases from ![]() $0.1$ to
$0.1$ to ![]() $10$.
$10$.
Noticeably, figures 2, 4 and 6 show that practically complete wave transmission occurs when ![]() $h_2/h_1$ becomes greater than unity, regardless of the depth of the interface from the rigid surface
$h_2/h_1$ becomes greater than unity, regardless of the depth of the interface from the rigid surface ![]() $h_0$. When the pycnocline position becomes closer to the bottom so that
$h_0$. When the pycnocline position becomes closer to the bottom so that ![]() $h_0/h_1$ is too big, and the depth ratio
$h_0/h_1$ is too big, and the depth ratio ![]() $h_2/h_1$ is too small, a numerical solution of the systems (A11) and (A12) becomes difficult and even impossible. Apparently, this happens because the main matrix of the system becomes ill-conditioned. In particular, we were unable to obtain a numerical solution for
$h_2/h_1$ is too small, a numerical solution of the systems (A11) and (A12) becomes difficult and even impossible. Apparently, this happens because the main matrix of the system becomes ill-conditioned. In particular, we were unable to obtain a numerical solution for ![]() $h_0/h_1 = 10$ when
$h_0/h_1 = 10$ when ![]() $\kappa = 10$ and
$\kappa = 10$ and ![]() $h_2/h_1 < 0.03$ (see figure 6). Apparently, a more advanced asymptotic analysis is needed to get solutions for small and large depth ratios. Note that the approximate formulae derived in Churaev et al. (Reference Churaev, Semin and Stepanyants2015) are in good agreement with the analytical formulae developed here for
$h_2/h_1 < 0.03$ (see figure 6). Apparently, a more advanced asymptotic analysis is needed to get solutions for small and large depth ratios. Note that the approximate formulae derived in Churaev et al. (Reference Churaev, Semin and Stepanyants2015) are in good agreement with the analytical formulae developed here for ![]() $h_2/h_1>1$, irrespective of the pycnocline position and non-dimensional wavenumber.
$h_2/h_1>1$, irrespective of the pycnocline position and non-dimensional wavenumber.
It is interesting to note that while the first evanescent mode with the coefficient ![]() $A_{r1}$ predominates in figures 7(a) and 7(b) for
$A_{r1}$ predominates in figures 7(a) and 7(b) for ![]() $\kappa = 0.1$ and
$\kappa = 0.1$ and ![]() $\kappa = 1$ when
$\kappa = 1$ when ![]() $h_2/h_1 < 1$, the second evanescent mode with the coefficient
$h_2/h_1 < 1$, the second evanescent mode with the coefficient ![]() $A_{r2}$ predominates in figure 7(c) for
$A_{r2}$ predominates in figure 7(c) for ![]() $kh_0 = 10$. Note that for small
$kh_0 = 10$. Note that for small ![]() $h_2/h_1$, the excitation coefficient of the third mode becomes predominant in the case of deep-water waves shown in figures 5(c) and 7(c). Figures 3, 5 and 7 provide an estimate of considering a higher number of evanescent modes to obtain the transformation coefficients for a given accuracy. It may be noted that in Churaev et al. (Reference Churaev, Semin and Stepanyants2015), the authors studied the transformation problem on the basis of the heuristic formula leaving aside the evanescent modes.
$h_2/h_1$, the excitation coefficient of the third mode becomes predominant in the case of deep-water waves shown in figures 5(c) and 7(c). Figures 3, 5 and 7 provide an estimate of considering a higher number of evanescent modes to obtain the transformation coefficients for a given accuracy. It may be noted that in Churaev et al. (Reference Churaev, Semin and Stepanyants2015), the authors studied the transformation problem on the basis of the heuristic formula leaving aside the evanescent modes.
Figures 8–10 demonstrate the influence of the density ratio ![]() $a = \rho _1/\rho _2$ on the reflection and transmission coefficients for different values of the depth ratio
$a = \rho _1/\rho _2$ on the reflection and transmission coefficients for different values of the depth ratio ![]() $h_0/h_1$ with
$h_0/h_1$ with ![]() $\kappa = 1$. Qualitatively, the shown dependences are similar: the smaller the parameter
$\kappa = 1$. Qualitatively, the shown dependences are similar: the smaller the parameter ![]() $a$, the bigger the transmission coefficient and the smaller the reflection coefficient. The influence of this parameter is noticeable only for
$a$, the bigger the transmission coefficient and the smaller the reflection coefficient. The influence of this parameter is noticeable only for ![]() $h_2/h_1 < 1$. The analysis of these three figures reveals that the reflection coefficient
$h_2/h_1 < 1$. The analysis of these three figures reveals that the reflection coefficient ![]() $K_r$ has a minimum that can be zero not only at
$K_r$ has a minimum that can be zero not only at ![]() $h_2/h_1 = 1$. In particular,
$h_2/h_1 = 1$. In particular, ![]() $K_r = 0$ at
$K_r = 0$ at ![]() $h_2/h_1 \approx 0.15$ in the case
$h_2/h_1 \approx 0.15$ in the case ![]() $a = 0.4$ (see figure 8). Positions of secondary minima depend on the relative depth of a pycnocline that is characterised by the parameter
$a = 0.4$ (see figure 8). Positions of secondary minima depend on the relative depth of a pycnocline that is characterised by the parameter ![]() $h_2/h_1$; minima of
$h_2/h_1$; minima of ![]() $K_r$ can occur at
$K_r$ can occur at ![]() $h_2/h_1 > 1$ as illustrated by figures 9 and 10.
$h_2/h_1 > 1$ as illustrated by figures 9 and 10.

Figure 8. Influence of the density ratio ![]() $a$ on transmission coefficients
$a$ on transmission coefficients ![]() $K_r$ and
$K_r$ and ![]() $K_t$ for
$K_t$ for ![]() $h_0/h_1 = 0.1$ and
$h_0/h_1 = 0.1$ and ![]() $\kappa = 1$.
$\kappa = 1$.

Figure 9. The same as in figure 8 but with ![]() $h_0/h_1 = 1$.
$h_0/h_1 = 1$.

Figure 10. The same as in figure 8 but with ![]() $h_0/h_1 = 10$.
$h_0/h_1 = 10$.
To conclude this section, we mention that in all calculations presented above, the quantity ![]() $F$ defined in (A22) was indistinguishable from 1 up to the numerical accuracy.
$F$ defined in (A22) was indistinguishable from 1 up to the numerical accuracy.
6. Concluding remarks
In this paper, we have addressed a gap in the derivation of transformation coefficients for internal waves in a two-layer fluid due to scattering on the underwater step. This study extends earlier known results (Grimshaw et al. Reference Grimshaw, Pelinovsky and Talipova2008) for long internal waves in a two-layer fluid. For fluid of arbitrary depth and density ratio, we have derived an infinite set of equations for the transmission and reflection coefficients, as well as for the excitation coefficients of evanescent modes localised on both sides of the bottom step edge. This set of equations was solved numerically after truncation with a finite number ![]() $N$ of equations. The number of equations in our calculations attained
$N$ of equations. The number of equations in our calculations attained ![]() $N = 450$ (see table 2), but in fact can be much fewer because the amplitudes of evanescent modes quickly decrease with mode number. We presented the analysis of transformation coefficients for the different dimensionless wavenumbers of an incident wave
$N = 450$ (see table 2), but in fact can be much fewer because the amplitudes of evanescent modes quickly decrease with mode number. We presented the analysis of transformation coefficients for the different dimensionless wavenumbers of an incident wave ![]() $\kappa = kh_1$, different relative depths of a pycnocline
$\kappa = kh_1$, different relative depths of a pycnocline ![]() $h_0/h_1$, and different values of the density ratio
$h_0/h_1$, and different values of the density ratio ![]() $a = \rho _1/\rho _2$. We have derived the relationship between the transmission and reflection coefficients that constitute the energy flux conservation, and show that the theoretical and numerical data agree well with this law; this can be considered as an independent validation of the results obtained. In such fullness, the problem of internal wave transformation on a bottom step has not been studied thus far even in the linear approximation.
$a = \rho _1/\rho _2$. We have derived the relationship between the transmission and reflection coefficients that constitute the energy flux conservation, and show that the theoretical and numerical data agree well with this law; this can be considered as an independent validation of the results obtained. In such fullness, the problem of internal wave transformation on a bottom step has not been studied thus far even in the linear approximation.
The constructed transformation coefficients and their dependences on parameters agree well with earlier obtained results of the direct numerical modelling of internal wave transformation and approximate heuristic formulae (Churaev et al. Reference Churaev, Semin and Stepanyants2015), as well as with the results obtained for surface waves in a homogeneous fluid (Kurkin et al. Reference Kurkin, Semin and Stepanyants2015). We have also demonstrated that Miles’ idea (Miles Reference Miles1967) to use only one first evanescent mode to calculate the transformation coefficients analytically can be quite acceptable when high accuracy is not required. However, an important question on the character of amplitude decay of evanescent modes with the mode number remains open; this can be a matter for a separate study.
It is worthwhile mentioning that the derived formulae are free from the Boussinesq approximation and can be used for any density ratio ![]() $a = \rho _1/\rho _2$ of fluid layers. Such situations when the Boussinesq approximation becomes inapplicable can be met in some technological processes where fluids of different densities are considered. Other examples can occur in oceans. As is well known, nowadays oil spill accidents rather often occur in oceans leading to the two-layer oil–water fluid with density ratio
$a = \rho _1/\rho _2$ of fluid layers. Such situations when the Boussinesq approximation becomes inapplicable can be met in some technological processes where fluids of different densities are considered. Other examples can occur in oceans. As is well known, nowadays oil spill accidents rather often occur in oceans leading to the two-layer oil–water fluid with density ratio ![]() $\rho _1/\rho _2 \approx 0.8\unicode{x2013} 0.9$. Another example when the Boussinesq approximation becomes inapplicable is the interface between clean water overlaying a mud layer near the bottom with a big density difference between the layers.
$\rho _1/\rho _2 \approx 0.8\unicode{x2013} 0.9$. Another example when the Boussinesq approximation becomes inapplicable is the interface between clean water overlaying a mud layer near the bottom with a big density difference between the layers.
Further development of the results obtained can be associated with the influence of nonlinearity on wave transformation. The nonlinear effects in the internal solitary wave transformation on a bottom step were studied in Grimshaw et al. (Reference Grimshaw, Pelinovsky and Talipova2008) and Maderich et al. (Reference Maderich, Talipova, Grimshaw, Pelinovsky, Choi, Brovchenko, Terletska and Kim2009, Reference Maderich, Talipova, Grimshaw, Terletska, Brovchenko, Pelinovsky and Byung2010) in the long-wave approximation. It is also a matter of interest to consider a transformation of internal envelope solitons and breathers on the underwater step similar to what was considered for surface waves (Ducrozet, Slunyaev & Stepanyants Reference Ducrozet, Slunyaev and Stepanyants2021).
We have studied here a model problem of wave transformation on the stepwise bottom topography with sharp change of the depth. In the opposite limit when the topography is smooth compared to the wavelength, the traditional WKB approximation can be used. For some particular bottom profiles, exact solutions can be obtained (see e.g. Churilov & Stepanyants (Reference Churilov and Stepanyants2022a,Reference Churilov and Stepanyantsb) and references therein).
Acknowledgements
The authors are thankful to S. Semin for his contribution to this paper at an early stage of the work. They are also thankful to T. Sahoo for his interest in this work and support.
Funding
S.B. acknowledges financial support provided by the National Natural Science Foundation of China via grant nos W2433140, 52192693, 52192690, 52371270, U20A20327, 52350410468. Y.S. acknowledges financial support provided by the Ministry of Science and Higher Education of the Russian Federation via grant no. FSWE-2023-0004.
Declaration of interests
The authors declare no conflict of interests.
Appendix. Numerical determining of the transformation coefficients and coefficients of evanescent mode excitation
Equations (4.4) and (4.5) represent an infinite system of equations with an infinite number of unknowns, which include the reflected and transmitted wave amplitudes ![]() $R_0$ and
$R_0$ and ![]() $T_0$, respectively, and coefficients of excitation of evanescent modes
$T_0$, respectively, and coefficients of excitation of evanescent modes ![]() $R_n$ and
$R_n$ and ![]() $T_n$ for
$T_n$ for ![]() $n \geq 1$. The approach for resolving such systems was outlined initially in the seminal work of Takano (Reference Takano1960), and subsequently adapted to solutions of similar problems (see e.g. Takano Reference Takano1967; Massel Reference Massel1989; Dingemans Reference Dingemans1997; Kurkin et al. Reference Kurkin, Semin and Stepanyants2015; Meylan & Stepanyants Reference Meylan and Stepanyants2024). Employing this methodology, we integrate each equation over the vertical coordinate
$n \geq 1$. The approach for resolving such systems was outlined initially in the seminal work of Takano (Reference Takano1960), and subsequently adapted to solutions of similar problems (see e.g. Takano Reference Takano1967; Massel Reference Massel1989; Dingemans Reference Dingemans1997; Kurkin et al. Reference Kurkin, Semin and Stepanyants2015; Meylan & Stepanyants Reference Meylan and Stepanyants2024). Employing this methodology, we integrate each equation over the vertical coordinate ![]() $z$ from the bottom to the rigid lid, incorporating appropriately selected weights from the vertical eigenfunctions denoted as
$z$ from the bottom to the rigid lid, incorporating appropriately selected weights from the vertical eigenfunctions denoted as ![]() $f_{jn} (z)$.
$f_{jn} (z)$.
The methodology proposed by Takano (Reference Takano1960) involves a sequence of orthogonal functions appropriate for the dispersion characteristics of surface gravity waves. However, this framework does not hold for internal gravity waves. Therefore, we integrate the system (2.5) over ![]() $z$ with suitably chosen weight functions:
$z$ with suitably chosen weight functions:
 \begin{equation} h_1>h_2\quad \begin{cases} \displaystyle \int_{-h_2}^{h_0}\phi_1(0,z)\,f_{2m} (z) \,{\rm d}z= \int_{-h_2}^{h_0} \phi_2(0,z)\,f_{2m}(z) \,{\rm d}z,\\[12pt] \displaystyle \int_{-h_1}^{h_0} \phi_{1x}(0,z)\,f_{1m} (z) \,{\rm d}z= \int_{-h_1}^{h_0} \phi_{2x}(0,z)\,f_{1m}(z)\,H(z+h_2) \,{\rm d}z. \end{cases} \end{equation}
\begin{equation} h_1>h_2\quad \begin{cases} \displaystyle \int_{-h_2}^{h_0}\phi_1(0,z)\,f_{2m} (z) \,{\rm d}z= \int_{-h_2}^{h_0} \phi_2(0,z)\,f_{2m}(z) \,{\rm d}z,\\[12pt] \displaystyle \int_{-h_1}^{h_0} \phi_{1x}(0,z)\,f_{1m} (z) \,{\rm d}z= \int_{-h_1}^{h_0} \phi_{2x}(0,z)\,f_{1m}(z)\,H(z+h_2) \,{\rm d}z. \end{cases} \end{equation}Similarly, we integrate the system (2.6):
 \begin{equation} h_1< h_2\quad \begin{cases} \displaystyle \int_{-h_1}^{h_0}\phi_1(0,z)\,f_{1m}(z) \,{\rm d}z = \int_{-h_1}^{h_0}\phi_2(0,z)\,f_{1m}(z) \,{\rm d}z,\\[12pt] \displaystyle \int_{-h_2}^{h_0}\phi_{1x}(0,z)\,f_{2m}(z)\,H(z+h_1) \,{\rm d}z = \int_{-h_2}^{h_0} \phi_{2x}(0,z)\,f_{2m}(z) \,{\rm d}z. \end{cases} \end{equation}
\begin{equation} h_1< h_2\quad \begin{cases} \displaystyle \int_{-h_1}^{h_0}\phi_1(0,z)\,f_{1m}(z) \,{\rm d}z = \int_{-h_1}^{h_0}\phi_2(0,z)\,f_{1m}(z) \,{\rm d}z,\\[12pt] \displaystyle \int_{-h_2}^{h_0}\phi_{1x}(0,z)\,f_{2m}(z)\,H(z+h_1) \,{\rm d}z = \int_{-h_2}^{h_0} \phi_{2x}(0,z)\,f_{2m}(z) \,{\rm d}z. \end{cases} \end{equation}Using (4.1) and (4.4), and taking into account the Heaviside functions that shift the limits of integration, (A1) is rewritten as
 \begin{align} &\frac{\mathrm{i}}{k_{10}} (1+R_{0}) \left[\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}\,{\rm d}z \right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0} \frac{\cosh{k_{10}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{10}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z\vphantom{\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]\nonumber\\ &\qquad + \sum_{n=1}^\infty \frac{1}{k_{1n}}\,R_n \left[\int_{-h_2}^0 \frac{\cosh{k_{1n}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{1n}h_1}\sinh{k_{2m}h_2}}\,{\rm d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0} \frac{\cosh{k_{1n}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z\vphantom{\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right] \nonumber\\ &\quad = \frac{\mathrm{i}}{k_{20}}\,T_0 \left[\int_{-h_2}^0 \frac{\cosh{k_{20}}(z+h_2) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{20}h_2}\sinh{k_{2m}h_2}}\,{\rm d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0} \frac{\cosh{k_{20}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{20}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z\vphantom{\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]\nonumber\\ &\qquad + \sum_{n=1}^\infty \frac{1}{k_{2n}}\,T_n \left[\int_{-h_2}^0 \frac{\cosh{k_{2n}}(z+h_2) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{2n}h_2}\sinh{k_{2m}h_2}}\,{\rm d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0} \frac{\cosh{k_{2n}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z\vphantom{\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right] \end{align}
\begin{align} &\frac{\mathrm{i}}{k_{10}} (1+R_{0}) \left[\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}\,{\rm d}z \right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0} \frac{\cosh{k_{10}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{10}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z\vphantom{\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]\nonumber\\ &\qquad + \sum_{n=1}^\infty \frac{1}{k_{1n}}\,R_n \left[\int_{-h_2}^0 \frac{\cosh{k_{1n}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{1n}h_1}\sinh{k_{2m}h_2}}\,{\rm d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0} \frac{\cosh{k_{1n}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z\vphantom{\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right] \nonumber\\ &\quad = \frac{\mathrm{i}}{k_{20}}\,T_0 \left[\int_{-h_2}^0 \frac{\cosh{k_{20}}(z+h_2) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{20}h_2}\sinh{k_{2m}h_2}}\,{\rm d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0} \frac{\cosh{k_{20}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{20}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z\vphantom{\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]\nonumber\\ &\qquad + \sum_{n=1}^\infty \frac{1}{k_{2n}}\,T_n \left[\int_{-h_2}^0 \frac{\cosh{k_{2n}}(z+h_2) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{2n}h_2}\sinh{k_{2m}h_2}}\,{\rm d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0} \frac{\cosh{k_{2n}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z\vphantom{\int_{-h_2}^0 \frac{\cosh{k_{10}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right] \end{align}and
 \begin{align} & - (1-R_{0})
\left[\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{10}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{10}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]\nonumber\\
&\qquad + \sum_{n=1}^\infty R_n \left[\int_{-h_1}^0
\frac{\cosh{k_{1n}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{1n}h_1}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{1n}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]
\nonumber\\ &\quad =- T_0 \left[\int_{-h_2}^0
\frac{\cosh{k_{20}}(z+h_2)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{20}h_2}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{20}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{20}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right] \nonumber\\
&\qquad - \sum_{n=1}^\infty T_n \left[\int_{-h_2}^0
\frac{\cosh{k_{2n}}(z+h_2)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{2n}h_2}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad\left.{}+ \int_0^{h_0}
\frac{\cosh{k_{2n}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right].
\end{align}
\begin{align} & - (1-R_{0})
\left[\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{10}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{10}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]\nonumber\\
&\qquad + \sum_{n=1}^\infty R_n \left[\int_{-h_1}^0
\frac{\cosh{k_{1n}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{1n}h_1}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{1n}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]
\nonumber\\ &\quad =- T_0 \left[\int_{-h_2}^0
\frac{\cosh{k_{20}}(z+h_2)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{20}h_2}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{20}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{20}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right] \nonumber\\
&\qquad - \sum_{n=1}^\infty T_n \left[\int_{-h_2}^0
\frac{\cosh{k_{2n}}(z+h_2)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{2n}h_2}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad\left.{}+ \int_0^{h_0}
\frac{\cosh{k_{2n}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right].
\end{align}Similarly, using (4.1) and (4.4), (A2) can be rewritten as
 \begin{align}
&\frac{\mathrm{i}}{k_{10}}\,(1+R_{0}) \left[\int_{-h_1}^0
\frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{10}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{10}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]\nonumber\\
& \qquad + \sum_{n=1}^\infty \frac{1}{k_{1n}}\,R_n
\left[\int_{-h_1}^0 \frac{\cosh{k_{1n}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{1n}h_1}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad\left.{}+ \int_0^{h_0}
\frac{\cosh{k_{1n}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]\nonumber\\
&\quad = \frac{\mathrm{i}}{k_{20}}\,T_0 \left[\int_{-h_1}^0
\frac{\cosh{k_{20}}(z+h_2)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{20}h_2}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{20}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{20}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]\nonumber\\
&\qquad + \sum_{n=1}^\infty \frac{1}{k_{2n}}\,T_n
\left[\int_{-h_1}^0 \frac{\cosh{k_{2n}}(z+h_2)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{2n}h_2}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{2n}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]
\end{align}
\begin{align}
&\frac{\mathrm{i}}{k_{10}}\,(1+R_{0}) \left[\int_{-h_1}^0
\frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{10}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{10}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]\nonumber\\
& \qquad + \sum_{n=1}^\infty \frac{1}{k_{1n}}\,R_n
\left[\int_{-h_1}^0 \frac{\cosh{k_{1n}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{1n}h_1}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad\left.{}+ \int_0^{h_0}
\frac{\cosh{k_{1n}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]\nonumber\\
&\quad = \frac{\mathrm{i}}{k_{20}}\,T_0 \left[\int_{-h_1}^0
\frac{\cosh{k_{20}}(z+h_2)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{20}h_2}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{20}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{20}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]\nonumber\\
&\qquad + \sum_{n=1}^\infty \frac{1}{k_{2n}}\,T_n
\left[\int_{-h_1}^0 \frac{\cosh{k_{2n}}(z+h_2)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{2n}h_2}\sinh{k_{1m}h_1}}\,{\rm
d}z\right.\nonumber\\ &\qquad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{2n}(z-h_0)}
\cosh{k_{1m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{1m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{1m}(z+h_1)}}{\sinh{k_{10}h_1}\sinh{k_{1m}h_1}}}\right]
\end{align}and
 \begin{align} & - (1-R_{0})
\left[\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}\,{\rm
d}z\right.\nonumber\\ &\quad\quad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{10}(z-h_0)}
\cosh{k_{2m}(z-h_0)}}{\sinh{k_{10}h_0}\sinh{k_{2m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]\nonumber\\
&\quad\quad + \sum_{n=1}^\infty R_n \left[\int_{-h_1}^0
\frac{\cosh{k_{1n}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{1n}h_1}\sinh{k_{2m}h_2}}\,{\rm
d}z\right.\nonumber\\ &\quad\quad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{1n}(z-h_0)}
\cosh{k_{2m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{2m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]
\nonumber\\ & =- T_0 \left[\int_{-h_2}^0
\frac{\cosh{k_{20}}(z+h_2)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{20}h_2}\sinh{k_{2m}h_2}}\,{\rm
d}z\right.\nonumber\\ &\quad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{20}(z-h_0)}
\cosh{k_{2m}(z-h_0)}}{\sinh{k_{20}h_0}\sinh{k_{2m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]\nonumber\\
&\quad - \sum_{n=1}^\infty T_n \left[\int_{-h_2}^0
\frac{\cosh{k_{2n}}(z+h_2)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{2n}h_2}\sinh{k_{2m}h_2}}\,{\rm
d}z\right.\nonumber\\ &\quad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{2n}(z-h_0)}
\cosh{k_{2m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{2m}h_0}}{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right].
\end{align}
\begin{align} & - (1-R_{0})
\left[\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}\,{\rm
d}z\right.\nonumber\\ &\quad\quad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{10}(z-h_0)}
\cosh{k_{2m}(z-h_0)}}{\sinh{k_{10}h_0}\sinh{k_{2m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]\nonumber\\
&\quad\quad + \sum_{n=1}^\infty R_n \left[\int_{-h_1}^0
\frac{\cosh{k_{1n}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{1n}h_1}\sinh{k_{2m}h_2}}\,{\rm
d}z\right.\nonumber\\ &\quad\quad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{1n}(z-h_0)}
\cosh{k_{2m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{2m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]
\nonumber\\ & =- T_0 \left[\int_{-h_2}^0
\frac{\cosh{k_{20}}(z+h_2)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{20}h_2}\sinh{k_{2m}h_2}}\,{\rm
d}z\right.\nonumber\\ &\quad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{20}(z-h_0)}
\cosh{k_{2m}(z-h_0)}}{\sinh{k_{20}h_0}\sinh{k_{2m}h_0}}\,{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right]\nonumber\\
&\quad - \sum_{n=1}^\infty T_n \left[\int_{-h_2}^0
\frac{\cosh{k_{2n}}(z+h_2)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{2n}h_2}\sinh{k_{2m}h_2}}\,{\rm
d}z\right.\nonumber\\ &\quad \left.{}+ \int_0^{h_0}
\frac{\cosh{k_{2n}(z-h_0)}
\cosh{k_{2m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{2m}h_0}}{\rm
d}z\vphantom{\int_{-h_1}^0 \frac{\cosh{k_{10}}(z+h_1)
\cosh{k_{2m}(z+h_2)}}{\sinh{k_{10}h_1}\sinh{k_{2m}h_2}}}\right].
\end{align}Then, it is required to calculate the following integrals:
 \begin{equation} \left.\begin{gathered} a^{1)}_{k_{1n}k_{2m}} = \int_0^{h_0} \frac{\cosh{k_{1n}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z,\\ a^{2)}_{k_{2n}k_{2m}} = \int_0^{h_0} \frac{\cosh{k_{2n}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z,\\ a^{3)}_{k_{1n}k_{1m}} = \int_0^{h_0} \frac{\cosh{k_{1n}(z-h_0)} \cosh{k_{1m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{1m}h_0}}\,{\rm d}z,\\ a^{4)}_{k_{2n}k_{1m}} = \int_0^{h_0} \frac{\cosh{k_{2n}(z-h_0)} \cosh{k_{1m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{1m}h_0}}\,{\rm d}z,\\ b^{1)}_{k_{1n} k_{2m}} = \int_{-h_2}^0 \frac{\cosh{k_{1n}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{1n}h_1}\sinh{k_{2m}h_2}}\,{\rm d}z,\\ b^{2)}_{k_{2n} k_{2m}} = \int_{-h_2}^0 \frac{\cosh{k_{2n}}(z+h_2) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{2n}h_2}\sinh{k_{2m}h_2}}\,{\rm d}z,\\ b^{3)}_{k_{1n} k_{1m}} = \int_{-h_1}^0 \frac{\cosh{k_{1n}}(z+h_1) \cosh{k_{1m}(z+h_1)}}{\sinh{k_{1n}h_1}\sinh{k_{1m}h_1}}\,{\rm d}z,\\ b^{4)}_{k_{2n} k_{1m}} = \int_{-h_1}^0 \frac{\cosh{k_{2n}}(z+h_2) \cosh{k_{1m}(z+h_1)}}{\sinh{k_{2n}h_2}\sinh{k_{1m}h_1}}\,{\rm d}z. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} a^{1)}_{k_{1n}k_{2m}} = \int_0^{h_0} \frac{\cosh{k_{1n}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z,\\ a^{2)}_{k_{2n}k_{2m}} = \int_0^{h_0} \frac{\cosh{k_{2n}(z-h_0)} \cosh{k_{2m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{2m}h_0}}\,{\rm d}z,\\ a^{3)}_{k_{1n}k_{1m}} = \int_0^{h_0} \frac{\cosh{k_{1n}(z-h_0)} \cosh{k_{1m}(z-h_0)}}{\sinh{k_{1n}h_0}\sinh{k_{1m}h_0}}\,{\rm d}z,\\ a^{4)}_{k_{2n}k_{1m}} = \int_0^{h_0} \frac{\cosh{k_{2n}(z-h_0)} \cosh{k_{1m}(z-h_0)}}{\sinh{k_{2n}h_0}\sinh{k_{1m}h_0}}\,{\rm d}z,\\ b^{1)}_{k_{1n} k_{2m}} = \int_{-h_2}^0 \frac{\cosh{k_{1n}}(z+h_1) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{1n}h_1}\sinh{k_{2m}h_2}}\,{\rm d}z,\\ b^{2)}_{k_{2n} k_{2m}} = \int_{-h_2}^0 \frac{\cosh{k_{2n}}(z+h_2) \cosh{k_{2m}(z+h_2)}}{\sinh{k_{2n}h_2}\sinh{k_{2m}h_2}}\,{\rm d}z,\\ b^{3)}_{k_{1n} k_{1m}} = \int_{-h_1}^0 \frac{\cosh{k_{1n}}(z+h_1) \cosh{k_{1m}(z+h_1)}}{\sinh{k_{1n}h_1}\sinh{k_{1m}h_1}}\,{\rm d}z,\\ b^{4)}_{k_{2n} k_{1m}} = \int_{-h_1}^0 \frac{\cosh{k_{2n}}(z+h_2) \cosh{k_{1m}(z+h_1)}}{\sinh{k_{2n}h_2}\sinh{k_{1m}h_1}}\,{\rm d}z. \end{gathered}\right\} \end{equation}In short, we need to calculate three types of integrals:
Here, ![]() $h$ is an arbitrary constant, which may be either
$h$ is an arbitrary constant, which may be either ![]() $h_0$, or
$h_0$, or ![]() $h_1$ or
$h_1$ or ![]() $h_2$. Note that
$h_2$. Note that ![]() $d$ is also an arbitrary constant such that
$d$ is also an arbitrary constant such that ![]() $d \ne h$. For example, if
$d \ne h$. For example, if ![]() $h = h_1$, then
$h = h_1$, then ![]() $d = h_2$, and vice versa. Consequently, (A3) and (A4) in the case
$d = h_2$, and vice versa. Consequently, (A3) and (A4) in the case ![]() $h_1\geq h_2$ reduce to the form
$h_1\geq h_2$ reduce to the form
 \begin{align} \begin{cases} \displaystyle \frac{\mathrm{i}R_0}{k_{10}} \left[b^{1)}_{k_{10}k_{2m}} + a^{1)}_{k_{10}k_{2m}}\right] + \displaystyle \sum_{n=1}^\infty \frac{R_n}{k_{1n}} \left[b^{1)}_{k_{1n}k_{2m}} + a^{1)}_{k_{1n}k_{2m}}\right] - \frac{\mathrm{i}T_0}{k_{20}} \left[b^{2)}_{k_{20}k_{2m}} + a^{2)}_{k_{20}k_{2m}}\right] \\ \quad\quad - \displaystyle \sum_{n=1}^\infty \frac{T_n}{k_{2n}} \left[b^{2)}_{k_{2n}k_{2m}} + a^{2)}_{k_{2n}k_{2m}}\right] =-\frac{\mathrm{i}}{k_{10}} \left[b^{1)}_{k_{10}k_{2m}} + a^{1)}_{k_{10}k_{2m}}\right],\\ - R_0 \left[b^{3)}_{k_{10}k_{1m}} + a^{3)}_{k_{10}k_{1m}}\right] - \displaystyle \sum_{n=1}^\infty R_n \left[b^{3)}_{k_{1n}k_{1m}} + a^{3)}_{k_{1n}k_{1m}}\right] \\ \quad\quad {}- T_0 \left[b^{4)}_{k_{20}k_{1m}}\,H(z+h_2) + a^{4)}_{k_{20}k_{1m}}\right] - \displaystyle \sum_{n=1}^\infty T_n \left[b^{4)}_{k_{2n}k_{1m}}\,H(z+h_2) + a^{4)}_{k_{2n}k_{1m}}\right]\\ \quad =- \left[b^{3)}_{k_{10}k_{1m}} + a^{3)}_{k_{10}k_{1m}}\right]. \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle \frac{\mathrm{i}R_0}{k_{10}} \left[b^{1)}_{k_{10}k_{2m}} + a^{1)}_{k_{10}k_{2m}}\right] + \displaystyle \sum_{n=1}^\infty \frac{R_n}{k_{1n}} \left[b^{1)}_{k_{1n}k_{2m}} + a^{1)}_{k_{1n}k_{2m}}\right] - \frac{\mathrm{i}T_0}{k_{20}} \left[b^{2)}_{k_{20}k_{2m}} + a^{2)}_{k_{20}k_{2m}}\right] \\ \quad\quad - \displaystyle \sum_{n=1}^\infty \frac{T_n}{k_{2n}} \left[b^{2)}_{k_{2n}k_{2m}} + a^{2)}_{k_{2n}k_{2m}}\right] =-\frac{\mathrm{i}}{k_{10}} \left[b^{1)}_{k_{10}k_{2m}} + a^{1)}_{k_{10}k_{2m}}\right],\\ - R_0 \left[b^{3)}_{k_{10}k_{1m}} + a^{3)}_{k_{10}k_{1m}}\right] - \displaystyle \sum_{n=1}^\infty R_n \left[b^{3)}_{k_{1n}k_{1m}} + a^{3)}_{k_{1n}k_{1m}}\right] \\ \quad\quad {}- T_0 \left[b^{4)}_{k_{20}k_{1m}}\,H(z+h_2) + a^{4)}_{k_{20}k_{1m}}\right] - \displaystyle \sum_{n=1}^\infty T_n \left[b^{4)}_{k_{2n}k_{1m}}\,H(z+h_2) + a^{4)}_{k_{2n}k_{1m}}\right]\\ \quad =- \left[b^{3)}_{k_{10}k_{1m}} + a^{3)}_{k_{10}k_{1m}}\right]. \end{cases} \end{align}
Proceeding similarly, (A5) and (A6) for ![]() $h_1 \leq h_2$ reduce to
$h_1 \leq h_2$ reduce to
 \begin{align} \begin{cases} \displaystyle \frac{\mathrm{i}R_0}{k_{10}} \left[b^{3)}_{k_{10}k_{1m}} + a^{3)}_{k_{10}k_{1m}}\right] + \displaystyle \sum_{n=1}^\infty \frac{R_n}{k_{1n}} \left[b^{3)}_{k_{1n}k_{1m}} + a^{3)}_{k_{1n}k_{1m}}\right] - \frac{\mathrm{i}T_0}{k_{20}} \left[b^{4)}_{k_{20}k_{1m}} + a^{4)}_{k_{20}k_{1m}}\right] \\ \quad\quad- \displaystyle \sum_{n=1}^\infty \frac{T_n}{k_{2n}} \left[b^{4)}_{k_{2n}k_{1m}} + a^{4)}_{k_{2n}k_{1m}}\right] =- \frac{\mathrm{i}}{k_{10}} \left[b^{3)}_{k_{10}k_{1m}} + a^{3)}_{k_{10}k_{1m}}\right],\\ - R_0 \left[b^{1)}_{k_{10}k_{2m}}\,H(z+h_1) + a^{1)}_{k_{10}k_{2m}}\right] - \displaystyle \sum_{n=1}^\infty R_n \left[b^{1)}_{k_{1n}k_{2m}}\,H(z+h_1) + a^{1)}_{k_{1n}k_{2m}}\right]\\ \quad\quad {}- T_0 \left[b^{2)}_{k_{20}k_{2m}} + a^{2)}_{k_{20}k_{2m}}\right] - \displaystyle \sum_{n=1}^\infty T_n \left[b^{2)}_{k_{2n}k_{2m}} + a^{2)}_{k_{2n}k_{2m}}\right] \\ \quad =- \left[b^{1)}_{k_{10}k_{2m}}\,H(z+h_1) + a^{1)}_{k_{10}k_{2m}}\right]. \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle \frac{\mathrm{i}R_0}{k_{10}} \left[b^{3)}_{k_{10}k_{1m}} + a^{3)}_{k_{10}k_{1m}}\right] + \displaystyle \sum_{n=1}^\infty \frac{R_n}{k_{1n}} \left[b^{3)}_{k_{1n}k_{1m}} + a^{3)}_{k_{1n}k_{1m}}\right] - \frac{\mathrm{i}T_0}{k_{20}} \left[b^{4)}_{k_{20}k_{1m}} + a^{4)}_{k_{20}k_{1m}}\right] \\ \quad\quad- \displaystyle \sum_{n=1}^\infty \frac{T_n}{k_{2n}} \left[b^{4)}_{k_{2n}k_{1m}} + a^{4)}_{k_{2n}k_{1m}}\right] =- \frac{\mathrm{i}}{k_{10}} \left[b^{3)}_{k_{10}k_{1m}} + a^{3)}_{k_{10}k_{1m}}\right],\\ - R_0 \left[b^{1)}_{k_{10}k_{2m}}\,H(z+h_1) + a^{1)}_{k_{10}k_{2m}}\right] - \displaystyle \sum_{n=1}^\infty R_n \left[b^{1)}_{k_{1n}k_{2m}}\,H(z+h_1) + a^{1)}_{k_{1n}k_{2m}}\right]\\ \quad\quad {}- T_0 \left[b^{2)}_{k_{20}k_{2m}} + a^{2)}_{k_{20}k_{2m}}\right] - \displaystyle \sum_{n=1}^\infty T_n \left[b^{2)}_{k_{2n}k_{2m}} + a^{2)}_{k_{2n}k_{2m}}\right] \\ \quad =- \left[b^{1)}_{k_{10}k_{2m}}\,H(z+h_1) + a^{1)}_{k_{10}k_{2m}}\right]. \end{cases} \end{align}
Here, the integrals ![]() $a^{1)-4)}_{\alpha _n \beta _m}, b^{1),4)}_{\alpha _n \beta _m}$ and
$a^{1)-4)}_{\alpha _n \beta _m}, b^{1),4)}_{\alpha _n \beta _m}$ and ![]() $b^{2),3)}_{\beta _n \beta _m}$ are evaluated as
$b^{2),3)}_{\beta _n \beta _m}$ are evaluated as
 \begin{align} a^{1)-4)}_{\alpha_n \beta_m} &= \int_0^h \frac{\cosh{\alpha_n (z-h)} \cosh{\beta_m (z-h)}}{\sinh{\alpha_n h} \sinh{\beta_m h}}\,{\rm d}z\nonumber\\ &=\begin{cases} \displaystyle \frac{\alpha_n \coth{\beta_m h} - \beta_m \coth{\alpha_n h}}{\alpha_n^2 - \beta_m ^2} & \mbox{for } \alpha_n \ne \beta_m, \\[10pt] \displaystyle \frac{{\rm e}^{4\alpha_n h} + 4 \alpha_n h\,{\rm e}^{2 \alpha_n h} - 1}{2 \alpha_n (1 - {\rm e}^{2 \alpha_n h})^2} & \mbox{for } \alpha_n = \beta_m, \end{cases} \end{align}
\begin{align} a^{1)-4)}_{\alpha_n \beta_m} &= \int_0^h \frac{\cosh{\alpha_n (z-h)} \cosh{\beta_m (z-h)}}{\sinh{\alpha_n h} \sinh{\beta_m h}}\,{\rm d}z\nonumber\\ &=\begin{cases} \displaystyle \frac{\alpha_n \coth{\beta_m h} - \beta_m \coth{\alpha_n h}}{\alpha_n^2 - \beta_m ^2} & \mbox{for } \alpha_n \ne \beta_m, \\[10pt] \displaystyle \frac{{\rm e}^{4\alpha_n h} + 4 \alpha_n h\,{\rm e}^{2 \alpha_n h} - 1}{2 \alpha_n (1 - {\rm e}^{2 \alpha_n h})^2} & \mbox{for } \alpha_n = \beta_m, \end{cases} \end{align} \begin{align} b^{1),4)}_{\alpha_n \beta_m} & = \int_{-h}^0 \frac{\cosh{\alpha_n (z+d)} \cosh{\beta_m (z+h)}}{\sinh{\alpha_n d} \sinh{\beta_m h}}\,{\rm d}z,\nonumber\\ & = \begin{cases} \displaystyle \frac{\begin{array}{@{}c@{}}\alpha_n \{\sinh{\alpha_n(h-d)} + \cosh{\beta_m h} \sinh{\alpha_n d}\}\\ +\, \beta_m \sinh{\beta_m h} \cosh{\alpha_n d} \end{array}}{\sinh{\beta_m h} \sinh{\alpha_n d}\,(\alpha_n^2 - \beta_m^2)} & \mbox{for } \alpha_n \ne \beta_m,\\[10pt] \displaystyle \frac{\coth{\alpha_n d} \{1 + h \alpha_n \coth{\alpha_n h}\} - \alpha_n h}{2 \alpha_n } & \mbox{for } \alpha_n = \beta_m, \end{cases} \end{align}
\begin{align} b^{1),4)}_{\alpha_n \beta_m} & = \int_{-h}^0 \frac{\cosh{\alpha_n (z+d)} \cosh{\beta_m (z+h)}}{\sinh{\alpha_n d} \sinh{\beta_m h}}\,{\rm d}z,\nonumber\\ & = \begin{cases} \displaystyle \frac{\begin{array}{@{}c@{}}\alpha_n \{\sinh{\alpha_n(h-d)} + \cosh{\beta_m h} \sinh{\alpha_n d}\}\\ +\, \beta_m \sinh{\beta_m h} \cosh{\alpha_n d} \end{array}}{\sinh{\beta_m h} \sinh{\alpha_n d}\,(\alpha_n^2 - \beta_m^2)} & \mbox{for } \alpha_n \ne \beta_m,\\[10pt] \displaystyle \frac{\coth{\alpha_n d} \{1 + h \alpha_n \coth{\alpha_n h}\} - \alpha_n h}{2 \alpha_n } & \mbox{for } \alpha_n = \beta_m, \end{cases} \end{align} \begin{align} b^{2),3)}_{\beta_n \beta_m} & = \int_{-h}^0 \frac{\cosh{\beta_n (z+h)} \cosh{\beta_m (z+h)}}{\sinh{\beta_n h} \sinh{\beta_m h}}\,{\rm d}z, \nonumber\\ &=\begin{cases} \displaystyle \frac{\beta_n \coth{\beta_m h} - \beta_m \coth{\beta_n h}}{(\beta_n^2 - \beta_m^2)} & \mbox{for } \beta_m \ne \beta_n,\\[10pt] \displaystyle \frac{{\rm e}^{4 \beta_n h} + 4 \beta_n h\,{\rm e}^{2 \beta_n h} - 1}{2 \beta_n (1 - {\rm e}^{2 \beta_n h})^2} & \mbox{for } \beta_n = \beta_m. \end{cases} \end{align}
\begin{align} b^{2),3)}_{\beta_n \beta_m} & = \int_{-h}^0 \frac{\cosh{\beta_n (z+h)} \cosh{\beta_m (z+h)}}{\sinh{\beta_n h} \sinh{\beta_m h}}\,{\rm d}z, \nonumber\\ &=\begin{cases} \displaystyle \frac{\beta_n \coth{\beta_m h} - \beta_m \coth{\beta_n h}}{(\beta_n^2 - \beta_m^2)} & \mbox{for } \beta_m \ne \beta_n,\\[10pt] \displaystyle \frac{{\rm e}^{4 \beta_n h} + 4 \beta_n h\,{\rm e}^{2 \beta_n h} - 1}{2 \beta_n (1 - {\rm e}^{2 \beta_n h})^2} & \mbox{for } \beta_n = \beta_m. \end{cases} \end{align}
It is important to emphasize that when dealing with gravitational waves at the interface between two layers of arbitrary density, the eigenfunctions ![]() $f_{jm}$,
$f_{jm}$, ![]() $j=1,2$, associated with the set of propagating and evanescent wave modes defined by the dispersion relation (3.2) are generally non-orthogonal. However, if we restrict our analysis to fluids with almost the same densities (in the Boussinesq approximation; Brekhovskikh & Goncharov Reference Brekhovskikh and Goncharov1994), then the eigenfunctions become orthogonal, and the corresponding dispersion relation (3.2) reduces to
$j=1,2$, associated with the set of propagating and evanescent wave modes defined by the dispersion relation (3.2) are generally non-orthogonal. However, if we restrict our analysis to fluids with almost the same densities (in the Boussinesq approximation; Brekhovskikh & Goncharov Reference Brekhovskikh and Goncharov1994), then the eigenfunctions become orthogonal, and the corresponding dispersion relation (3.2) reduces to
where ![]() $g' = (1-a) g$ is the reduced acceleration due to gravity. In this case, the following relationship holds:
$g' = (1-a) g$ is the reduced acceleration due to gravity. In this case, the following relationship holds:
 \begin{align} & \alpha_n \coth{\beta_m h_0} - \beta_m \coth{\alpha_n h_0} + \alpha_n \coth{\beta_m h_1} - \beta_m \coth{\alpha_n h_1}\nonumber\\ &\quad = \alpha_n (\coth{\beta_m h_0} + \coth{\beta_m h_1}) - \beta_m (\coth{\alpha_n h_0} + \coth{\alpha_n h_1})\nonumber\\ &\quad = \alpha_n \beta_m g'/\omega^2 - \beta_m \alpha_n g'/\omega^2 = 0. \end{align}
\begin{align} & \alpha_n \coth{\beta_m h_0} - \beta_m \coth{\alpha_n h_0} + \alpha_n \coth{\beta_m h_1} - \beta_m \coth{\alpha_n h_1}\nonumber\\ &\quad = \alpha_n (\coth{\beta_m h_0} + \coth{\beta_m h_1}) - \beta_m (\coth{\alpha_n h_0} + \coth{\alpha_n h_1})\nonumber\\ &\quad = \alpha_n \beta_m g'/\omega^2 - \beta_m \alpha_n g'/\omega^2 = 0. \end{align}
This leads to the identity ![]() $a^{1)-4)}_{\beta _n \beta _m}+b^{2),3)}_{\beta _n \beta _m} = 0$ for
$a^{1)-4)}_{\beta _n \beta _m}+b^{2),3)}_{\beta _n \beta _m} = 0$ for ![]() $n \ne m$. However, for the sake of generality, such a simplification will not be used in further calculations.
$n \ne m$. However, for the sake of generality, such a simplification will not be used in further calculations.
Next, we evaluate integrals in (A11):
 \begin{align} & a^{1)}_{k_{1n}k_{2m}} +
b^{1)}_{k_{1n} k_{2m}} \nonumber\\ &\quad = \begin{cases}
\displaystyle \frac{\begin{array}{@{}c@{}}k_{1n} \{\sinh{k_{1n}(h_1 - h_2)} -
\cosh{k_{2m} h_2} \sinh{k_{1n} h_1}\}\\ +\, k_{2m} \cosh{k_{1n}
h_1} \sinh{k_{2m} h_2}\end{array}}{\sinh{k_{1n} h_1} \sinh{k_{2m} h_2}
(k_{2m}^2 - k_{1n}^2)} & \\[12pt] \displaystyle \quad {}-
\frac{k_{1n}\coth{k_{2m} h_0}}{
k_{2m}^2 - k_{1n}^2} + \frac{k_{1n} k_{2m} \cosh{k_{2m} h_0}
\coth{k_{1n} h_0}}{ k_{2m}^2 - k_{1n}^2} & \mbox{for }
k_{1n} \ne k_{2m},\\[12pt] \displaystyle \frac{{\rm e}^{4 k_{1n}
h_0} + 4 k_{1n} h_0\,{\rm e}^{2 k_{1n} h_0} - 1}{2 k_{1n}
(1 - {\rm e}^{2 k_{1n} h_0})^2} & \\[12pt] \displaystyle
\quad {}+ \frac{\coth{k_{1n} h_1}\,\{1 + k_{1n} h_2
\coth{k_{1n} h_2}\} - k_{1n} h_2}{2 k_{1n} } & \mbox{for
} k_{1n} = k_{2m}, \end{cases}
\end{align}
\begin{align} & a^{1)}_{k_{1n}k_{2m}} +
b^{1)}_{k_{1n} k_{2m}} \nonumber\\ &\quad = \begin{cases}
\displaystyle \frac{\begin{array}{@{}c@{}}k_{1n} \{\sinh{k_{1n}(h_1 - h_2)} -
\cosh{k_{2m} h_2} \sinh{k_{1n} h_1}\}\\ +\, k_{2m} \cosh{k_{1n}
h_1} \sinh{k_{2m} h_2}\end{array}}{\sinh{k_{1n} h_1} \sinh{k_{2m} h_2}
(k_{2m}^2 - k_{1n}^2)} & \\[12pt] \displaystyle \quad {}-
\frac{k_{1n}\coth{k_{2m} h_0}}{
k_{2m}^2 - k_{1n}^2} + \frac{k_{1n} k_{2m} \cosh{k_{2m} h_0}
\coth{k_{1n} h_0}}{ k_{2m}^2 - k_{1n}^2} & \mbox{for }
k_{1n} \ne k_{2m},\\[12pt] \displaystyle \frac{{\rm e}^{4 k_{1n}
h_0} + 4 k_{1n} h_0\,{\rm e}^{2 k_{1n} h_0} - 1}{2 k_{1n}
(1 - {\rm e}^{2 k_{1n} h_0})^2} & \\[12pt] \displaystyle
\quad {}+ \frac{\coth{k_{1n} h_1}\,\{1 + k_{1n} h_2
\coth{k_{1n} h_2}\} - k_{1n} h_2}{2 k_{1n} } & \mbox{for
} k_{1n} = k_{2m}, \end{cases}
\end{align} \begin{align} &a^{2)}_{k_{2n}k_{2m}} + b^{2)}_{k_{2n} k_{2m}}\nonumber\\ &\quad =\begin{cases} \displaystyle \frac{k_{2m} \coth{k_{2n} h_0}}{ k_{2m}^2 - k_{1n}^2} - \frac{k_{2n} \coth{k_{2m} h_2}}{k_{2m}^2 - k_{2n}^2} - \displaystyle\frac{k_{2n} \coth{k_{2m} h_0}}{ k_{2m}^2 - k_{1n}^2} + \frac{k_{2m} \coth{k_{2n} h_2}}{ k_{2m}^2 - k_{2n}^2} & \mbox{for } m\ne n,\\[12pt] \dfrac{{\rm e}^{4 h_0 k_{2m}} + 4 k_{2m} h_0\,{\rm e}^{2 k_{2m} h_0} - 1}{2 k_{2m} ({\rm e}^{2 k_{2m} h_0} - 1)^2} + \dfrac{{\rm e}^{4 h_2 k_{2m}} + 4 k_{2m} h_2\,{\rm e}^{2 h_2 k_{2m}} - 1}{2 k_{2m} ({\rm e}^{2 k_{2m} h_2} - 1)^2} & \mbox{for } m=n, \end{cases} \end{align}
\begin{align} &a^{2)}_{k_{2n}k_{2m}} + b^{2)}_{k_{2n} k_{2m}}\nonumber\\ &\quad =\begin{cases} \displaystyle \frac{k_{2m} \coth{k_{2n} h_0}}{ k_{2m}^2 - k_{1n}^2} - \frac{k_{2n} \coth{k_{2m} h_2}}{k_{2m}^2 - k_{2n}^2} - \displaystyle\frac{k_{2n} \coth{k_{2m} h_0}}{ k_{2m}^2 - k_{1n}^2} + \frac{k_{2m} \coth{k_{2n} h_2}}{ k_{2m}^2 - k_{2n}^2} & \mbox{for } m\ne n,\\[12pt] \dfrac{{\rm e}^{4 h_0 k_{2m}} + 4 k_{2m} h_0\,{\rm e}^{2 k_{2m} h_0} - 1}{2 k_{2m} ({\rm e}^{2 k_{2m} h_0} - 1)^2} + \dfrac{{\rm e}^{4 h_2 k_{2m}} + 4 k_{2m} h_2\,{\rm e}^{2 h_2 k_{2m}} - 1}{2 k_{2m} ({\rm e}^{2 k_{2m} h_2} - 1)^2} & \mbox{for } m=n, \end{cases} \end{align} \begin{align} &a^{3)}_{k_{1n}k_{1m}} + b^{3)}_{k_{1n}k_{1m}}\nonumber\\ &\quad = \begin{cases} \displaystyle \frac{k_{1m} (\coth{k_{1n} h_0} - \coth{k_{1n}h_1}) - k_{1n} (\coth{k_{1m} h_1} + \coth{k_{1m} h_0})}{ k_{1m}^2 - k_{1n}^2} & \mbox{for } m\ne n,\\[12pt] \displaystyle \frac{{\rm e}^{4 k_{1n} h_0} + 4 k_{1n} h_0\,{\rm e}^{2 k_{1n} h_0} - 1}{2 k_{1n} ({\rm e}^{2 k_{1n} h_0} - 1)^2} + \frac{{\rm e}^{4 k_{1n} h_1} + 4 k_{1n} h_1\,{\rm e}^{2 k_{1n} h_1} - 1}{2 k_{1n} ({\rm e}^{2 k_{1n} h_1} - 1)^2} & \mbox{for } m=n, \end{cases} \end{align}
\begin{align} &a^{3)}_{k_{1n}k_{1m}} + b^{3)}_{k_{1n}k_{1m}}\nonumber\\ &\quad = \begin{cases} \displaystyle \frac{k_{1m} (\coth{k_{1n} h_0} - \coth{k_{1n}h_1}) - k_{1n} (\coth{k_{1m} h_1} + \coth{k_{1m} h_0})}{ k_{1m}^2 - k_{1n}^2} & \mbox{for } m\ne n,\\[12pt] \displaystyle \frac{{\rm e}^{4 k_{1n} h_0} + 4 k_{1n} h_0\,{\rm e}^{2 k_{1n} h_0} - 1}{2 k_{1n} ({\rm e}^{2 k_{1n} h_0} - 1)^2} + \frac{{\rm e}^{4 k_{1n} h_1} + 4 k_{1n} h_1\,{\rm e}^{2 k_{1n} h_1} - 1}{2 k_{1n} ({\rm e}^{2 k_{1n} h_1} - 1)^2} & \mbox{for } m=n, \end{cases} \end{align} \begin{align} &a^{4)}_{k_{2n}k_{1m}}\,H(z+h_2) + b^{4)}_{k_{2n}k_{1m}} \nonumber\\ &\quad= \begin{cases} \displaystyle - \frac{k_{1m} \{\sinh{k_{1m} (h_1 - h_2)} - \cosh{k_{2n} h_2} \sinh{k_{1m} h_1}\} + k_{2n} \cosh{k_{1m} h_1} \sinh{k_{2n} h_2}}{\sinh{k_{1m} h_1} \sinh{k_{2n} h_2}\,(k_{1m}^2 - k_{2n}^2)}\\[12pt] \displaystyle \quad{}+\frac{k_{1m} \coth{k_{2n} h_0} - k_{2n} \coth{k_{1m} h_0}}{ k_{1m}^2 - k_{2n}^2} \qquad\qquad\quad \mbox{for } k_{1m}\ne k_{2n},\\[12pt] \displaystyle \frac{{\rm e}^{4 k_{2n} h_0} + 4 k_{2n} h_0\,{\rm e}^{2 k_{2n} h_0} - 1}{2 k_{2n} (1 - {\rm e}^{2 k_{2n} h_0})^2} - \frac{h_2}{2} \\[12pt]\displaystyle \quad{}+ \frac{\cosh{k_{2n} h_1}\,\{\sinh{k_{2n} h_2} + k_{2n} h_2 \cosh{k_{2n} h_2}\}}{2 k_{2n} \sinh{k_{2n} h_1} \sinh{k_{2n} h_2}} \quad \mbox{for } k_{1n} = k_{2m}. \end{cases} \end{align}
\begin{align} &a^{4)}_{k_{2n}k_{1m}}\,H(z+h_2) + b^{4)}_{k_{2n}k_{1m}} \nonumber\\ &\quad= \begin{cases} \displaystyle - \frac{k_{1m} \{\sinh{k_{1m} (h_1 - h_2)} - \cosh{k_{2n} h_2} \sinh{k_{1m} h_1}\} + k_{2n} \cosh{k_{1m} h_1} \sinh{k_{2n} h_2}}{\sinh{k_{1m} h_1} \sinh{k_{2n} h_2}\,(k_{1m}^2 - k_{2n}^2)}\\[12pt] \displaystyle \quad{}+\frac{k_{1m} \coth{k_{2n} h_0} - k_{2n} \coth{k_{1m} h_0}}{ k_{1m}^2 - k_{2n}^2} \qquad\qquad\quad \mbox{for } k_{1m}\ne k_{2n},\\[12pt] \displaystyle \frac{{\rm e}^{4 k_{2n} h_0} + 4 k_{2n} h_0\,{\rm e}^{2 k_{2n} h_0} - 1}{2 k_{2n} (1 - {\rm e}^{2 k_{2n} h_0})^2} - \frac{h_2}{2} \\[12pt]\displaystyle \quad{}+ \frac{\cosh{k_{2n} h_1}\,\{\sinh{k_{2n} h_2} + k_{2n} h_2 \cosh{k_{2n} h_2}\}}{2 k_{2n} \sinh{k_{2n} h_1} \sinh{k_{2n} h_2}} \quad \mbox{for } k_{1n} = k_{2m}. \end{cases} \end{align}Subsequently, by solving a finite system of linear equations as in each of (A11) and (A12) for a finite number of sum terms, say ![]() $N$, the unknowns
$N$, the unknowns ![]() $R_n$ and
$R_n$ and ![]() $T_n$ can be determined. It is pertinent to note that the reflection and transmission coefficients
$T_n$ can be determined. It is pertinent to note that the reflection and transmission coefficients ![]() $K_r$ and
$K_r$ and ![]() $K_t$ are defined as
$K_t$ are defined as ![]() $K_r = |R_n|$ and
$K_r = |R_n|$ and ![]() $K_t = |T_n|$.
$K_t = |T_n|$.
It can be easily verified that the reflection coefficient ![]() $K_r$ and the transmission coefficient
$K_r$ and the transmission coefficient ![]() $K_t$ satisfy the energy balance relation
$K_t$ satisfy the energy balance relation
where ![]() $\chi = c_g(k_t)/c_g(k_{i})$ is the ratio of group speeds of transmitted and incident waves.
$\chi = c_g(k_t)/c_g(k_{i})$ is the ratio of group speeds of transmitted and incident waves.