1. Introduction
Haines jumps occur during the displacement of one fluid by another in porous materials. This process involves rapid redistribution of the liquid, quick movements of the fluid interfaces and fluctuations in pressure (Haines Reference Haines1930). Haines jumps have profound implications for fluid trapping, energy dissipation and saturation hysteresis, relevant to various engineering applications including enhanced oil recovery (Lake et al. Reference Lake, Johns, Rossen and Pope2014), carbon geosequestration (Szulczewski et al. Reference Szulczewski, MacMinn, Herzog and Juanes2012) and underground hydrogen storage (Heinemann et al. Reference Heinemann2021). As a result, the dynamics of Haines jumps has been examined in porous rocks (Berg et al. Reference Berg2013), Hele-Shaw cells (Furuberg, Måløy & Feder Reference Furuberg, Måløy and Feder1996; Armstrong et al. Reference Armstrong, Evseev, Koroteev and Berg2015; Holtzman et al. Reference Holtzman, Dentz, Planet and Ortín2023) and irregular capillaries (Moebius & Or Reference Moebius and Or2012; Jang, Sun & Santamarina Reference Jang, Sun and Santamarina2016). Through microfluidic experiments, Sun & Santamarina (Reference Sun and Santamarina2019) showed that the mechanisms triggering Haines jumps include the deformation of solids, compression of fluids and interactions of multiple menisci. Armstrong et al. (Reference Armstrong, Evseev, Koroteev and Berg2015) investigated the influence zone of Haines jumps under different fluid properties in porous medium micro-models, and revealed the inverse relationship between a Haines jump's time and length scales.
Fundamentally, the dynamics of a Haines jump is a manifestation of the competition between viscous and capillary forces at the pore scale. As a result, apart from being a qualitative indicator of flow regimes of fluid displacement processes, we hypothesise that it can be utilised to quantitatively determine the fluid properties in the multiphase system. Thus, the objectives of this work are to answer the following questions: (i) How can we induce controlled Haines jumps in microfluidic devices, and (ii) how can this be used to infer the fluid properties? Here, we propose a dual-channel structure with a carefully selected geometry. Numerical simulations are conducted for immiscible fluid displacement under various fluid properties in the dual-channel system. Following the characterisation of the fast interface motion during Haines jumps, an analytical model is developed to describe the liquid redistribution process. We show that the fluid viscosity and interfacial tension can be simultaneously determined by analysing the interfacial dynamics during a single Haines jump.
2. Methods
2.1. Geometry of the dual-channel system
The key geometrical feature of our dual-channel geometry is the presence of a width contrast between the two channels and the hierarchies of capillary resistances such that the injected fluid first invades the narrower (top) channel (in the case of the drainage process, corresponding to a contact angle ![]() $\theta >90^\circ$, which is the angle measured within the invading fluid at the triple-contact line) such that the Haines jump can be initialised when gaining access to the bottom channel that has a wider width associated with smaller capillary resistance.
$\theta >90^\circ$, which is the angle measured within the invading fluid at the triple-contact line) such that the Haines jump can be initialised when gaining access to the bottom channel that has a wider width associated with smaller capillary resistance.
Figure 1(a) shows the schematic of the proposed dual-channel system geometry (not to scale). The top channel has a width of ![]() $h_{top}=0.7$ mm, being smaller than the bottom channel width of
$h_{top}=0.7$ mm, being smaller than the bottom channel width of ![]() $h_{bot}=1$ mm. The two channels are separated by a thin wall
$h_{bot}=1$ mm. The two channels are separated by a thin wall ![]() $d=0.1$ mm in width and
$d=0.1$ mm in width and ![]() $W=15$ mm in length. The inlet and outlet channels have the same dimensions of
$W=15$ mm in length. The inlet and outlet channels have the same dimensions of ![]() $l_{in}=l_{out}=1$ mm in length and
$l_{in}=l_{out}=1$ mm in length and ![]() $h_{in}=h_{out}=1$ mm in width. Triangular barriers are placed at the front and rear sides of the bottom and top channels, respectively, reducing the corresponding channel width at respective locations, such that the width at the entrance of the bottom channel is
$h_{in}=h_{out}=1$ mm in width. Triangular barriers are placed at the front and rear sides of the bottom and top channels, respectively, reducing the corresponding channel width at respective locations, such that the width at the entrance of the bottom channel is ![]() $h_{top}=0.7$ mm, and the width at the rear of the top channel is
$h_{top}=0.7$ mm, and the width at the rear of the top channel is ![]() $h_{neck}=0.5$ mm.
$h_{neck}=0.5$ mm.

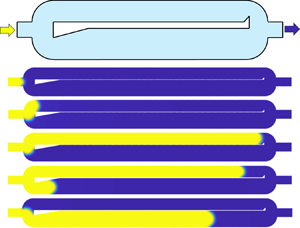
Figure 1. A Haines jump in the dual-channel multiphase system. (a) A schematic showing the geometry and dimensions (not to scale). The uniform channel depth ![]() $D$ (out-of-plane direction) is not shown in the two-dimensional schematic. (b) Snapshots of simulated fluid invasion process in the proposed microfluidic device. The invading fluid is coloured in yellow and the defending fluid is coloured in blue. Images (iii) to (v) correspond to the Haines jump. The inset shows the contact angle
$D$ (out-of-plane direction) is not shown in the two-dimensional schematic. (b) Snapshots of simulated fluid invasion process in the proposed microfluidic device. The invading fluid is coloured in yellow and the defending fluid is coloured in blue. Images (iii) to (v) correspond to the Haines jump. The inset shows the contact angle ![]() $\theta$ which is measured within the invading phase.
$\theta$ which is measured within the invading phase.
We can rationalise the design of the dual-channel system by examining an example of a fluid displacement process from a numerical simulation shown in figure 1(b), with the dynamic viscosities for invading (yellow) and defending (blue) fluids being ![]() $\mu _{inv}=0.001$ Pa
$\mu _{inv}=0.001$ Pa ![]() $\cdot $ s and
$\cdot $ s and ![]() $\mu _{def}=0.003$ Pa
$\mu _{def}=0.003$ Pa ![]() $\cdot $ s, respectively, an interfacial tension of
$\cdot $ s, respectively, an interfacial tension of ![]() $\sigma =0.07$ N m
$\sigma =0.07$ N m![]() $^{-1}$, a contact angle of
$^{-1}$, a contact angle of ![]() $\theta =141^\circ$ (a drainage process) and a constant inlet velocity
$\theta =141^\circ$ (a drainage process) and a constant inlet velocity ![]() $V_{in}=1$ mm s
$V_{in}=1$ mm s![]() $^{-1}$. The viscosity ratio is
$^{-1}$. The viscosity ratio is ![]() $M=\mu _{def}/\mu _{inv}=3$. These fluid properties correspond to case 4 as shown in table 1.
$M=\mu _{def}/\mu _{inv}=3$. These fluid properties correspond to case 4 as shown in table 1.
Table 1. Fluid properties in the simulations.

When the invading fluid reaches the front (left side) of the middle wall (the thin wall separating the two channels), the radii of both the top and bottom arc are both ![]() $h_{top}=0.7$ mm, implying equal capillary resistance. However, as the menisci move forward, the resistance associated with the bottom meniscus becomes greater than the top one due to the sharp-edge-pinning mechanism. This is because the corner angle at the bottom (
$h_{top}=0.7$ mm, implying equal capillary resistance. However, as the menisci move forward, the resistance associated with the bottom meniscus becomes greater than the top one due to the sharp-edge-pinning mechanism. This is because the corner angle at the bottom (![]() $80^\circ$ with
$80^\circ$ with ![]() $\alpha =10^\circ$, defined in figure 1a) is smaller than the top one (
$\alpha =10^\circ$, defined in figure 1a) is smaller than the top one (![]() $90^\circ$) as a result of the triangular protrusion. Therefore, the bottom meniscus is pinned whereas the top meniscus continues to advance (figure 1b-ii,iii). Such a sharp-edge-pinning effect, which is also termed the ‘capillary valve effect’, has been examined thoroughly in the literature and incorporated into numerical algorithms for simulating multiphase flow in porous media with irregular geometries (Wang, Pereira & Gan Reference Wang, Pereira and Gan2021; Wang et al. Reference Wang, Pereira, Sauret, Aryana, Shi and Gan2022).
$90^\circ$) as a result of the triangular protrusion. Therefore, the bottom meniscus is pinned whereas the top meniscus continues to advance (figure 1b-ii,iii). Such a sharp-edge-pinning effect, which is also termed the ‘capillary valve effect’, has been examined thoroughly in the literature and incorporated into numerical algorithms for simulating multiphase flow in porous media with irregular geometries (Wang, Pereira & Gan Reference Wang, Pereira and Gan2021; Wang et al. Reference Wang, Pereira, Sauret, Aryana, Shi and Gan2022).
Once the top meniscus reaches the rear (right) side of the channel, its capillary resistance increases due to the geometrical contraction, resulting in greater capillary resistance compared with the bottom one (since ![]() $h_{neck}< h_{top}$). This leads to the movement of the bottom meniscus, triggering the start of the Haines jump: as the bottom meniscus expands into the bottom channel with
$h_{neck}< h_{top}$). This leads to the movement of the bottom meniscus, triggering the start of the Haines jump: as the bottom meniscus expands into the bottom channel with ![]() $h_{bot}=1$ mm, the smaller capillary resistance within the bottom channel compared with the top one results in the fast retraction of the top meniscus and advancement of the bottom meniscus (figure 1b-iv,v). As we will show later, the liquid redistribution process occurs at a much faster speed than the injection velocity, a typical signature of Haines jumps in the capillary-dominated flow regime during the fluid displacement process.
$h_{bot}=1$ mm, the smaller capillary resistance within the bottom channel compared with the top one results in the fast retraction of the top meniscus and advancement of the bottom meniscus (figure 1b-iv,v). As we will show later, the liquid redistribution process occurs at a much faster speed than the injection velocity, a typical signature of Haines jumps in the capillary-dominated flow regime during the fluid displacement process.
We point out that the expansion angle on the left of the bottom channel ![]() $\alpha$ is set to a relatively small value of
$\alpha$ is set to a relatively small value of ![]() $10^\circ$. This is because a residual defending fluid film can be developed when the geometrical expansion is large (e.g. when
$10^\circ$. This is because a residual defending fluid film can be developed when the geometrical expansion is large (e.g. when ![]() $\alpha =45^\circ$), where the fluid interface becomes unstable and an invading fluid finger grows into the defending fluid, leaving the contact line behind. The critical criterion for the development of the liquid film depends on various factors such as the contact angle and interface velocity, and was examined by Zhao et al. (Reference Zhao, Alizadeh Pahlavan, Cueto-Felgueroso and Juanes2018), who found that a sudden geometrical expansion during the fluid displacement promotes the development of a liquid film. As a result, a small value of
$\alpha =45^\circ$), where the fluid interface becomes unstable and an invading fluid finger grows into the defending fluid, leaving the contact line behind. The critical criterion for the development of the liquid film depends on various factors such as the contact angle and interface velocity, and was examined by Zhao et al. (Reference Zhao, Alizadeh Pahlavan, Cueto-Felgueroso and Juanes2018), who found that a sudden geometrical expansion during the fluid displacement promotes the development of a liquid film. As a result, a small value of ![]() $\alpha =10^\circ$ is chosen in the current work, such that the unstable interface growth is absent.
$\alpha =10^\circ$ is chosen in the current work, such that the unstable interface growth is absent.
2.2. Numerical scheme
The numerical simulations for the two-dimensional (2-D) multiphase flow process in the dual-channel system were performed using the laminar two-phase flow-phase-field model implemented in COMSOL Multiphysics 6.1. The governing equations for fluid motion include the continuity and momentum equations
where ![]() $\rho$ and
$\rho$ and ![]() $\mu$ are the mass density and dynamic viscosity of the fluid,
$\mu$ are the mass density and dynamic viscosity of the fluid, ![]() ${\boldsymbol {U}}$ and
${\boldsymbol {U}}$ and ![]() $P$ are the flow velocity and pressure while
$P$ are the flow velocity and pressure while ![]() ${{\boldsymbol {F}}_{st}}$ is the surface tension force acting at the fluid–fluid interface.
${{\boldsymbol {F}}_{st}}$ is the surface tension force acting at the fluid–fluid interface.
The phase-field method is used for interface tracking and shape modelling, from which the surface tension force ![]() ${{\boldsymbol {F}}_{st}}$ in the momentum equation can be calculated. The order parameter in phase-field models
${{\boldsymbol {F}}_{st}}$ in the momentum equation can be calculated. The order parameter in phase-field models ![]() $\phi$ describes the distribution of different phases in the system. When
$\phi$ describes the distribution of different phases in the system. When ![]() $\phi = 1$, the fluid behaves with the property of the invading phase; when
$\phi = 1$, the fluid behaves with the property of the invading phase; when ![]() $\phi = -1$, the fluid behaves with the property of the defending phase; and
$\phi = -1$, the fluid behaves with the property of the defending phase; and ![]() $\phi = 0$ corresponds to the fluid–fluid interface location. The effective fluid properties including density
$\phi = 0$ corresponds to the fluid–fluid interface location. The effective fluid properties including density ![]() $\rho$ and viscosity
$\rho$ and viscosity ![]() $\mu$ are calculated based on
$\mu$ are calculated based on ![]() $\phi$ using linear interpolation between the two fluids. The governing equation for the phase field is the advective Cahn–Hilliard equation (Cahn & Hilliard Reference Cahn and Hilliard1959)
$\phi$ using linear interpolation between the two fluids. The governing equation for the phase field is the advective Cahn–Hilliard equation (Cahn & Hilliard Reference Cahn and Hilliard1959)
where ![]() $\varepsilon$ is a capillary width representative of the interface thickness,
$\varepsilon$ is a capillary width representative of the interface thickness, ![]() $f$ is the magnitude of the mixing energy, which satisfies
$f$ is the magnitude of the mixing energy, which satisfies ![]() $f=3\epsilon \sigma /\sqrt {8}$ with
$f=3\epsilon \sigma /\sqrt {8}$ with ![]() $\sigma$ the surface tension, and
$\sigma$ the surface tension, and ![]() $\lambda$ is the mobility parameter that controls the rate at which concentration differences are ‘smoothed out’ by diffusion driven by the chemical potential
$\lambda$ is the mobility parameter that controls the rate at which concentration differences are ‘smoothed out’ by diffusion driven by the chemical potential ![]() $\psi$
$\psi$
Subsequently, the surface tension force for the momentum equation is determined by
We refer the readers to Yue et al. (Reference Yue, Feng, Liu and Shen2004) for a detailed description of the phase-field model.
Constant injection velocity and constant pressure boundary conditions are applied at the inlet and outlet, respectively,
The no-slip wall condition is adopted at all solid boundaries.
The computational domain was meshed using triangular elements with a total number of elements of 28 995 and a mesh size ranging from ![]() $7.2 \times 10^{ - 4}$ to 0.05 mm, which are found to be sufficient to give converged results. The maximum element growth rate and curvature factor are set to 1.1 and 0.25, respectively. Simulations were carried out on a Dell workstation (Precision 7920) equipped with an Intel Xeon processor (Gold 6128), and cases in table 1 each take approximately 2 h.
$7.2 \times 10^{ - 4}$ to 0.05 mm, which are found to be sufficient to give converged results. The maximum element growth rate and curvature factor are set to 1.1 and 0.25, respectively. Simulations were carried out on a Dell workstation (Precision 7920) equipped with an Intel Xeon processor (Gold 6128), and cases in table 1 each take approximately 2 h.
3. Results and discussion
3.1. Interface motion during Haines jump in the dual-channel system
To characterise the fluid redistribution process during the Haines jump for the case in figure 1(b), the evolution of the bottom channel meniscus velocity ![]() $u_{bot}$ is plotted in figure 2(a), highlighting four distinct regimes: in regime I the bottom meniscus slowly advances as more invading fluid is injected. In regime II, the bottom meniscus expands into the channel with increasing width (varying from
$u_{bot}$ is plotted in figure 2(a), highlighting four distinct regimes: in regime I the bottom meniscus slowly advances as more invading fluid is injected. In regime II, the bottom meniscus expands into the channel with increasing width (varying from ![]() $h_{top}$ to
$h_{top}$ to ![]() $h_{bot}$ with the inclination angle defined by
$h_{bot}$ with the inclination angle defined by ![]() $\alpha$), which is associated with decreasing capillary resistance. In regime III, both top and bottom menisci move within the respective channels with uniform widths (
$\alpha$), which is associated with decreasing capillary resistance. In regime III, both top and bottom menisci move within the respective channels with uniform widths (![]() $h_{top}$ for the top channel and
$h_{top}$ for the top channel and ![]() $h_{bot}$ for the bottom channel). Finally, the Haines jump finishes when the top meniscus reaches the left-most turn, which is accompanied by an oscillation in the top and bottom menisci due to inertia. The bottom meniscus then advances again at a much lower speed (regime IV). The liquid distributions at these regimes are shown in figure 2(b). See supplementary movie 1 available at https://doi.org/10.1017/jfm.2024.1225 for the Haines jump phenomenon, and movie 2 for the complete process.
$h_{bot}$ for the bottom channel). Finally, the Haines jump finishes when the top meniscus reaches the left-most turn, which is accompanied by an oscillation in the top and bottom menisci due to inertia. The bottom meniscus then advances again at a much lower speed (regime IV). The liquid distributions at these regimes are shown in figure 2(b). See supplementary movie 1 available at https://doi.org/10.1017/jfm.2024.1225 for the Haines jump phenomenon, and movie 2 for the complete process.

Figure 2. Interface dynamics during a Haines jump (case 4). (a) The velocity of the bottom meniscus ![]() $u_{bot}$ as a function of time. (b) Snapshots of liquid distribution at four stages during the Haines jump. The region between the red-dashed lines in (a) and in (b-III) indicates the spatial domain where subsequent analysis is based. Arrows indicate meniscus movement direction. (c) Value of
$u_{bot}$ as a function of time. (b) Snapshots of liquid distribution at four stages during the Haines jump. The region between the red-dashed lines in (a) and in (b-III) indicates the spatial domain where subsequent analysis is based. Arrows indicate meniscus movement direction. (c) Value of ![]() $u_{bot}$ as a function of location
$u_{bot}$ as a function of location ![]() $x_{bot}$. (d) The interface location of the top meniscus
$x_{bot}$. (d) The interface location of the top meniscus ![]() $x_{top}$ inferred from
$x_{top}$ inferred from ![]() $x_{bot}$.
$x_{bot}$.
To gain insights into the fluid property-dependent behaviour of the meniscus velocity during the Haines jump, we focus our attention on regime III, during which both top and bottom menisci move within channels with constant widths. This corresponds to the period in which the location of the bottom meniscus ![]() $x_{bot}$ is between the red-dashed lines in figure 2(a,b). Since
$x_{bot}$ is between the red-dashed lines in figure 2(a,b). Since ![]() $u_{bot}$ is a result of the competition between capillary and viscous forces, and the capillary contrast that drives the motion of fluids remains constant, the decrease in
$u_{bot}$ is a result of the competition between capillary and viscous forces, and the capillary contrast that drives the motion of fluids remains constant, the decrease in ![]() $u_{bot}$ observed in regime III implies that the total viscous dissipation is increasing. Given that the fluid viscosities remain unchanged, the reason for such increased viscous resistance, intuitively, resides in the migration of the more viscous fluid (defending fluid) into the narrower (top) channel, which causes the increase of viscous dissipation for the whole system. We note that the fast fluid redistribution in regime III is effectively a counterclockwise fluid circulation within the channel, as the meniscus travels at a much larger speed (
$u_{bot}$ observed in regime III implies that the total viscous dissipation is increasing. Given that the fluid viscosities remain unchanged, the reason for such increased viscous resistance, intuitively, resides in the migration of the more viscous fluid (defending fluid) into the narrower (top) channel, which causes the increase of viscous dissipation for the whole system. We note that the fast fluid redistribution in regime III is effectively a counterclockwise fluid circulation within the channel, as the meniscus travels at a much larger speed (![]() $\sim$25 mm s
$\sim$25 mm s![]() $^{-1}$) than the injection velocity of 1 mm s
$^{-1}$) than the injection velocity of 1 mm s![]() $^{-1}$. Figure 2(c) shows that, as expected,
$^{-1}$. Figure 2(c) shows that, as expected, ![]() $u_{bot}$ decreases with
$u_{bot}$ decreases with ![]() $x_{bot}$. Although the focus is placed on tracking the bottom meniscus, the top meniscus location
$x_{bot}$. Although the focus is placed on tracking the bottom meniscus, the top meniscus location ![]() $x_{top}$ can be derived from
$x_{top}$ can be derived from ![]() $x_{bot}$ based on the conservation of mass (inset in figure 2c).
$x_{bot}$ based on the conservation of mass (inset in figure 2c).
3.2. Analytical model
The dynamics of the menisci motion during Haines jumps is governed by the balance between the driving capillary force and the dissipating viscous force. The capillary pressure can be described by the Young–Laplace equation ![]() $\Delta P=\sigma (1/r_{in}+1/r_{out})$, where
$\Delta P=\sigma (1/r_{in}+1/r_{out})$, where ![]() $\sigma$,
$\sigma$, ![]() $r_{in}$ and
$r_{in}$ and ![]() $r_{out}$ represent the interfacial tension, in-plane and out-of-plane curvatures, respectively. Therefore, the capillary pressure contrast between the top and bottom channels is
$r_{out}$ represent the interfacial tension, in-plane and out-of-plane curvatures, respectively. Therefore, the capillary pressure contrast between the top and bottom channels is
For a Hele-Shaw cell system with a uniform depth ![]() $D$, (3.1) becomes
$D$, (3.1) becomes
The contact angles at the top and bottom channels can be different due to the contact angle hysteresis (Shi et al. Reference Shi, Zhang, Liu, Hanaor and Gan2018), i.e. the difference between the contact angles during advancing and receding processes as a result of surface imperfections such as roughness and chemical heterogeneity. We note that, due to the channel geometry remaining uniform for each meniscus during Haines jumps (stage III in figure 2b), the capillary contrast ![]() $\Delta P_c$ that drives the fluid circulation can be regarded as constant.
$\Delta P_c$ that drives the fluid circulation can be regarded as constant.
For viscous dissipation, figure 3 shows the schematic of flow segmentation during the Haines jump (fast circulation process). The vertical black-dashed lines divide the flow path into four segments. The total viscous pressure drop of the system during the fluid circulation can be calculated via the summation of individual contributions of different flow segments
For laminar Newtonian flow, one should expect a linear relationship between the flow rate and pressure drop
where ![]() $L$ is the effective segment length. Here,
$L$ is the effective segment length. Here, ![]() $k$ is the permeability of the corresponding segment. Despite commonly being used in porous medium flow, here, the term ‘permeability’ is adopted for channel flows as it captures the geometrical feature while being independent of the fluid property, as opposed to ‘hydraulic conductivity’. The permeability of Newtonian flow in a rectangular channel of width
$k$ is the permeability of the corresponding segment. Despite commonly being used in porous medium flow, here, the term ‘permeability’ is adopted for channel flows as it captures the geometrical feature while being independent of the fluid property, as opposed to ‘hydraulic conductivity’. The permeability of Newtonian flow in a rectangular channel of width ![]() $h$ and depth
$h$ and depth ![]() $D$ is (Boussinesq Reference Boussinesq1868; White Reference White1991)
$D$ is (Boussinesq Reference Boussinesq1868; White Reference White1991)
 \begin{equation} k=\frac{h^2}{12}\left[1-\frac{192h}{{\rm \pi}^5 D} \sum_{n=1}^\infty\frac{1}{(2n-1)^2}\tanh{\frac{(2n-1){\rm \pi} D}{2h}}\right]. \end{equation}
\begin{equation} k=\frac{h^2}{12}\left[1-\frac{192h}{{\rm \pi}^5 D} \sum_{n=1}^\infty\frac{1}{(2n-1)^2}\tanh{\frac{(2n-1){\rm \pi} D}{2h}}\right]. \end{equation}
When the channel depth ![]() $D$ is much greater than the width
$D$ is much greater than the width ![]() $h$, (3.5) is approximated by
$h$, (3.5) is approximated by ![]() $k=h^2/12$. (Note that the viscous pressure drop for non-Newtonian flow is more complex due to the shear-rate-dependent viscosity. We refer readers to Chun et al. (Reference Chun, Boyko, Christov and Feng2024) and Boyko & Stone (Reference Boyko and Stone2021) for recent studies on the pressure drop of a Carreau fluid in rectangular channels.)
$k=h^2/12$. (Note that the viscous pressure drop for non-Newtonian flow is more complex due to the shear-rate-dependent viscosity. We refer readers to Chun et al. (Reference Chun, Boyko, Christov and Feng2024) and Boyko & Stone (Reference Boyko and Stone2021) for recent studies on the pressure drop of a Carreau fluid in rectangular channels.)

Figure 3. A schematic showing the flow segmentation in the dual-channel geometry (not to scale). Vertical black-dashed lines divide the circulated flow path into four segments.
For the considered geometry and flow pathway segmentation shown in figure 3, the channel lengths of each segment are ![]() $L_1=l_{top}+l_{eff,l}$,
$L_1=l_{top}+l_{eff,l}$, ![]() $L_2=W_{top}-l_{top}+l_{eff,r}$,
$L_2=W_{top}-l_{top}+l_{eff,r}$, ![]() $L_3=l_{bot}$ and
$L_3=l_{bot}$ and ![]() $L_4=W_{bot}-l_{bot}$, where
$L_4=W_{bot}-l_{bot}$, where ![]() $l_{eff,l}$ and
$l_{eff,l}$ and ![]() $l_{eff,r}$ are the effective channel lengths on the left (purple-dashed line) and right side (orange-dashed line), respectively. Additionally, with uniform channel depth
$l_{eff,r}$ are the effective channel lengths on the left (purple-dashed line) and right side (orange-dashed line), respectively. Additionally, with uniform channel depth ![]() $D$,
$D$, ![]() $k_1=k_2=k_{top}$ (same channel width
$k_1=k_2=k_{top}$ (same channel width ![]() $h_{top}$) and
$h_{top}$) and ![]() $k_3=k_4=k_{bot}$ (same channel width
$k_3=k_4=k_{bot}$ (same channel width ![]() $h_{top}$). We define the channel width contrast
$h_{top}$). We define the channel width contrast ![]() $h^*=h_{top}/h_{bot}$. The meniscus location in the top channel
$h^*=h_{top}/h_{bot}$. The meniscus location in the top channel ![]() $l_{top}$ can be expressed as a function of the bottom meniscus location
$l_{top}$ can be expressed as a function of the bottom meniscus location ![]() $l_{bot}$ using conservation of mass via
$l_{bot}$ using conservation of mass via ![]() $l_{top}=l_{top,0}+(W_{bot}-l_{bot})/h^*$, with
$l_{top}=l_{top,0}+(W_{bot}-l_{bot})/h^*$, with ![]() $l_{top,0}$ being a reference location (figure 2c). Similarly, the meniscus velocity in the top channel can be expressed as a function of the bottom meniscus velocity and the channel width contrast:
$l_{top,0}$ being a reference location (figure 2c). Similarly, the meniscus velocity in the top channel can be expressed as a function of the bottom meniscus velocity and the channel width contrast: ![]() $u_{top}=u_{bot}/h^*$. Here, we have assumed that the inlet velocity
$u_{top}=u_{bot}/h^*$. Here, we have assumed that the inlet velocity ![]() $u_{in}$ is much smaller than the meniscus velocities during the Haines jumps, i.e. the invading fluid volume injected during the Haines jump is ignored. The error associated with this assumption will be discussed later. With the expressions above and by balancing
$u_{in}$ is much smaller than the meniscus velocities during the Haines jumps, i.e. the invading fluid volume injected during the Haines jump is ignored. The error associated with this assumption will be discussed later. With the expressions above and by balancing ![]() $\Delta P_c=\Delta P_v$, (3.4) can be rearranged into the following form:
$\Delta P_c=\Delta P_v$, (3.4) can be rearranged into the following form:
where
Since in the considered channel geometry ![]() $h_{bot}>h_{top}$,
$h_{bot}>h_{top}$, ![]() $h^*=h_{top}/h_{bot}<1$ and
$h^*=h_{top}/h_{bot}<1$ and ![]() $k_{bot}>k_{top}$, the term within the bracket in (3.7) is positive, which reveals three distinct regimes for the behaviour of the bottom meniscus movement velocity
$k_{bot}>k_{top}$, the term within the bracket in (3.7) is positive, which reveals three distinct regimes for the behaviour of the bottom meniscus movement velocity ![]() $u_{bot}$ as the Haines jump proceeds (increasing
$u_{bot}$ as the Haines jump proceeds (increasing ![]() $l_{bot}$). When the defending fluid is more viscous,
$l_{bot}$). When the defending fluid is more viscous, ![]() $p>0$ and
$p>0$ and ![]() $u_{bot}$ decreases with increasing
$u_{bot}$ decreases with increasing ![]() $l_{bot}$; whereas
$l_{bot}$; whereas ![]() $u_{bot}$ will increase with
$u_{bot}$ will increase with ![]() $l_{bot}$ when the invading fluid is more viscous. When both fluids have the same viscosity,
$l_{bot}$ when the invading fluid is more viscous. When both fluids have the same viscosity, ![]() $p=0$, and the meniscus velocity remains constant.
$p=0$, and the meniscus velocity remains constant.
In the following, we first examine the proposed model with 2-D numerical simulations (![]() $D\gg h$) with varied fluid properties. Then, results when the channel depth is comparable to the width are discussed.
$D\gg h$) with varied fluid properties. Then, results when the channel depth is comparable to the width are discussed.
3.3. Numerical simulation
Our 2-D numerical simulation of Newtonian fluids corresponds to the cases where the channel depth is much greater than the channel width, and the channel width dominates the viscous dissipation. The fluid properties, including the viscosities of invading and defending fluids, interfacial tension and contact angle are varied, and are summarised in table 1. A constant inlet velocity ![]() $V_{in}=1$ mm s
$V_{in}=1$ mm s![]() $^{-1}$ is imposed for all simulations.
$^{-1}$ is imposed for all simulations.
Figure 4(a) plots the velocity of the bottom meniscus ![]() $u_{bot}$ as a function of its location
$u_{bot}$ as a function of its location ![]() $l_{bot}$ during Haines jumps. It can be seen that
$l_{bot}$ during Haines jumps. It can be seen that ![]() $u_{bot}$ can either increase, decrease or remain constant depending on the relative magnitude of
$u_{bot}$ can either increase, decrease or remain constant depending on the relative magnitude of ![]() $\mu _{inv}$ to
$\mu _{inv}$ to ![]() $\mu _{def}$, consistent with the theory.
$\mu _{def}$, consistent with the theory.

Figure 4. Model validation of the interface dynamics during a Haines jump. (a) Bottom interface velocity ![]() $u_{bot}$ as a function of location
$u_{bot}$ as a function of location ![]() $l_{bot}$. Refer to table 1 for fluid properties. (b) The relative error in the bottom meniscus location estimation as a function of average bottom meniscus velocity during Haines jumps. (c) A linear relation between the viscosity ratio
$l_{bot}$. Refer to table 1 for fluid properties. (b) The relative error in the bottom meniscus location estimation as a function of average bottom meniscus velocity during Haines jumps. (c) A linear relation between the viscosity ratio ![]() $M$ and the term
$M$ and the term ![]() $l_{eff,l}+Ml_{eff,r}$ demonstrates the fluid property independence of the fitting parameters
$l_{eff,l}+Ml_{eff,r}$ demonstrates the fluid property independence of the fitting parameters ![]() $l_{eff,l}$ and
$l_{eff,l}$ and ![]() $l_{eff,r}$. (d) Comparison between
$l_{eff,r}$. (d) Comparison between ![]() $u_{bot}$ from simulation and calculated from (3.9). Note that the overlaps of yellow markers are due to the constant velocity under
$u_{bot}$ from simulation and calculated from (3.9). Note that the overlaps of yellow markers are due to the constant velocity under ![]() $M=1$ (horizontal lines in (a)).
$M=1$ (horizontal lines in (a)).
By defining the viscosity ratio ![]() $M=\mu _{def}/\mu _{inv}$, and using
$M=\mu _{def}/\mu _{inv}$, and using ![]() $k=h^2/12$ for the permeability, one obtains the governing equation that captures the competition between viscous and capillary forces during the Haines jump in the dual-channel system
$k=h^2/12$ for the permeability, one obtains the governing equation that captures the competition between viscous and capillary forces during the Haines jump in the dual-channel system
 \begin{align} &(1-M)\left(l_{top,0}+\frac{W_{bot}}{h^*}\right)+M(W_{top}+h^{*3}W_{bot})+l_{eff,l}+Ml_{eff,r}\nonumber\\ &\quad+(h^{*3}-1)(1-M)l_{bot}=\frac{\sigma(\cos{\theta_{top}}-h^*\cos{\theta_{bot}})h^*h_{top}}{6\mu_{inv}} \boldsymbol{\cdot}\frac{1}{u_{bot}}. \end{align}
\begin{align} &(1-M)\left(l_{top,0}+\frac{W_{bot}}{h^*}\right)+M(W_{top}+h^{*3}W_{bot})+l_{eff,l}+Ml_{eff,r}\nonumber\\ &\quad+(h^{*3}-1)(1-M)l_{bot}=\frac{\sigma(\cos{\theta_{top}}-h^*\cos{\theta_{bot}})h^*h_{top}}{6\mu_{inv}} \boldsymbol{\cdot}\frac{1}{u_{bot}}. \end{align}
The only parameters in (3.9) that need fitting are the geometry-dependent ![]() $l_{eff,l}$ and
$l_{eff,l}$ and ![]() $l_{eff,r}$, which represent the effective channel lengths due to the curved channels at the left and right sides, indicated by the purple and orange dashed curves in figure 3, respectively. Figure 4(c) shows the term
$l_{eff,r}$, which represent the effective channel lengths due to the curved channels at the left and right sides, indicated by the purple and orange dashed curves in figure 3, respectively. Figure 4(c) shows the term ![]() $l_{eff,l}+M \cdot l_{eff,r}$ as a function of the viscosity ratio
$l_{eff,l}+M \cdot l_{eff,r}$ as a function of the viscosity ratio ![]() $M$ for all nine cases listed in table 1, and the fitted values are
$M$ for all nine cases listed in table 1, and the fitted values are ![]() $l_{eff,l}=1.4$ mm and
$l_{eff,l}=1.4$ mm and ![]() $l_{eff,r}=7.9$ mm, where fitting was done using the default least-squares algorithm available in the fit function in MATLAB. The strong linear trend with a coefficient of determination
$l_{eff,r}=7.9$ mm, where fitting was done using the default least-squares algorithm available in the fit function in MATLAB. The strong linear trend with a coefficient of determination ![]() $R^2=0.999$ evidences that
$R^2=0.999$ evidences that ![]() $l_{eff,l}$ and
$l_{eff,l}$ and ![]() $l_{eff,r}$ are indeed fluid-property-independent. This means that, once these parameters are fitted (model calibration process), (3.9) can be used to describe processes with different fluid properties without the need for further fitting.
$l_{eff,r}$ are indeed fluid-property-independent. This means that, once these parameters are fitted (model calibration process), (3.9) can be used to describe processes with different fluid properties without the need for further fitting.
To quantify the error induced by ignoring the inlet velocity in the model, figure 4(b) plots the relative error in estimating the top meniscus location using the bottom one based on mass conservation without taking into account the additional invading fluid injected from the inlet during Haines jumps. The relative error is calculated by the absolute error in meniscus location divided by the total distance travelled during Haines jumps. As expected, the error decreases with the average bottom meniscus velocity during Haines jumps. The maximum error occurs when the meniscus velocity is minimum (case 5), leading to an error of around 0.3 mm. However, this error is still less than 10 % of the distance travelled by the bottom meniscus during Haines jumps (a relative error of less than 0.1 in figure 4b).
To validate (3.9), figure 4(d) compares the value of ![]() $u_{bot}$ obtained from numerical simulation and
$u_{bot}$ obtained from numerical simulation and ![]() $u_{bot}$ calculated from (3.9), showing a good agreement. The markers in yellow appear to be a single point on figure 4(d). This is because the overlaps of
$u_{bot}$ calculated from (3.9), showing a good agreement. The markers in yellow appear to be a single point on figure 4(d). This is because the overlaps of ![]() $u_{bot}$ that remain constant during Haines jumps due to the viscosity ratio
$u_{bot}$ that remain constant during Haines jumps due to the viscosity ratio ![]() $M=1$.
$M=1$.
3.4. Simultaneous determination of viscosity and interfacial tension
By examining (3.9), we notice that, apart from the fluid property-related terms ![]() $M$ and
$M$ and ![]() $\sigma /\mu _{inv}$, all other parameters can be determined from the geometry (
$\sigma /\mu _{inv}$, all other parameters can be determined from the geometry (![]() $W_{bot}$,
$W_{bot}$, ![]() $W_{top}$,
$W_{top}$, ![]() $h_{bot}$,
$h_{bot}$, ![]() $h_{top}$,
$h_{top}$, ![]() $l_{eff,l}$,
$l_{eff,l}$, ![]() $l_{eff,r}$) or measured during the Haines jump process (
$l_{eff,r}$) or measured during the Haines jump process (![]() $l_{bot}$,
$l_{bot}$, ![]() $u_{bot}$,
$u_{bot}$, ![]() $\cos {\theta _{bot}}$,
$\cos {\theta _{bot}}$, ![]() $\cos {\theta _{top}}$). As a result, the values of
$\cos {\theta _{top}}$). As a result, the values of ![]() $M$ and
$M$ and ![]() $\sigma /\mu _{inv}$ can be determined by analysing the dynamics of meniscus movement during Haines jumps. In the case where, for example, the defending fluid viscosity
$\sigma /\mu _{inv}$ can be determined by analysing the dynamics of meniscus movement during Haines jumps. In the case where, for example, the defending fluid viscosity ![]() $\mu _{def}$ is known, the interfacial tension
$\mu _{def}$ is known, the interfacial tension ![]() $\sigma$ and viscosity of the invading fluid
$\sigma$ and viscosity of the invading fluid ![]() $\mu _{inv}$ can be simultaneously calculated using (3.9) based on the measured bottom meniscus location, velocity and contact angles at the bottom and top channel during the Haines jumps.
$\mu _{inv}$ can be simultaneously calculated using (3.9) based on the measured bottom meniscus location, velocity and contact angles at the bottom and top channel during the Haines jumps.
Figure 5 shows the comparisons between predicted values of fluid properties and the respective true values (marker legend meaning is the same as figure 4a). The error bars represent one standard deviation considering the uncertainties from: (i) measurement uncertainty from simulation results, including the fluctuations in the measured advancing and receding contact angles and uncertainty in interface location (i.e. the difference between the locations of the interface tip along the channel centre and the triple-contact lines); (ii) fitting uncertainty in the fitted values of ![]() $l_{eff,l}$ and
$l_{eff,l}$ and ![]() $l_{eff,r}$ with confidence interval 0.68; and (iii) model error, which is induced from the assumption that the inlet velocity can be ignored during the Haines jump (as discussed in the previous section and figure 4b). Further, the corresponding relative errors in figure 5(a–c), calculated as
$l_{eff,r}$ with confidence interval 0.68; and (iii) model error, which is induced from the assumption that the inlet velocity can be ignored during the Haines jump (as discussed in the previous section and figure 4b). Further, the corresponding relative errors in figure 5(a–c), calculated as ![]() $|\text {true-predicted}|/\text {true}$, are plotted in figure 5(d–f). We see that the relative errors become greater as the viscosity ratio
$|\text {true-predicted}|/\text {true}$, are plotted in figure 5(d–f). We see that the relative errors become greater as the viscosity ratio ![]() $M$ deviates from unity, leading to a relative error in the predicted
$M$ deviates from unity, leading to a relative error in the predicted ![]() $\mu _{inv}$ as large as 0.59 for
$\mu _{inv}$ as large as 0.59 for ![]() $M=0.1$. This reveals that the intrinsic errors (aforementioned measurement uncertainty, fitting uncertainty and model assumption) are magnified as the fluid viscosity contrast is greater. Nevertheless, the relative errors in the surface tension prediction remain less than 10 % in the range
$M=0.1$. This reveals that the intrinsic errors (aforementioned measurement uncertainty, fitting uncertainty and model assumption) are magnified as the fluid viscosity contrast is greater. Nevertheless, the relative errors in the surface tension prediction remain less than 10 % in the range ![]() $M\in [0.1,10]$. Note that the results in figure 5(d,e) are identical, since figure 5(a,b) essentially contains the same information scaled by
$M\in [0.1,10]$. Note that the results in figure 5(d,e) are identical, since figure 5(a,b) essentially contains the same information scaled by ![]() $\mu _{def}$.
$\mu _{def}$.

Figure 5. Simultaneous determination of fluid properties during a Haines jump. (a) Viscosity ratio ![]() $M$, (b) viscosity of the invading fluid
$M$, (b) viscosity of the invading fluid ![]() $\mu _{inv}$ and (c) interfacial tension. Refer to the legend in figure 4(a) for marker meaning. (d–f) The corresponding relative errors of the predicted values on the top panels as a function of the viscosity ratio.
$\mu _{inv}$ and (c) interfacial tension. Refer to the legend in figure 4(a) for marker meaning. (d–f) The corresponding relative errors of the predicted values on the top panels as a function of the viscosity ratio.
3.5. Effect of channel depth
In previous sections, we have focused on 2-D cases corresponding to a channel geometry with a depth ![]() $D$ much greater than the width
$D$ much greater than the width ![]() $h$, such that the calculation of permeability is simplified to
$h$, such that the calculation of permeability is simplified to ![]() $k=h^2/12$ according to (3.5). Practically, such microfluidic devices can be manufactured using the selective laser etching technique (Gottmann, Hermans & Ortmann Reference Gottmann, Hermans and Ortmann2012), an example of which is the porous medium micromodel with a depth-to-post diameter ratio of 20 (Haward, Hopkins & Shen Reference Haward, Hopkins and Shen2021). However, in other conventional methods for microfluidic device fabrication, such as soft lithography, the aspect ratio may not be so large and the effect of channel depth cannot be ignored. In such cases, the permeability is calculated using (3.5). As (3.5) quickly converges as the number of terms
$k=h^2/12$ according to (3.5). Practically, such microfluidic devices can be manufactured using the selective laser etching technique (Gottmann, Hermans & Ortmann Reference Gottmann, Hermans and Ortmann2012), an example of which is the porous medium micromodel with a depth-to-post diameter ratio of 20 (Haward, Hopkins & Shen Reference Haward, Hopkins and Shen2021). However, in other conventional methods for microfluidic device fabrication, such as soft lithography, the aspect ratio may not be so large and the effect of channel depth cannot be ignored. In such cases, the permeability is calculated using (3.5). As (3.5) quickly converges as the number of terms ![]() $N$ increases,
$N$ increases, ![]() $N=5$ is used for the calculation of permeability, where a less than 0.1 % variation is observed as
$N=5$ is used for the calculation of permeability, where a less than 0.1 % variation is observed as ![]() $N$ further increases.
$N$ further increases.
To quantitatively explore the effect of channel depth on the flow in the dual-channel system, we define the aspect ratio ![]() $\beta =D/h_{bot}$. The average bottom meniscus velocity
$\beta =D/h_{bot}$. The average bottom meniscus velocity ![]() $\overline {u_{bot}}$ normalised by the injection velocity
$\overline {u_{bot}}$ normalised by the injection velocity ![]() $V_{in}$ is plotted as a function of
$V_{in}$ is plotted as a function of ![]() $\beta$ in figure 6. The fluid properties of case 7 are used for calculation. The black-dashed line and red-dot-dashed line, respectively, represent the meniscus velocity for the 2-D case (
$\beta$ in figure 6. The fluid properties of case 7 are used for calculation. The black-dashed line and red-dot-dashed line, respectively, represent the meniscus velocity for the 2-D case (![]() $\beta \rightarrow \infty$) and the injection velocity
$\beta \rightarrow \infty$) and the injection velocity ![]() $V_{in}=1$ mm s
$V_{in}=1$ mm s![]() $^{-1}$ in the simulation. The meniscus velocity decreases from its maximum as
$^{-1}$ in the simulation. The meniscus velocity decreases from its maximum as ![]() $\beta$ decreases, reaching below the currently imposed
$\beta$ decreases, reaching below the currently imposed ![]() $V_{in}$ at
$V_{in}$ at ![]() $\beta =0.1$. This means that a much smaller injection velocity is required to ensure that the speed of interface motion during Haines jumps is much greater than
$\beta =0.1$. This means that a much smaller injection velocity is required to ensure that the speed of interface motion during Haines jumps is much greater than ![]() $V_{in}$. In rectangular channels, aspect ratios
$V_{in}$. In rectangular channels, aspect ratios ![]() $\beta$ of 10, 1 and 0.1 lead to the actual permeability (and meniscus velocity) being 94 %, 42 % and 1 % of the value for a 2-D scenario (
$\beta$ of 10, 1 and 0.1 lead to the actual permeability (and meniscus velocity) being 94 %, 42 % and 1 % of the value for a 2-D scenario (![]() $\beta \rightarrow \infty$). This highlights that a large aspect ratio is desired whereas a small aspect ratio can lead to a drastic reduction of meniscus velocity.
$\beta \rightarrow \infty$). This highlights that a large aspect ratio is desired whereas a small aspect ratio can lead to a drastic reduction of meniscus velocity.

Figure 6. The average bottom meniscus movement velocity ![]() $\overline {u_{bot}}$ during Haines jumps normalised by the inlet velocity
$\overline {u_{bot}}$ during Haines jumps normalised by the inlet velocity ![]() $V_{in}$ under different
$V_{in}$ under different ![]() $\beta$. The black-dashed line represents the 2-D scenario.
$\beta$. The black-dashed line represents the 2-D scenario.
3.6. Discussion
In the design of the dual-channel system as well as the numerical simulations, we have considered drainage processes for which the contact angle is greater than ![]() $90^\circ$. However, we emphasise that the same analysis, namely the competition between viscous and capillary forces, can also be applied to imbibition processes (
$90^\circ$. However, we emphasise that the same analysis, namely the competition between viscous and capillary forces, can also be applied to imbibition processes (![]() $\theta <90^\circ )$. Similarly, it is possible to design dual-channel geometries with different channel widths and the placement of barriers to create hierarchies of capillary pressures. Although Haines jumps are commonly referred to in drainage processes, the same physical phenomenon, i.e. rapid fluid interface motion accompanied by liquid redistribution and pressure fluctuations, are also present in imbibition processes (Zhao, MacMinn & Juanes Reference Zhao, MacMinn and Juanes2016; Primkulov et al. Reference Primkulov, Zhao, MacMinn and Juanes2022).
$\theta <90^\circ )$. Similarly, it is possible to design dual-channel geometries with different channel widths and the placement of barriers to create hierarchies of capillary pressures. Although Haines jumps are commonly referred to in drainage processes, the same physical phenomenon, i.e. rapid fluid interface motion accompanied by liquid redistribution and pressure fluctuations, are also present in imbibition processes (Zhao, MacMinn & Juanes Reference Zhao, MacMinn and Juanes2016; Primkulov et al. Reference Primkulov, Zhao, MacMinn and Juanes2022).
An important requirement for the applicability of the current approach is the existence of the actuation force that originates from the differences in capillary pressure between the top and bottom menisci (described in (3.1)). However, the contact angle hysteresis ![]() $\theta '=\theta _{adv}-\theta _{rec}$, i.e. the difference between the advancing (bottom side) and receding (top side) contact angles, can lead to deviations of effective contact angles from the equilibrium ones, which hinders the driving capillary force. In the current work, the contact angle hysteresis in the simulation is small, i.e. the difference between
$\theta '=\theta _{adv}-\theta _{rec}$, i.e. the difference between the advancing (bottom side) and receding (top side) contact angles, can lead to deviations of effective contact angles from the equilibrium ones, which hinders the driving capillary force. In the current work, the contact angle hysteresis in the simulation is small, i.e. the difference between ![]() $\theta _{top}$ and
$\theta _{top}$ and ![]() $\theta _{bot}$ (or the difference between
$\theta _{bot}$ (or the difference between ![]() $\theta _{rec}$ and
$\theta _{rec}$ and ![]() $\theta _{adv}$) is less than
$\theta _{adv}$) is less than ![]() $3^\circ$. In practical applications, the contact angle hysteresis can be greater due to surface chemical heterogeneity or roughness. Reducing contact angle hysteresis on engineered surfaces has been an active area of research. For example, Esmaeilzadeh et al. (Reference Esmaeilzadeh, Sadeghi, Bahramian, Fakhroueian and Zarbakhsh2016) showed that the contact angle hysteresis can be reduced to less than
$3^\circ$. In practical applications, the contact angle hysteresis can be greater due to surface chemical heterogeneity or roughness. Reducing contact angle hysteresis on engineered surfaces has been an active area of research. For example, Esmaeilzadeh et al. (Reference Esmaeilzadeh, Sadeghi, Bahramian, Fakhroueian and Zarbakhsh2016) showed that the contact angle hysteresis can be reduced to less than ![]() $5^\circ$ by surface coating of nanoparticles.
$5^\circ$ by surface coating of nanoparticles.
To ensure a positive capillary driving force with consideration of contact angle hysteresis, the critical channel width contrast ![]() $h^*_{crit}$ should satisfy
$h^*_{crit}$ should satisfy
where ![]() $\cos {\theta _{top}=\theta -\theta '/2}$,
$\cos {\theta _{top}=\theta -\theta '/2}$, ![]() $\cos {\theta _{bot}=\theta +\theta '/2}$ and
$\cos {\theta _{bot}=\theta +\theta '/2}$ and ![]() $\beta =D/h_{bot}$ represents the aspect ratio of the channel. The contour maps for
$\beta =D/h_{bot}$ represents the aspect ratio of the channel. The contour maps for ![]() $h^*_{crit}$ under different
$h^*_{crit}$ under different ![]() $\beta$ are plotted in figure 7. Here, we consider a practical range of
$\beta$ are plotted in figure 7. Here, we consider a practical range of ![]() $h^*_{crit}\in [0.1, 10]$. The white region in figure 7 represents the region where the Haines jump cannot take place. It can be seen that the minimum channel contrast is more demanding as: (i) contact angle hysteresis increases; (ii) when the equilibrium contact angle
$h^*_{crit}\in [0.1, 10]$. The white region in figure 7 represents the region where the Haines jump cannot take place. It can be seen that the minimum channel contrast is more demanding as: (i) contact angle hysteresis increases; (ii) when the equilibrium contact angle ![]() $\theta$ approaches the neutral condition (
$\theta$ approaches the neutral condition (![]() $\theta =90^\circ$); or (iii) the aspect ratio
$\theta =90^\circ$); or (iii) the aspect ratio ![]() $\beta$ decreases, which is associated with the increasing effect of contact angle hysteresis from the out-of-plane direction. Thus, ensuring homogeneous solid surfaces for small contact angle hysteresis, as well as a non-neutral solid wettability, are critical when manufacturing the physical device. Note that the asymmetry in the contour maps for finite values of
$\beta$ decreases, which is associated with the increasing effect of contact angle hysteresis from the out-of-plane direction. Thus, ensuring homogeneous solid surfaces for small contact angle hysteresis, as well as a non-neutral solid wettability, are critical when manufacturing the physical device. Note that the asymmetry in the contour maps for finite values of ![]() $\beta$ is due to the definition of the aspect ratio being based on the bottom channel width.
$\beta$ is due to the definition of the aspect ratio being based on the bottom channel width.

Figure 7. Effect of contact angle hysteresis. Contour map showing the critical width contrast ![]() $h^*_c$ required for Haines jumps as a function of equilibrium contact angle and contact angle hysteresis for (a)
$h^*_c$ required for Haines jumps as a function of equilibrium contact angle and contact angle hysteresis for (a) ![]() $\beta \to \infty$ (corresponding to the 2-D case), (b)
$\beta \to \infty$ (corresponding to the 2-D case), (b) ![]() $\beta =1$ and (c)
$\beta =1$ and (c) ![]() $\beta =0.2$.
$\beta =0.2$.
Overall, our results (figure 5) highlight that the dual-channel configuration combined with the developed model in the work can provide an effective approach to simultaneously measuring the interfacial tension and fluid viscosity in a multiphase system. Despite acknowledging the existing advanced techniques for fluid property testing, such as those that require force sensing equipment during droplet merger (Nguyen et al. Reference Nguyen, Okada, Okamoto, Takei, Takei and Ichiki2021), laser-light scattering apparatus (Nishio & Nagasaka Reference Nishio and Nagasaka1995) or oscillations of acoustically levitated droplets (Kremer, Kilzer & Petermann Reference Kremer, Kilzer and Petermann2018) combined with rainbow refractometry (Wu et al. Reference Wu, Lv, Wu, Wang, Chen and Cen2021) or under a microgravity environment (Fujii et al. Reference Fujii, Matsumoto, Ueda and Nogi2005), we want to highlight the key advantages of the present approach. Firstly, such a method only requires the imaging of the fluid distribution and control of the injection velocity, which is straightforward compared with existing techniques and does not require advanced equipment. Further, the fluid properties are determined by analysing the Haines jump phenomena that occur ubiquitously in fluid–fluid displacement processes in a confined geometry. This means that it is possible to extend the theory for in situ fluid property characterisation during multiphase flow in an artificial porous medium that has regular pore structures, where the capillary driving force and viscous dissipation can be accurately quantified. Such non-intrusive real-time characterisation of the fluid property could be particularly important in processes where fluid flow is accompanied by chemical reaction/mass transport (Dudukovic et al. Reference Dudukovic, Fong, Gemeda, DeOtte, Cerón, Moran, Davis, Baker and Duoss2021; Wang et al. Reference Wang, Ong, Gan, Pereira, Zhang, Kasetsirikul, Toh and Sauret2024).
4. Conclusions
Inspired by the Haines jump mechanisms commonly observed during immiscible fluid displacement processes in porous media, we have designed a dual-channel system with hierarchies of capillary barriers to realise the spontaneous rapid liquid redistribution during multiphase flow. Three regimes of the interface motion behaviours are identified, where the meniscus movement velocity can increase, decrease or remain the same during Haines jumps, depending on the viscosity ratio of the invading and defending fluids. Based on the competition between capillary and viscous forces, an analytical model is developed to describe the dynamics of interface movement during Haines jumps. Results from numerical simulations under different viscosities, surface tensions and contact angles show that the proposed analytical model can well describe the interfacial movement. Further, our analysis demonstrates that the dual-channel system combined with the developed model is capable of simultaneously determining the interfacial tension and fluid viscosity. This work provides fundamental insights into multiphase flow processes, and the results should facilitate the development of alternative approaches for the effective measurement of important fluid properties.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2024.1225.
Acknowledgements
The authors thank the anonymous reviewers for their constructive feedback.
Funding
This work was supported by the Queensland University of Technology (QUT) MMPE Early Career Researcher (ECR) grant awarded to Z.W., and the Australian Research Council Future Fellowship FT200100446 awarded to E.S.
Declaration of interests
The authors declare no competing interests.