Published online by Cambridge University Press: 07 August 2023
The formation process of the leading vortex ring in starting jets with uniform background co- and counter-flow has been studied numerically for  $-0.5\leq R_v\leq 0.5$, where
$-0.5\leq R_v\leq 0.5$, where  $R_v$ is the ratio of background velocity to jet velocity. For the cases with background counter-flow, the normal formation process of the leading vortex ring would be destroyed when
$R_v$ is the ratio of background velocity to jet velocity. For the cases with background counter-flow, the normal formation process of the leading vortex ring would be destroyed when  $R_v<-0.4$, i.e. the trailing jet would overtake the leading vortex ring through the centre, a phenomenon reminiscent of vortex leapfrogging. As the velocity ratio
$R_v<-0.4$, i.e. the trailing jet would overtake the leading vortex ring through the centre, a phenomenon reminiscent of vortex leapfrogging. As the velocity ratio  $R_v$ increases, the formation number
$R_v$ increases, the formation number  $F_{t^*}$ decreases from
$F_{t^*}$ decreases from  $9.6$ at
$9.6$ at  $R_v=-0.4$ to
$R_v=-0.4$ to  $1.92$ at
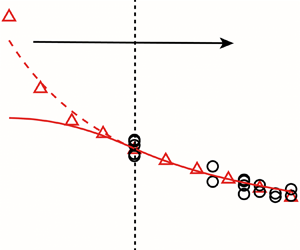
$1.92$ at  $R_v=0.5$. An analytical model based on the kinematic criterion has been developed so as to describe the relationship between the formation number
$R_v=0.5$. An analytical model based on the kinematic criterion has been developed so as to describe the relationship between the formation number  $F_{t^*}$ and velocity ratio
$F_{t^*}$ and velocity ratio  $R_v$. A linear relationship between the vortex core parameter and stroke ratio of starting jet (
$R_v$. A linear relationship between the vortex core parameter and stroke ratio of starting jet ( $\varepsilon \sim k_1L/D$) for the Norbury vortex ring has been established and used effectively to close the model. For co-flow with
$\varepsilon \sim k_1L/D$) for the Norbury vortex ring has been established and used effectively to close the model. For co-flow with  $0< R_v\leq 0.5$, the results from this model are consistent with the present numerical simulation and the experiments by Krueger et al. (J. Fluid Mech., vol. 556, 2006, pp. 147–166). For counter-flow, two different equations are proposed for
$0< R_v\leq 0.5$, the results from this model are consistent with the present numerical simulation and the experiments by Krueger et al. (J. Fluid Mech., vol. 556, 2006, pp. 147–166). For counter-flow, two different equations are proposed for  $-0.4\leq R_v\leq -0.2$ and
$-0.4\leq R_v\leq -0.2$ and  $-0.2< R_v<0$, respectively.
$-0.2< R_v<0$, respectively.