Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T17:15:23.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Structural sensitivity of spiral vortex breakdown

Published online by Cambridge University Press:  27 February 2013

Ubaid Ali Qadri ,
Dhiren Mistry  and
Matthew P. Juniper
Ubaid Ali Qadri*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
Dhiren Mistry
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
Matthew P. Juniper
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Previous numerical simulations have shown that vortex breakdown starts with the formation of a steady axisymmetric bubble and that an unsteady spiralling mode then develops on top of this. We investigate this spiral mode with a linear global stability analysis around the steady bubble and its wake. We obtain the linear direct and adjoint global modes of the linearized Navier–Stokes equations and overlap these to obtain the structural sensitivity of the spiral mode, which identifies the wavemaker region. We also identify regions of absolute instability with a local stability analysis. 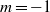At moderate swirls, we find that the $m= - 1$ azimuthal mode is the most unstable and that the wavemaker regions of the 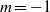$m= - 1$ mode lie around the bubble, which is absolutely unstable. The mode is most sensitive to feedback involving the radial and azimuthal components of momentum in the region just upstream of the bubble. To a lesser extent, the mode is also sensitive to feedback involving the axial component of momentum in regions of high shear around the bubble. At an intermediate swirl, in which the bubble and wake have similar absolute growth rates, other researchers have found that the wavemaker of the nonlinear global mode lies in the wake. We agree with their analysis but find that the regions around the bubble are more influential than the wake in determining the growth rate and frequency of the linear global mode. The results from this paper provide the first steps towards passive control strategies for spiral vortex breakdown.

JFM classification

Instability: Instability Vortex Flows: Vortex breakdown Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 558 - 581
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14 (4), 593–629.Google Scholar
Chandler, G. J., Juniper, M. P., Nichols, J. W. & Schmid, P. J. 2012 Adjoint algorithms for the Navier–Stokes equations in the low Mach number limit. J. Comput. Phys. 231 (4), 1900–1916.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Constantinescu, G. S. & Lele, S. K. 2002 A highly accurate technique for the treatment of flow equations at the polar axis in cylindrical coordinates using series expansions. J. Comput. Phys. 183 (1), 165–186.CrossRefGoogle Scholar
Escudier, M. 1988 Vortex breakdown: observations and explanations. Prog. Aero. Sci. 25 (2).Google Scholar
Gallaire, F., Ruith, M., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Grabowski, W. J. & Berger, S. A. 1976 Solutions of Navier–Stokes equations for vortex breakdown. J. Fluid Mech. 75, 525–544.CrossRefGoogle Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4, 195–218.Google Scholar
Heaton, C. J., Nichols, J. W. & Schmid, P. J. 2009 Global linear stability of the non-parallel Batchelor vortex. J. Fluid Mech. 629, 139–160.CrossRefGoogle Scholar
Hill, D. C. 1992 A theoretical approach for analysing the re-stabilization of wakes. AIAA Paper 92-0067.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Juniper, M. P., Tammisola, O. & Lundell, F. 2011 The local and global stability of confined planar wakes at intermediate Reynolds number. J. Fluid Mech. 686, 218–238.Google Scholar
Lambourne, N. C. & Bryer, D. W. 1961 The bursting of leading-edge vortices – some observations and discussion of the phenomenon. Aero. Res. Counc. R & M 3282.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicity Restarted Arnoldi Methods. SIAM.Google Scholar
Leibovich, S. 1978 Structure of vortex breakdown. Annu. Rev. Fluid Mech. 10, 221–246.Google Scholar
Leibovich, S. & Stewartson, K. 1983 A sufficient condition for the instability of columnar vortices. J. Fluid Mech. 126, 335–356.Google Scholar
Lucca-Negro, O. & O’Doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27, 431–481.CrossRefGoogle Scholar
Ludwieg, H. 1960 Stabilitat der Stromung in einem zylindrischen Ringraum. Z. Flugwiss. 8 (5), 135–140.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Meliga, P. & Gallaire, F. 2011 Global instability of helical vortex breakdown. In 6th AIAA Theoretical Fluid Mechanics Conference, 27–30 June 2011, Honolulu, Hawaii.Google Scholar
Meliga, P., Gallaire, F. & Chomaz, J.-M. 2012 A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid. Mech 699, 216–262.Google Scholar
Meliga, P., Sipp, D. & Chomaz, J.-M. 2010 Open-loop control of compressible afterbody flows using adjoint methods. Phys. Fluids 22 (5), 054109.CrossRefGoogle Scholar
Nichols, J. W., Schmid, P. J. & Riley, J. J. 2007 Self-sustained oscillations in variable-density round jets. J. Fluid Mech. 582, 341–376.Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H.-C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid. Mech 679, 383–414.Google Scholar
Peckham, D. H. & Atkinson, S. A. 1957 Preliminary results of low speed wind tunnel tests on a gothic wing of aspect ratio 1.0. Aero. Res. Counc. Tech. Rep..Google Scholar
Pier, B., Huerre, P. & Chomaz, J.-M. 2001 Bifurcation to fully nonlinear synchronized structures in slowly varying media. Physica D 148, 49–96.Google Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.CrossRefGoogle Scholar
Spall, R. & Snyder, D. 1999 Numerical simulations of vortex breakdown: review and recent developments. Recent Res. Dev. Heat, Mass Momentum Transfer 2, 41–70.Google Scholar
Tammisola, O. 2012 Oscillatory sensitivity patterns for global modes in wakes. J. Fluid Mech. 701, 251–277.Google Scholar
Vyazmina, E., Nichols, J. W., Chomaz, J.-M. & Schmid, P. J. 2009 The bifurcation structure of viscous steady axisymmetric vortex breakdown with open lateral boundaries. Phys. Fluids 21, 074107.CrossRefGoogle Scholar