Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T23:34:07.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability, sensitivity and optimisation of chaotic acoustic oscillations

Published online by Cambridge University Press:  11 November 2019

Francisco Huhn Open the ORCID record for Francisco Huhn [Opens in a new window]  and
Luca Magri Open the ORCID record for Luca Magri [Opens in a new window]
Francisco Huhn
Affiliation:
Cambridge University Engineering Department, Trumpington Street, Cambridge CB2 1PZ, UK
Luca Magri*
Affiliation:
Cambridge University Engineering Department, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

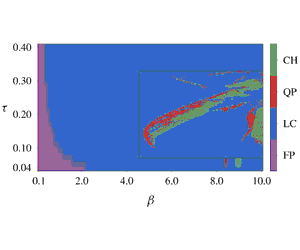
In an acoustic cavity with a heat source, such as a flame in a gas turbine, the thermal energy of the heat source can be converted into acoustic energy, which may generate a loud oscillation. If uncontrolled, these nonlinear acoustic oscillations, also known as thermoacoustic instabilities, can cause large vibrations up to structural failure. Numerical and experimental studies showed that thermoacoustic oscillations can be chaotic. It is not yet known, however, how to minimise such chaotic oscillations. We propose a strategy to analyse and minimise chaotic acoustic oscillations, for which traditional stability and sensitivity methods break down. We investigate the acoustics of a nonlinear heat source in an acoustic resonator. First, we propose covariant Lyapunov analysis as a tool to calculate the stability of chaotic acoustics, making connections with eigenvalue and Floquet analyses. We show that covariant Lyapunov analysis is the most general flow stability tool. Second, covariant Lyapunov vector analysis is applied to a chaotic system. The time-averaged acoustic energy is investigated by varying the heat-source parameters. Thermoacoustic systems can display both hyperbolic and non-hyperbolic chaos, as well as discontinuities in the time-averaged acoustic energy. Third, we embed sensitivities of the time-averaged acoustic energy in an optimisation routine. This procedure achieves a significant reduction in acoustic energy and identifies the bifurcations to chaos. The analysis and methods proposed enable the reduction of chaotic oscillations in thermoacoustic systems by optimal passive control. The techniques presented can be used in other unsteady fluid-dynamics problems with virtually no modification.

JFM classification

Instability: Nonlinear instability Nonlinear Dynamical Systems: Chaos
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 882 , 10 January 2020 , A24
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aguilar, J. & Juniper, M. P. 2018 Adjoint methods for elimination of thermoacoustic oscillations in a model annular combustor via small geometry modifications. In Turbo Expo: Power for Land, Sea, and Air, ASME Turbo Expo, Oslo, Norway, vol. 4A Combustion, Fuels, and Emissions. ASME.Google Scholar
Balasubramanian, K. & Sujith, R. I. 2008 Thermoacoustic instability in a Rijke tube: non-normality and nonlinearity. Phys. Fluids 20 (4), 044103.Google Scholar
Birkhoff, G. D. 1931 Proof of the ergodic theorem. Proc. Natl Acad. Sci. USA 17 (12), 656–660.Google Scholar
Blonigan, P. J. 2017 Adjoint sensitivity analysis of chaotic dynamical systems with non-intrusive least squares shadowing. J. Comput. Phys. 348, 803–826.Google Scholar
Blonigan, P. J., Fernandez, P., Murman, S. M., Wang, Q., Rigas, G. & Magri, L. 2016 Towards a chaotic adjoint for LES. In Center for Turbulence Research, Summer Program, Stanford University.Google Scholar
Blonigan, P. J. & Wang, Q. 2014 Least squares shadowing sensitivity analysis of a modified Kuramoto-Sivashinsky equation. Chaos, Solitons Fractals 64 (1), 16–25.Google Scholar
Blumenthal, R. S., Tangirala, A. K., Sujith, R. & Polifke, W. 2016 A systems perspective on non-normality in low-order thermoacoustic models: full norms, semi-norms and transient growth. Intl J. Spray Combustion Dynamics 9 (1), 19–43.Google Scholar
Bowen, R. & Ruelle, D. 1975 The ergodic theory of Axiom A flows. Invent. Math. 29, 181–202.Google Scholar
Chu, B. T. 1965 On the energy transfer to small disturbances in fluid flow (Part I). Acta Mechanica 1 (3), 215–234.Google Scholar
Culick, F. E. C. 2006 Unsteady Motions in Combustion Chambers for Propulsion Systems. RTO AGARDograph AG-AVT-039, North Atlantic Treaty Organization.Google Scholar
Curtain, R. F. & Zwart, H. 1995 An Introduction to Infinite-Dimensional Linear Systems Theory, vol. 21. Springer.Google Scholar
Dowling, A. P. 1997 Nonlinear self-excited oscillations of a ducted flame. J. Fluid Mech. 346, 271–290.Google Scholar
Dowling, A. P. 1999 A kinematic model of a ducted flame. J. Fluid Mech. 394, 51–72.Google Scholar
Dowling, A. P. & Mahmoudi, Y. 2015 Combustion noise. Proc. Combust. Inst. 35 (1), 65–100.Google Scholar
Dowling, A. P. & Morgans, A. S. 2005 Feedback control of combustion oscillations. Annu. Rev. Fluid Mech. 37, 151–182.Google Scholar
Eckmann, J.-P. 1981 Roads to turbulence in dissipative dynamical systems. Rev. Mod. Phys. 53 (4), 643–654.Google Scholar
Eckmann, J. P. & Ruelle, D. 1985 Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 57, 617–656.Google Scholar
Eyink, G. L., Haine, T. W. N. & Lea, D. J. 2004 Ruelle’s linear response formula, ensemble adjoint schemes and Lévy flights. Nonlinearity 17 (5), 1867–1889.Google Scholar
Fernandez, P. & Wang, Q. 2017 Lyapunov spectrum of the separated flow around the NACA 0012 airfoil and its dependence on numerical discretization. J. Comput. Phys. 350, 453–469.Google Scholar
Gallavotti, G. 2006 Entropy, thermostats, and chaotic hypothesis. Chaos 16 (4), 043114.Google Scholar
Gallavotti, G. & Cohen, E. G. D. 1995 Dynamical ensembles in stationary states. J. Stat. Phys. 80 (5–6), 931–970.Google Scholar
George, K. J. & Sujith, R. I. 2012 Disturbance energy norms: a critical analysis. J. Sound Vib. 331 (7), 1552–1566.Google Scholar
Ginelli, F., Chaté, H., Livi, R. & Politi, A. 2013 Covariant Lyapunov vectors. J. Phys. A: Math. Theoret. 46 (25), 254005.Google Scholar
Ginelli, F., Poggi, P., Turchi, A., Chaté, H., Livi, R. & Politi, A. 2007 Characterizing dynamics with covariant Lyapunov vectors. Phys. Rev. Lett. 99 (13), 130601.Google Scholar
Gotoda, H., Ikawa, T., Maki, K. & Miyano, T. 2012 Short-term prediction of dynamical behavior of flame front instability induced by radiative heat loss. Chaos 22 (1), 033106.Google Scholar
Gotoda, H., Nikimoto, H., Miyano, T. & Tachibana, S. 2011 Dynamic properties of combustion instability in a lean premixed gas-turbine combustor. Chaos 21 (1), 013124.Google Scholar
Guckenheimer, J. & Holmes, P. 1983 Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer.Google Scholar
Heckl, M. A. 1988 Active control of the noise from a Rijke tube. J. Sound Vib. 124 (1), 117–133.Google Scholar
Heckl, M. A. 1990 Non-linear acoustic effects in the Rijke tube. Acustica 72, 63–71.Google Scholar
Holmes, P., Lumley, J. L. & Berzook, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.Google Scholar
Inubushi, M., Takehiro, S.-i & Yamada, M. 2015 Regeneration cycle and the covariant lyapunov vectors in a minimal wall turbulence. Phys. Rev. E 92, 023022.Google Scholar
Jarlebring, E.2008 The spectrum of delay-differential equations: numerical methods, stability and perturbation. KTH Royal Institute of Technology.Google Scholar
Juniper, M. P. 2011 Triggering in the horizontal Rijke tube: non-normality, transient growth and bypass transition. J. Fluid Mech. 667, 272–308.Google Scholar
Juniper, M. P. & Sujith, R. I. 2018 Sensitivity and nonlinearity of thermoacoustic oscillations. Annu. Rev. Fluid Mech. 50 (1), 661–689.Google Scholar
Kabiraj, L., Saurabh, A., Wahi, P. & Sujith, R. I. 2012 Route to chaos for combustion instability in ducted Laminar premixed flames. Chaos 22 (2), 0–12.Google Scholar
Kabiraj, L., Sujith, R. I. & Wahi, P. 2011 Bifurcations of self-excited ducted laminar premixed flames. J. Engng Gas Turbines Power 134 (3), 31502.Google Scholar
Kashinath, K., Hemchandra, S. & Juniper, M. P. 2013a Nonlinear phenomena in thermoacoustic systems with premixed flames. Trans. ASME J. Engng Gas Turbines Power 135 (6), 061502.Google Scholar
Kashinath, K., Hemchandra, S. & Juniper, M. P. 2013b Nonlinear thermoacoustics of ducted premixed flames: the influence of perturbation convection speed. Combust. Flame 160 (12), 2856–2865.Google Scholar
Kashinath, K., Waugh, I. C. & Juniper, M. P. 2014 Nonlinear self-excited thermoacoustic oscillations of a ducted premixed flame: bifurcations and routes to chaos. J. Fluid Mech. 761, 399–430.Google Scholar
Katok, A. & Hasselblatt, B. 1995 Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press.Google Scholar
King, L. V. 1914 On the convection of heat from small cyclinders in a stream of fluid: determination of the convection constants of small platinum wires with applications to hot-wire anemometry. Proc. R. Soc. Lond. A 214 (8), 373–434.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Pergamon Press.Google Scholar
Lea, D. J., Allen, M. R. & Haine, T. W. N. 2000 Sensitivity analysis of the climate of a chaotic system. Tellus 52 (5), 523–532.Google Scholar
Lieuwen, T. 2012 Unsteady Combustor Physics. Cambridge University Press.Google Scholar
Lieuwen, T. C. & Yang, V. 2005 Combustion Instabilities in Gas Turbine Engines: Operational Experience, Fundamental Mechanisms, and Modeling. American Institute of Aeronautics and Astronautics, Inc.Google Scholar
Magri, L.2015 Adjoint methods in thermo-acoustic and combustion instability. PhD thesis, University of Cambridge.Google Scholar
Magri, L. 2018 Adjoint methods as design tools in thermoacoustics. Appl. Mech. Rev. 71 (2), 020801.Google Scholar
Magri, L., Bauerheim, M., Nicoud, F. & Juniper, M. P. 2016 Stability analysis of thermo-acoustic nonlinear eigenproblems in annular combustors. Part II. Uncertainty quantification. J. Comput. Phys. 325, 411–421.Google Scholar
Magri, L. & Juniper, M. P. 2013 Sensitivity analysis of a time-delayed thermo-acoustic system via an adjoint-based approach. J. Fluid Mech. 719, 183–202.Google Scholar
Magri, L. & Juniper, M. P. 2014 Global modes, receptivity, and sensitivity analysis of diffusion flames coupled with duct acoustics. J. Fluid Mech. 752, 237–265.Google Scholar
Mensah, G. A., Magri, L. & Moeck, J. P. 2018 Methods for the calculation of thermoacoustic stability margins and Monte-Carlo free uncertainty quantification. Trans. ASME J. Engng Gas Turbines Power 140 (6), 061501.Google Scholar
Mensah, G. A. & Moeck, J. P. 2017 Acoustic damper placement and tuning for annular combustors: an adjoint-based optimization study. Trans. ASME J. Engng Gas Turbines Power 139 (6), 061501.Google Scholar
Miles, J. 1984 Strange attractors in fluid dynamics. Adv. Appl. Mech. 24, 189–214.Google Scholar
Nair, V. & Sujith, R. I. 2015 A reduced-order model for the onset of combustion instability: physical mechanisms for intermittency and precursors. Proc. Combust Inst. 35 (3), 3193–3200.Google Scholar
Nair, V., Thampi, G. & Sujith, R. I. 2014 Intermittency route to thermoacoustic instability in turbulent combustors. J. Fluid Mech. 756, 470–487.Google Scholar
Ni, A. 2019 Hyperbolicity, shadowing directions and sensitivity analysis of a turbulent three-dimensional flow. J. Fluid Mech. 863, 644–669.Google Scholar
Ni, A. & Wang, Q. 2017 Sensitivity analysis on chaotic dynamical systems by non-intrusive least squares shadowing (NILSS). J. Comput. Phys. 347, 56–77.Google Scholar
Orchini, a., Illingworth, S. J. & Juniper, M. P. 2015 Frequency domain and time domain analysis of thermoacoustic oscillations with wave-based acoustics. J. Fluid Mech. 775, 387–414.Google Scholar
Orchini, A., Rigas, G. & Juniper, M. P. 2016 Weakly nonlinear analysis of thermoacoustic bifurcations in the Rijke tube. J. Fluid Mech. 805, 523–550.Google Scholar
Oseledets, V. I. 1968 A multiplicative ergodic theorem: Lyapunov characteristic numbers for dynamical systems. Trans. Moscow Math. Soc. 19, 197–231.Google Scholar
Petzold, L. 1983 Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations. SIAM J. Sci. Stat. Comput. 4 (1), 136–148.Google Scholar
Pilyugin, S. Y. 2006 Shadowing in Dynamical Systems. Springer.Google Scholar
Poinsot, T. 2017 Prediction and control of combustion instabilities in real engines. Proc. Combust. Inst. 36 (1), 1–28.Google Scholar
Polifke, W., Poncet, A., Paschereit, C. O. & Döbbeling, K. 2001 Reconstruction of acoustic transfer matrices by instationary computational fluid dynamics. J. Sound Vib. 245 (3), 483–510.Google Scholar
Rayleigh, Lord 1878 The explanation of certain acoustical phenomena. Nature 18 (455), 319–321.Google Scholar
Ruelle, D. 1980 Measures describing a turbulent flow. Ann. N.Y. Acad. Sci. 357 (1), 1–9.Google Scholar
Ruelle, D. 2009 A review of linear response theory for general differentiable dynamical systems. Nonlinearity 22 (4), 855.Google Scholar
Schubert, S. & Lucarini, V. 2015 Covariant lyapunov vectors of a quasi-geostrophic baroclinic model: analysis of instabilities and feedbacks. Q. J. R. Meteorol. Soc. 141 (693), 3040–3055.Google Scholar
Silva, C. F., Magri, L., Runte, T. & Polifke, W. 2016 Uncertainty quantification of growth rates of thermoacoustic instability by an adjoint Helmholtz solver. Trans. ASME J. Engng Gas Turbines Power 139 (1), 011901.Google Scholar
Subramanian, P., Mariappan, S., Sujith, R. I. & Wahi, P. 2011 Bifurcation analysis of thermoacoustic instability in a horizontal Rijke tube. Intl J. Spray Combust. Dyn. 2 (4), 325–355.Google Scholar
Subramanian, P. & Sujith, R. I. 2011 Non-normality and internal flame dynamics in premixed flame-acoustic interaction. J. Fluid Mech. 679 (2011), 315–342.Google Scholar
Takeuchi, K. A., Yang, H.-l., Ginelli, F., Radons, G. & Chaté, H. 2011 Hyperbolic decoupling of tangent space and effective dimension of dissipative systems. Phys. Rev. E 84, 046214.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB, vol. 10. SIAM.Google Scholar
Trevisan, A. & Pancotti, F. 1998 Periodic orbits, Lyapunov vectors, and singular vectors in the Lorenz system. J. Atmos. Sci. 55 (3), 390–398.Google Scholar
Tyagi, M., Jamadar, N. & Chakravarthy, S. 2007 Oscillatory response of an idealized two-dimensional diffusion flame: analytical and numerical study. Combust. Flame 149 (3), 271–285.Google Scholar
Wang, Q. 2013 Forward and adjoint sensitivity computation of chaotic dynamical systems. J. Comput. Phys. 235, 1–13.Google Scholar
Wang, Q., Hu, R. & Blonigan, P. 2014 Least squares shadowing sensitivity analysis of chaotic limit cycle oscillations. J. Comput. Phys. 267, 210–224.Google Scholar
Waugh, I. C., Kashinath, K. & Juniper, M. P. 2014 Matrix-free continuation of limit cycles and their bifurcations for a ducted premixed flame. J. Fluid Mech. 759, 1–27.Google Scholar
Xu, M. & Paul, M. R. 2016 Covariant Lyapunov vectors of chaotic Rayleigh–Bénard convection. Phys. Rev. E 93 (6), 1–12.Google Scholar
Yu, H., Juniper, M. P. & Magri, L. 2019 Combined state and parameter estimation in level-set methods. J. Comput. Phys. 399, 108950.Google Scholar
Zinn, B. T. & Lores, M. E. 1971 Application of the Galerkin method in the solution of non-linear axial combustion instability problems in liquid rockets. Combust. Sci. Technol. 4 (1), 269–278.Google Scholar