Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T22:13:57.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Shape effects on turbulent modulation by large nearly neutrally buoyant particles

Published online by Cambridge University Press:  27 September 2012

Gabriele Bellani ,
Margaret L. Byron ,
Audric G. Collignon ,
Colin R. Meyer  and
Evan A. Variano
Gabriele Bellani*
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA Linné Flow Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
Margaret L. Byron
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA
Audric G. Collignon
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA
Colin R. Meyer
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA
Evan A. Variano
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate dilute suspensions of Taylor-microscale-sized particles in homogeneous isotropic turbulence. In particular, we focus on the effect of particle shape on particle–fluid interaction. We conduct laboratory experiments using a novel experimental technique to simultaneously measure the kinematics of fluid and particle phases. This uses transparent particles having the same refractive index as water, whose motion we track via embedded optical tracers. We compare the turbulent statistics of a single-phase flow to the turbulent statistics of the fluid phase in a particle–laden suspension. Two suspensions are compared, one in which the particles are spheres and the other in which they are prolate ellipsoids with aspect ratio 2. We find that spherical particles at volume fraction 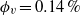${\phi }_{v} = 0. 14\hspace{0.167em} \% $ reduce the turbulent kinetic energy (TKE) by 15 % relative to the single-phase flow. At the same volume fraction (and slightly smaller total surface area), ellipsoidal particles have a much smaller effect: they reduce the TKE by 3 % relative to the single-phase flow. Spectral analysis shows the details of TKE reduction and redistribution across spatial scales: spherical particles remove energy from large scales and reinsert it at small scales, while ellipsoids remove relatively less TKE from large scales and reinsert relatively more at small scales. Shape effects are far less evident in the statistics of particle rotation, which are very similar for ellipsoids and spheres. Comparing these with fluid enstrophy statistics, we find that particle rotation is dominated by velocity gradients on scales much larger than the particle characteristic length scales.

JFM classification

Turbulent Flows: Homogeneous turbulence Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 712 , 10 December 2012 , pp. 41 - 60
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496–3513.CrossRefGoogle Scholar
Bagchi, P. & Balachandar, S. 2004 Response of the wake of an isolated particle to an isotropic turbulent flow. J. Fluid Mech. 518, 95–123.CrossRefGoogle Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Bellani, G. 2011 Experimental studies of complex flows through image-based techniques. PhD thesis, Royal Institute of Technology, Stockholm.Google Scholar
Bellani, G. & Variano, E. A. 2012 Slip-velocity and drag of large neutrally-buoyant particles in turbulent flows. New J. Phys. arXiv:1207.7142.CrossRefGoogle Scholar
Bendat, J. S. & Piersol, A. G. 2010 Random Data: Analysis and Measurement Procedures. John Wiley and Sons.CrossRefGoogle Scholar
Benzi, R., Angelis, E. D., L’vov, V. S. & Procaccia, I. 2005 Identification and calculation of the universal asymptote for drag reduction by polymers in wall bounded turbulence. Phys. Rev. Lett. 95.CrossRefGoogle ScholarPubMed
Burton, T. M. & Eaton, J. K. 2005 Fully resolved simulations of particle-turbulence interaction. J. Fluid Mech. 545, 67–111.CrossRefGoogle Scholar
Calzavarini, E., Volk, R., Lévêque, E., Pinton, J. & Toschi, F. 2012 Impact of trailing wake drag on the statistical properties and dynamics of finite-sized particle in turbulence. Physica D 241, 237–244.CrossRefGoogle Scholar
Clamen, A. & Gauvin, W. H. 1969 Effects of turbulence on the drag coefficients of spheres in a supercritical flow ŕegime. AIChE J. 15 (2), 184–189.CrossRefGoogle Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops, and Particles. Academic.Google Scholar
Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3 (5), 1169–1178.Google Scholar
Eaton, J. K. 2009 Two-way coupled turbulence simulations of gas-particle flows using point-particle tracking. Intl J. Multiphase Flow 35 (9), 792–800.CrossRefGoogle Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52, 309–329.CrossRefGoogle Scholar
Elghobashi, S. 2003 On the physical mechanisms of two-way coupling in particle-laden isotropic turbulence. Phys. Fluids 15 (2), 315–329.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1993 On the two way interaction between homogeneous turbulence and dispersed solid particles. I. Turbulence modification. Phys. Fluids A 5, 1790–1801.CrossRefGoogle Scholar
El Khoury, G. K., Andersson, H. I. & Pettersen, B. 2010 Crossflow past a prolate spheroid at Reynolds number of 10 000. J. Fluid Mech. 659, 365–374.CrossRefGoogle Scholar
Ferrante, A. & Elghobashi, S. 2004 On the physical mechanisms of drag reduction in a spatially developing turbulent boundary layer laden with microbubbles. J. Fluid Mech. 503, 345–355.CrossRefGoogle Scholar
Garcia, M. H. 2008 Sedimentation Engineering: Theories, Measurements, Modeling and Practice: Processes, Management, Modelling, and Practice, 1st edn. American Society of Civil Engineers.CrossRefGoogle Scholar
Geiss, S., Dreizler, A., Stojanovic, Z. & Chrigui, M. 2004 Investigation of turbulence modification in a non-reactive two-phase flow. Exp. Fluids 36, 344–354.CrossRefGoogle Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 161–179.Google Scholar
Jumars, P. A., Trowbridge, J. H., Boss, E. & Karp-Boss, L. 2009 Turbulence-plankton interactions: a new cartoon. Mar. Ecol. 30 (2), 133–150.CrossRefGoogle Scholar
Kim, I., Elghobashi, S. & Sirignano, W. A. 1998 On the equation for spherical-particle motion: effect of Reynolds and acceleration numbers. J. Fluid Mech. 367, 221–253.CrossRefGoogle Scholar
Koch, D. L. & Shaqfeh, E. S. G. 1989 The instability of a dispersion of sedimenting spheroids. J. Fluid Mech. 209, 521–542.CrossRefGoogle Scholar
Liberzon, A., Guala, M., Lüthi, B. & Kinzelbach, W. 2005 Turbulence in dilute polymer solutions. Phys. Fluids 17, 031707.CrossRefGoogle Scholar
Loth, E. 2008 Drag of non-spherical solid particles of regular and irregular shape. Powder Technol. 182, 342–353.CrossRefGoogle Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.CrossRefGoogle Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2011 Is stokes number an appropriate indicator for turbulence modulation by particles of Taylor-length-scale size? Phys. Fluids 23 (2), 025101.CrossRefGoogle Scholar
Lundell, F. 2011 The effect of particle inertia on triaxial ellipsoids in creeping shear: from drift toward chaos to a single periodic solution. Phys. Fluids 23 (1), 011704.CrossRefGoogle Scholar
Lundell, F., Söderberg, L. D. & Alfredsson, P. H. 2010 Fluid mechanics of papermaking. Annu. Rev. Fluid Mech. 43, 195–217.CrossRefGoogle Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–890.CrossRefGoogle Scholar
Moradian, N., Ting, D. S.-K. & Cheng, S. 2009 The effects of freestream turbulence on the drag coefficient of a sphere. Exp. Therm. Fluid Sci. 33 (3), 460–471.CrossRefGoogle Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2007 Particle spin in a turbulent shear flow. Phys. Fluids 19, 078109.CrossRefGoogle Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008a Dynamics of prolate ellipsoidal particles in a turbulent channel flow. Phys. Fluids 20, 0933202.CrossRefGoogle Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008b On the orientation of ellipsoidal particles in a turbulent shear flow. Intl J. Multiphase Flow 34, 678–683.CrossRefGoogle Scholar
Ouellette, N. T., O’Malley, P. J. J. & Gollub, J. P. 2008 Transport of finite-sized particles in chaotic flow. Phys. Rev. Lett. 101 (17), 174504.CrossRefGoogle ScholarPubMed
Poelma, C., Westerweel, J. & Ooms, G. 2006 Turbulence statistics from optical whole-field measurements in particle-laden turbulence. Exp. Fluids 40, 347–363.CrossRefGoogle Scholar
Poelma, C., Westerweel, J. & Ooms, G. 2007 Particle–fluid interactions in grid-generated turbulence. J. Fluid Mech. 589, 315–351.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Qureshi, N. M., Bourgoin, M., Baudet, C., Cartellier, A. & Gagne, Y. 2007 Turbulent transport of material particles: an experimental study of finite size effects. Phys. Rev. Lett. 99 (18), 184502–4.CrossRefGoogle ScholarPubMed
Sabban, L. & Van Hout, R. 2011 Measurements of pollen grain dispersal in still air and stationary, near homogeneous, isotropic turbulence. J. Aerosol Sci. 42 (12), 867–882.CrossRefGoogle Scholar
Saw, E. W., Shaw, R. S., Ayyalasomayajula, S., Chuang, P. Y. & Gylfason, A. 2008 Inertial clustering of particles in high-Reynolds-number turbulence. Phys. Rev. Lett. 100 (21), 214501–214505.CrossRefGoogle ScholarPubMed
Schreck, S. & Kleis, S. J. 1993 Modification of grid-generated turbulence by solid particles. J. Fluid Mech. 249, 665–688.CrossRefGoogle Scholar
Squires, K. D. & Eaton, J. K. 1990 Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A 2, 1191–1203.CrossRefGoogle Scholar
Tanaka, T. & Eaton, J. K. 2010 Sub-kolmogorov resolution partical image velocimetry measurements of particle-laden forced turbulence. J. Fluid Mech. 643, 177–206.CrossRefGoogle Scholar
Tsinober, A. 2004 An Informal Introduction to Turbulence. Kluwer.Google Scholar
Variano, E. A. & Cowen, E. A. 2008 A random-jet-stirred turbulence tank. J. Fluid Mech. 604, 1–32.CrossRefGoogle Scholar
Virk, P. S., Merrill, E. W., Mickley, H. S. & Smith, K. A. 1967 The toms phenomenon: turbulent pipe flow of dilute polymer solutions. J. Fluid Mech. 30, 305–328.CrossRefGoogle Scholar
Xu, H. & Bodenschatz, E. 2008 Motion of inertial particles with size larger than kolmogorov scale in turbulent flows. Physica D 237 (14–17), 2095–2100.CrossRefGoogle Scholar
Yang, T. S. & Shy, S. S. 2005 Two-way interaction between solid particles and homogeneous air turbulence: particle settling rate and turbulence modification measurements. J. Fluid Mech. 526, 171–216.CrossRefGoogle Scholar
Yeo, K., Dong, S., Climent, E. & Maxey, M. R. 2010 Modulation of homogeneous turbulence seeded with finite size bubbles or particles. Intl J. Multiphase Flow 36 (3), 221–233.CrossRefGoogle Scholar
Zastawny, M., Mallouppas, G., Zhao, F. & van Wachem, B. 2012 Derivation of drag and lift force and torque coefficients for non-spherical particles in flows. Intl J. Multiphase Flow 39, 227–239.CrossRefGoogle Scholar
Zhang, H., Ahmadi, G., Fan, F. G. & McLaughlin, J. B. 2001 Ellipsoidal particles transport and deposition in turbulent channel flows. Intl J. Multiphase Flow 27 (6), 971–1009.CrossRefGoogle Scholar
Zhao, L. & Andersson, H. I. 2011 On particle spin in two-way coupled turbulent channel flow simulations. Phys. Fluids 23, 093302.CrossRefGoogle Scholar