Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T19:36:10.783Z Has data issue: false hasContentIssue false
  • English
  • Français

Sedimentation from binary suspensions in a turbulent gravity current along a V-shaped valley

Published online by Cambridge University Press:  13 September 2012

Catherine A. Mériaux  and
Cathy B. Kurz-Besson
Catherine A. Mériaux*
Affiliation:
Instituto Dom Luiz, Departamento de Engenharia Geografica, Geofisica e Energia, Faculdade de Ciências, Universidade de Lisboa, Campo Grande 1749-016 Lisboa, Portugal
Cathy B. Kurz-Besson
Affiliation:
Instituto Dom Luiz, Departamento de Engenharia Geografica, Geofisica e Energia, Faculdade de Ciências, Universidade de Lisboa, Campo Grande 1749-016 Lisboa, Portugal
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a study of bidispersed particulate gravity currents at high Reynolds numbers flowing along a V-shaped valley. The speed and width of the currents, the mass deposited by the currents and the density of the deposits were examined by both a box model and lock-exchange experiments in a 5 m long tank. Silicon carbide and glass beads were used for the bidispersed suspension models. The initial conditions of the currents were similar, except that the grain size of the glass beads was successively chosen to be 2, 2.5 and 4 times that of the silicon carbide. For all experiments a Stokes’ settling velocity model, assuming that both particles are spherical, gives a settling rate of the glass beads that is greater than that of the silicon carbide by a factor ranging from 1.6 to 16.5. When the ratio of the Stokes’ settling velocity of the glass beads to that of the silicon carbide is greater than ∼6, we find a complete agreement between the box model and the experiment. In particular, the deposit shows a substantial decline in the mass of the coarser glass beads in the first metre, so that it only contains the finer silicon carbide further downstream. By contrast, when the Stokes’ settling velocity ratio is less than ∼4, only the speed of the current and the total sedimented mass can be well described by the box model. The experimental deposit is otherwise characterized by a slightly increasing density, which the box model fails to match. There is no difference in the deposit density across the valley. 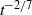For all experiments in the V-shaped valley, the width of the currents decreases with time $t$ according to ${t}^{\ensuremath{-} 2/ 7} $. Analogue experiments in a flat-bottom tank were also performed to assess the influence of the valley on the sedimentation dynamics described above. A similar behaviour with settling velocity ratios was found. This study eventually shows the need for considering particle interactions in even dilute gravity currents at high Reynolds numbers.

JFM classification

Waves/Free-surface Flows: Channel flow Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Sediment transport
Type
Papers
Information
Journal of Fluid Mechanics , Volume 712 , 10 December 2012 , pp. 624 - 645
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baas, J. H., McCaffery, W. D., Haughton, P. D. W. & Choux, C. 2005 Coupling between suspended sediment distribution and turbulence structure in a laboratory turbidity current. J. Geophys. Res. 110, doi:10.1029/2004JC002668.Google Scholar
Batchelor, G. K. 1982 Sedimentation in a dilute polydisperse system of interacting spheres. Part 1. General theory. J. Fluid Mech. 119, 379–408.Google Scholar
Bonnecaze, R. T., Huppert, H. E. & Lister, J. R. 1996 Patterns of sedimentation from polydispersed turbidity currents. Proc. R. Soc. Lond. A 452, 2247–2261.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic.Google Scholar
Choux, C. M. & Druitt, T. H. 2002 Analogue study of particle segregation in pyroclastic density currents, with implications for the emplacement mechanisms of large ignimbrites. Sedimentology 49, 907–928.CrossRefGoogle Scholar
Choux, C., Druitt, T. & Thomas, N. 2004 Stratification and particle segregation in flowing polydisperse suspensions, with applications to the transport and sedimentation of pyroclastic density currents. J. Volcanol. Geotherm. Res. 138, 223–241.Google Scholar
Dade, W. B. & Huppert, H. E. 1996 Emplacement of the Taupo ignimbrite by a dilute turbulent flow. Nature 381, 509–512.Google Scholar
Davis, R. H. & Acrivos, A. 1985 Sedimentation of noncolloidal particles at low Reynolds number. Annu. Rev. Fluid Mech. 17, 91–118.Google Scholar
Dietrich, W. E. 1982 Settling velocity of natural particles. Water Resour. Res. 18, 1615–1626.Google Scholar
Eaton, J. K. & Flessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Einstein, A. 1906 A new determination of the molecular dimensions. Ann. Phys. 19 (2), 289–306.Google Scholar
Garcia, M. H. 1994 Depositional turbidity currents laden with poorly sorted sediment. J. Hydraul. Engng ASCE 120, 1240–1263.Google Scholar
Gladstone, C., Phillips, J. C. & Sparks, R. S. J. 1998 Experiments on bidisperse, constant-volume gravity currents: propagation and sediment deposition. Sedimentology 45, 833–843.Google Scholar
Hodson, J. M. & Alexander, J. 2010 The effects of grain-density variation on turbidity currents and some implications for the deposition of carbonate turbidites. J. Sedim. Res. 80, 515–528.Google Scholar
Huang, H., Imran, J. & Pirmez, C. 2007 Numerical modelling of poorly sorted depositional turbidity currents. J. Geophys. Res. 112, doi:10.1029/2006JC003778.Google Scholar
Kneller, B. & Buckee, C. 2000 The structure and fluid mechanics of turbidity currents: a review of some recent studies and their geological implication. Sedimentology 47 (Suppl. 1), 62–94.Google Scholar
McCaffrey, W. D., Choux, C. M., Baas, J. H. & Haughton, P. D. W. 2003 Spatio-temporal evolution of velocity structure, concentration and grain-size stratification within experimental particulate gravity currents. Mar. Petrol. Geol. 20, 851–860.Google Scholar
Martin, D. & Nokes, R. 1988 A fluid-dynamical study of crystal settling in convecting magmas. Nature 332, 534–536.Google Scholar
Martin, D. & Nokes, R. 1989 A fluid-dynamical study of crystal settling in convecting magmas. J. Petrol. 30, 1471–1500.Google Scholar
Meiburg, E. & Kneller, B. 2010 Turbidity currents and their deposits. Annu. Rev. Fluid Mech. 42, 135–156.Google Scholar
Monaghan, J. J., Mériaux, C. A., Huppert, H. E. & Monaghan, J. M. 2009a High Reynolds number gravity currents along V-shaped valleys. Eur. J. Mech. (B/Fluids 28, 651–659.CrossRefGoogle Scholar
Monaghan, J. J., Mériaux, C. A., Huppert, H. E. & Mansour, J. 2009b Particulate gravity currents along V-shaped valleys. J. Fluid Mech. 631, 419–440.Google Scholar
Salaheldina, T. M., Imrana, J., Chaudhrya, M. H. & Reed, C. 2000 Role of fine-grained sediment in turbidity current flow dynamics and resulting deposits. Mar. Geol. 171, 21–38.Google Scholar
Sparks, R. S. J. 1976 Grain size variations in ignimbrites and implications for the transport of pyroclastic flows. Sedimentology 23, 147–188.Google Scholar
Wang, L. P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar