No CrossRef data available.
Article contents
Reynolds number dependence of turbulent kinetic energy and energy balance of 3-component turbulence intensity in a pipe flow
Published online by Cambridge University Press: 10 November 2023
Abstract
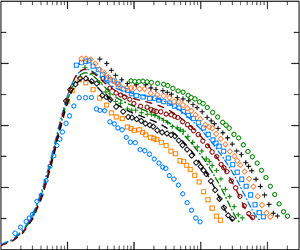
Measurement data sets are presented for the turbulence intensity profile of three velocity components (
$u$, 
$v$ and 
$w$) and turbulent kinetic energy (TKE, 
$k$) over a wide range of Reynolds numbers from 
$Re_\tau =990$ to 20 750 in a pipe flow. The turbulence intensity profiles of the 
$u$- and 
$w$-component show logarithmic behaviour, and that of the 
$v$-component shows a constant region at high Reynolds numbers, 
$Re_\tau >10\,000$. Furthermore, a logarithmic region is also observed in the TKE profile at 
$y/R=0.055\unicode{x2013}0.25$. The Reynolds number dependences of peak values of 
$u$-, 
$w$-component and TKE fit to both a logarithmic law (Marusic et al., Phys. Rev. Fluids, vol. 2, 2017, 100502) and an asymptotic law (Chen and Sreenivasan, J. Fluid Mech., vol. 908, 2020, R3), within the uncertainty of measurement. The Reynolds number dependence of the bulk TKE 
$k^+_{bulk}$, which is the total amount of TKE in the cross-sectional area of the pipe also fits to both laws. When the asymptotic law is applied to the 
$k^+_{bulk}$, it asymptotically increases to the finite value 
$k^+_{bulk}=11$ as the Reynolds number increases. The contribution ratio 
$\langle u'^2\rangle /k$ reaches a plateau, and the value tends to be constant within 
$100< y^+<1000$ at 
$Re_\tau >10\ 000$. Therefore, the local balance of each velocity component also indicates asymptotic behaviour. The contribution ratios are balanced in this region at high Reynolds numbers as 
$\langle u'^2\rangle /k\simeq 1.25$, 
$\langle w'^2\rangle /k\simeq 0.5$ and 
$\langle v'^2\rangle /k \simeq 0.25$.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
Abe, H. & Antonia, R.A. 2011 Scaling of normalized mean energy and scalar dissipation ratios in a turbulent channel flow. Phys. Fluids 25, 055104.CrossRefGoogle Scholar
Ahn, J., Lee, J.H., Lee, J., Kang, J. & Sung, H.J. 2015 Direct numerical simulation of a 30R long turbulent pipe flow at 
$Re= 3008$. Phys. Fluids 27, 065110.CrossRefGoogle Scholar
$Re= 3008$. Phys. Fluids 27, 065110.CrossRefGoogle ScholarAlbrecht, H.E., Borys, M., Damascheke, N. & Tropea, C. 2002 Laser Doppler and Phase Doppler Measurement Techniques. Springer.Google Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J.P. & Marusic, I. 2021 Spanwise velocity statistics in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 913, A35.CrossRefGoogle Scholar
Chen, X. & Sreenivasan, K.R. 2020 Reynolds number scaling of the peak turbulence intensity in wall flows. J. Fluid Mech. 908, R3.CrossRefGoogle Scholar
Chen, X. & Sreenivasan, K.R. 2022 Law of bounded dissipation and its consequences in turbulent wall flows. J. Fluid Mech. 933, A20.CrossRefGoogle Scholar
Chin, C., Monty, J.P. & Ooi, A. 2014 Reynolds number effects in DNS of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.CrossRefGoogle Scholar
Cho, M., Hwang, Y. & Choi, H. 2018 Scale interactions and spectral energy transfer in turbulent channel flow. J. Fluid Mech. 854, 474–504.CrossRefGoogle Scholar
Den Toonder, J.M.J. & Nieuwstadt, F.T.M. 1997 Reynolds number effects in a turbulent pipe flow for low to moderate Re. Phys. Fluids 9, 3398–3409.CrossRefGoogle Scholar
Durst, F., Jovanović, J. & Sender, J. 1995 LDA measurements in the near-wall region of a turbulent pipe flow. J. Fluid Mech. 295, 305–335.CrossRefGoogle Scholar
Fu, M.K., Fan, Y. & Hultmark, M. 2019 Design and validation of a nanoscale cross-wire probe (X-NSTAP). Exp. Fluids 60 (6), 1–14.CrossRefGoogle Scholar
Furuichi, N., Terao, Y., Wada, Y. & Tsuji, Y. 2015 Friction factor and mean velocity profile for pipe flow at high Reynolds numbers. Phys. Fluids 27, 095108.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S.C.C. & Smits, A.J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Laufer, J. 1954 The structure of turbulence in fully developed pipe flow. National Advisory Committee for Aeronautics. Tech. Rep., vol. 1174, pp. 417–434.Google Scholar
Lee, M. & Moser, R.D. 2015 Direct numerical simulation of turbulent channel flow up to $Re_\tau =5200$. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
$Re_\tau =5200$. J. Fluid Mech. 774, 395–415.CrossRefGoogle ScholarMarusic, I., Baars, W.J. & Hutchins, N. 2017 Scaling of the streamwise turbulence intensity in the context of inner-outer interactions in wall turbulence. Phys. Rev. Fluids 2, 100502.CrossRefGoogle Scholar
Marusic, I., Monty, J.P., Hultmark, M. & Smits, A.J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Monkewitz, P.A. 2021 The late start of the mean velocity overlap log law at-a generic feature of turbulent wall layers in ducts. J. Fluid Mech. 910, 1–28.CrossRefGoogle Scholar
Ono, M., Furuichi, N., Kurihara, N., Wada, Y. & Tsuji, Y. 2022 Reynolds number dependence of inner peak turbulence intensity in pipe flow. Phys. Fluids 34, 045103.CrossRefGoogle Scholar
Örlü, R., Fiorini, T., Segalini, A., Bellani, G., Talamelli, A. & Alfredsson, P.H. 2017 Reynolds stress scaling in pipe flow turbulence – first results from CICLoPE. Phil. Trans. R. Soc. A 375, 20160187.CrossRefGoogle ScholarPubMed
Perry, A.E. & Chong, M.S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Pirozzoli, S., Romero, J., Fatica, M., Verzicco, R. & Orlandi, P. 2021 One-point statistics for turbulent pipe flow up to $Re_\tau \approx 6000$. J. Fluid Mech. 926, A28.CrossRefGoogle Scholar
$Re_\tau \approx 6000$. J. Fluid Mech. 926, A28.CrossRefGoogle ScholarRenard, N. & Deck, S. 2016 A theoretical decomposition of mean skin friction generation into physical phenomena across the boundary layer. J. Fluid Mech. 790, 339–367.CrossRefGoogle Scholar
Samie, M., Marusic, I., Hutchins, N., Fu, M.K., Fan, Y., Hultmark, M. & Smits, A.J. 2018 Fully resolved measurements of turbulent boundary layer flows up to $Re_\tau =20\,000$. J. Fluid Mech. 851, 391–415.CrossRefGoogle Scholar
$Re_\tau =20\,000$. J. Fluid Mech. 851, 391–415.CrossRefGoogle ScholarSchiavo, L.A.C.A., Wolf, W.R. & Azevedo, J.L.F. 2017 Turbulent kinetic energy budgets in wall bounded flows with pressure gradients and separation. Phys. Fluids 29, 115108.CrossRefGoogle Scholar
Sillero, J.A., Jiménez, J. & Moser, R.D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to $\delta \approx 2000$. Phys. Fluids 25, 105102.CrossRefGoogle Scholar
$\delta \approx 2000$. Phys. Fluids 25, 105102.CrossRefGoogle ScholarSreenivasan, K.R. & Sahay, A. 1997 The persistence of viscous effects in the overlap region, and the mean velocity in turbulent pipe and channel flows. Adv. Fluid Mech. 15, 253–270.Google Scholar
Townsend, A.A. 1951 The structure of the turbulent boundary layer. Math. Proc. Camb. Philos. Soc. 47, 375–395.CrossRefGoogle Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vallikivi, M., Hultmark, M. & Smits, A.J. 2015 Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.CrossRefGoogle Scholar
Wei, T. 2018 Integral properties of turbulent-kinetic-energy production and dissipation in turbulent wall-bounded flows. J. Fluid Mech. 854, 449–473.CrossRefGoogle Scholar
Wei, T. 2020 Scaling of turbulent kinetic energy and dissipation in turbulent wall-bounded flows. Phys. Rev. Fluids 5, 94602.CrossRefGoogle Scholar
Willert, C.E., Soria, J., Stanislas, M., Klinner, J., Amili, O., Eisfelder, M., Cuvier, C., Bellani, G., Fiorini, T. & Talamelli, A. 2017 Near-wall statistics of a turbulent pipe flow at shear Reynolds numbers up to 40 000. J. Fluid Mech. 826, R5.CrossRefGoogle Scholar
Wu, X. & Moin, P. 2008 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar
Yamamoto, Y. & Tsuji, Y. 2018 Numerical evidence of logarithmic regions in channel flow at $Re_\tau =8000$. Phys. Rev. Fluids s 3, 012602(R).CrossRefGoogle Scholar
$Re_\tau =8000$. Phys. Rev. Fluids s 3, 012602(R).CrossRefGoogle ScholarYao, J., Rezaeiravesh, S., Schlatter, P. & Hussain, F. 2023 Direct numerical simulation of turbulent pipe flow up to $Re_\tau =5200$. J. Fluid Mech. 956, A18.CrossRefGoogle Scholar
$Re_\tau =5200$. J. Fluid Mech. 956, A18.CrossRefGoogle ScholarZhao, R. & Smits, A.J. 2007 Scaling of the wall-normal turbulence component in high-Reynolds-number pipe flow. J. Fluid Mech. 576, 457–473.CrossRefGoogle Scholar
Zimmerman, S., et al. 2019 A comparative study of the velocity and vorticity structure in pipes and boundary layers at friction Reynolds numbers up to $10^4$. J. Fluid Mech. 869, 182–213.CrossRefGoogle Scholar
$10^4$. J. Fluid Mech. 869, 182–213.CrossRefGoogle Scholar