Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-11T12:01:06.704Z Has data issue: false hasContentIssue false
  • English
  • Français

The non-resonant response of fluid in a rapidly rotating sphere undergoing longitudinal libration

Published online by Cambridge University Press:  27 February 2013

Keke Zhang ,
Kit H. Chan ,
Xinhao Liao  and
Jonathan M. Aurnou
Keke Zhang*
Affiliation:
Department of Mathematical Sciences, University of Exeter, Exeter EX4 4QF, UK
Kit H. Chan
Affiliation:
Department of Mathematics, University of Hong Kong, Pokfulam, Hong Kong
Xinhao Liao
Affiliation:
Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China
Jonathan M. Aurnou
Affiliation:
Department of Earth and Space Sciences, University of California, Los Angeles, CA 90095-1567, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the problem of oscillatory flow of a homogeneous fluid with viscosity $\nu $ in a fluid-filled sphere of radius $a$ that rotates rapidly about a fixed axis with angular velocity 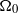${\Omega }_{0} $ and that undergoes weak longitudinal libration with amplitude 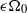$\epsilon {\Omega }_{0} $ and frequency 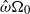$\hat {\omega } {\Omega }_{0} $, where $\epsilon $ is the Poincaré number with 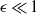$\epsilon \ll 1$ and 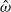$\hat {\omega } $ is dimensionless frequency with 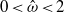$0\lt \hat {\omega } \lt 2$. Three different methods are employed in this investigation: (i) asymptotic analysis at small Ekman numbers 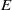$E$ defined as 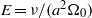$E= \nu / ({a}^{2} {\Omega }_{0} )$; (ii) linear numerical analysis using a spectral method; and (iii) nonlinear direct numerical simulation using a finite-element method. A satisfactory agreement among the three different sets of solutions is achieved when 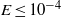$E\leq 1{0}^{- 4} $. It is shown that the flow amplitude 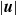$\vert \boldsymbol{u}\vert $ is nearly independent of both the Ekman number 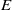$E$ and the libration frequency 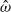$\hat {\omega } $, always obeying the asymptotic scaling 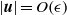$\vert \boldsymbol{u}\vert = O(\epsilon )$ even though various spherical inertial modes are excited by longitudinal libration at different libration frequencies 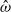$\hat {\omega } $. Consequently, resonances do not occur in this system even when 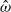$\hat {\omega } $ is at the characteristic value of an inertial mode. It is also shown that the pressure difference along the axis of rotation is anomalous: this quantity reaches a sharp peak when 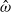$\hat {\omega } $ approaches a characteristic value. In contrast, the pressure difference measured at other places in the sphere, such as in the equatorial plane, and the volume-integrated kinetic energy are nearly independent of both the Ekman number 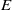$E$ and the libration frequency 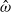$\hat {\omega } $. Absence of resonances in a fluid-filled sphere forced by longitudinal libration is explained through the special properties of the analytical solution that satisfies the no-slip boundary condition and is valid for 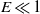$E\ll 1$ and 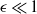$\epsilon \ll 1$.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 212 - 235
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldridge, K. D. & Toomre, A. 1969 Axisymmetric inertial oscillations of a fluid in a rotating spherical container. J. Fluid Mech. 37, 307–323.Google Scholar
Busse, F. H. 1968 Steady fluid flow in a precessing spheroidal shell. J. Fluid Mech. 136, 739–751.CrossRefGoogle Scholar
Busse, F. H. 2010 Mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 650, 505–512.Google Scholar
Calkins, M. A., Noir, J., Eldredge, J. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22, 086602.CrossRefGoogle Scholar
Cébron, D., Le Bars, M., Noir, J. & Aurnou, J. M. 2012 Libration driven elliptical instability. Phys. Fluids 24, 061703.CrossRefGoogle Scholar
Chan, K., Liao, X. & Zhang, K. 2011 Simulations of fluid motion in ellipsoidal planetary cores driven by longitudinal libration. Phys. Earth Planet. Inter. 187, 391–403.CrossRefGoogle Scholar
Chan, K., Zhang, K. & Liao, X. 2010 An EBE finite element method for simulating nonlinear flows in rotating spheroidal cavities. Intl J. Numer. Meth. Fluids 63, 395–414.CrossRefGoogle Scholar
Dermott, S. F. 1979 Shapes and gravitational moments of satellites and asteroids. Icarus 37, 576–586.CrossRefGoogle Scholar
Gans, R. F. 1970 On the precession of a resonant cylinder. J. Fluid Mech. 41, 865–872.Google Scholar
Greenspan, H. P. 1964 On the transient motion of a contained rotating fluid. J. Fluid Mech. 21, 673–696.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hollerbach, R. & Kerswell, R. R. 1995 Oscillatory internal shear layers in rotating and precessing flows. J. Fluid Mech. 298, 327–339.CrossRefGoogle Scholar
Kobine, J. J. 1995 Inertial wave dynamics in a rotating and precessing cylinder. J. Fluid Mech. 303, 233–252.Google Scholar
Liao, X. & Zhang, K. 2012 On flow in weakly precessing cylinders: the general asymptotic solution. J. Fluid Mech. 709, 610–621.CrossRefGoogle Scholar
Manasseh, R. 1992 Breakdown regimes of inertia waves in a precessing cylinder. J. Fluid Mech. 243, 261–296.CrossRefGoogle Scholar
Margot, J. L., Peale, S. J., Jurgens, R. F., Slade, M. A. & Holin, I. V. 2007 Large longitude libration of mercury reveals a molten core. Science 316, 710–714.Google Scholar
Meunier, P., Eloy, C., Lagrange, R. & Nadal, 2008 A rotating fluid cylinder subject to weak precession. J. Fluid Mech. 599, 405–440.CrossRefGoogle Scholar
Noir, J., Calkins, M. A., Lasbleis, M., Cantwell, J. & Aurnou, J. M. 2010 Experimental study of libration-driven zonal flows in a straight cylinder. Phys. Earth Planet. Inter. 182, 98–106.Google Scholar
Noir, J., Cardin, P., Jault, D. & Masson, J. P. 2003 Experimental evidence of nonlinear resonance effects between retrograde precession and the tilt-over mode within a spheroid. Geophys. J. Intl 154, 407–416.Google Scholar
Noir, J., Cébron, D., Le Bars, M., Sauret, A. & Aurnou, J. M. 2012 Experimental study of libration-driven zonal flows in non-axisymmetric containers. Phys. Earth Planet. Inter. 204–205, 1–10.CrossRefGoogle Scholar
Noir, J., Hemmerlin, F., Wicht, J., Baca, S. M. & Aurnou, J. M. 2009 An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans. Phys. Earth Planet. Inter. 173, 141–152.CrossRefGoogle Scholar
Rieutord, M. 1991 Linear theory of rotating fluids using spherical harmonics part II, time-periodic flows. Geophys. Astrophys. Fluid Dyn. 59, 185–208.Google Scholar
Roberts, P. H. & Stewartson, K. 1965 On the motion of a liquid in a spheroidal cavity of a precessing rigid body: II. Math. Proc. Cambridge Phil. Soc. 61, 279–288.Google Scholar
Sauret, A., Cebron, D., Morize, C. & Le Bars, M. 2010 Experimental and numerical study of mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 662, 260–268.Google Scholar
Tilgner, A. 1999 Driven inertial oscillations in spherical shells. Phys. Rev. E 59, 1789–1794.Google Scholar
Tilgner, A. 2007 Rotational dynamics of the core. In Core Dynamics (ed. Schubert, G.), Treatise of Geophysics, vol. 8, pp. 207–243. Elsevier.Google Scholar
Wood, W. W. 1966 An oscillatory disturbance of rigidly rotating fluid. Proc. R. Soc. Lond. A 293, 181–212.Google Scholar
Zhang, K., Chan, K. & Liao, X. 2011 On fluid motion in librating ellipsoids with moderate equatorial eccentricity. J. Fluid Mech. 673, 468–479.CrossRefGoogle Scholar
Zhang, K., Chan, K. & Liao, X. 2012 Asymptotic theory of resonant flow in a spheroidal cavity driven by latitudinal libration. J. Fluid Mech. 692, 420–445.Google Scholar
Zhang, K., Earnshaw, P., Liao, X. & Busse, F. H. 2001 On inertial waves in a rotating fluid sphere. J. Fluid Mech. 437, 103–119.Google Scholar