Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T03:32:37.828Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-normality in combustion–acoustic interaction in diffusion flames: a critical revision

Published online by Cambridge University Press:  01 October 2013

Luca Magri ,
K. Balasubramanian ,
R. I. Sujith  and
M. P. Juniper
Luca Magri*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
K. Balasubramanian
Affiliation:
C. N. Yang Institute for Theoretical Physics, State University of New York, Stony Brook, NY 11794-3840, USA
R. I. Sujith
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Madras, Chennai 600036, Tamil Nadu, India
M. P. Juniper
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Perturbations in a non-normal system can grow transiently even if the system is linearly stable. If this transient growth is sufficiently large, it can trigger self-sustained oscillations from small initial disturbances. This has important practical consequences for combustion–acoustic oscillations, which are a persistent problem in rocket and aircraft engines. Balasubramanian & Sujith (J. Fluid Mech., vol. 594, 2008, pp. 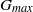29–57) modelled an infinite-rate chemistry diffusion flame in an acoustic duct and found that the transient growth in this system can amplify the initial energy by a factor, ${G}_{max} $, of the order of 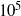$1{0}^{5} $ to 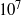$1{0}^{7} $. However, recent investigations by L. Magri and M. P. Juniper have brought to light certain errors in that paper. When the errors are corrected, 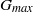${G}_{max} $ is found to be of the order of 1 to 10, revealing that non-normality is not as influential as it was thought to be.

JFM classification

Acoustics: Acoustics Reacting Flows: Combustion Reacting Flows: Flames
Type
Papers
Information
Journal of Fluid Mechanics , Volume 733 , 25 October 2013 , pp. 681 - 683
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balasubramanian, K. & Sujith, R. I. 2008 Non-normality and nonlinearity in combustion–acoustic interaction in diffusion flames. J. Fluid Mech. 594, 29–57.Google Scholar
Chu, B. T. 1965 On the energy transfer to small disturbances in fluid flow (Part I). Acta Mechanica 1 (3), 215–234.Google Scholar
Juniper, M. P. 2011 Triggering in the horizontal Rijke tube: non-normality, transient growth and bypass transition. J. Fluid Mech. 667, 272–308.Google Scholar
Illingworth, S. J., Waugh, I. C. & Juniper, M. P. 2013 Finding thermoacoustic limit cycles for a ducted Burke–Schumann flame. Proc. Combust. Inst. 34 (1), 911–920.Google Scholar
Trefethen, L. N. & Embree, M. 2005 Spectra and Pseudospectra. Princeton University Press.CrossRefGoogle Scholar