Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T13:20:46.519Z Has data issue: false hasContentIssue false
  • English
  • Français

A new method for isolating turbulent states in transitional stratified plane Couette flow

Published online by Cambridge University Press:  26 October 2016

J. R. Taylor ,
E. Deusebio ,
C. P. Caulfield  and
R. R. Kerswell
J. R. Taylor*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Willberforce Road, Cambridge CB3 0WA, UK
E. Deusebio
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Willberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Willberforce Road, Cambridge CB3 0WA, UK BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
R. R. Kerswell
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a new adaptive control strategy to isolate and stabilize turbulent states in transitional, stably stratified plane Couette flow in which the gravitational acceleration (non-dimensionalized as the bulk Richardson number 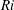$Ri$) is adjusted in time to maintain the turbulent kinetic energy (TKE) of the flow. We demonstrate that applying this method at various stages of decaying stratified turbulence halts the decay process and allows a succession of intermediate turbulent states of decreasing energy to be isolated and stabilized. Once the energy of the initial flow becomes small enough, we identify a single minimal turbulent spot, and lower-energy states decay to laminar flow. Interestingly, the turbulent states which emerge from this process have very similar time-averaged 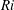$Ri$, but TKE levels different by an order of magnitude. The more energetic states consist of several turbulent spots, each qualitatively similar to the minimal turbulent spot. This suggests that the minimal turbulent spot may well be the lowest-energy turbulent state which forms a basic building block of stratified plane Couette flow. The fact that a minimal spot of turbulence can be stabilized, so that it neither decays nor grows, opens up exciting opportunities for further study of spatiotemporally intermittent stratified turbulence.

JFM classification

Geophysical and Geological Flows: Stratified flows Turbulent Flows: Stratified turbulence Instability: Transition to turbulence
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 808 , 10 December 2016 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alavyoon, F., Henningson, D. S. & Alfredsson, P. H. 1986 Turbulent spots in plane Poiseuille flow–flow visualization. Phys. Fluids 29 (4), 1328–1331.CrossRefGoogle Scholar
Barkley, D. & Tuckerman, L. S. 2005 Computational study of turbulent laminar patterns in Couette flow. Phys. Rev. Lett. 94 (1), 014502.Google Scholar
Bottin, S., Dauchot, O. & Daviaud, F. 1997 Intermittency in a locally forced plane Couette flow. Phys. Rev. Lett. 79 (22), 4377–4380.CrossRefGoogle Scholar
Brethouwer, G., Duguet, Y. & Schlatter, P. 2012 Turbulent–laminar coexistence in wall flows with Coriolis, buoyancy or Lorentz forces. J. Fluid Mech. 704, 137–172.Google Scholar
Carlson, D. R., Widnall, S. E. & Peeters, M. F. 1982 A flow-visualization study of transition in plane Poiseuille flow. J. Fluid Mech. 121, 487–505.Google Scholar
Clever, R. M., Busse, F. H. & Kelly, R. E. 1977 Instabilities of longitudinal convection rolls in Couette flow. Z. Angew. Math. Phys. 28 (5), 771–783.CrossRefGoogle Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21 (03), 385–425.Google Scholar
Dauchot, O. & Daviaud, F. 1995 Finite amplitude perturbation and spots growth mechanism in plane Couette flow. Phys. Fluids 7 (2), 335–343.Google Scholar
Deusebio, E., Brethouwer, G., Schlatter, P. & Lindborg, E. 2014 A numerical study of the unstratified and stratified Ekman layer. J. Fluid Mech. 755, 672–704.CrossRefGoogle Scholar
Deusebio, E., Caulfield, C. P. & Taylor, J. R. 2015 The intermittency boundary in stratified plane Couette flow. J. Fluid Mech. 781, 298–329.Google Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar-turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110 (3), 034502.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119–129.Google Scholar
Emmons, H. W. 1951 The laminar-turbulent transition in a boundary layer – Part I. J. Aero. Sci. 18 (7), 490–498.Google Scholar
Flores, O. & Riley, J. J. 2010 Analysis of turbulence collapse in stably stratified surface layers using direct numerical simulation. Boundary-Layer Meteorol. 129 (2), 241–259.Google Scholar
Fukudome, K., Iida, O. & Nagano, Y. 2009 The mechanism of energy transfer in turbulent Poiseuille flow at very low Reynolds number. In Proceedings of 6th International Symposium on Turbulence and Shear Flow Phenomena, pp. 471–476. Begel House.Google Scholar
García-Villalba, M. & del Álamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23 (4), 045104.CrossRefGoogle Scholar
Henningson, D., Spalart, P. & Kim, J. 1987 Numerical simulations of turbulent spots in plane Poiseuille and boundary-layer flow. Phys. Fluids 30 (10), 2914–2917.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70, 703–716.CrossRefGoogle Scholar
Kelly, R. E. 1977 The onset and development of Rayleigh–Bénard convection in shear flows: a review. Physico-Chem. Hydrodyn. 1, 65–79.Google Scholar
Klingmann, B. G. B. & Alfredsson, P. H. 1990 Turbulent spots in plane Poiseuille flow – measurements of the velocity field. Phys. Fluids A 2 (12), 2183–2195.Google Scholar
Lagha, M. & Manneville, P. 2007 Modeling of plane Couette flow. I: large scale flow around turbulent spots. Phys. Fluids 19 (9), 094105.Google Scholar
Lundbladh, A. & Johansson, A. V. 1991 Direct simulation of turbulent spots in plane Couette flow. J. Fluid Mech. 229, 499–516.Google Scholar
Mahrt, L. 1999 Stratified atmospheric boundary layers. Boundary-Layer Meteorol. 90 (3), 375–396.Google Scholar
Manneville, P. 2011 On the decay of turbulence in plane Couette flow. Fluid Dyn. Res. 43 (6), 065501.Google Scholar
Manneville, P. 2012 On the growth of laminar–turbulent patterns in plane Couette flow. Fluid Dyn. Res. 44 (3), 031412.Google Scholar
Philip, J. & Manneville, P. 2011 From temporal to spatiotemporal dynamics in transitional plane Couette flow. Phys. Rev. E 83 (3), 036308.Google Scholar
Prigent, A., Grégoire, G., Chaté, H., Dauchot, O. & van Saarloos, W. 2002 Large-scale finite-wavelength modulation within turbulent shear flows. Phys. Rev. Lett. 89 (1), 014501.Google Scholar
Schumacher, J. & Eckhardt, B. 2001 Evolution of turbulent spots in a parallel shear flow. Phys. Rev. E 63 (4), 046307.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in parallel shear flow. Phys. Rev. Lett. 96, 174101.Google Scholar
Tillmark, N. & Alfredsson, P. H. 1992 Experiments on transition in plane Couette flow. J. Fluid Mech. 235, 89–102.Google Scholar
Tsukahara, T., Seki, Y., Kawamura, H. & Tochio, D. 2005 DNS of turbulent channel flow at very low Reynolds numbers. In Proceedings of the 4th International Symposium on Turbulence and Shear Flow Phenomena, pp. 935–940. Begel House.Google Scholar
Van Atta, C. 1966 Exploratory measurements in spiral turbulence. J. Fluid Mech. 25 (03), 495–512.Google Scholar