Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T21:59:39.082Z Has data issue: false hasContentIssue false
  • English
  • Français

The linear spin-up of a stratified, rotating fluid in a square cylinder

Published online by Cambridge University Press:  14 September 2012

M. R. Foster  and
R. J. Munro
M. R. Foster
Affiliation:
Department of Mathematical Sciences, Rensselaer Polytechnic Institute, Troy, NY 12180, USA
R. J. Munro*
Affiliation:
Faculty of Engineering, University of Nottingham, Nottingham NG7 2RD, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Here we present experimental and theoretical results for how a stratified fluid, initially rotating as a solid body with constant angular velocity, 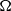$\Omega $, within a closed cylinder of square cross-section, is spun up when subject to a small, impulsive increase, 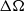$ \mrm{\Delta} \Omega $, in the cylinder’s rotation rate. The fluid’s adjustment to the new state of solid rotation can be characterized by: (a) an inviscid, horizontal starting flow which conserves the vorticity of the initial condition; (b) the eruption of Ekman layer fluid from the perimeter region of the cylinder’s base and lid; (c) horizontal-velocity Rayleigh layers that grow into the interior from the container’s sidewalls; and (d) the formation and decay of columnar vortices in the vertical corner regions. Asymptotic results describe the inviscid starting flow, and the subsequent interior spin-up that occurs due to the combined effects of Ekman suction through the base and lid Ekman layers, and the growth of the sidewall Rayleigh layers. Attention is focused on the flow development over the spin-up time scale 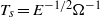${T}_{s} = {E}^{\ensuremath{-} 1/ 2} {\Omega }^{\ensuremath{-} 1} $, where $E$ is the Ekman number. (The spin-up process over the much longer diffusive time scale, 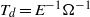${T}_{d} = {E}^{\ensuremath{-} 1} {\Omega }^{\ensuremath{-} 1} $, is not considered here.) Experiments were performed using particle imaging velocimetry (PIV) to measure horizontal velocity components at fixed heights within the flow interior and at regular stages during the spin-up period. The velocity data obtained are shown to be in excellent agreement with the asymptotic theory.

JFM classification

Boundary Layers: Boundary layer structure Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 712 , 10 December 2012 , pp. 7 - 40
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benton, E. R. & Clark, A. 1974 Spin-up. Annu. Rev. Fluid Mech. 6, 257–280.CrossRefGoogle Scholar
Duck, P. W. & Foster, M. R. 2001 Spin-up of homogeneous and stratified fluids. Annu. Rev. Fluid Mech. 33, 231–263.Google Scholar
Greenspan, H. P. & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.CrossRefGoogle Scholar
van Heijst, G. J. F. 1989 Spin-up phenomena in non-axisymmetric containers. J. Fluid Mech. 206, 171–191.Google Scholar
van Heijst, G. J. F., Davies, P. A. & Davis, R. G. 1990 Spin-up in a rectangular container. Phys. Fluids A 2, 150–159.Google Scholar
Jobe, C. E. & Burggraf, O. R. 1974 The numerical solution of asymptotic equations of trailing-edge flow. Proc. R. Soc. A 340, 91–111.Google Scholar
van de Konijnenberg, J. A. & van Heijst, G. J. F. 1997 Free-surface effects on spin-up in a rectangular tank. J. Fluid Mech. 334, 189–210.Google Scholar
Munro, R. J., Foster, M. R. & Davies, P. A. 2010 Instabilities in the spin-up of a rotating, stratified fluid. Phys. Fluids 22, 054108.Google Scholar
Oster, G. 1965 Density gradients. Sci. Am. 213 (2), 70–76.CrossRefGoogle Scholar
Sakurai, T. 1969 Spin down problem of rotating stratified fluid in thermally insulated circular cylinders. J. Fluid Mech. 37 (4), 689–699.Google Scholar
Spence, G. S. M., Foster, M. R. & Davies, P. A. 1992 The transient response of a contained rotating stratified fluid to impulsive surface forcing. J. Fluid Mech. 243, 33–50.Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.Google Scholar
Walin, G. 1969 Some aspects of time-dependent motion of a stratified rotating fluid. J. Fluid Mech. 36 (2), 289–307.CrossRefGoogle Scholar