Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sauret, Alban
Cébron, David
and
Le Bars, Michael
2013.
Spontaneous generation of inertial waves from boundary turbulence in a librating sphere.
Journal of Fluid Mechanics,
Vol. 728,
Issue. ,
Koch, S
Harlander, U
Egbers, C
and
Hollerbach, R
2013.
Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results.
Fluid Dynamics Research,
Vol. 45,
Issue. 3,
p.
035504.
Le Bars, Michael
2014.
Experimental and Computational Fluid Mechanics.
p.
83.
Cébron, D.
Vantieghem, S.
and
Herreman, W.
2014.
Libration-driven multipolar instabilities.
Journal of Fluid Mechanics,
Vol. 739,
Issue. ,
p.
502.
Sauret, Alban
Le Bars, Michael
and
Le Gal, Patrice
2014.
Tide‐driven shear instability in planetary liquid cores.
Geophysical Research Letters,
Vol. 41,
Issue. 17,
p.
6078.
Grannan, A. M.
Le Bars, M.
Cébron, D.
and
Aurnou, J. M.
2014.
Experimental study of global-scale turbulence in a librating ellipsoid.
Physics of Fluids,
Vol. 26,
Issue. 12,
Borcia, Ion Dan
Abouzar, Ghasemi V
and
Harlander, U
2014.
Inertial wave mode excitation in a rotating annulus with partially librating boundaries.
Fluid Dynamics Research,
Vol. 46,
Issue. 4,
p.
041423.
Klein, Marten
Seelig, Torsten
Kurgansky, Michael V.
Ghasemi V., Abouzar
Borcia, Ion Dan
Will, Andreas
Schaller, Eberhard
Egbers, Christoph
and
Harlander, Uwe
2014.
Inertial wave excitation and focusing in a liquid bounded by a frustum and a cylinder.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
255.
Favier, B.
Barker, A. J.
Baruteau, C.
and
Ogilvie, G. I.
2014.
Non-linear evolution of tidally forced inertial waves in rotating fluid bodies.
Monthly Notices of the Royal Astronomical Society,
Vol. 439,
Issue. 1,
p.
845.
Sauret, A
2015.
Mean zonal flow generated by azimuthal harmonic forcing in a rotating cylinder.
Fluid Dynamics Research,
Vol. 47,
Issue. 3,
p.
035506.
Le Dizès, Stéphane
2015.
Wave field and zonal flow of a librating disk.
Journal of Fluid Mechanics,
Vol. 782,
Issue. ,
p.
178.
Favier, B.
Grannan, A. M.
Le Bars, M.
and
Aurnou, J. M.
2015.
Generation and maintenance of bulk turbulence by libration-driven elliptical instability.
Physics of Fluids,
Vol. 27,
Issue. 6,
Le Bars, Michael
Cébron, David
and
Le Gal, Patrice
2015.
Flows Driven by Libration, Precession, and Tides.
Annual Review of Fluid Mechanics,
Vol. 47,
Issue. 1,
p.
163.
Seelig, T.
and
Harlander, U.
2015.
Can zonally symmetric inertial waves drive an oscillating zonal mean flow?.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 109,
Issue. 6,
p.
541.
Hoff, Michael
Harlander, U.
and
Egbers, C.
2016.
Experimental survey of linear and nonlinear inertial waves and wave instabilities in a spherical shell.
Journal of Fluid Mechanics,
Vol. 789,
Issue. ,
p.
589.
Kozlov, V.G.
Kozlov, N.V.
and
Subbotin, S.V.
2016.
Steady flows excited by circular oscillations of a free inner core in a rotating spherical cavity.
European Journal of Mechanics - B/Fluids,
Vol. 58,
Issue. ,
p.
85.
Kozlov, Victor G.
Kozlov, Nikolai V.
and
Subbotin, Stanislav V.
2017.
Steady flows in rotating spherical cavity excited by multi-frequency oscillations of free inner core.
Acta Astronautica,
Vol. 130,
Issue. ,
p.
43.
Kozlov, V. G.
and
Subbotin, S. V.
2017.
Librations induced zonal flow and differential rotation of free inner core in rotating spherical cavity.
Physics of Fluids,
Vol. 29,
Issue. 9,
Backus, George
and
Rieutord, Michel
2017.
Completeness of inertial modes of an incompressible inviscid fluid in a corotating ellipsoid.
Physical Review E,
Vol. 95,
Issue. 5,
Kong, Dejuan
Penkova, Anita
and
Sadhal, Satwindar Singh
2017.
Oscillatory and streaming flow between two spheres due to combined oscillations.
Journal of Fluid Mechanics,
Vol. 826,
Issue. ,
p.
335.
 $\varepsilon $ and small Ekman number
$\varepsilon $ and small Ekman number 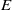 $E$. The mean flow is found to be at leading order an azimuthal flow that scales as the square of the libration amplitude and depends only on the cylindrical radius coordinate. The mean flow also exhibits a discontinuity across the cylinder tangent to the inner sphere. We show that this discontinuity can be smoothed through multi-scale Stewartson layers. The mean flow is also found to possess a weak axial flow that scales as
$E$. The mean flow is found to be at leading order an azimuthal flow that scales as the square of the libration amplitude and depends only on the cylindrical radius coordinate. The mean flow also exhibits a discontinuity across the cylinder tangent to the inner sphere. We show that this discontinuity can be smoothed through multi-scale Stewartson layers. The mean flow is also found to possess a weak axial flow that scales as 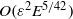 $O({\varepsilon }^{2} {E}^{5/ 42} )$ in the Stewartson layers. The analytical solution is compared to axisymmetric numerical simulations, and a good agreement is demonstrated.
$O({\varepsilon }^{2} {E}^{5/ 42} )$ in the Stewartson layers. The analytical solution is compared to axisymmetric numerical simulations, and a good agreement is demonstrated.