Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chaudhri, Anuj
Bell, John B.
Garcia, Alejandro L.
and
Donev, Aleksandar
2014.
Modeling multiphase flow using fluctuating hydrodynamics.
Physical Review E,
Vol. 90,
Issue. 3,
Meng, Jianping
and
Zhang, Yonghao
2014.
Diffuse reflection boundary condition for high-order lattice Boltzmann models with streaming–collision mechanism.
Journal of Computational Physics,
Vol. 258,
Issue. ,
p.
601.
Machado, Raúl
2014.
On the moment system and a flexible Prandtl number.
Modern Physics Letters B,
Vol. 28,
Issue. 06,
p.
1450048.
Ambruş, Victor Eugen
and
Sofonea, Victor
2014.
Implementation of diffuse-reflection boundary conditions using lattice Boltzmann models based on half-space Gauss-Laguerre quadratures.
Physical Review E,
Vol. 89,
Issue. 4,
Norouzi, Ali
and
Esfahani, Javad Abolfazli
2015.
Two relaxation time lattice Boltzmann equation for high Knudsen number flows using wall function approach.
Microfluidics and Nanofluidics,
Vol. 18,
Issue. 2,
p.
323.
Li, Jonathan
Liu, Haihu
Ioannou, Nikolaos
Zhang, Yonghao
and
Reese, Jason M.
2015.
Lattice Boltzmann Simulations of Thermocapillary Motion of Droplets in Microfluidic Channels.
Communications in Computational Physics,
Vol. 17,
Issue. 5,
p.
1113.
Meng, Jianping
Zhang, Yonghao
and
Reese, Jason M.
2015.
Numerical Simulation of Rarefied Gas Flows with Specified Heat Flux Boundary Conditions.
Communications in Computational Physics,
Vol. 17,
Issue. 5,
p.
1185.
Chen, Songze
Xu, Kun
and
Cai, Qingdong
2015.
A Comparison and Unification of Ellipsoidal Statistical and Shakhov BGK Models.
Advances in Applied Mathematics and Mechanics,
Vol. 7,
Issue. 2,
p.
245.
Li, Zhi-Hui
Peng, Ao-Ping
Zhang, Han-Xin
and
Yang, Jaw-Yen
2015.
Rarefied gas flow simulations using high-order gas-kinetic unified algorithms for Boltzmann model equations.
Progress in Aerospace Sciences,
Vol. 74,
Issue. ,
p.
81.
Yang, L.M.
Shu, C.
Wu, J.
and
Wang, Y.
2016.
Numerical simulation of flows from free molecular regime to continuum regime by a DVM with streaming and collision processes.
Journal of Computational Physics,
Vol. 306,
Issue. ,
p.
291.
Succi, Sauro
2016.
Lattice Boltzmann beyond Navier-Stokes: Where do we stand?.
Vol. 1786,
Issue. ,
p.
030001.
Di Staso, G.
Clercx, H. J. H.
Succi, S.
and
Toschi, F.
2016.
Lattice Boltzmann accelerated direct simulation Monte Carlo for dilute gas flow simulations.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 374,
Issue. 2080,
p.
20160226.
Ambruş, Victor E.
and
Sofonea, Victor
2016.
Lattice Boltzmann models based on half-range Gauss–Hermite quadratures.
Journal of Computational Physics,
Vol. 316,
Issue. ,
p.
760.
Norouzi, Ali
and
Esfahani, Javad Abolfazli
2016.
Capturing Non-equilibrium Effects of Micro/Nano Scale Gaseous Flow Using a Novel Lattice Boltzmann Model.
Journal of Statistical Physics,
Vol. 162,
Issue. 3,
p.
712.
Peng, Ao-Ping
Li, Zhi-Hui
Wu, Jun-Lin
and
Jiang, Xin-Yu
2016.
Implicit gas-kinetic unified algorithm based on multi-block docking grid for multi-body reentry flows covering all flow regimes.
Journal of Computational Physics,
Vol. 327,
Issue. ,
p.
919.
Di Staso, G.
Clercx, H.J.H.
Succi, S.
and
Toschi, F.
2016.
DSMC–LBM mapping scheme for rarefied and non-rarefied gas flows.
Journal of Computational Science,
Vol. 17,
Issue. ,
p.
357.
Ambruş, Victor E.
and
Sofonea, Victor
2016.
Application of mixed quadrature lattice Boltzmann models for the simulation of Poiseuille flow at non-negligible values of the Knudsen number.
Journal of Computational Science,
Vol. 17,
Issue. ,
p.
403.
Yasuoka, Haruka
Kaneda, Masayuki
and
Suga, Kazuhiko
2016.
Thermal lattice Boltzmann method for complex microflows.
Physical Review E,
Vol. 94,
Issue. 1,
Nassios, Jason
Yap, Ying Wan
and
Sader, John E.
2016.
Flow generated by oscillatory uniform heating of a rarefied gas in a channel.
Journal of Fluid Mechanics,
Vol. 800,
Issue. ,
p.
433.
Lai, Huilin
Xu, Aiguo
Zhang, Guangcai
Gan, Yanbiao
Ying, Yangjun
and
Succi, Sauro
2016.
Nonequilibrium thermohydrodynamic effects on the Rayleigh-Taylor instability in compressible flows.
Physical Review E,
Vol. 94,
Issue. 2,
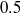 $0. 5$. On the other hand, highly non-equilibrium phenomena characterized by high Mach numbers, such as viscous heating and force-driven Poiseuille flow for large values of the driving force, are more difficult to capture quantitatively in the transition regime using discretizations chosen with computational efficiency in mind such as the one used here, although improved accuracy is observed as the number of discrete velocities is increased.
$0. 5$. On the other hand, highly non-equilibrium phenomena characterized by high Mach numbers, such as viscous heating and force-driven Poiseuille flow for large values of the driving force, are more difficult to capture quantitatively in the transition regime using discretizations chosen with computational efficiency in mind such as the one used here, although improved accuracy is observed as the number of discrete velocities is increased.