Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T22:31:44.286Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydrodynamic interactions among multiple circular cylinders in an inviscid flow

Published online by Cambridge University Press:  09 October 2012

R. Sun  and
C. O. Ng
R. Sun*
Affiliation:
Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai 200240, China
C. O. Ng
Affiliation:
Department of Mechanical Engineering, The University of Hong Kong, Pokfulam, Hong Kong, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Hydrodynamic interactions among multiple circular cylinders translating in an otherwise undisturbed inviscid fluid are theoretically investigated. A constructive method for solving a Neumann boundary-value problem in a domain outside $N$ circles (one kind of Hilbert boundary-value problem in the complex plane) is presented in the study to derive the velocity potential of the liquid. The method employs successive offset functions combined with a ‘generalized cyclic permutation’ in turn to satisfy the impenetrable boundary condition on each circle. The complex potential is therefore expressed as 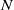$N$ isolated singularities in power series form and used to get instantaneous added masses of 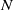$N$ submerged circular cylinders. Then, based on the Hamilton variational principle, a dynamical equation of motion in vector form is derived to predict nonlinear translations of the submerged bodies under fully hydrodynamic interactions. Also, the equivalence of the energy-based Lagrangian framework and a momentum-type one in the two-dimensional body–liquid system is proved. It implies that the pressure integration around a submerged body is holographic, which provides information about velocities and accelerations of all bodies. The numerical solutions indicate some typical dynamical behaviours of more than two circular cylinders which reveal that interesting nonlinear phenomena would appear in such a system with simple physical assumptions.

JFM classification

Mathematical Foundations: General fluid mechanics Mathematical Foundations: Hamiltonian theory Mathematical Foundations: Mathematical Foundations
Type
Papers
Information
Journal of Fluid Mechanics , Volume 712 , 10 December 2012 , pp. 505 - 530
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Burton, D. A., Gratus, J. & Tucker, R. W. 2004 Hydrodynamic forces on two moving discs. Theor. Appl. Mech. 31, 153–188.CrossRefGoogle Scholar
Crowdy, D. G. 2006 Analytical solutions for uniform potential flow past multiple cylinders. Eur. J. Mech. B Fluids 25 (4), 459–470.CrossRefGoogle Scholar
Crowdy, D. G. 2008 Explicit solution for the potential flow due to an assembly of stirrers in an inviscid fluid. J. Engng Maths 62 (4), 333–344.CrossRefGoogle Scholar
Crowdy, D. G. 2010 A new calculus for two-dimensional vortex dynamics. Theor. Comput. Fluid Dyn. 24, 9–24.CrossRefGoogle Scholar
Crowdy, D. G., Surana, A. & Yick, K.-Y. 2007 The irrotational motion generated by two planar stirrers in inviscid fluid. Phys. Fluids 19, 018103.CrossRefGoogle Scholar
Cummins, W. E. 1957 The force and moment on a body in a time-varying potential flow. J. Ship Res. 1, 1–7.CrossRefGoogle Scholar
Guo, Z. & Chwang, A. T. 1991 Oblique impact of two cylinders in a uniform flow. J. Ship Res. 35 (3), 219–229.CrossRefGoogle Scholar
Hicks, W. M. 1879 On the motion of two cylinders in a fluid. Q. J. Pure Appl. Maths 16, 113–140.Google Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Landweber, L. & Chwang, A. T. 1989 Generalization of Taylor’s added-mass formula for two bodies. J. Ship Res. 33 (1), 1–9.CrossRefGoogle Scholar
Landweber, L., Chwang, A. T. & Guo, Z. 1991 Interaction between two bodies translating in an inviscid fluid. J. Ship Res. 35 (1), 1–8.CrossRefGoogle Scholar
Landweber, L. & Miloh, T. 1980 Unsteady Lagally theorem for multipoles and deformable bodies. J. Fluid Mech. 96, 33–46.CrossRefGoogle Scholar
Landweber, L. & Yih, C. S. 1956 Forces, moments, and added masses for Rankine bodies. J. Fluid Mech. 1, 319–336.CrossRefGoogle Scholar
Milne-Thomson, L. M. 1960 Theoretical Hydrodynamics, 4th edn. Macmillan.Google Scholar
Miloh, T. & Landweber, L. 1981 Generalization of the Kelvin–Kirchhoff equations for the motion of a body through a fluid. Phys. Fluids 24 (1), 6–9.CrossRefGoogle Scholar
Nair, S. & Kanso, E. 2007 Hydrodynamically coupled rigid bodies. J. Fluid Mech. 592, 393–411.CrossRefGoogle Scholar
Sun, R. & Chwang, A. T. 2000 Hydrodynamic interaction between two cylinders with rotation. J. Phys. Soc Japan 70 (1), 91–102.CrossRefGoogle Scholar
Sun, R. & Chwang, A. T. 2006 Interaction of a floating elliptic cylinder with a vibrating circular cylinder. J. Hydrodyn. B 18 (4), 481–491.CrossRefGoogle Scholar
Taylor, G. I. 1928 The energy of a body moving in an infinite fluid, with an application to airships. Proc. R. Soc.Lond. A 120, 13–21.Google Scholar
Tchieu, A. A., Crowdy, D. G. & Leonard, A. 2010 Fluid–structure interaction of two bodies in an inviscid fluid. Phys. Fluids 22, 107101.CrossRefGoogle Scholar
Wang, Q. X. 2004 Interaction of two circular cylinders in inviscid fluid. Phys. Fluids 16, 4412–4425.CrossRefGoogle Scholar
Wang, Q. X. 2007 An analytical solution for two slender bodies of revolution translating in very close proximity. J. Fluid Mech. 582, 223–251.CrossRefGoogle Scholar
Wang, Q. X. 2005 Analysis of a slender body moving near a curved-ground. Phys. Fluids 17, 097102.CrossRefGoogle Scholar
Yamamoto, T. 1976 Hydrodynamic forces on multiple circular cylinders. ASCE J. Hydraul. Div. 102 (HY9), 1193–1210.CrossRefGoogle Scholar