Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T21:26:46.891Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics and invariants of the perceived velocity gradient tensor in homogeneous and isotropic turbulence

Published online by Cambridge University Press:  09 June 2020

Ping-Fan Yang ,
Alain Pumir Open the ORCID record for Alain Pumir [Opens in a new window]  and
Haitao Xu Open the ORCID record for Haitao Xu [Opens in a new window]
Ping-Fan Yang
Affiliation:
Center for Combustion Energy and Department of Energy and Power Engineering, Tsinghua University, 100084Beijing, PR China
Alain Pumir
Affiliation:
Laboratoire de Physique, Ecole Normale Supérieure de Lyon, CNRS, Université de Lyon, 69007Lyon, France Max Planck Institute for Dynamics and Self-Organization, Am Fassberg 17, 37077Göttingen, Germany
Haitao Xu*
Affiliation:
Center for Combustion Energy and School of Aerospace Engineering, Tsinghua University, 100084Beijing, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

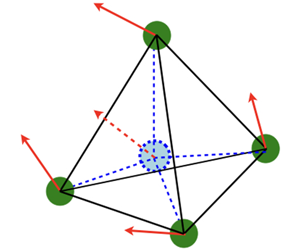
The perceived velocity gradient tensor (PVGT), constructed from four fluid tracers forming a tetrahedron, provides a natural way to study the structure of velocity fluctuations and its dependence on spatial scales. It generalizes and shares qualitatively many properties with the true velocity gradient tensor. Here, we establish the evolution equation for the PVGT, and, for homogeneous and isotropic incompressible turbulent flows, we analyse the dynamics of the PVGT in particular using its second- and third-order invariants. We show that, for PVGT based on regular tetrads with lateral size $R_{0}$, the second-order invariants can be expressed solely in terms of the usual second-order velocity structure functions, while the third-order invariants involve the usual third-order longitudinal velocity structure function and a less well known three-point velocity correlation function. For homogeneous and isotropic turbulence, exact relations between the second moments of strain and vorticity, as well as enstrophy production and the third moments of the strain, are derived. These generalized relations are valid for all ranges of $R_{0}$, and reduce to classical results for the velocity gradient tensor when $R_{0}$ is in the dissipative range. With the help of these relations, we quantify the importance of the various terms, such as vortex stretching, as a function of the scale $R_{0}$. Our analysis, which is supported by the results of direct numerical simulations of turbulent flows in the Reynolds-number range $100\leqslant R_{\unicode[STIX]{x1D706}}\leqslant 610$, allows us to demonstrate that strain prevails over vorticity when $R_{0}$ is in the inertial range.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 897 , 25 August 2020 , A9
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1, 497–504.CrossRefGoogle Scholar
Biferale, L., Boffetta, G., Celani, A., Devenish, B. J., Lanotte, A. & Toschi, F. 2005 Multiparticle dispersion in fully developed turbulence. Phys. Fluids 17, 111701.Google Scholar
Bodenschatz, E., Bewley, G. P., Nobach, H., Sinhuber, M. & Xu, H. 2014 Variable density turbulence tunnel facility. Rev. Sci. Instrum. 85, 093908.CrossRefGoogle ScholarPubMed
Borue, V. & Orszag, S. A. 1998 Local energy flux and subgrid-scale statistics in three-dimensional turbulence. J. Fluid Mech. 336, 1–31.CrossRefGoogle Scholar
Buaria, D., Pumir, A., Bodenschatz, E. & Yeung, P. K. 2019 Extreme velocity gradients in turbulent flows. New J. Phys. 21, 043004.CrossRefGoogle Scholar
Carbone, M. & Bragg, A. D. 2020 Is vortex stretching the main cause of the turbulent energy cascade? J. Fluid Mech. 883, R2.CrossRefGoogle Scholar
Chertkov, M., Pumir, A. & Shraiman, B. I. 1999 Lagrangian tetrad dynamics and the phenomenology of turbulence. Phys. Fluids 11, 2394–2410.CrossRefGoogle Scholar
Chevillard, L. & Meneveau, C. 2006 Lagrangian dynamics and statistical geometric structure of turbulence. Phys. Rev. Lett. 97, 174501.CrossRefGoogle ScholarPubMed
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.CrossRefGoogle Scholar
Davidson, P. A. 2015 Turbulence: An Introduction for Scientists and Engineers, 2nd edn. Oxford University Press.CrossRefGoogle Scholar
Devenish, B. J. 2013 Geometrical properties of turbulent dispersion. Phys. Rev. Lett. 110, 064504.CrossRefGoogle ScholarPubMed
Devenish, B. J. & Thomson, D. J. 2013 A Lagrangian stochastic model for tetrad dispersion. J. Turbul. 14, 107–120.CrossRefGoogle Scholar
Douady, S., Couder, Y. & Brachet, M. E. 1991 Direct observation of the intermittency of intense vorticity filaments in turbulence. Phys. Rev. Lett. 67, 983–986.CrossRefGoogle ScholarPubMed
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Hackl, J. F., Yeung, P. K. & Sawford, B. L. 2011 Multi-particle and tetrad statistics in numerical simulations of turbulent relative dispersion. Phys. Fluids 23 (6), 065103.CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y., Yosokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high resolution of numerically isotropic turbulence. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
Johnson, P. L. 2020 Energy transfer from large to small scales in turbulence by multi-scale nonlinear strain and vorticity interaction. Phys. Rev. Lett. 124, 104501.CrossRefGoogle Scholar
Johnson, P. L. & Meneveau, C. 2016 A closure for Lagrangian velocity gradient evolution in turbulence using recent-deformation mapping of initially Gaussian field. J. Fluid Mech. 804, 387–419.CrossRefGoogle Scholar
Johnson, P. L. & Meneveau, C. 2018 Predicting viscous-range velocity gradient dynamics in large-eddy simulations of turbulence. J. Fluid Mech. 837, 80–114.CrossRefGoogle Scholar
Jucha, J., Xu, H., Pumir, A. & Bodenschatz, E. 2014 Time-reversal-symmetry breaking in turbulence. Phys. Rev. Lett. 113, 054501.CrossRefGoogle ScholarPubMed
von Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164, 192–215.CrossRefGoogle Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. L. 2008 A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 9 (N31), 1–29.CrossRefGoogle Scholar
Lüthi, B., Ott, S., Berg, J. & Mann, J. 2007 Lagrangian multi-particle statistics. J. Turbul. 8 (N45), 1–17.CrossRefGoogle Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43, 219–245.CrossRefGoogle Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32.CrossRefGoogle Scholar
Meneveau, C. & Lund, T. S. 1994 On the Lagrangian nature of the turbulence energy cascade. Phys. Fluids 6, 2820–2825.CrossRefGoogle Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics. Cambridge University Press.Google Scholar
Mydlarski, L., Pumir, A., Shraiman, B. I., Siggia, E. D. & Warhaft, Z. 1998 Structures and multipoint correlators for turbulent advection: predictions and experiments. Phys. Rev. Lett. 81, 4373–4376.CrossRefGoogle Scholar
Naso, A. 2019 Multiscale analysis of the structure of homogeneous turbulence. Phys. Rev. Fluids 4, 024609.CrossRefGoogle Scholar
Naso, A. & Godeferd, F. S. 2012 Statistics of the perceived velocity gradient tensor in a rotating turbulent flow. New J. Phys. 14, 125002.CrossRefGoogle Scholar
Naso, A. & Pumir, A. 2005 Scale dependence of the coarse-grained velocity derivative tensor structure in turbulence. Phys. Rev. E 72, 056318.Google ScholarPubMed
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pumir, A., Bodenschatz, E. & Xu, H. 2013 Tetrahedron deformation and alignment of perceived vorticity and strain in a turbulent flow. Phys. Fluids 25, 035101.CrossRefGoogle Scholar
Pumir, A., Shraiman, B. I. & Chertkov, M. 2000 Geometry of Lagrangian dispersion in turbulence. Phys. Rev. Lett. 85 (25), 5324–5327.CrossRefGoogle ScholarPubMed
Sawford, B. L., Pope, S. B. & Yeung, P. K. 2013 Gaussian Lagrangian stochastic models for multi-particle dispersion. Phys. Fluids 25, 055101.CrossRefGoogle Scholar
Siggia, E. 1981 Numerical study of small-scale intermittency in three-dimensional turbulence. J. Fluid Mech. 107, 357–406.CrossRefGoogle Scholar
Tao, B., Katz, J. & Meneveau, C. 2002 Statistical geometry of subgrid-scale stresses determined from holographic particle image velocimetry measurements. J. Fluid Mech. 457, 35–78.CrossRefGoogle Scholar
Townsend, A. A. 1951 On the fine-scale structure of turbulence. Proc. R. Soc. Lond. A 208, 534–542.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence. Springer.CrossRefGoogle Scholar
Van der Bos, F., Tao, B., Meneveau, C. & Katz, J. 2002 Effects of small-scale turbulent motions on the filtered velocity gradient tensor as deduced from holographic particle image velocimetry measurements. Phys. Fluids 14, 2456–2474.CrossRefGoogle Scholar
Wu, J. Z., Fang, L., Shao, L. & Lu, L. P. 2018 Theories and applications of second-order correlation of longitudinal velocity increments at three points in isotropic turbulence. Phys. Lett. A 382, 1665–1671.CrossRefGoogle Scholar
Xu, H., Ouellette, N. T. & Bodenschatz, E. 2008 Evolution of geometric structures in intense turbulence. New J. Phys. 10, 013012.CrossRefGoogle Scholar
Xu, H., Pumir, A. & Bodenschatz, E. 2011 The pirouette effect in turbulent flows. Nat. Phys. 7, 709–712.CrossRefGoogle Scholar
Xu, H., Pumir, A. & Bodenschatz, E. 2016 Lagrangian view of time irreversibility of fluid turbulence. Sci. China-Phys. Mech. Astron. 59 (1), 614702.CrossRefGoogle Scholar
Yao, S. Y., Fang, L., Lv, J. M., Wu, J. Z. & Lu, L. P. 2014 Multiscale three-point velocity increment correlation in turbulent flows. Phys. Lett. A 378, 885–891.CrossRefGoogle Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2012 Dissipation, enstrophy and pressure statistics in turbulence simulations at high Reynolds numbers. J. Fluid Mech. 700, 5–15.CrossRefGoogle Scholar