Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T23:28:13.090Z Has data issue: false hasContentIssue false
  • English
  • Français

Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1. Energy spectra

Published online by Cambridge University Press:  12 November 2019

Woutijn J. Baars Open the ORCID record for Woutijn J. Baars [Opens in a new window]  and
Ivan Marusic Open the ORCID record for Ivan Marusic [Opens in a new window]
Woutijn J. Baars*
Affiliation:
Department of Engineering, Aarhus University, 8000 Aarhus C, Denmark
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

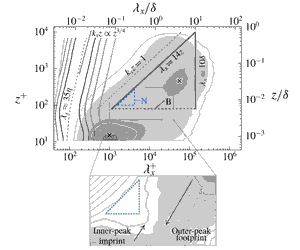
In wall-bounded turbulence, a multitude of coexisting turbulence structures form the streamwise velocity energy spectrum from the viscosity- to the inertia-dominated range of scales. Definite scaling-trends for streamwise spectra have remained empirically elusive, although a prominent school of thought stems from the works of Perry & Abell (J. Fluid Mech., vol. 79, 1977, pp. 785–799) and Perry et al. (J. Fluid Mech., vol. 165, 1986, pp. 163–199), which were greatly inspired by the attached-eddy hypothesis of Townsend (The Structure of Turbulent Shear Flow, Cambridge University Press, 1976). In this paper, we re-examine the turbulence kinetic energy of the streamwise velocity component in the context of the spectral decompositions of Perry and co-workers. Two universal spectral filters are derived via spectral coherence analysis of two-point velocity signals, spanning a Reynolds-number range $Re_{\unicode[STIX]{x1D70F}}\sim O(10^{3})$ to $O(10^{6})$ and form the basis for our decomposition of the logarithmic-region turbulence into stochastically wall-detached and wall-attached portions of energy. The latter is composed of scales larger than a streamwise/wall-normal ratio of $\unicode[STIX]{x1D706}_{x}/z\approx 14$. If the decomposition is accepted, a $k_{x}^{-1}$ scaling region can only appear for $Re_{\unicode[STIX]{x1D70F}}\gtrsim 80\,000$, at a wall-normal position of $z^{+}=100$. Following Perry and co-workers, it is hypothesized that spectral contributions from turbulence structures other than attached eddies obscure a $k_{x}^{-1}$ scaling. When accepting the idea of different spectral contributions it is furthermore shown that a broad outer-spectral peak is present even at low $Re_{\unicode[STIX]{x1D70F}}$.

JFM classification

Turbulent Flows: Turbulent boundary layers Boundary Layers: Boundary layer structure
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 882 , 10 January 2020 , A25
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 1979 Conditional eddies in isotropic turbulence. Phys. Fluids 22 (11), 2065–2070.Google Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Adrian, R. J., Moin, P. & Moser, R. D. 1987 Stochastic estimation of conditional eddies in turbulent channel flow. In Proc. of the Summer Program 1987, Center for Turbulence Research, pp. 7–19. Stanford University, CTR-S87.Google Scholar
Agostini, L. & Leschziner, M. 2017 Spectral analysis of near-wall turbulence in channel flow at Re 𝜏 = 4200 with emphasis on the attached-eddy hypothesis. Phys. Rev. Fluids 2, 014603.Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.Google Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2016a Spectral stochastic estimation of high-Reynolds-number wall-bounded turbulence for a refined inner–outer interaction model. Phys. Rev. Fluids 1, 054406.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017a Reynolds number trend of hierarchies and scale interactions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 375, 20160077.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017b Self-similarity of wall-attached turbulence in boundary layers. J. Fluid Mech. 823, R2.Google Scholar
Baars, W. J. & Marusic, I. 2020 Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 2. Integrated energy and A 1 . J. Fluid Mech. 882, A26.Google Scholar
Baars, W. J., Squire, D. T., Talluru, K. M., Abbassi, M. R., Hutchins, N. & Marusic, I. 2016b Wall-drag measurements of smooth- and rough-wall turbulent boundary layers using a floating element. Exp. Fluids 57 (90), 1–16.Google Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29, 020712.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google Scholar
Bendat, J. S. & Piersol, A. G. 1986 Random Data Analysis and Measurement Procedures. Wiley.Google Scholar
Beresh, S. J., Henfling, J. F., Spillers, R. W. & Spitzer, S. M. 2018 ‘Postage-stamp PIV’: small velocity fields at 400 kHz for turbulence spectra measurements. Meas. Sci. Technol. 29, 034011.Google Scholar
Blackwelder, R. F. & Kovasznay, L. S. G. 1972 Time scales and correlations in a turbulent boundary layer. Phys. Fluids 15 (9), 1545–1554.Google Scholar
Bonnet, J. P., Delville, J., Glauser, M. N., Antonia, R. A., Bisset, D. K., Cole, D. R., Fiedler, H. E., Garem, J. H., Hilberg, D., Jeong, J. et al. 1998 Collaborative testing of eddy structure identification methods in free turbulent shear flows. Exp. Fluids 25 (3), 197–225.Google Scholar
Brown, G. L. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20 (10), S243–S252.Google Scholar
Bullock, K. J., Cooper, R. E. & Abernathy, F. H. 1978 Structural similarity in radial correlations and spectra of longitudinal velocity fluctuations in pipe flow. J. Fluid Mech. 88, 585–608.Google Scholar
Calaf, M., Hultmark, M., Oldroyd, H. J., Simeonov, V. & Parlange, M. B. 2013 Coherent structures and the k -1 spectral behaviour. Phys. Fluids 25, 125107.Google Scholar
Chandran, D., Baidya, R., Monty, J. P. & Marusic, I. 2017 Two-dimensional energy spectra in a high Reynolds number turbulent boundary layer. J. Fluid Mech. 826, R1.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Cole, D. R. & Glauser, M. N. 1998 Applications of stochastic estimation in the axisymmetric sudden expansion. Phys. Fluids 10 (11), 2941–2949.Google Scholar
Davidson, P. A. & Krogstad, P.-Å. 2008 On the deficiency of even-order structure functions as inertial-range diagnostics. J. Fluid Mech. 602, 287–302.Google Scholar
Davidson, P. A. & Krogstad, P.-Å. 2009 A simple model for the streamwise fluctuations in the log-law region of a boundary layer. Phys. Fluids 21, 055105.Google Scholar
Davidson, P. A., Nickels, T. B. & Krogstad, P.-Å. 2006 The logarithmic structure function law in wall-layer turbulence. J. Fluid Mech. 550, 51–60.Google Scholar
Ewing, D. & Citriniti, J. 1999 Examination of a LSE/POD complementary technique using single and multi-time information in the axisymmetric shear layer. In Proceedings of the IUTAM Symposium on Simulation and Identification of Organized Structures in Flows (ed. Sorensen, J. N., Hopfinger, E. J. & Aubry, N.), p. 384. IUTAM.Google Scholar
Favre, A. J., Gaviglio, J. J. & Dumas, R. 1967 Structure of velocity space–time correlations in a boundary layer. Phys. Fluids 10 (9), S138–S145.Google Scholar
Gamard, S. & George, W. K. 2000 Reynolds number dependence of energy spectra in the overlap region of isotropic turbulence. Flow Turb. Combust. 63, 443–477.Google Scholar
Ganapathisubramani, B. 2018 Law-of-the-wall for streamwise energy spectra in high-Reynolds-number turbulent boundary layers. Phys. Rev. Fluids 3, 104607.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
de Giovanetti, M., Sung, H. J. & Hwang, Y. 2017 Streak instability in turbulent channel flow: the seeding mechanism of large-scale motions. J. Fluid Mech. 832, 483–513.Google Scholar
Guezennec, Y. G. 1989 Stochastic estimation of coherent structures in turbulent boundary layers. Phys. Fluids A 1 (6), 1054–1060.Google Scholar
Head, M. R. & Bandyopadhyay, P. R. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–337.Google Scholar
Heuer, W. D. C. & Marusic, I. 2005 Turbulence wall-shear stress sensor for the atmospheric surface layer. Meas. Sci. Technol. 16, 1644–1649.Google Scholar
Högström, U., Hunt, J. C. R. & Smedman, A.-S. 2002 Theory and measurements for turbulence spectra and variances in the atmospheric neutral surface layer. Boundary-layer Meteorol. 103, 101–124.Google Scholar
Hunt, J. C. R. & Carlotti, P. 2001 Statistical structure at the wall of the high Reynolds number turbulent boundary layer. Flow Turb. Combust. 66, 453–475.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.Google Scholar
Hwang, Y. & Cossu, C. 2010a Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.Google Scholar
Hwang, Y. & Cossu, C. 2010b Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Jones, M. B., Marusic, I. & Perry, A. E. 2001 Evolution and structure of sink-flow turbulent boundary layers. J. Fluid Mech. 428, 1–27.Google Scholar
de Kat, R. & Ganapathisubramani, B. 2015 Frequency–wavenumber mapping in turbulent shear flows. J. Fluid Mech. 783, 166–190.Google Scholar
Katul, G. G., Porporato, A. & Nikora, V. 2012 Existence of k -1 power-law scaling in the equilibrium regions of wall-bounded turbulence explained by Heisenberg’s eddy viscosity. Phys. Rev. E 86, 066311.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Rundstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Krug, D., Baars, W. J., Hutchins, N. & Marusic, I. 2019 Vertical coherence of turbulence in the atmospheric surface layer: connecting the hypotheses of Townsend and Davenport. Boundary-layer Meteorol. 172 (2), 199–214.Google Scholar
Kulandaivelu, V.2011 Evolution and structure of zero pressure gradient turbulent boundary layer. PhD thesis, The University of Melbourne, Melbourne, Australia.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5 (6), 407–417.Google Scholar
Long, R. R. & Chen, T. C. 1981 Experimental evidence for the existence of the mesolayer in turbulent systems. J. Fluid Mech. 105, 19–59.Google Scholar
Marusic, I., Baars, W. J. & Hutchins, N. 2017 Scaling of the streamwise turbulence intensity in the context of inner–outer interactions in wall-turbulence. Phys. Rev. Fluids 2, 100502.Google Scholar
Marusic, I., Chauhan, K. A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.Google Scholar
Marusic, I. & Heuer, W. D. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99, 114504.Google Scholar
Marusic, I. & Monty, J. P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Marusic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Morrison, J. F., Jiang, W., McKeon, B. J. & Smits, A. J. 2002 Reynolds number dependence of streamwise velocity spectra in turbulent pipe flow. Phys. Rev. Lett. 88 (21), 214501.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A. 2007 Approach to an asymptotic state for zero pressure gradient turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 365, 755–770.Google Scholar
Naguib, A. M., Wark, C. E. & Juckenhöfel, O. 2001 Stochastic estimation and flow sources associated with surface pressure events in a turbulent boundary layer. Phys. Fluids 13 (9), 2611–2626.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k 1 -1 law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.Google Scholar
Nikora, V. 1999 Origin of the ‘ - 1’ spectral law in wall-bounded turbulence. Phys. Rev. Lett. 83, 734–736.Google Scholar
Perry, A. E. & Abell, C. J. 1975 Scaling laws for pipe-flow turbulence. J. Fluid Mech. 67, 257–271.Google Scholar
Perry, A. E. & Abell, C. J. 1977 Asymptotic similarity of turbulence structures in smooth- and rough-walled pipes. J. Fluid Mech. 79, 785–799.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Renard, N. & Deck, S. 2015 On the scale-dependent turbulent convection velocity in a spatially developing flat plate turbulent boundary layer at Reynolds number Re 𝜃 = 13 000. J. Fluid Mech. 775, 105–148.Google Scholar
Robinson, S. K. 1991 Coherent motions in turbulent boundary layers. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Samie, M.2017 Sub-miniature hot-wire anemometry for high Reynolds number turbulent flows. PhD thesis, The University of Melbourne, Melbourne, Australia.Google Scholar
Samie, M., Marusic, I., Hutchins, N., Fu, M. K., Fan, Y., Hultmark, M. & Smits, A. J. 2018 Fully resolved measurements of turbulent boundary layer flows up to Re 𝜏 = 20 000. J. Fluid Mech. 851, 391–415.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25, 105102.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.Google Scholar
Srinath, S., Vassilicos, J. C., Cuvier, C., Laval, J.-P., Stanislas, M. & Foucaut, J.-M. 2018 Attached flow structure and streamwise energy spectra in a turbulent boundary layer. Phys. Rev. E 97, 053103.Google Scholar
Talluru, K. M., Kulandaivelu, V., Hutchins, N. & Marusic, I. 2014 A calibration technique to correct sensor drift issues in hot-wire anemometry. Meas. Sci. Technol. 25, 105304.Google Scholar
Tchen, C. M. 1953 On the spectrum of energy in turbulent shear flow. J. Res. Natl. Bur. Stand. 50 (1), 51–62.Google Scholar
Tinney, C. E., Coiffet, F., Delville, J., Glauser, M. N., Jordan, P. & Hall, A. M. 2006 On spectral linear stochastic estimation. Exp. Fluids 41 (5), 763–775.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015a Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.Google Scholar
Vallikivi, M., Hultmark, M. & Smits, A. J. 2015b Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.Google Scholar
Vassilicos, J. C., Laval, J.-P., Foucaut, J.-M. & Stanislas, M. 2015 The streamwise turbulence intensity in the intermediate layer of turbulent pipe flow. J. Fluid Mech. 774, 324–341.Google Scholar
Wark, C. E. & Nagib, H. M. 1991 Experimental investigation of coherent structures in turbulent boundary layers. J. Fluid Mech. 230, 183–208.Google Scholar
Woodcock, J. D. & Marusic, I. 2015 The statistical behavior of attached eddies. Phys. Fluids 27, 015104.Google Scholar
Wosnik, M., Castillo, L. & George, W. K. 2000 A theory for turbulent pipe and channel flows. J. Fluid Mech. 421, 115–145.Google Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.Google Scholar