Published online by Cambridge University Press: 08 February 2013
Spanwise-periodic roughness designed to excite selected wavelengths of stationary cross-flow modes was investigated in a three-dimensional boundary layer at Mach 3.5. The test model was a sharp-tipped 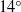 $1{4}^{\circ } $ right-circular cone. The model and integrated sensor traversing system were placed in the Mach 3.5 supersonic low disturbance tunnel (SLDT) equipped with an axisymmetric ‘quiet design’ nozzle at NASA Langley Research Center. The model was oriented at a
$1{4}^{\circ } $ right-circular cone. The model and integrated sensor traversing system were placed in the Mach 3.5 supersonic low disturbance tunnel (SLDT) equipped with an axisymmetric ‘quiet design’ nozzle at NASA Langley Research Center. The model was oriented at a 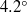 $4. {2}^{\circ } $ angle of attack to produce a mean cross-flow velocity component in the boundary layer over the cone. The research examined both passive and active surface roughness. The passive roughness consisted of indentations (dimples) that were evenly spaced around the cone at an axial location that was just upstream of the first linear stability neutral growth branch for cross-flow modes. The active roughness consisted of an azimuthal array of micrometre-sized plasma actuators that were designed to produce the effect of passive surface bumps. Two azimuthal mode numbers of the passive and active patterned roughness were examined. One had an azimuthal mode number that was in the band of initially amplified stationary cross-flow modes. This was intended to represent a controlled baseline condition. The other azimuthal mode number was designed to suppress the growth of the initially amplified stationary cross-flow modes and thereby increase the transition Reynolds number. The results showed that the stationary cross-flow modes were receptive to both the passive and active patterned roughness. Only the passive roughness was investigated at a unit Reynolds number where transition would occur on the cone. Transition front measurements using the Preston tube approach indicated that the transition Reynolds number had increased by 35 % with the subcritical wavenumber roughness compared with the baseline smooth tip cone, and by 40 % compared with the critical wavenumber roughness. Based on the similarities in the response of the stationary cross-flow modes with the active roughness, we expect it would produce a similar transition delay.
$4. {2}^{\circ } $ angle of attack to produce a mean cross-flow velocity component in the boundary layer over the cone. The research examined both passive and active surface roughness. The passive roughness consisted of indentations (dimples) that were evenly spaced around the cone at an axial location that was just upstream of the first linear stability neutral growth branch for cross-flow modes. The active roughness consisted of an azimuthal array of micrometre-sized plasma actuators that were designed to produce the effect of passive surface bumps. Two azimuthal mode numbers of the passive and active patterned roughness were examined. One had an azimuthal mode number that was in the band of initially amplified stationary cross-flow modes. This was intended to represent a controlled baseline condition. The other azimuthal mode number was designed to suppress the growth of the initially amplified stationary cross-flow modes and thereby increase the transition Reynolds number. The results showed that the stationary cross-flow modes were receptive to both the passive and active patterned roughness. Only the passive roughness was investigated at a unit Reynolds number where transition would occur on the cone. Transition front measurements using the Preston tube approach indicated that the transition Reynolds number had increased by 35 % with the subcritical wavenumber roughness compared with the baseline smooth tip cone, and by 40 % compared with the critical wavenumber roughness. Based on the similarities in the response of the stationary cross-flow modes with the active roughness, we expect it would produce a similar transition delay.