Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T18:21:26.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Skin-friction generation by attached eddies in turbulent channel flow

Published online by Cambridge University Press:  03 November 2016

Matteo de Giovanetti ,
Yongyun Hwang  and
Haecheon Choi
Matteo de Giovanetti
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK
Yongyun Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK
Haecheon Choi
Affiliation:
Department of Mechanical and Aerospace Engineering, Seoul National University, Seoul 08826, South Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Despite a growing body of recent evidence on the hierarchical organization of the self-similar energy-containing motions in the form of Townsend’s attached eddies in wall-bounded turbulent flows, their role in turbulent skin-friction generation is currently not well understood. In this paper, the contribution of each of these self-similar energy-containing motions to turbulent skin friction is explored up to 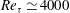$Re_{\unicode[STIX]{x1D70F}}\simeq 4000$. Three different approaches are employed to quantify the skin-friction generation by the motions, the spanwise length scale of which is smaller than a given cutoff wavelength: (i) FIK (Fukagata, Iwamoto, Kasagi) identity in combination with the spanwise wavenumber spectra of the Reynolds shear stress; (ii) confinement of the spanwise computational domain; (iii) artificial damping of the motions to be examined. The near-wall motions are found to continuously reduce their role in skin-friction generation on increasing the Reynolds number, consistent with the previous finding at low Reynolds numbers. The largest structures given in the form of very-large-scale and large-scale motions are also found to be of limited importance: due to a non-trivial scale interaction process, their complete removal yields only a 5–8 % skin-friction reduction at all of the Reynolds numbers considered, although they are found to be responsible for 20–30 % of total skin friction at $Re_{\unicode[STIX]{x1D70F}}\simeq 2000$. Application of all the three approaches consistently reveals that the largest amount of skin friction is generated by the self-similar motions populating the logarithmic region. It is further shown that the contribution of these motions to turbulent skin friction gradually increases with the Reynolds number, and that these coherent structures are eventually responsible for most of turbulent skin-friction generation at sufficiently high Reynolds numbers.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 808 , 10 December 2016 , pp. 511 - 538
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. Trans. ASME J. Fluids Engng 126 (5), 835.CrossRefGoogle Scholar
Agostini, L. & Leschziner, M. 2016 Predicting the response of small-scale near-wall turbulence to large-scale outer motions. Phys. Fluids 28 (1), 015107.Google Scholar
Agostini, L., Touber, E. & Leschziner, M. A. 2014 Spanwise oscillatory wall motion in channel flow: drag-reduction mechanisms inferred from DNS-predicted phase-wise property variations at Re 𝜏 = 1000. J. Fluid Mech. 743, 606–635.Google Scholar
del Alamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), 41–44.Google Scholar
del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Baars, W. J., Talluru, K. M., Hutchins, N. & Marusic, I. 2015 Wavelet analysis of wall turbulence to study large-scale modulation of small scales. Exp. Fluids 56 (10), 1–15.CrossRefGoogle Scholar
Bengana, Y. & Hwang, Y. 2015 Minimal dynamics of self-sustaining attached eddies in a turbulent channel. In International Symposium on Turbulent Shear Flow, Melbourne, 4A-2.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.CrossRefGoogle Scholar
Blesbois, O., Chernyshenko, S. I., Touber, E. & Leschziner, M. A. 2013 Pattern prediction by linear analysis of turbulent flow with drag reduction by wall oscillation. J. Fluid Mech. 724, 607–641.Google Scholar
Bushnell, D. M. 2002 Aircraft drag reduction – a review. J. Aerosp. Engng 217, 1–18.Google Scholar
Chang, Y., Collis, S. S. & Ramakrishnan, S. 2002 Viscous effects in control of near-wall turbulence. Phys. Fluids 14 (11), 4069–4080.Google Scholar
Chernyshenko, S. I. & Baig, M. F. 2005 The mechanism of streak formation in near-wall turbulence. J. Fluid Mech. 544, 99–131.Google Scholar
Chernyshenko, S. I., Marusic, I. & Mathis, R.2012 Quasi-steady description of modulation effects in wall turbulence. arXiv:1203.3714v1 [physics.flu-dyn], p. 16.Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.Google Scholar
Choi, H., Moin, P. & Kim, J. 1994 Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 262, 75–110.Google Scholar
Cimarelli, A., De Angelis, E., Jiménez, J. & Casciola, C. M. 2016 Cascades and wall-normal fluxes in turbulent channel flows. J. Fluid Mech. 796, 417–436.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.CrossRefGoogle Scholar
Dean, R. B. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. Trans. ASME J. Fluids Engng 100, 215–223.Google Scholar
Deck, S., Renard, N., Laraufie, R. & Weiss, P.-É. 2014 Large-scale contribution to mean wall shear stress in high-Reynolds-number flat-plate boundary layers up to Re 𝜃 = 13 650. J. Fluid Mech. 743, 202–248.Google Scholar
Dukowicz, J. K. & Dvinsky, A. S. 1992 Approximate factorization as a high order splitting for the implicit incompressible flow equations. J. Comput. Phys. 102 (2), 336–347.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 1–4.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), 13–17.Google Scholar
García-mayoral, R. & Jiménez, J. 2011 Drag reduction by riblets. Phil. Trans. R. Soc. Lond. A 369 (1940), 1412–1427.Google Scholar
Gatti, D. & Quadrio, M. 2013 Performance losses of drag-reducing spanwise forcing at moderate values of the Reynolds number. Phys. Fluids 25 (12), 125109.CrossRefGoogle Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3, 1760–1765.Google Scholar
Gullbrand, J. 2000 An evaluation of a conservative fourth order DNS code in turbulent channel flow. In Cent. Turbul. Res. Annu. Briefs, pp. 211–218.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 1–4.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google ScholarPubMed
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.Google Scholar
Hwang, Y. & Bengana, Y. 2016 Self-sustaining process of minimal attached eddies in turbulent channel flow. J. Fluid Mech. 795, 708–738.Google Scholar
Hwang, Y. & Cossu, C. 2010a Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Hwang, Y. & Cossu, C. 2010b Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 1–10.Google Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23 (6), 061702.Google Scholar
Jeong, J. & Hussain, F. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.CrossRefGoogle Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 231–240.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Jung, W., Mangiavacchi, N. & Akhavan, R. 1992 Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations. Phys. Fluids 4 (8), 1605–1607.CrossRefGoogle Scholar
Kasagi, N., Suzuki, Y. & Fukagata, K. 2009 Microelectromechanical systems-based feedback control of turbulence for skin friction reduction. Annu. Rev. Fluid Mech. 41 (1), 231–251.Google Scholar
Keirsbulck, L., Labraga, L. & Gad-El-Hak, M. 2012 Statistical properties of wall shear stress fluctuations in turbulent channel flows. Intl J. Heat Fluid Flow 37, 1–8.Google Scholar
Kim, J. & Lim, J. 2000 A linear process in wall-bounded turbulent shear flows. Phys. Fluids 12 (8), 1885–1888.Google Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Rundstatler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kornilov, V. I. 2015 Current state and prospects of researches on the control of turbulent boundary layer by air blowing. Prog. Aerosp. Sci. 76, 1–23.Google Scholar
Kovasznay, L. S. G. 1970 The turbulent boundary layer. Annu. Rev. Fluid Mech. 2 (1), 95–112.Google Scholar
Kravchenko, A. G., Choi, H. & Moin, P. 1993 On the relation of near-wall streamwise vortices to wall skin friction in turbulent boundary layers. Phys. Fluids A 5 (12), 3307–3309.Google Scholar
Kravchenko, A. G. & Moin, P. 1997 On the effect of numerical errors in large eddy simulations of turbulent flows. J. Comput. Phys. 131, 310–322.CrossRefGoogle Scholar
Landahl, M. T. 1990 On sublayer streaks. J. Fluid Mech. 212, 593–614.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Lim, J. & Kim, J. 2004 A singular value analysis of boundary layer control. Phys. Fluids 16 (6), 1980–1988.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.Google Scholar
Luhar, M., Sharma, A. S. & Mckeon, B. J. 2014 On the structure and origin of pressure fluctuations in wall turbulence: predictions based on the resolvent analysis. J. Fluid Mech. 751, 38–70.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.CrossRefGoogle Scholar
Moarref, R. & Jovanović, M. R. 2012 Model-based design of transverse wall oscillations for turbulent drag reduction. J. Fluid Mech. 707, 205–240.Google Scholar
Orlandi, P. & Jimenez, J. 1994 On the generation of turbulent wall friction. Phys. Fluids 6 (2), 634.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in turbulent Couette and Poiseulle flows. C. R. Mec. 339 (1), 1–5.Google Scholar
Park, N., Lee, S., Lee, J. & Choi, H. 2006 A dynamic subgrid-scale eddy viscosity model with a global model coefficient. Phys. Fluids 18, 125109.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21 (1), 1–6.Google Scholar
Quadrio, M. 2011 Drag reduction in turbulent boundary layers by in-plane wall motion. Phil. Trans. R. Soc. Lond. A 369 (1940), 1428–1442.Google Scholar
Renard, N. & Deck, S. 2016 A theoretical decomposition of mean skin friction generation into physical phenomena across the boundary layer. J. Fluid Mech. 790, 339–367.Google Scholar
Sarghini, F., Piomelli, U. & Balaras, E. 1999 Scale-similar models for large-eddy simulations. Phys. Fluids 11 (6), 1596–1607.Google Scholar
Schlatter, P., Örlü, R., Li, Q., Brethouwer, G., Fransson, J. H. M., Johansson, A. V., Alfredsson, P. H. & Henningson, D. S. 2009 Turbulent boundary layers up to Re 𝜃 = 2500 studied through simulation and experiment. Phys. Fluids 21 (5), 051702.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Schultz, M. P. & Flack, K. A. 2013 Reynolds-number scaling of turbulent channel flow. Phys. Fluids 25 (2), 1–13.Google Scholar
de Silva, C. M., Gnanamanickam, E. P., Atkinson, C., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I. 2014 High spatial range velocity measurements in a high Reynolds number turbulent boundary layer. Phys. Fluids 26 (2), 025117.Google Scholar
Spalart, P. R. & Mclean, J. D. 2011 Drag reduction: enticing turbulence, and then an industry. Phil. Trans. R. Soc. Lond. A 369 (1940), 1556–1569.Google Scholar
Squire, L. C. & Savill, A. M. 1989 Drag measurements on planar riblet surfaces at high subsonic speeds. Appl. Sci. Res. 46 (3), 229–243.Google Scholar
Stadsted, O. & Moin, P. 1991 On the mechanics of 3-D turbulent boundary layer. In Proc. Eighth Symp. Turbul. Shear Flows, Munich.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141.Google Scholar
Touber, E. & Leschziner, M. A. 2012 Near-wall streak modification by spanwise oscillatory wall motion and drag-reduction mechanisms. J. Fluid Mech. 693, 150–200.Google Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 12, 97–120.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 1st edn. Cambridge University Press.Google Scholar
Viswanath, P. R. 2002 Aircraft viscous drag reduction using riblets. Prog. Aerosp. Sci. 38 (6–7), 571–600.Google Scholar
Vreman, A. W. 2004 An eddy-viscosity subgrid-scale model for turbulent shear flow: algebraic theory and applications. Phys. Fluids 16 (10), 3670–3681.Google Scholar
Walsh, M. J.(Ed.) 1982 Turbulent Boundary Layer Drag Reduction using Riblets, 20th AIAA Aerospace Sciences Meeting, Orlando, FL.Google Scholar
Zanoun, E.-S., Nagib, H. & Durst, F. 2009 Refined c f relation for turbulent channels and consequences for high-Re experiments. Fluid Dyn. Res. 41 (2), 021405.Google Scholar