Published online by Cambridge University Press: 28 April 2020
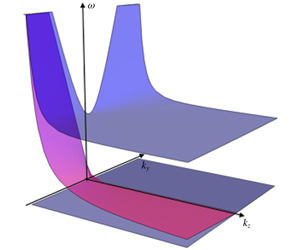
Coasts are obstructions to the classical derivation of continuously stratified quasi-geostrophic equations, due to possible resonances between slow internal coastally trapped Kelvin waves and anticyclones. Deremble et al. (Ocean Model., vol. 119, 2017, pp. 1–12) proposed a coupled model between a quasi-geostrophic interior and boundary-layer Kelvin-wave dynamics. We revisit the derivation of this model, paying particular attention to conservation laws. We find that quasi-geostrophic energy is conserved, despite the existence of Kelvin-wave shocks in the boundary layer. The effect of those shocks is to change the global distribution of potential vorticity, and, consequently, the interior flow structure. In that respect, we show that there is an active control of the boundary region on the interior flow.