Article contents
Hydrodynamic interaction of two deformable torque swimmers
Published online by Cambridge University Press: 29 April 2020
Abstract
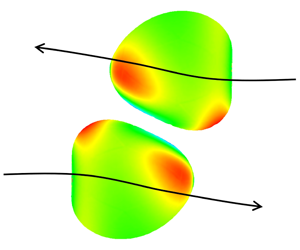
When two swimming cells collide, some ciliates show biological reactions such as avoidance and escape on sensing mechanical agitation through membrane ion channels. However, there is still no clear understanding of the mechanosensing mechanism, despite it being proposed more than 50 years ago. Moreover, it is largely unknown how the deformability of cells affects hydrodynamic interactions between microswimmers. In this study, we investigate hydrodynamic interactions between two deformable microswimmers and quantify the membrane tension during the interaction. A ciliate was modelled as a capsule with a hyperelastic membrane, and thrust generated by the cilia was modelled as torque distributed above the cell body. The model we use is the simplest we could think of that can swim, deform and exert membrane tension, such that hydrodynamic interactions can be analysed non-trivially. The results showed that softer swimmers induced smaller membrane tension during the interaction, and tended to have smaller scattering angles after the interaction. In the case of chasing interactions, swimmers attracted each other, which was not observed in non-deformable velocity squirmer models. Finally, we discuss the biological implications of these results, comparing them to those of our former experiments using Paramecium. This study is useful for understanding the effect of swimmer deformability in hydrodynamic interactions, and provides a theoretical basis for investigating a mechanical picture of the biological reactions of ciliates.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 4
- Cited by


