Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T13:26:27.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Frequency selection in a gravitationally stretched capillary jet in the jetting regime

Published online by Cambridge University Press:  29 April 2020

Isha Shukla Open the ORCID record for Isha Shukla [Opens in a new window]  and
François Gallaire Open the ORCID record for François Gallaire [Opens in a new window]
Isha Shukla
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne,1015Lausanne, Switzerland
François Gallaire*
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne,1015Lausanne, Switzerland
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

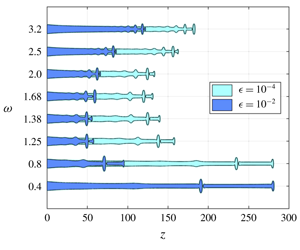
A capillary jet falling under the effect of gravity continuously stretches while thinning downstream. We report here the effect of external periodic forcing on such a spatially varying jet in the jetting regime. Surprisingly, the optimal forcing frequency producing the most unstable jet is found to be highly dependent on the forcing amplitude. Taking benefit of the one-dimensional Eggers & Dupont (J. Fluid Mech., vol. 262, 1994, pp. 205–221) equations, we investigate the case through nonlinear simulations and linear stability analysis. In the local framework, the WKBJ (Wentzel–Kramers–Brillouin–Jeffreys) formalism, established for weakly non-parallel flows, fails to capture the nonlinear simulation results quantitatively. However, in the global framework, the resolvent analysis, supplemented by a simple approximation of the required response norm inducing breakup, is shown to correctly predict the optimal forcing frequency at a given forcing amplitude and the resulting jet breakup length. The results of the resolvent analysis are found to be in good agreement with those of the nonlinear simulations.

JFM classification

Interfacial Flows (free surface): Capillary flows Instability: Absolute/convective instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 894 , 10 July 2020 , A6
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Ehrenstein, U., Gallaire, F. & Henningson, D. S. 2008 Global two-dimensional stability measures of the flat plate boundary-layer flow. Eur. J. Mech. (B/Fluids) 27 (5), 501–513.CrossRefGoogle Scholar
Alizard, F., Cherubini, S. & Robinet, J.-C. 2009 Sensitivity and optimal forcing response in separated boundary layer flows. Phys. Fluids 21 (6), 064108.CrossRefGoogle Scholar
Ambravaneswaran, B., Wilkes, E. D. & Basaran, O. A. 2002 Drop formation from a capillary tube: comparison of one-dimensional and two-dimensional analyses and occurrence of satellite drops. Phys. Fluids 14 (8), 2606–2621.CrossRefGoogle Scholar
Bank, R. E., Coughran, W. M., Fichtner, W., Grosse, E. H., Rose, D. J. & Smith, R. K. 1985 Transient simulation of silicon devices and circuits. IEEE Trans. Electron Devices 32 (10), 1992–2007.CrossRefGoogle Scholar
Basaran, O. A. 2002 Small-scale free surface flows with breakup: drop formation and emerging applications. AIChE J. 48 (9), 1842–1848.CrossRefGoogle Scholar
Basaran, O. A., Gao, H. & Bhat, P. P. 2013 Nonstandard inkjets. Annu. Rev. Fluid Mech. 45, 85–113.CrossRefGoogle Scholar
Bennett, W. D., Brown, J. S., Zeman, K. L., Hu, S.-C., Scheuch, G. & Sommerer, K. 2002 Targeting delivery of aerosols to different lung regions. J. Aerosol Med. 15 (2), 179–188.CrossRefGoogle ScholarPubMed
Boujo, E. & Gallaire, F. 2015 Sensitivity and open-loop control of stochastic response in a noise amplifier flow: the backward-facing step. J. Fluid Mech. 762, 361–392.CrossRefGoogle Scholar
Briggs, R. J. 1964 Electron-stream Interaction With Plasmas. MIT Press.CrossRefGoogle Scholar
Chaudhary, K. C. & Redekopp, L. G. 1980 The nonlinear capillary instability of a liquid jet. Part 1. Theory. J. Fluid Mech. 96 (2), 257–274.CrossRefGoogle Scholar
Consoli-Lizzi, P. A.2016 Capillary breakup of stretched liquid jets. PhD thesis, UC3M.Google Scholar
Consoli-Lizzi, P. A., Coenen, W. & Sevilla, A.2014 Experiments and non-parallel theory on the natural break-up of freely falling Newtonian liquid jets. In APS Meeting Abstracts.Google Scholar
van Deventer, H., Houben, R. & Koldeweij, R. 2013 New atomization nozzle for spray drying. Dry. Technol. 31 (8), 891–897.CrossRefGoogle Scholar
Doshi, J. & Reneker, D. H. 1995 Electrospinning process and applications of electrospun fibers. J. Electrostat. 35 (2-3), 151–160.CrossRefGoogle Scholar
Driessen, T. & Jeurissen, R. 2011 A regularised one-dimensional drop formation and coalescence model using a total variation diminishing (TVD) scheme on a single Eulerian grid. Intl J. Comput. Fluid Dyn. 25 (6), 333–343.CrossRefGoogle Scholar
Driessen, T., Sleutel, P., Dijksman, F., Jeurissen, R. & Lohse, D. 2014 Control of jet breakup by a superposition of two Rayleigh–Plateau-unstable modes. J. Fluid Mech. 749, 275–296.CrossRefGoogle Scholar
Eggers, J. & Dupont, T. F. 1994 Drop formation in a one-dimensional approximation of the Navier–Stokes equation. J. Fluid Mech. 262, 205–221.CrossRefGoogle Scholar
Eggers, J. & Villermaux, E. 2008 Physics of liquid jets. Rep. Prog. Phys. 71 (3), 036601.Google Scholar
Foures, D. P. G., Caulfield, C. P. & Schmid, P. J. 2013 Localization of flow structures using ∞-norm optimization. J. Fluid Mech. 729, 672–701.CrossRefGoogle Scholar
Frankel, I. & Weihs, D. 1985 Stability of a capillary jet with linearly increasing axial velocity (with application to shaped charges). J. Fluid Mech. 155, 289–307.CrossRefGoogle Scholar
Frankel, I. & Weihs, D. 1987 Influence of viscosity on the capillary instability of a stretching jet. J. Fluid Mech. 185, 361–383.CrossRefGoogle Scholar
Gallaire, F. & Brun, P.-T. 2017 Fluid dynamic instabilities: theory and application to pattern forming in complex media. Phil. Trans. R. Soc. Lond. A 375 (2093), 20160155.CrossRefGoogle ScholarPubMed
García, F. J. & Castellanos, A. 1994 One-dimensional models for slender axisymmetric viscous liquid jets. Phys. Fluids 6 (8), 2676–2689.CrossRefGoogle Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 The preferred mode of incompressible jets: linear frequency response analysis. J. Numer. Math. 716, 189–202.Google Scholar
Gaster, M., Kit, E. & Wygnanski, I. 1985 Large-scale structures in a forced turbulent mixing layer. J. Fluid Mech. 150, 23–39.CrossRefGoogle Scholar
Guerrero, J., González, H. & García, F. J. 2016 Spatial modes in one-dimensional models for capillary jets. Phys. Rev. E 93 (3), 033102.Google ScholarPubMed
Hilbing, J. H. & Heister, S. D. 1996 Droplet size control in liquid jet breakup. Phys. Fluids 8 (6), 1574–1581.CrossRefGoogle Scholar
van Hoeve, W., Gekle, S., Snoeijer, J. H., Versluis, M., Brenner, M. P. & Lohse, D. 2010 Breakup of diminutive Rayleigh jets. Phys. Fluids 22 (12), 122003.CrossRefGoogle Scholar
Huerre, P. & Rossi, M. 1998 Hydrodynamic Instabilities in Open Flows. Cambridge University Press.CrossRefGoogle Scholar
Javadi, A., Eggers, J., Bonn, D., Habibi, M. & Ribe, N. M. 2013 Delayed capillary breakup of falling viscous jets. Phys. Rev. Lett. 110, 144501.Google ScholarPubMed
Kowalewski, T. A. 1996 On the separation of droplets from a liquid jet. Fluid Dyn. Res. 17 (3), 121–145.CrossRefGoogle Scholar
Le Dizès, S. 1997 Global modes in falling capillary jets. Eur. J. Mech. (B/Fluids) 16, 761–778.Google Scholar
Le Dizès, S. & Villermaux, E. 2017 Capillary jet breakup by noise amplification. J. Fluid Mech. 810, 281–306.CrossRefGoogle Scholar
Leib, S. J. & Goldstein, M. E. 1986 The generation of capillary instabilities on a liquid jet. J. Fluid Mech. 168, 479–500.CrossRefGoogle Scholar
Loscertales, I. G., Barrero, A., Guerrero, I., Cortijo, R., Marquez, M. & Ganan-Calvo, A. M. 2002 Micro/nano encapsulation via electrified coaxial liquid jets. Science 295 (5560), 1695–1698.CrossRefGoogle ScholarPubMed
Mantič-Lugo, V. & Gallaire, F. 2016 Saturation of the response to stochastic forcing in two-dimensional backward-facing step flow: a self-consistent approximation. Phys. Rev. F 1 (8), 083602.Google Scholar
Marín, A. G., Campo-Cortés, F. & Gordillo, J. M. 2009 Generation of micron-sized drops and bubbles through viscous coflows. Colloid. Surf. A 344 (1–3), 2–7.CrossRefGoogle Scholar
Marquet, O. & Sipp, D. 2010 Global sustained perturbations in a backward-facing step flow. Seventh IUTAM Symp. Laminar-Turbulent Transition 18, 525–528.CrossRefGoogle Scholar
Monokrousos, A., Åkervik, E., Brandt, L. & Henningson, D. S. 2010 Global three-dimensional optimal disturbances in the Blasius boundary-layer flow using time-steppers. J. Fluid Mech. 650, 181–214.CrossRefGoogle Scholar
Nichols, J. & Lele, S.2010 Global mode analysis of turbulent high-speed jets. In Annual Research Briefs 2010, Center for Turbulence Research.Google Scholar
Nichols, J. W. & Lele, S. K. 2011 Non-normal global modes of high-speed jets. Intl J. Spray. Combust. Dyn. 3 (4), 285–301.CrossRefGoogle Scholar
Pearson, J. R. A. & Matovich, M. A. 1969 Spinning a molten threadline. Stability. Ind. Engng Chem. Res. 8 (4), 605–609.Google Scholar
Plateau, J. A. F. 1873 Statique expérimentale et théorique des liquides soumis aux seules forces moléculaires, vol. 2. Gauthier-Villars.Google Scholar
Rayleigh, Lord 1879 On the capillary phenomena of jets. Proc. R. Soc. Lond. A 29 (196–199), 71–97.Google Scholar
Rubio-Rubio, M., Sevilla, A. & Gordillo, J. M. 2013 On the thinnest steady threads obtained by gravitational stretching of capillary jets. J. Fluid Mech. 729, 471–483.CrossRefGoogle Scholar
Sauter, U. S. & Buggisch, H. W. 2005 Stability of initially slow viscous jets driven by gravity. J. Fluid Mech. 533, 237–257.CrossRefGoogle Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39 (1), 129–162.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 1994 Optimal energy density growth in Hagen–Poiseuille flow. J. Fluid Mech. 277, 197–225.CrossRefGoogle Scholar
Senchenko, S. & Bohr, T. 2005 Shape and stability of a viscous thread. Phys. Rev. E 71 (5), 056301.Google ScholarPubMed
Sevilla, A. 2011 The effect of viscous relaxation on the spatiotemporal stability of capillary jets. J. Fluid Mech. 684, 204–226.CrossRefGoogle Scholar
Shimozuru, D. 1994 Physical parameters governing the formation of Pele’s hair and tears. Bull. Volcanol. 56 (3), 217–219.CrossRefGoogle Scholar
Sipp, D. & Marquet, O. 2013 Characterization of noise amplifiers with global singular modes: the case of the leading-edge flat-plate boundary layer. Theor. Comput. Fluid Dyn. 27 (5), 617–635.CrossRefGoogle Scholar
Spalding, D. B. 1972 A novel finite difference formulation for differential expressions involving both first and second derivatives. Intl J. Numer. Meth. Engng 4 (4), 551–559.CrossRefGoogle Scholar
Tomotika, S. 1936 Breaking up of a drop of viscous liquid immersed in another viscous fluid which is extending at a uniform rate. Proc. R. Soc. Lond. A 153 (879), 302–318.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.CrossRefGoogle ScholarPubMed
Viola, F., Arratia, C. & Gallaire, F. 2016 Mode selection in trailing vortices: harmonic response of the non-parallel batchelor vortex. J. Fluid Mech. 790, 523–552.CrossRefGoogle Scholar
Wijshoff, H. 2010 The dynamics of the piezo inkjet printhead operation. Phys. Rep. 491 (4–5), 77–177.Google Scholar