Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-19T23:59:49.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow over a flat plate with uniform inlet and incident coherent gusts

Published online by Cambridge University Press:  27 February 2013

Imran Afgan ,
Sofiane Benhamadouche ,
Xingsi Han ,
Pierre Sagaut  and
Dominique Laurence
Imran Afgan*
Affiliation:
Institut Jean Le Rond d’Alembert, Université Pierre et Marie Curie-Paris VI, 4 place Jussieu – case 162, 75252 Paris, France Modelling & Simulation Centre, School of MACE, University of Manchester, M13 9PL, UK Department of Mechanical & Aerospace Engineering, Air University, E-9, Islamabad
Sofiane Benhamadouche
Affiliation:
Mécanique des Fluides Energies et Environnement (MFEE), EDF - R&D, 6 quai Watier, 78401 Chatou, France LaMSID, UMR CNRS EDF 2832, Clamart, France
Xingsi Han
Affiliation:
Institut Jean Le Rond d’Alembert, Université Pierre et Marie Curie-Paris VI, 4 place Jussieu – case 162, 75252 Paris, France
Pierre Sagaut
Affiliation:
Institut Jean Le Rond d’Alembert, Université Pierre et Marie Curie-Paris VI, 4 place Jussieu – case 162, 75252 Paris, France
Dominique Laurence
Affiliation:
Modelling & Simulation Centre, School of MACE, University of Manchester, M13 9PL, UK Mécanique des Fluides Energies et Environnement (MFEE), EDF - R&D, 6 quai Watier, 78401 Chatou, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

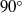The flow over a flat plate at a Reynolds number of 750 is numerically investigated via fine large-eddy simulation (LES), first at normal ($90\textdegree $) and then at oblique (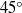$45\textdegree $) incidence flow direction with a uniform steady inlet. The results are in complete agreement with the direct numerical simulation (DNS) and experimental data, thereby serving as a validation for the present simulations. For the normal (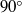$90\textdegree $) uniform inflow case, coherent vortices are alternately shed from both leading edges of the plate, whereas for the oblique (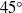$45\textdegree $) uniform inflow case the vortices shed from the two sides of the plate interact strongly resulting in a quasi-periodic force response. The normal flat plate is then analysed with an incident gust signal with varying amplitude and time period. For these incident coherent gust cases, a reference test case with variable coherent inlet is first studied and the results are compared to a steady inlet simulation, with a detailed analysis of the flow behaviour and the wake response under the incident gust. Finally, the flat plate response to 16 different gust profiles is studied. A transient drag reconstruction for these incident coherent gust cases is then presented based on a frequency-dependent transfer function and phase spectrum analysis.

JFM classification

Flow Control: Flow Control Turbulent Flows: Turbulent Flows Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 457 - 485
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afgan, I., Kahil, Y., Benhamadouche, S. & Sagaut, P. 2011 Lareg Eddy Simulation of the flow around single and two side-by-side cylinders at subcritical Reynolds numbers. Phys. Fluids 23, 075101.Google Scholar
Afgan, I., Moulinec, C., Prosser, R. & Laurence, D. 2007 Large Eddy Simulation of turbulent flow for wall mounted cantilever cylinders of aspect ratio 6 and 10. Intl J. Heat Fluid Flow 28, 561–574.Google Scholar
Archambeau, F., Mchitoua, N. & Sakiz, M. 2004 Code_Saturne: a finite volume code for the computation of turbulent incompressible flows-industrial applications. Intl J. Finite Vol. 1, ISSN 1634(0655).Google Scholar
Bearman, P. W. 1971 Investigation of forces on flat plate normal to a turbulent flow. J. Fluid. Mech. 46, 177–198.Google Scholar
Benhamadouche, S., Laurence, D., Jarrin, N., Afgan, I. & Moulinec, C. 2005 Large Eddy Simulation of flow across in-line tube bundles. In Nuclear Reactor Thermal Hydraulics, NURETH-11. Avignon, France. Paper 405.Google Scholar
Bierbooms, W. 2004 A gust model for wind turbine design. JSME Intl J. B 47 (2), 378–386.Google Scholar
Bierbooms, W. & Cheng, P.-W. 2002 Stochastic gust model for design calculation of wind turbine. J. Wind Engng Ind. Aerodyn. 90, 1237–1251.CrossRefGoogle Scholar
Breuer, M. & Jovicic, N. 2001 Separated flow around a flat plate at high incidence: an LES investigation. J. Turbul. 2 (18).Google Scholar
Chen, J. M. & Fang, Y.-C. 1996 Strouhal numbers of inclined flat plates. J. Wind Engng Ind. Aerodyn. 61, 99–112.Google Scholar
Davenport, A. G. 1961 The application of statistical concepts to the wind loading of structures. Proc. Inst. Civil Engrs 19, 449–472.Google Scholar
Davenport, A. G. 1967 Gust loading factors. J. Struct. Div. 93 (3), 11–34.Google Scholar
Dennis, S. C. R., Wang-Qiang, C. M. & Launay, J. L. 1993 Viscous flow normal to a flat plate at moderate Reynolds numbers. J. Fluid Mech. 248, 605–635.Google Scholar
Drabble, M. J., Grant, I., Armstrong, B. J. & Barnes, F. H. 1990 The aerodynamic admittance of a square plate in a flow with a fully coherent fluctuation. Phys. Fluids A 2 (6), 1005–1013.Google Scholar
Fage, A. & Johansen, F. C. 1927 On the flow of air behind an inclined flat plate of infinite span. Proc. R. Soc. Lond. A 116 (773), 170–197.Google Scholar
Fox, T. A. & West, G. S. 1990 On the use of end plates with circular cylinders. Exp. Fluids 9, 231–239.Google Scholar
Goyette, S., Brasseur, O. & Beniston, M. 2003 Application of a new wind gust parametrization: multi-scale case studies performed with the Canadian regional climate model. J. Geophys. Res. 108 (D13), 4374.Google Scholar
Harper, B. A., Kepert, J. D. & Ginger, J. D. 2008 Guidelines for converting between various wind averaging periods in tropical cyclone conditions. World Meteorological Organization Report. Appendix II.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, stream and convergence zones in turbulent flows. Report CTR-S88. Center for Turbulent Research, Stanford University.Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.Google Scholar
Julien, S., Lasheras, J. & Chomaz, J.-M. 2003 Three-dimensional instability and vorticity patters in the wake of a flat plate. J. Fluid Mech. 479, 155–189.CrossRefGoogle Scholar
Julien, S., Ortiz, S. & Chomaz, J.-M. 2004 Secondary instability mechanisms in the wake of a flat plate. Eur. J. Mech. B/Fluids 23, 157–165.Google Scholar
Kim, D. H., Yang, K. S. & Senda, M. 2004 Large eddy simulation of turbulent flow past a square cylinder confined in a channel. Comput. Fluids 33, 81–966.Google Scholar
Kiya, M. & Matsumura, M. 1988 Incoherent turbulence structure in the near wake of a normal plate. J. Fluid Mech. 190, 157–165.Google Scholar
Koumoutsakos, P. & Shiels, D. 1996 Simulations of the viscous flow normal to an impulsively started and uniformly accelerated flat plate. J. Fluid Mech. 328, 177–227.Google Scholar
Lamont, P. J. & Hunt, B. L. 1980 The impingement of underexpanded, axisymmetric jets on perpendicular and inclined flat plates. J. Fluid Mech. 100, 471–511.Google Scholar
Leder, A. 1991 Dynamics of fluid mixing in separated flows. Phys. Fluids A 3 (7), 1741–1748.CrossRefGoogle Scholar
Lighthill, M. J. 1954 The response of laminar skin friction and heat transfer to fluctuations in the stream velocity. Proc. R. Soc. Lond. A 224, 1–23.Google Scholar
Mazharoǧlu, Ç. & Hacışevki, H. 1999 Coherent and incoherent flow structures behind a normal flat plate. Exp. Therm. Fluid Sci. 19, 160–167.Google Scholar
Moser, R. & Balachandar, S. 1998 Self-similarity of time-evolving plane wakes. J. Fluid Mech. 367, 255–289.Google Scholar
Moulinec, C., Benhamadouche, S., Laurence, D. & Peric, M. 2005 LES in a U-bend pipe meshed by polyhedral cells. In ERCOFTAC ETMM-6 Conference. Elsevier.Google Scholar
Najjar, F. M. & Balachandar, S. 1998 Low frequency unsteadiness in the wake of a normal flat plate. J. Fluid Mech. 370, 101–147.Google Scholar
Najjar, F. M. & Vanka, S. P. 1995a Simulations of the unsteady separated flow past a normal flat plate. Intl J. Numer. Meth. Fluids 21, 525–547.Google Scholar
Najjar, F. M. & Vanka, S. P. 1995b Effects of intrinsic three-dimensionality on the drag characteristics of a normal flat plate. Phys. Fluids 7 (10), 2516–2518.Google Scholar
Nakagawa, S., Nitta, K. & Senda, M. 1999 An experimental study on unsteady turbulent near wake of a rectangular cylinder in channel flow. Exp. Fluids 27 (3), 284–294.CrossRefGoogle Scholar
Narasimhamurthy, V. D. & Andersson, H. I. 2009 Numerical simulation of the turbulent wake behind a normal flat plate. Intl J. Heat Fluid Flow 30, 1037–1043.Google Scholar
Norberg, C. 1994 An experimental investigation of the flow around a circular cylinder: influence of aspect ratio. J. Fluid Mech. 258, 287–316.CrossRefGoogle Scholar
Norberg, C. 2003 Fluctuating lift on a circular cylinder: review and new measurements. J. Fluids Struct. 17, 57–96.CrossRefGoogle Scholar
Pagnini, L. C. & Solari, G. 2002 Gust buffeting and turbulence uncertainties. J. Wind Engng Ind. Aerodyn. 90, 441–459.Google Scholar
Perry, A. E. & Steiner, T. R. 1987 Large-scale vortex structures in turbulent wakes behind bluff bodies. Part 1. Vortex formation processes. J. Fluid Mech. 174, 233–270.Google Scholar
Press, W. H, Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1996 Numerical Recipes in Fortran 77: Vol 1: The Art of Scientific Computing, 2nd edn. Cambridge University Press, ISBN: 0-521-43064-X.Google Scholar
Quinn, A. D., Baker, C. J. & Wright, N. G. 2001 Wind and vehicle induced forces on flat plates–Part 1: wind induced force. J. Wind Engng Ind. Aerodyn. 89, 817–829.Google Scholar
Rhie, C. & Chow, W. 1982 A numerical study of the flow past an isolated aerofoil with trailing edge separation. AIAA J. 21, 1525–1532.CrossRefGoogle Scholar
Roshko, A. 1993 Prespectives on bluff body aerodynamics. J. Wind Engng Ind. Aerodyn. 49, 79–100.Google Scholar
Saha, A. K. 2007 Far-wake characteristics of two-dimensional flow past a normal flat plate. Phys. Fluids 19, 128110.CrossRefGoogle Scholar
Solari, G. & Piccardo, G. 2000 Probabilistic 3-D turbulence modelling for gust buffeting of structures. Prob. Engng Mech. 16, 73–86.CrossRefGoogle Scholar
Steiner, T. R. & Perry, A. E. 1987 Large-scale vortex structures in turbulent wakes behind buff bodies. Part 2. Far-wake structures. J. Fluid Mech. 174, 271–298.Google Scholar
Tamaddon-Jahromi, H. R., Townsend, P. & Webster, M. F. 1994 Unsteady viscous flow past a flat plate orthogonal to the flow. Comput. Fluids 23 (2), 433–446.Google Scholar
Thompson, M. C., Hourigan, K., Ryan, K. & Sheard, G. J. 2006 Wake transition of two-dimensional cylinders and axisymmetric bluff bodies. J. Fluids Struct. 22, 793–806.Google Scholar
Van Doormal, J. P. & Raithby, G. D. 1984 Enhancements of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transfer 7, 147–163.Google Scholar
Vickery, B. J. 1965 On the flow behind a coarse grid and its use as a model of atmospheric turbulence in studies related to wind loads in buildings. National Physical Laboratory. Aero Rep. No. 1143.Google Scholar
Wu, S. J., Miau, J. J., Hu, C. C. & Chou, J. H. 2005 On low-frequency modulations and three-dimensionality in vortex shedding behind a normal plate. J. Fluid Mech. 526, 117–146.Google Scholar
Yao, Y. F., Thomas, T. G., Sandham, N. D. & Williams, J. J. R. 2001 Direct numerical simulation of turbulent flow over a rectangular trailing edge. Theor. Comput. Fluid Dyn. 14, 337–358.CrossRefGoogle Scholar
Yeung, W. W. H. & Parkinson, G. V. 1997 On the steady separated flow around and inclined flat plate. J. Fluid Mech. 333, 403–413.Google Scholar