Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Park, Beomchan
and
Cho, Yeunwoo
2018.
Two-dimensional gravity–capillary solitary waves on deep water: generation and transverse instability.
Journal of Fluid Mechanics,
Vol. 834,
Issue. ,
p.
92.
Cho, Yeunwoo
2018.
Long-time behavior of three-dimensional gravity-capillary solitary waves on deep water generated by a moving air-blowing forcing: Numerical study.
Physical Review E,
Vol. 98,
Issue. 3,
Tomlin, Ruben J.
Gomes, Susana N.
Pavliotis, Grigorios A.
and
Papageorgiou, Demetrios T.
2019.
Optimal Control of Thin Liquid Films and Transverse Mode Effects.
SIAM Journal on Applied Dynamical Systems,
Vol. 18,
Issue. 1,
p.
117.
Abid, M.
Kharif, C.
Hsu, H.-C.
and
Chen, Y.-Y.
2019.
Transverse instability of gravity–capillary solitary waves on deep water in the presence of constant vorticity.
Journal of Fluid Mechanics,
Vol. 871,
Issue. ,
p.
1028.
Park, Beomchan
and
Cho, Yeunwoo
2020.
Hysteresis phenomena in gravity–capillary waves on deep water generated by a moving two-dimensional/three-dimensional air-blowing/air-suction forcing.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Li, Shaofeng
Song, Jinbao
and
Cao, Anzhou
2020.
Gravity-capillary waves modulated by linear shear flow in arbitrary water depth*
.
Chinese Physics B,
Vol. 29,
Issue. 12,
p.
124702.
Lunz, Davin
2021.
Minimizing deformation of a thin fluid film driven by fluxes of momentum and heat.
Physical Review E,
Vol. 103,
Issue. 3,
Stevenson, Noah
and
Tice, Ian
2021.
Traveling Wave Solutions to the Multilayer Free Boundary Incompressible Navier--Stokes Equations.
SIAM Journal on Mathematical Analysis,
Vol. 53,
Issue. 6,
p.
6370.
Leoni, Giovanni
and
Tice, Ian
2023.
Traveling Wave Solutions to the Free Boundary Incompressible Navier‐Stokes Equations.
Communications on Pure and Applied Mathematics,
Vol. 76,
Issue. 10,
p.
2474.
Cho, Yeunwoo
2023.
Analytic calculation of two-dimensional linear viscous gravity–capillary waves on deep water generated by a moving forcing at non-critical conditions: wave patterns and spatial decay rate.
Journal of Engineering Mathematics,
Vol. 139,
Issue. 1,
Stevenson, Noah
and
Tice, Ian
2024.
Well-posedness of the stationary and slowly traveling wave problems for the free boundary incompressible Navier-Stokes equations.
Journal of Functional Analysis,
Vol. 287,
Issue. 11,
p.
110617.
Brownfield, John
and
Nguyen, Huy Q.
2024.
Slowly Traveling Gravity Waves for Darcy Flow: Existence and Stability of Large Waves.
Communications in Mathematical Physics,
Vol. 405,
Issue. 10,
Cho, Yeunwoo
2024.
Gravity–capillary wave-making resistance on deep water.
Physics of Fluids,
Vol. 36,
Issue. 1,
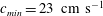 $c_{min}=23~\text{cm}~\text{s}^{-1}$. Three different states are observed according to forcing speeds below
$c_{min}=23~\text{cm}~\text{s}^{-1}$. Three different states are observed according to forcing speeds below 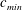 $c_{min}$. At relatively low speeds below
$c_{min}$. At relatively low speeds below 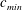 $c_{min}$, small-amplitude linear circular depressions are observed, and they move steadily ahead of and along with the moving forcing. As the forcing speed increases close to
$c_{min}$, small-amplitude linear circular depressions are observed, and they move steadily ahead of and along with the moving forcing. As the forcing speed increases close to 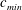 $c_{min}$, however, nonlinear three-dimensional (3-D) gravity–capillary solitary waves are observed, and they move steadily ahead of and along with the moving forcing. Finally, when the forcing speed is very close to
$c_{min}$, however, nonlinear three-dimensional (3-D) gravity–capillary solitary waves are observed, and they move steadily ahead of and along with the moving forcing. Finally, when the forcing speed is very close to 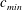 $c_{min}$, oblique shedding phenomena of 3-D gravity–capillary solitary waves are observed ahead of the moving forcing. We found that all the linear and nonlinear wave patterns generated by the air-suction forcing correspond to those generated by the air-blowing forcing. The main difference is that 3-D gravity–capillary solitary waves are observed ‘ahead of’ the air-suction forcing whereas the same waves are observed ‘behind’ the air-blowing forcing.
$c_{min}$, oblique shedding phenomena of 3-D gravity–capillary solitary waves are observed ahead of the moving forcing. We found that all the linear and nonlinear wave patterns generated by the air-suction forcing correspond to those generated by the air-blowing forcing. The main difference is that 3-D gravity–capillary solitary waves are observed ‘ahead of’ the air-suction forcing whereas the same waves are observed ‘behind’ the air-blowing forcing.