Research Article
Financial Structure and Cost of Capital in the Multinational Corporation
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 211-226
-
- Article
- Export citation
On the Financing and Investment Decisions of Multinational Firms in the Presence of Exchange Risk
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 227-244
-
- Article
- Export citation
Optimal Foreign Borrowing Strategies with Operations in Forward Exchange Markets
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 245-254
-
- Article
- Export citation
Safety-First, Stochastic Dominance, and Optimal Portfolio Choice
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 255-271
-
- Article
- Export citation
The Inference of Tastes and Beliefs from Bond and Stock Market Data
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 273-297
-
- Article
- Export citation
Effects of Measurement Errors on Systematic Risk and Performance Measure of a Portfolio
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 299-312
-
- Article
- Export citation
The Effect of Intervaling on Estimating Parameters of the Capital Asset Pricing Model
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 313-332
-
- Article
- Export citation
Some Problems in Applying the Continuous Portfolio Selection Model to the Discrete Capital Budgeting Problem
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 333-344
-
- Article
- Export citation
Equivalent Mathematical Programming Models of Pure Capital Rationing
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 345-361
-
- Article
- Export citation
The Unique, Real Internal Rate of Return: Caveat Emptor!
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 363-370
-
- Article
- Export citation
Letter
An Analytical Model of Bond Risk Differentials: A Comment
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 371-377
-
- Article
-
- You have access
- Export citation
Reply
An Analytical Model of Bond Risk Differentials: A Reply
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 379-381
-
- Article
- Export citation
Announcement
Announcement
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. 382-383
-
- Article
-
- You have access
- Export citation
Front matter
JFQ volume 13 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 April 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation

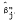 , and the Jensen's measure of performance,
, and the Jensen's measure of performance, 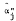 . In Section III, we derive an analytical expression for the regression coefficient of estimated b's where we estimate the equation
. In Section III, we derive an analytical expression for the regression coefficient of estimated b's where we estimate the equation 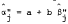 . The result is then examined to find the conditions under which errors in measurement of R
. The result is then examined to find the conditions under which errors in measurement of R