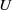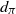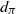1. Introduction and main results
In this paper we use the Stein method to estimate the Wasserstein distance between a nonnegative integer-valued random vector and a Poisson random vector. This problem has been studied by several authors, mostly in terms of the total variation distance; among others we mention [Reference Arratia, Goldstein and Gordon1, Reference Barbour3, Reference Barbour4, Reference Barbour, Holst and Janson6, Reference Čekanavičius and Vellaisamy13, Reference Roos28, Reference Roos29]. Furthermore, we use our abstract result on multivariate Poisson approximation to derive a limit theorem for the Poisson process approximation.
More precisely, let
![]() $\textbf{X}=(X_1,\dots ,X_d)$
be an integrable random vector taking values in
$\textbf{X}=(X_1,\dots ,X_d)$
be an integrable random vector taking values in
![]() $\mathbb N_0^d$
,
$\mathbb N_0^d$
,
![]() $d\in\mathbb N$
, where
$d\in\mathbb N$
, where
![]() $\mathbb N_0=\mathbb N\cup \!\{0\}$
, and let
$\mathbb N_0=\mathbb N\cup \!\{0\}$
, and let
![]() $\textbf{P}=(P_1,\dots ,P_d)$
be a Poisson random vector, that is, a random vector with independent and Poisson distributed components. The first contribution of this paper is an upper bound on the Wasserstein distance
$\textbf{P}=(P_1,\dots ,P_d)$
be a Poisson random vector, that is, a random vector with independent and Poisson distributed components. The first contribution of this paper is an upper bound on the Wasserstein distance
between
![]() $\textbf{X}$
and
$\textbf{X}$
and
![]() $\textbf{P}$
, where
$\textbf{P}$
, where
![]() $\textrm{Lip}^d(1)$
denotes the set of Lipschitz functions
$\textrm{Lip}^d(1)$
denotes the set of Lipschitz functions
![]() $g\;:\;\mathbb N_0^d \rightarrow \mathbb R$
with Lipschitz constant bounded by 1 with respect to the metric induced by the 1-norm
$g\;:\;\mathbb N_0^d \rightarrow \mathbb R$
with Lipschitz constant bounded by 1 with respect to the metric induced by the 1-norm
![]() $|\textbf{x}|_1= \sum_{i=1}^d |x_i|$
, for
$|\textbf{x}|_1= \sum_{i=1}^d |x_i|$
, for
![]() $\textbf{x}=(x_1,\dots,x_d)\in\mathbb R^d$
. Note that, since the indicator functions defined on
$\textbf{x}=(x_1,\dots,x_d)\in\mathbb R^d$
. Note that, since the indicator functions defined on
![]() $\mathbb N_0^d$
are Lipschitz continuous, for random vectors in
$\mathbb N_0^d$
are Lipschitz continuous, for random vectors in
![]() $\mathbb N_0^d$
the Wasserstein distance dominates the total variation distance, and it is not hard to find sequences that converge in total variation distance but not in Wasserstein distance. Our goal is to extend the approach developed in [Reference Pianoforte and Schulte25] for the Poisson approximation of random variables to the multivariate case.
$\mathbb N_0^d$
the Wasserstein distance dominates the total variation distance, and it is not hard to find sequences that converge in total variation distance but not in Wasserstein distance. Our goal is to extend the approach developed in [Reference Pianoforte and Schulte25] for the Poisson approximation of random variables to the multivariate case.
Throughout the paper, for any
![]() $\textbf{x}=(x_1,\dots,x_d)\in\mathbb R^d$
and index
$\textbf{x}=(x_1,\dots,x_d)\in\mathbb R^d$
and index
![]() $1\leq j\leq d$
, we denote by
$1\leq j\leq d$
, we denote by
![]() $x_{1:j}$
and
$x_{1:j}$
and
![]() $x_{j:d}$
the subvectors
$x_{j:d}$
the subvectors
![]() $(x_1,\dots,x_j)$
and
$(x_1,\dots,x_j)$
and
![]() $(x_j,\dots,x_d)$
, respectively.
$(x_j,\dots,x_d)$
, respectively.
Theorem 1.1. Let
![]() $\textbf{X}=(X_1,\dots ,X_d)$
be an integrable random vector with values in
$\textbf{X}=(X_1,\dots ,X_d)$
be an integrable random vector with values in
![]() $\mathbb N_0^d$
,
$\mathbb N_0^d$
,
![]() $d\in\mathbb N$
, and let
$d\in\mathbb N$
, and let
![]() $\textbf{P}=(P_1,\dots , P_d)$
be a Poisson random vector with
$\textbf{P}=(P_1,\dots , P_d)$
be a Poisson random vector with
![]() $\mathbb E[\textbf{P}]=(\lambda_1,\dots,\lambda_d)\in [0,\infty)^d$
. For
$\mathbb E[\textbf{P}]=(\lambda_1,\dots,\lambda_d)\in [0,\infty)^d$
. For
![]() $1\leq i\leq d$
, consider any random vector
$1\leq i\leq d$
, consider any random vector
![]() $\textbf{Z}^{(i)}= \left(Z^{(i)}_1,\dots,Z^{(i)}_i \right)$
in
$\textbf{Z}^{(i)}= \left(Z^{(i)}_1,\dots,Z^{(i)}_i \right)$
in
![]() $\mathbb Z^i$
defined on the same probability space as
$\mathbb Z^i$
defined on the same probability space as
![]() $\textbf{X}$
, and define
$\textbf{X}$
, and define
for
![]() $m_{1:i}\in\mathbb N_0^{i}$
with
$m_{1:i}\in\mathbb N_0^{i}$
with
![]() $m_i\neq0$
. Then
$m_i\neq0$
. Then
 \begin{equation} d_W(\textbf{X},\textbf{P})\leq\sum_{i=1}^d\left(\lambda_i \mathbb E\big|Z^{(i)}_i\big| +2\lambda_i\sum_{j=1}^{i-1}\mathbb E\big|Z^{(i)}_j\big| +\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}} \left|q_{m_{1:i}}\right|\right). \end{equation}
\begin{equation} d_W(\textbf{X},\textbf{P})\leq\sum_{i=1}^d\left(\lambda_i \mathbb E\big|Z^{(i)}_i\big| +2\lambda_i\sum_{j=1}^{i-1}\mathbb E\big|Z^{(i)}_j\big| +\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}} \left|q_{m_{1:i}}\right|\right). \end{equation}
It should be noted that a bound that slightly improves (1.2) can easily be obtained as shown in the following section in Remark 2.1, which corresponds to (1.8) in [Reference Pianoforte and Schulte25, Theorem 1.3] when
![]() $d=1$
.
$d=1$
.
In order to give an interpretation of Equation (1.1), let us consider the random vectors
with
![]() $\textbf{X}$
and
$\textbf{X}$
and
![]() $\textbf{Z}^{(i)}$
defined as in Theorem 1.1. Under the additional condition
$\textbf{Z}^{(i)}$
defined as in Theorem 1.1. Under the additional condition
![]() $\mathbb P(X_{1:i}+\textbf{Z}^{(i)}\in\mathbb N_0^i)=1$
, a sequence of real numbers
$\mathbb P(X_{1:i}+\textbf{Z}^{(i)}\in\mathbb N_0^i)=1$
, a sequence of real numbers
![]() $q_{m_{1:i}}$
,
$q_{m_{1:i}}$
,
![]() $m_{1:i}\in\mathbb N_0^{i}$
with
$m_{1:i}\in\mathbb N_0^{i}$
with
![]() $m_i\neq0$
satisfies Equation (1.1) if and only if
$m_i\neq0$
satisfies Equation (1.1) if and only if
for all functions
![]() $f\;:\;\mathbb N_0^i\to\mathbb R$
such that
$f\;:\;\mathbb N_0^i\to\mathbb R$
such that
![]() $\mathbb E\left|X_i f(X_{1:i})\right|<\infty$
, where to prove that (1.4) implies (1.1) it is enough to consider f to be the function with value 1 at
$\mathbb E\left|X_i f(X_{1:i})\right|<\infty$
, where to prove that (1.4) implies (1.1) it is enough to consider f to be the function with value 1 at
![]() $m_{1:i}$
and 0 elsewhere. When the
$m_{1:i}$
and 0 elsewhere. When the
![]() $q_{m_{1:i}}$
are all zeros and
$q_{m_{1:i}}$
are all zeros and
![]() $\mathbb E[X_i]=\lambda_i$
, the condition
$\mathbb E[X_i]=\lambda_i$
, the condition
![]() $\mathbb P(X_{1:i}+\textbf{Z}^{(i)}\in\mathbb N_0^i)=1$
is satisfied, as can be seen by taking the sum over
$\mathbb P(X_{1:i}+\textbf{Z}^{(i)}\in\mathbb N_0^i)=1$
is satisfied, as can be seen by taking the sum over
![]() $m_{1:i}\in\mathbb N_0^{i}$
with
$m_{1:i}\in\mathbb N_0^{i}$
with
![]() $m_i\neq0$
in (1.1). In this case, (1.4) becomes
$m_i\neq0$
in (1.1). In this case, (1.4) becomes
Recall that, for a random variable
![]() $X\geq 0$
with mean
$X\geq 0$
with mean
![]() $\mathbb E[X]>0$
, a random variable
$\mathbb E[X]>0$
, a random variable
![]() $X^s$
has the size bias distribution of X if it satisfies
$X^s$
has the size bias distribution of X if it satisfies
for all measurable
![]() $f\;:\;\mathbb R\to\mathbb R$
such that
$f\;:\;\mathbb R\to\mathbb R$
such that
![]() $\mathbb E\left|X f(X)\right|<\infty$
. Therefore, if for some
$\mathbb E\left|X f(X)\right|<\infty$
. Therefore, if for some
![]() $1\leq i\leq d$
the
$1\leq i\leq d$
the
![]() $q_{m_{1:i}}$
are all zeros and
$q_{m_{1:i}}$
are all zeros and
![]() $\mathbb E[X_i]=\lambda_i$
, the distribution of the random vector
$\mathbb E[X_i]=\lambda_i$
, the distribution of the random vector
![]() $\textbf{Y}^{(i)}$
can be seen as the size bias distribution of
$\textbf{Y}^{(i)}$
can be seen as the size bias distribution of
![]() $X_{1:i}$
, as it satisfies (1.5), which corresponds to (1.6) in the one-dimensional case. Note that this definition is similar to that of
$X_{1:i}$
, as it satisfies (1.5), which corresponds to (1.6) in the one-dimensional case. Note that this definition is similar to that of
![]() $\textbf{X}$
-size bias distribution in the ith coordinate introduced in [Reference Goldstein and Rinott15].
$\textbf{X}$
-size bias distribution in the ith coordinate introduced in [Reference Goldstein and Rinott15].
Following this interpretation, when
![]() $\mathbb E[\textbf{X}]=(\lambda_1,\dots,\lambda_d)$
and the random vectors
$\mathbb E[\textbf{X}]=(\lambda_1,\dots,\lambda_d)$
and the random vectors
![]() $\textbf{Z}^{(i)}$
are chosen to be such that the
$\textbf{Z}^{(i)}$
are chosen to be such that the
![]() $q_{m_{1:i}}^{(i)}$
are not zero, we can think of the distribution of
$q_{m_{1:i}}^{(i)}$
are not zero, we can think of the distribution of
![]() $\textbf{Y}^{(i)}$
defined by (1.3) as an approximate size bias distribution of
$\textbf{Y}^{(i)}$
defined by (1.3) as an approximate size bias distribution of
![]() $X_{1:i}$
, where instead of assuming that
$X_{1:i}$
, where instead of assuming that
![]() $\textbf{Y}^{(i)}$
satisfies (1.5) exactly, we allow error terms
$\textbf{Y}^{(i)}$
satisfies (1.5) exactly, we allow error terms
![]() $q_{m_{1:i}}$
. This is an important advantage of Theorem 1.1, since one does not need to find random vectors with an exact size bias distribution (in the sense of (1.5)); it only matters that the error terms
$q_{m_{1:i}}$
. This is an important advantage of Theorem 1.1, since one does not need to find random vectors with an exact size bias distribution (in the sense of (1.5)); it only matters that the error terms
![]() $q_{m_{1:i}}^{(i)}$
are sufficiently small and that the random vectors
$q_{m_{1:i}}^{(i)}$
are sufficiently small and that the random vectors
![]() $\textbf{Z}^{(i)}$
are the null vectors with high probability.
$\textbf{Z}^{(i)}$
are the null vectors with high probability.
The second main contribution of our work concerns Poisson process approximation of point processes with finite intensity measure. For a point process
![]() $\xi$
and a Poisson process
$\xi$
and a Poisson process
![]() $\eta$
on a measurable space
$\eta$
on a measurable space
![]() $\mathbb X$
with finite intensity measure, Theorem 1.1 provides bounds on the Wasserstein distance
$\mathbb X$
with finite intensity measure, Theorem 1.1 provides bounds on the Wasserstein distance
where
![]() $A_1,\dots,A_d$
are measurable subsets of
$A_1,\dots,A_d$
are measurable subsets of
![]() $\mathbb X$
. This allows for a way to compare the distributions of
$\mathbb X$
. This allows for a way to compare the distributions of
![]() $\xi$
and
$\xi$
and
![]() $\eta$
, by taking the supremum of the Wasserstein distances between the point processes evaluated on arbitrary collections
$\eta$
, by taking the supremum of the Wasserstein distances between the point processes evaluated on arbitrary collections
![]() $(A_1,\dots,A_d)$
of disjoint sets. More precisely, let
$(A_1,\dots,A_d)$
of disjoint sets. More precisely, let
![]() $(\mathbb X,\mathcal X)$
be a measurable space and define
$(\mathbb X,\mathcal X)$
be a measurable space and define
![]() $\mathsf N_\mathbb X$
as the collection of all
$\mathsf N_\mathbb X$
as the collection of all
![]() $\sigma$
-finite counting measures. The set
$\sigma$
-finite counting measures. The set
![]() $\mathsf N_\mathbb X$
is equipped with the
$\mathsf N_\mathbb X$
is equipped with the
![]() $\sigma$
-field
$\sigma$
-field
![]() $\mathcal N_\mathbb X$
generated by the collection of all subsets of
$\mathcal N_\mathbb X$
generated by the collection of all subsets of
![]() $\mathsf N_\mathbb X$
of the form
$\mathsf N_\mathbb X$
of the form
This means that
![]() $\mathcal N_\mathbb X$
is the smallest
$\mathcal N_\mathbb X$
is the smallest
![]() $\sigma$
-field on
$\sigma$
-field on
![]() $\mathsf N_\mathbb X$
that makes the map
$\mathsf N_\mathbb X$
that makes the map
![]() $\nu\mapsto \nu(B)$
measurable for all
$\nu\mapsto \nu(B)$
measurable for all
![]() $B\in\mathcal X$
. A point process
$B\in\mathcal X$
. A point process
![]() $\xi$
on
$\xi$
on
![]() $\mathbb X$
is a random element in
$\mathbb X$
is a random element in
![]() $(\mathsf N_\mathbb X,\mathcal N_\mathbb X)$
. The intensity of
$(\mathsf N_\mathbb X,\mathcal N_\mathbb X)$
. The intensity of
![]() $\xi$
is the measure
$\xi$
is the measure
![]() $\lambda$
on
$\lambda$
on
![]() $(\mathbb X,\mathcal X)$
defined by
$(\mathbb X,\mathcal X)$
defined by
![]() $\lambda(B)=\mathbb E[\xi(B)]$
,
$\lambda(B)=\mathbb E[\xi(B)]$
,
![]() $B\in\mathcal X$
. When a point process
$B\in\mathcal X$
. When a point process
![]() $\xi$
has finite intensity measure
$\xi$
has finite intensity measure
![]() $\lambda$
, for any choice of subsets
$\lambda$
, for any choice of subsets
![]() $A_1,\dots,A_d\in\mathcal X$
, the random vector
$A_1,\dots,A_d\in\mathcal X$
, the random vector
![]() $(\xi(A_1),\dots,\xi(A_d))$
takes values in
$(\xi(A_1),\dots,\xi(A_d))$
takes values in
![]() $\mathbb N_0^d$
(almost surely). Thus, we define a metric in the space of point processes with finite intensity measure in the following way.
$\mathbb N_0^d$
(almost surely). Thus, we define a metric in the space of point processes with finite intensity measure in the following way.
Definition 1.1. Let
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
be point processes on
$\zeta$
be point processes on
![]() $\mathbb X$
with finite intensity measure. The distance
$\mathbb X$
with finite intensity measure. The distance
![]() $d_\pi$
between the distributions of
$d_\pi$
between the distributions of
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
is defined as
$\zeta$
is defined as
where
The function
![]() $d_\pi$
is a probability distance between the distributions of point processes, which follows immediately from its definition and, e.g., [Reference Last and Penrose19, Proposition 2.10]. To the best of our knowledge, this is the first time the distance
$d_\pi$
is a probability distance between the distributions of point processes, which follows immediately from its definition and, e.g., [Reference Last and Penrose19, Proposition 2.10]. To the best of our knowledge, this is the first time the distance
![]() $d_\pi$
has been defined and employed in Poisson process approximation. We believe that it is possible to extend
$d_\pi$
has been defined and employed in Poisson process approximation. We believe that it is possible to extend
![]() $d_\pi$
to larger classes of point processes by restricting
$d_\pi$
to larger classes of point processes by restricting
![]() $\mathcal X^d_{\textrm{disj}}$
to suitable families of sets. For example, for locally finite point processes on a locally compact second-countable Hausdorff space (lcscH), we may define the distance
$\mathcal X^d_{\textrm{disj}}$
to suitable families of sets. For example, for locally finite point processes on a locally compact second-countable Hausdorff space (lcscH), we may define the distance
![]() $d_\pi$
by replacing
$d_\pi$
by replacing
![]() $\mathcal X^d_{\textrm{disj}}$
with the family of d-tuples of disjoint and relatively compact Borel sets. However, this falls outside the scope of this paper, and it will be treated elsewhere. Let us now state our main theoretical result on Poisson process approximation.
$\mathcal X^d_{\textrm{disj}}$
with the family of d-tuples of disjoint and relatively compact Borel sets. However, this falls outside the scope of this paper, and it will be treated elsewhere. Let us now state our main theoretical result on Poisson process approximation.
Theorem 1.2. Let
![]() $\xi$
be a point process on
$\xi$
be a point process on
![]() $\mathbb X$
with finite intensity measure, and let
$\mathbb X$
with finite intensity measure, and let
![]() $\eta$
be a Poisson process on
$\eta$
be a Poisson process on
![]() $\mathbb X$
with finite intensity measure
$\mathbb X$
with finite intensity measure
![]() $\lambda$
. For any i-tuple
$\lambda$
. For any i-tuple
![]() $(A_1,\dots,A_i)\in \mathcal X^{i}_\textrm{disj}$
with
$(A_1,\dots,A_i)\in \mathcal X^{i}_\textrm{disj}$
with
![]() $i\in\mathbb N$
, consider a random vector
$i\in\mathbb N$
, consider a random vector
![]() $\textbf{Z}^{A_{1:i}}= \left(Z^{A_{1:i}}_1,\dots,Z^{A_{1:i}}_i\right)$
defined on the same probability space as
$\textbf{Z}^{A_{1:i}}= \left(Z^{A_{1:i}}_1,\dots,Z^{A_{1:i}}_i\right)$
defined on the same probability space as
![]() $\xi$
with values in
$\xi$
with values in
![]() $\mathbb Z^i$
, and define
$\mathbb Z^i$
, and define
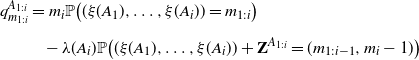 \begin{equation} \begin{split} &q^{A_{1:i}}_{m_{1:i}}=m_i \mathbb P\big((\xi(A_1),\dots ,\xi (A_i)) = m_{1:i}\big) \\[5pt] &\qquad\quad \!\!-\lambda(A_i)\mathbb{P}\big((\xi(A_1),\dots ,\xi (A_i)) + \textbf{Z}^{A_{1:i}} =(m_{1:i-1}, m_i-1)\big) \end{split} \end{equation}
\begin{equation} \begin{split} &q^{A_{1:i}}_{m_{1:i}}=m_i \mathbb P\big((\xi(A_1),\dots ,\xi (A_i)) = m_{1:i}\big) \\[5pt] &\qquad\quad \!\!-\lambda(A_i)\mathbb{P}\big((\xi(A_1),\dots ,\xi (A_i)) + \textbf{Z}^{A_{1:i}} =(m_{1:i-1}, m_i-1)\big) \end{split} \end{equation}
for
![]() $m_{1:i}\in\mathbb N_0^i$
with
$m_{1:i}\in\mathbb N_0^i$
with
![]() $m_i\neq0$
. Then
$m_i\neq0$
. Then
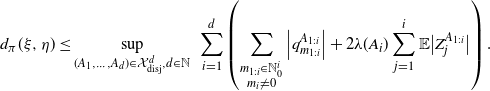 \begin{equation} d_{\pi}(\xi, \eta)\leq\sup_{(A_1,\dots , A_d)\in\mathcal X^d_{\textrm{disj}},d\in\mathbb N}\,\, \sum_{i=1}^d \left( \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}\left|q^{A_{1:i}}_{m_{1:i}}\right| + 2\lambda(A_i) \sum_{j=1}^i \mathbb E\big| Z^{A_{1:i}}_{j} \big| \right). \end{equation}
\begin{equation} d_{\pi}(\xi, \eta)\leq\sup_{(A_1,\dots , A_d)\in\mathcal X^d_{\textrm{disj}},d\in\mathbb N}\,\, \sum_{i=1}^d \left( \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}\left|q^{A_{1:i}}_{m_{1:i}}\right| + 2\lambda(A_i) \sum_{j=1}^i \mathbb E\big| Z^{A_{1:i}}_{j} \big| \right). \end{equation}
Note that a bound slightly sharper than (1.8) can be derived, as expressed in Remark 2.2.
The Poisson process approximation has mostly been studied in terms of the total variation distance in the literature; see e.g. [Reference Arratia, Goldstein and Gordon2, Reference Barbour3, Reference Barbour and Brown5, Reference Brown and Xia8, Reference Chen and Xia9, Reference Schuhmacher30, Reference Schuhmacher and Stucki31] and references therein. In contrast, [Reference Decreusefond, Schulte and Thäle10, Reference Decreusefond and Vasseur11] deal with Poisson process approximation using the Kantorovich–Rubinstein distance. Recall that the total variation distance between two point processes
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
on
$\zeta$
on
![]() $\mathbb X$
is
$\mathbb X$
is
We prove that
![]() $d_\pi$
is stronger than
$d_\pi$
is stronger than
![]() $d_{TV}$
, in the sense that convergence in
$d_{TV}$
, in the sense that convergence in
![]() $d_\pi$
implies convergence in total variation distance, but not vice versa.
$d_\pi$
implies convergence in total variation distance, but not vice versa.
Proposition 1.1. Let
![]() $\xi $
and
$\xi $
and
![]() $\zeta$
be two point processes on
$\zeta$
be two point processes on
![]() $\mathbb X$
with finite intensity measure. Then
$\mathbb X$
with finite intensity measure. Then
Note that, since
![]() $d_\pi(\xi,\zeta)\geq | \mathbb{E}[\xi(\mathbb X)] - \mathbb{E}[\zeta (\mathbb X)]|$
, Example 2.2 in [Reference Decreusefond, Schulte and Thäle10] provides a sequence of point processes
$d_\pi(\xi,\zeta)\geq | \mathbb{E}[\xi(\mathbb X)] - \mathbb{E}[\zeta (\mathbb X)]|$
, Example 2.2 in [Reference Decreusefond, Schulte and Thäle10] provides a sequence of point processes
![]() $(\zeta_n)_{n\geq 1}$
that converges in total variation distance to a point process
$(\zeta_n)_{n\geq 1}$
that converges in total variation distance to a point process
![]() $\zeta$
even though
$\zeta$
even though
![]() $d_\pi(\zeta_n,\zeta)\to\infty$
as n goes to infinity.
$d_\pi(\zeta_n,\zeta)\to\infty$
as n goes to infinity.
The Kantorovich–Rubinstein distance between two point processes
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
with finite intensity measure is defined as the optimal transportation cost between their distributions, when the cost function is the total variation distance between measures; that is,
$\zeta$
with finite intensity measure is defined as the optimal transportation cost between their distributions, when the cost function is the total variation distance between measures; that is,
where
![]() $ \Sigma(\mathbb \xi,\mathbb \zeta)$
denotes the set of all pairs of point processes
$ \Sigma(\mathbb \xi,\mathbb \zeta)$
denotes the set of all pairs of point processes
![]() $\varrho_1,\varrho_2$
on
$\varrho_1,\varrho_2$
on
![]() $\mathbb X$
defined on the same probability space such that
$\mathbb X$
defined on the same probability space such that
![]() $\varrho_1$
and
$\varrho_1$
and
![]() $\varrho_2$
follow the distributions of
$\varrho_2$
follow the distributions of
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
, respectively. We prove that, under suitable assumptions on the space,
$\zeta$
, respectively. We prove that, under suitable assumptions on the space,
![]() $d_\pi$
is dominated by
$d_\pi$
is dominated by
![]() $2d_{KR}$
, while it remains an open problem whether the two distances are equivalent or not.
$2d_{KR}$
, while it remains an open problem whether the two distances are equivalent or not.
Proposition 1.2. Let
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
be two point processes with finite intensity measure on an lcscH space
$\zeta$
be two point processes with finite intensity measure on an lcscH space
![]() $\mathbb X$
with Borel
$\mathbb X$
with Borel
![]() $\sigma$
-field
$\sigma$
-field
![]() $\mathcal X$
. Then
$\mathcal X$
. Then
The factor 2 in Proposition 1.2 cannot be improved, as shown by the following simple example: let
![]() $\mathbb X=\{a,b\}$
with
$\mathbb X=\{a,b\}$
with
![]() $\mathcal X=\{\emptyset,\{a\},\{b\},\mathbb X\}$
, and let
$\mathcal X=\{\emptyset,\{a\},\{b\},\mathbb X\}$
, and let
![]() $\delta_a$
and
$\delta_a$
and
![]() $\delta_b$
be deterministic point processes corresponding to the Dirac measures centered at a and b, respectively. Since the function
$\delta_b$
be deterministic point processes corresponding to the Dirac measures centered at a and b, respectively. Since the function
![]() $g\;:\;(x_1,x_2)\mapsto x_1-x_2$
is 1-Lipschitz, it follows that
$g\;:\;(x_1,x_2)\mapsto x_1-x_2$
is 1-Lipschitz, it follows that
On the other hand,
![]() $d_{KR}$
is bounded by the expected total variation distance between the two counting measures; thus
$d_{KR}$
is bounded by the expected total variation distance between the two counting measures; thus
![]() $d_{KR}(\delta_a,\delta_b)\leq 1$
. Hence, in this case
$d_{KR}(\delta_a,\delta_b)\leq 1$
. Hence, in this case
![]() $d_\pi(\delta_a,\delta_b)=2d_{KR}(\delta_a,\delta_b)$
. It is worth mentioning that our general result, Theorem 1.2, permits the approximation of point processes by Poisson processes on any measurable space. Hence, Theorem 1.2 can be used to obtain approximation results for point processes also when the notion of weak convergence is not defined. Moreover, when
$d_\pi(\delta_a,\delta_b)=2d_{KR}(\delta_a,\delta_b)$
. It is worth mentioning that our general result, Theorem 1.2, permits the approximation of point processes by Poisson processes on any measurable space. Hence, Theorem 1.2 can be used to obtain approximation results for point processes also when the notion of weak convergence is not defined. Moreover, when
![]() $\mathbb X$
is lcscH, convergence with respect to
$\mathbb X$
is lcscH, convergence with respect to
![]() $d_\pi$
implies convergence in distribution, as easily follows from [Reference Kallenberg16, Theorem 16.16(iii)].
$d_\pi$
implies convergence in distribution, as easily follows from [Reference Kallenberg16, Theorem 16.16(iii)].
To demonstrate the versatility of our general main results, we apply them to several examples. In Subsection 3.1, we approximate the sum of Bernoulli random vectors by a Poisson random vector. By a Bernoulli random vector, we mean a random vector with values in the set composed of the canonical vectors of
![]() $\mathbb R^d$
and the null vector. This problem has mainly been studied in terms of the total variation distance and under the assumption that the Bernoulli random vectors are independent (see e.g. [Reference Roos27]). We derive an explicit approximation result in the Wasserstein distance for the more general case of m-dependent Bernoulli random vectors.
$\mathbb R^d$
and the null vector. This problem has mainly been studied in terms of the total variation distance and under the assumption that the Bernoulli random vectors are independent (see e.g. [Reference Roos27]). We derive an explicit approximation result in the Wasserstein distance for the more general case of m-dependent Bernoulli random vectors.
In Subsections 3.2 and 3.3, we apply Theorem 1.2 to obtain explicit Poisson process approximation results for point processes with Papangelou intensity and point processes of Poisson U-statistic structure. The latter are point processes that, once evaluated on a measurable set, become Poisson U-statistics. Analogous results were already proven for the Kantorovich–Rubinstein distance in [Reference Decreusefond and Vasseur11, Theorem 3.7] and [Reference Decreusefond, Schulte and Thäle10, Theorem 3.1], under the additional condition that the configuration space
![]() $\mathbb X$
is lcscH. It is interesting to note that the proof of our result for point processes with Papangelou intensity employs Theorem 1.2 with
$\mathbb X$
is lcscH. It is interesting to note that the proof of our result for point processes with Papangelou intensity employs Theorem 1.2 with
![]() $\textbf{Z}^{A_{1:i}}$
set to zero for all i, while for point processes of U-statistic structure, we find
$\textbf{Z}^{A_{1:i}}$
set to zero for all i, while for point processes of U-statistic structure, we find
![]() $\textbf{Z}^{A_{1:i}}$
such that Equation (1.7) in Theorem 1.2 is satisfied with
$\textbf{Z}^{A_{1:i}}$
such that Equation (1.7) in Theorem 1.2 is satisfied with
![]() $q^{A_{1:i}}_{m_{1:i}}\equiv 0$
for all collections of disjoint sets.
$q^{A_{1:i}}_{m_{1:i}}\equiv 0$
for all collections of disjoint sets.
The proof of Theorem 1.1 is based on the Chen–Stein method applied to each component of the random vectors and the coupling in (1.1). In the proof of Theorem 1.2 we mimic the approach used in [Reference Arratia, Goldstein and Gordon1] to prove Theorem 2, as we derive the process bound as a consequence of the d-dimensional bound.
Before we discuss the applications in Section 3, we prove our main results in the next section.
2. Proofs of the main results
Throughout this section,
![]() $\textbf{X}=(X_1,\dots, X_d)$
is an integrable random vector with values in
$\textbf{X}=(X_1,\dots, X_d)$
is an integrable random vector with values in
![]() $\mathbb N_0^d$
and
$\mathbb N_0^d$
and
![]() $\textbf{P}=(P_{1},\dots , P_d)$
is a Poisson random vector with mean
$\textbf{P}=(P_{1},\dots , P_d)$
is a Poisson random vector with mean
![]() $\mathbb E[\textbf{P}]=(\lambda_1,\dots,\lambda_d)\in [0,\infty)^d$
. Without loss of generality we assume that
$\mathbb E[\textbf{P}]=(\lambda_1,\dots,\lambda_d)\in [0,\infty)^d$
. Without loss of generality we assume that
![]() $\textbf{X}$
and
$\textbf{X}$
and
![]() $\textbf{P}$
are independent and defined on the same probability space
$\textbf{P}$
are independent and defined on the same probability space
![]() $(\Omega,\mathfrak F,\mathbb P)$
. We denote by
$(\Omega,\mathfrak F,\mathbb P)$
. We denote by
![]() $\textrm{Lip}^d(1)$
the collection of Lipschitz functions
$\textrm{Lip}^d(1)$
the collection of Lipschitz functions
![]() $g\;:\;\mathbb N_0^d\to\mathbb R$
with respect to the metric induced by the 1-norm and Lipschitz constant bounded by 1, that is,
$g\;:\;\mathbb N_0^d\to\mathbb R$
with respect to the metric induced by the 1-norm and Lipschitz constant bounded by 1, that is,
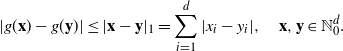 \begin{equation*} |g(\textbf{x})-g(\textbf{y})|\leq|\textbf{x}-\textbf{y}|_1=\sum_{i=1}^d |x_{i}-y_{i}|,\quad \textbf{x},\textbf{y}\in\mathbb N_0^d.\end{equation*}
\begin{equation*} |g(\textbf{x})-g(\textbf{y})|\leq|\textbf{x}-\textbf{y}|_1=\sum_{i=1}^d |x_{i}-y_{i}|,\quad \textbf{x},\textbf{y}\in\mathbb N_0^d.\end{equation*}
Clearly, this family of functions contains the 1-Lipschitz functions with respect to the Euclidean norm. For
![]() $d=1$
, we use the convention
$d=1$
, we use the convention
![]() $\textrm{Lip}(1)=\textrm{Lip}^1(1)$
.
$\textrm{Lip}(1)=\textrm{Lip}^1(1)$
.
For any fixed
![]() $g\in \textrm{Lip}(1)$
, a solution of Stein’s equation for the Poisson distribution is a real-valued function
$g\in \textrm{Lip}(1)$
, a solution of Stein’s equation for the Poisson distribution is a real-valued function
![]() $\widehat{g}^{\,(\lambda)}\;:\;\mathbb N_0\to\mathbb R$
that satisfies
$\widehat{g}^{\,(\lambda)}\;:\;\mathbb N_0\to\mathbb R$
that satisfies
where
![]() $P_\lambda$
is a Poisson random variable with mean
$P_\lambda$
is a Poisson random variable with mean
![]() $\lambda\geq 0$
. For convenience, we fix the initial condition
$\lambda\geq 0$
. For convenience, we fix the initial condition
![]() $\widehat{g}^{\,(\lambda)}(0)=0$
. With this assumption, the function
$\widehat{g}^{\,(\lambda)}(0)=0$
. With this assumption, the function
![]() $\widehat{g}^{\,(\lambda)}$
is unique and may be obtained by solving (2.1) recursively on i. An explicit expression for this solution is given in [Reference Erhardsson14, Theorem 1.2]. The following lemma is a direct consequence of [Reference Barbour and Xia7, Theorem 1.1] (note that the case
$\widehat{g}^{\,(\lambda)}$
is unique and may be obtained by solving (2.1) recursively on i. An explicit expression for this solution is given in [Reference Erhardsson14, Theorem 1.2]. The following lemma is a direct consequence of [Reference Barbour and Xia7, Theorem 1.1] (note that the case
![]() $\lambda=0$
is trivial).
$\lambda=0$
is trivial).
Lemma 2.1. For any
![]() $\lambda\geq0$
and
$\lambda\geq0$
and
![]() $g\in\textrm{Lip}(1)$
, let
$g\in\textrm{Lip}(1)$
, let
![]() $\widehat{g}^{\,(\lambda)}$
be the solution of the Stein equation (2.1) with initial condition
$\widehat{g}^{\,(\lambda)}$
be the solution of the Stein equation (2.1) with initial condition
![]() $\widehat{g}^{\,(\lambda)}(0)=0$
. Then
$\widehat{g}^{\,(\lambda)}(0)=0$
. Then
Recall that, for any
![]() $\textbf{x}=(x_1,\dots,x_d)\in\mathbb R^d$
and some index
$\textbf{x}=(x_1,\dots,x_d)\in\mathbb R^d$
and some index
![]() $1\leq j\leq d$
, we write
$1\leq j\leq d$
, we write
![]() $x_{1:j}$
and
$x_{1:j}$
and
![]() $x_{j:d}$
for the subvectors
$x_{j:d}$
for the subvectors
![]() $(x_1,\dots,x_j)$
and
$(x_1,\dots,x_j)$
and
![]() $(x_j,\dots,x_d)$
, respectively. For
$(x_j,\dots,x_d)$
, respectively. For
![]() $g\in\textrm{Lip}^d(1)$
, let
$g\in\textrm{Lip}^d(1)$
, let
![]() $\widehat{g}^{\,(\lambda)}_{x_{1:i-1}|x_{i+1:d}}$
denote the solution to (2.1) for the Lipschitz function
$\widehat{g}^{\,(\lambda)}_{x_{1:i-1}|x_{i+1:d}}$
denote the solution to (2.1) for the Lipschitz function
![]() $g(x_{1:i-1},\cdot\ ,x_{i+1:d})$
with fixed
$g(x_{1:i-1},\cdot\ ,x_{i+1:d})$
with fixed
![]() $x_{1:i-1}\in\mathbb N_0^{i-1}$
and
$x_{1:i-1}\in\mathbb N_0^{i-1}$
and
![]() $x_{i+1:d}\in\mathbb N_0^{d-i}$
. Since
$x_{i+1:d}\in\mathbb N_0^{d-i}$
. Since
![]() $\widehat{g}^{\,(\lambda)}$
takes vectors from
$\widehat{g}^{\,(\lambda)}$
takes vectors from
![]() $\mathbb N_0^d$
as input, we do not need to worry about measurability issues. The following proposition is the first building block for the proof of Theorem 1.1.
$\mathbb N_0^d$
as input, we do not need to worry about measurability issues. The following proposition is the first building block for the proof of Theorem 1.1.
Proposition 2.1. For any
![]() $g\in\textrm{Lip}^d(1)$
,
$g\in\textrm{Lip}^d(1)$
,
 \begin{equation*} \mathbb E[g(\textbf{P}) - g(\textbf{X})]=\sum_{i=1}^d\mathbb E\left[X_i\widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}|P_{i+1:d}}(X_i) -\lambda_i\widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}|P_{i+1:d}}(X_i+1)\right]. \end{equation*}
\begin{equation*} \mathbb E[g(\textbf{P}) - g(\textbf{X})]=\sum_{i=1}^d\mathbb E\left[X_i\widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}|P_{i+1:d}}(X_i) -\lambda_i\widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}|P_{i+1:d}}(X_i+1)\right]. \end{equation*}
Proof of Proposition 2.1. First, observe that
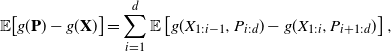 \begin{equation} \mathbb E\!\left[g(\textbf{P})-g(\textbf{X})\right] =\sum_{i=1}^d\mathbb E\left[g(X_{1:i-1},P_{i:d})-g(X_{1:i},P_{i+1:d})\right], \end{equation}
\begin{equation} \mathbb E\!\left[g(\textbf{P})-g(\textbf{X})\right] =\sum_{i=1}^d\mathbb E\left[g(X_{1:i-1},P_{i:d})-g(X_{1:i},P_{i+1:d})\right], \end{equation}
with the conventions
![]() $(X_{1:0},P_{1:d})=\textbf{P}$
and
$(X_{1:0},P_{1:d})=\textbf{P}$
and
![]() $(X_{1:d},P_{d+1:d})=\textbf{X}$
. The independence of
$(X_{1:d},P_{d+1:d})=\textbf{X}$
. The independence of
![]() $P_i$
from
$P_i$
from
![]() $P_{i+1:d}$
and
$P_{i+1:d}$
and
![]() $X_{1:i}$
implies
$X_{1:i}$
implies
where
![]() $\mathbb E^{P_i}$
denotes the expectation with respect to the random variable
$\mathbb E^{P_i}$
denotes the expectation with respect to the random variable
![]() $P_i$
. From the definition of
$P_i$
. From the definition of
![]() $\widehat{g}^{\,(\lambda_i)}_{x_{1:i-1}|x_{i+1:d}}$
with
$\widehat{g}^{\,(\lambda_i)}_{x_{1:i-1}|x_{i+1:d}}$
with
![]() $x_{1:i-1}=X_{i:i-1}$
and
$x_{1:i-1}=X_{i:i-1}$
and
![]() $x_{i+1:d}=P_{i+1:d}$
, it follows that
$x_{i+1:d}=P_{i+1:d}$
, it follows that
for all
![]() $i=1,\dots, d$
. Together with (2.3), this leads to the desired conclusion.
$i=1,\dots, d$
. Together with (2.3), this leads to the desired conclusion.
Proof of Theorem 1.1. In view of Proposition 2.1, it suffices to bound
For the remainder of the proof, the index i is fixed and we omit the superscript (i) in
![]() $Z_{1:i}^{(i)}$
. Define the function
$Z_{1:i}^{(i)}$
. Define the function
![]() $h\colon\mathbb N_0^i\to\mathbb R$
so that
$h\colon\mathbb N_0^i\to\mathbb R$
so that
where
![]() $\mathbb E[\!\cdot\! |\, Y]$
denotes the conditional expectation with respect to a random element Y. With the convention
$\mathbb E[\!\cdot\! |\, Y]$
denotes the conditional expectation with respect to a random element Y. With the convention
![]() $\widehat{g}^{\,(\lambda_i)}_{m_{1:i-1}|m_{i+1:d}}(m_i)=0$
if
$\widehat{g}^{\,(\lambda_i)}_{m_{1:i-1}|m_{i+1:d}}(m_i)=0$
if
![]() $m_{1:d}\notin\mathbb N_0^d$
, it follows from (1.1) that
$m_{1:d}\notin\mathbb N_0^d$
, it follows from (1.1) that
 \begin{align*} &\mathbb E\left[X_i \widehat{g}^{\,(\lambda_i)} _{X_{1:i-1}|P_{i+1:d}}(X_i)\right] =\mathbb E[X_i h(X_{1:i})] =\sum_{m_{1:i}\in\mathbb N_0^{i}}m_i h(m_{1:i})\mathbb P(X_{1:i}=m_{1:i}) \\[5pt] &=\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}h(m_{1:i})q_{m_{1:i}} +\lambda_i\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}h(m_{1:i}) \mathbb P\left(X_{1:i}+Z_{1:i}=(m_{1:i-1},m_{i}-1)\right) \\[5pt] &=\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}h(m_{1:i})q_{m_{1:i}} +\lambda_i\mathbb E\left[ \widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}+Z_{1:i-1}|P_{i+1:d}}(X_i+Z_i+1)\right]. \end{align*}
\begin{align*} &\mathbb E\left[X_i \widehat{g}^{\,(\lambda_i)} _{X_{1:i-1}|P_{i+1:d}}(X_i)\right] =\mathbb E[X_i h(X_{1:i})] =\sum_{m_{1:i}\in\mathbb N_0^{i}}m_i h(m_{1:i})\mathbb P(X_{1:i}=m_{1:i}) \\[5pt] &=\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}h(m_{1:i})q_{m_{1:i}} +\lambda_i\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}h(m_{1:i}) \mathbb P\left(X_{1:i}+Z_{1:i}=(m_{1:i-1},m_{i}-1)\right) \\[5pt] &=\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}h(m_{1:i})q_{m_{1:i}} +\lambda_i\mathbb E\left[ \widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}+Z_{1:i-1}|P_{i+1:d}}(X_i+Z_i+1)\right]. \end{align*}
Since
![]() $|h(X_{1:i})|\leq 1$
by (2.2), the triangle inequality establishes
$|h(X_{1:i})|\leq 1$
by (2.2), the triangle inequality establishes
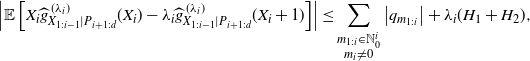 \begin{equation} \left|\mathbb E\left[X_i \widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}|P_{i+1:d}}(X_i) -\lambda_i\widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}|P_{i+1:d}}(X_i+1)\right]\right| \leq\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}\left|q_{m_{1:i}}\right|+\lambda_i(H_1+H_2), \end{equation}
\begin{equation} \left|\mathbb E\left[X_i \widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}|P_{i+1:d}}(X_i) -\lambda_i\widehat{g}^{\,(\lambda_i)}_{X_{1:i-1}|P_{i+1:d}}(X_i+1)\right]\right| \leq\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}\left|q_{m_{1:i}}\right|+\lambda_i(H_1+H_2), \end{equation}
with
and
The inequalities in (2.2) guarantee
 \begin{equation*} H_1\leq \mathbb E|Z_i| \quad\text{and}\quad H_2\leq2\mathbb P(Z_{1:i-1}\neq0)\leq\sum_{j=1}^{i-1} 2\mathbb P(Z_j\neq0)\leq 2\sum_{j=1}^{i-1} \mathbb E|Z_j|. \end{equation*}
\begin{equation*} H_1\leq \mathbb E|Z_i| \quad\text{and}\quad H_2\leq2\mathbb P(Z_{1:i-1}\neq0)\leq\sum_{j=1}^{i-1} 2\mathbb P(Z_j\neq0)\leq 2\sum_{j=1}^{i-1} \mathbb E|Z_j|. \end{equation*}
Combining (2.4) with the bounds for
![]() $H_1$
and
$H_1$
and
![]() $H_2$
and summing over
$H_2$
and summing over
![]() $i=1,\dots ,d$
concludes the proof.
$i=1,\dots ,d$
concludes the proof.
Remark 2.1. It follows directly from the previous proof that the term
![]() $\sum_{j=1}^{i-1} \mathbb E|Z_j|$
in (1.2) could be replaced by
$\sum_{j=1}^{i-1} \mathbb E|Z_j|$
in (1.2) could be replaced by
![]() $\mathbb P(Z_{1:i-1}\neq0)$
. Moreover, applying (1.4) from [Reference Barbour and Xia7, Theorem 1.1] yields
$\mathbb P(Z_{1:i-1}\neq0)$
. Moreover, applying (1.4) from [Reference Barbour and Xia7, Theorem 1.1] yields
These two observations together lead to the improved bound for Theorem 1.1:
 \begin{equation*} d_W(\textbf{X},\textbf{P})\leq\sum_{i=1}^d\left( \min\!\left\{\lambda_i,\frac{8\sqrt{\lambda_i}}{3\sqrt{2e}}\right\}\mathbb E\big|Z^{(i)}_i\big| +2\lambda_i \mathbb P\big(Z^{(i)}_{1:i-1}\neq 0\big) +\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}} \left|q_{m_{1:i}}\right|\right). \end{equation*}
\begin{equation*} d_W(\textbf{X},\textbf{P})\leq\sum_{i=1}^d\left( \min\!\left\{\lambda_i,\frac{8\sqrt{\lambda_i}}{3\sqrt{2e}}\right\}\mathbb E\big|Z^{(i)}_i\big| +2\lambda_i \mathbb P\big(Z^{(i)}_{1:i-1}\neq 0\big) +\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}} \left|q_{m_{1:i}}\right|\right). \end{equation*}
Next, we derive Theorem 1.2 from Theorem 1.1.
Proof of Theorem
1.2. Let
![]() $d\in\mathbb N$
and
$d\in\mathbb N$
and
![]() $\textbf{A}=(A_1,\dots,A_d)\in\mathcal X_\textrm{disj}^d$
. Define
$\textbf{A}=(A_1,\dots,A_d)\in\mathcal X_\textrm{disj}^d$
. Define
where
![]() $\textbf{P}^\textbf{A}$
is a Poisson random vector with mean
$\textbf{P}^\textbf{A}$
is a Poisson random vector with mean
![]() $\mathbb E[\textbf{P}^\textbf{A}]=(\lambda(A_1),\dots,\lambda(A_d))$
. By Theorem 1.1 with
$\mathbb E[\textbf{P}^\textbf{A}]=(\lambda(A_1),\dots,\lambda(A_d))$
. By Theorem 1.1 with
![]() $\textbf{Z}^{(i)}=\textbf{Z}^{A_{1:i}}$
, we obtain
$\textbf{Z}^{(i)}=\textbf{Z}^{A_{1:i}}$
, we obtain
 \begin{equation*} d_W(\textbf{X}^\textbf{A},\textbf{P}^\textbf{A})\leq\sum_{i=1}^d\left( \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}\left|q^{A_{1:i}}_{m_{1:i}}\right| +2\lambda(A_i)\sum_{j=1}^i\mathbb E|Z^{A_{1:i}}_j|\right). \end{equation*}
\begin{equation*} d_W(\textbf{X}^\textbf{A},\textbf{P}^\textbf{A})\leq\sum_{i=1}^d\left( \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}}\left|q^{A_{1:i}}_{m_{1:i}}\right| +2\lambda(A_i)\sum_{j=1}^i\mathbb E|Z^{A_{1:i}}_j|\right). \end{equation*}
Taking the supremum over all d-tuples of disjoint measurable sets concludes the proof.
Remark 2.2. By taking into account Remark 2.1, one immediately obtains
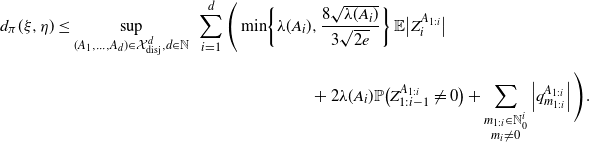 \begin{align*} d_{\pi}(\xi, \eta)&\leq\sup_{(A_1,\dots , A_d)\in\mathcal X^d_{\textrm{disj}}, d\in\mathbb N}\,\, \sum_{i=1}^d\Bigg( \min\!\left\{\lambda (A_i),\frac{8\sqrt{\lambda (A_i)}}{3\sqrt{2e}}\right\}\mathbb E\big|Z^{A_{1:i}}_i\big| \\[5pt]& \qquad \qquad \qquad \qquad \qquad \qquad \qquad +2\lambda (A_i) \mathbb P\big(Z^{A_{1:i}}_{1:i-1}\neq 0\big) +\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}} \left|q_{m_{1:i}}^{A_{1:i}}\right|\Bigg). \end{align*}
\begin{align*} d_{\pi}(\xi, \eta)&\leq\sup_{(A_1,\dots , A_d)\in\mathcal X^d_{\textrm{disj}}, d\in\mathbb N}\,\, \sum_{i=1}^d\Bigg( \min\!\left\{\lambda (A_i),\frac{8\sqrt{\lambda (A_i)}}{3\sqrt{2e}}\right\}\mathbb E\big|Z^{A_{1:i}}_i\big| \\[5pt]& \qquad \qquad \qquad \qquad \qquad \qquad \qquad +2\lambda (A_i) \mathbb P\big(Z^{A_{1:i}}_{1:i-1}\neq 0\big) +\sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}} \left|q_{m_{1:i}}^{A_{1:i}}\right|\Bigg). \end{align*}
Let us now prove that the total variation distance is dominated by
![]() $d_\pi$
. Recall that the total variation distance between two point processes
$d_\pi$
. Recall that the total variation distance between two point processes
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
on
$\zeta$
on
![]() $\mathbb X$
is
$\mathbb X$
is
The result is obtained by a monotone class theorem, [Reference Lieb and Loss21, Theorem 1.3], which is stated below as a lemma. A monotone class
![]() $\mathcal A$
is a collection of sets closed under monotone limits; that is, for any
$\mathcal A$
is a collection of sets closed under monotone limits; that is, for any
![]() $A_1,A_2,\ldots\in\mathcal A$
with
$A_1,A_2,\ldots\in\mathcal A$
with
![]() $A_n\uparrow A$
or
$A_n\uparrow A$
or
![]() $A_n\downarrow A$
, we have
$A_n\downarrow A$
, we have
![]() $A\in\mathcal A$
.
$A\in\mathcal A$
.
Lemma 2.2. Let U be a set and let
![]() $\mathcal U$
be an algebra of subsets of U. Then the monotone class generated by
$\mathcal U$
be an algebra of subsets of U. Then the monotone class generated by
![]() $\mathcal U$
coincides with the
$\mathcal U$
coincides with the
![]() $\sigma$
-field generated by
$\sigma$
-field generated by
![]() $\mathcal U$
.
$\mathcal U$
.
Proof of Proposition 1.1. Let us first introduce the set of finite counting measures
with the trace
![]() $\sigma$
-field
$\sigma$
-field
As we are dealing with finite point processes, the total variation distance is equivalently obtained if
![]() $\mathcal N_X$
is replaced by
$\mathcal N_X$
is replaced by
![]() $\mathcal N^{<\infty}_\mathbb X$
in (2.5):
$\mathcal N^{<\infty}_\mathbb X$
in (2.5):
Let
![]() $\mathcal P(\mathbb N_0^d)$
denote the power set of
$\mathcal P(\mathbb N_0^d)$
denote the power set of
![]() $\mathbb N_0^d$
, that is, the collection of all subsets of
$\mathbb N_0^d$
, that is, the collection of all subsets of
![]() $\mathbb N_0^d$
. For any
$\mathbb N_0^d$
. For any
![]() $d\in\mathbb N$
and
$d\in\mathbb N$
and
![]() $M\in\mathcal P(\mathbb N_0^d)$
note that
$M\in\mathcal P(\mathbb N_0^d)$
note that
![]() $\textbf{1}_M(\!\cdot\!)\in\textrm{Lip}^{d}(1)$
; therefore
$\textbf{1}_M(\!\cdot\!)\in\textrm{Lip}^{d}(1)$
; therefore
with
It can easily be verified that
![]() $\mathcal U$
is an algebra,
$\mathcal U$
is an algebra,
![]() $\mathcal U\subset\mathcal N^{<\infty}_\mathbb X$
, and
$\mathcal U\subset\mathcal N^{<\infty}_\mathbb X$
, and
![]() $\sigma(\mathcal U)=\mathcal N^{<\infty}_\mathbb X$
. Moreover, by (2.6),
$\sigma(\mathcal U)=\mathcal N^{<\infty}_\mathbb X$
. Moreover, by (2.6),
![]() $\mathcal U$
is a subset of the monotone class
$\mathcal U$
is a subset of the monotone class
Lemma 2.2 concludes the proof.
In the last part of this section, we show that
![]() $d_\pi$
is dominated by
$d_\pi$
is dominated by
![]() $2d_{KR}$
when the underlying space is lcscH and
$2d_{KR}$
when the underlying space is lcscH and
![]() $\mathcal X$
is the Borel
$\mathcal X$
is the Borel
![]() $\sigma$
-field. A topological space is second-countable if its topology has a countable basis, and it is locally compact if every point has an open neighborhood whose topological closure is compact. Recall that the Kantorovich–Rubinstein distance between two point processes
$\sigma$
-field. A topological space is second-countable if its topology has a countable basis, and it is locally compact if every point has an open neighborhood whose topological closure is compact. Recall that the Kantorovich–Rubinstein distance between two point processes
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
, with finite intensity measure on a measurable space
$\zeta$
, with finite intensity measure on a measurable space
![]() $\mathbb X$
, is given by
$\mathbb X$
, is given by
where
![]() $ \Sigma(\mathbb \xi,\mathbb \zeta)$
denotes the set of all pairs of point processes
$ \Sigma(\mathbb \xi,\mathbb \zeta)$
denotes the set of all pairs of point processes
![]() $\varrho_1,\varrho_2$
on
$\varrho_1,\varrho_2$
on
![]() $\mathbb X$
defined on the same probability space such that
$\mathbb X$
defined on the same probability space such that
![]() $\varrho_1$
and
$\varrho_1$
and
![]() $\varrho_2$
follow the distributions of
$\varrho_2$
follow the distributions of
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
, respectively. When the configuration space
$\zeta$
, respectively. When the configuration space
![]() $\mathbb X$
is lcscH, the Kantorovich duality theorem [Reference Villani33, Theorem 5.10] yields an equivalent definition for this metric:
$\mathbb X$
is lcscH, the Kantorovich duality theorem [Reference Villani33, Theorem 5.10] yields an equivalent definition for this metric:
where
![]() $\mathcal{L}(1)$
is the set of all measurable functions
$\mathcal{L}(1)$
is the set of all measurable functions
![]() $h\;:\;\mathsf N_\mathbb X\to \mathbb R$
that are Lipschitz continuous with respect to the total variation distance between measures,
$h\;:\;\mathsf N_\mathbb X\to \mathbb R$
that are Lipschitz continuous with respect to the total variation distance between measures,
with Lipschitz constant bounded by 1. Since
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
take values in
$\zeta$
take values in
![]() $\mathsf N_\mathbb X^{<\infty}$
, by [Reference McShane22, Theorem 1] we may assume that h is defined on
$\mathsf N_\mathbb X^{<\infty}$
, by [Reference McShane22, Theorem 1] we may assume that h is defined on
![]() $\mathsf N_\mathbb X^{<\infty}$
.
$\mathsf N_\mathbb X^{<\infty}$
.
Proof of Proposition
1.2. For
![]() $g\in\text{Lip}^d(1)$
and disjoint sets
$g\in\text{Lip}^d(1)$
and disjoint sets
![]() $A_1,\dots,A_d\in\mathcal X$
,
$A_1,\dots,A_d\in\mathcal X$
,
![]() $d\in\mathbb N,$
define
$d\in\mathbb N,$
define
![]() $h\;:\;\mathsf N_\mathbb X^{<\infty}\to\mathbb R$
by
$h\;:\;\mathsf N_\mathbb X^{<\infty}\to\mathbb R$
by
![]() $h(\nu)=g(\nu(A_1),\cdots,\nu(A_d))$
. For finite point configurations
$h(\nu)=g(\nu(A_1),\cdots,\nu(A_d))$
. For finite point configurations
![]() $\nu_1$
and
$\nu_1$
and
![]() $\nu_2$
, we obtain
$\nu_2$
, we obtain
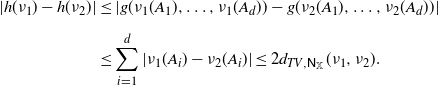 \begin{align*} |h(\nu_1)-h(\nu_2)| &\leq | g(\nu_1(A_1),\dots,\nu_1(A_d)) - g(\nu_2(A_1),\dots,\nu_2(A_d)) | \\[5pt] &\leq \sum_{i=1}^d |\nu_1(A_i)-\nu_2(A_i)| \leq 2 d_{TV,\mathsf N_\mathbb X}(\nu_1,\nu_2). \end{align*}
\begin{align*} |h(\nu_1)-h(\nu_2)| &\leq | g(\nu_1(A_1),\dots,\nu_1(A_d)) - g(\nu_2(A_1),\dots,\nu_2(A_d)) | \\[5pt] &\leq \sum_{i=1}^d |\nu_1(A_i)-\nu_2(A_i)| \leq 2 d_{TV,\mathsf N_\mathbb X}(\nu_1,\nu_2). \end{align*}
Therefore, we have
![]() $h/2\in\mathcal{L}(1)$
. Together with (2.7), this implies
$h/2\in\mathcal{L}(1)$
. Together with (2.7), this implies
![]() $|\mathbb{E}[h(\xi)]-\mathbb{E}[h(\zeta)] |\leq 2d_{KR}(\xi, \zeta)$
and concludes the proof.
$|\mathbb{E}[h(\xi)]-\mathbb{E}[h(\zeta)] |\leq 2d_{KR}(\xi, \zeta)$
and concludes the proof.
3. Applications
3.1. Sum of m-dependent Bernoulli random vectors
In this subsection, we consider a finite family of Bernoulli random vectors
![]() $\textbf{Y}^{(1)},\dots, \textbf{Y}^{(n)}$
and investigate the multivariate Poisson approximation of
$\textbf{Y}^{(1)},\dots, \textbf{Y}^{(n)}$
and investigate the multivariate Poisson approximation of
![]() $\textbf{X}=\sum_{r=1}^n \textbf{Y}^{(r)}$
in the Wasserstein distance. The distributions of
$\textbf{X}=\sum_{r=1}^n \textbf{Y}^{(r)}$
in the Wasserstein distance. The distributions of
![]() $\textbf{Y}^{(1)},\dots, \textbf{Y}^{(n)}$
are given by
$\textbf{Y}^{(1)},\dots, \textbf{Y}^{(n)}$
are given by
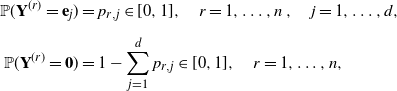 \begin{equation}\begin{aligned} \mathbb P(\textbf{Y}^{(r)}=\textbf{e}_j)&=p_{r,j}\in[0,1],\quad r=1,\dots,n\,,\quad j = 1,\dots,d,\\[5pt] \mathbb P(\textbf{Y}^{(r)}=\textbf{0})&=1-\sum_{j=1}^d p_{r,j}\in[0,1],\quad r=1,\dots,n,\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \mathbb P(\textbf{Y}^{(r)}=\textbf{e}_j)&=p_{r,j}\in[0,1],\quad r=1,\dots,n\,,\quad j = 1,\dots,d,\\[5pt] \mathbb P(\textbf{Y}^{(r)}=\textbf{0})&=1-\sum_{j=1}^d p_{r,j}\in[0,1],\quad r=1,\dots,n,\end{aligned}\end{equation}
where
![]() $\textbf{e}_j$
denotes the vector with entry 1 at position j and entry 0 otherwise. If the Bernoulli random vectors are independent and identically distributed (i.i.d.),
$\textbf{e}_j$
denotes the vector with entry 1 at position j and entry 0 otherwise. If the Bernoulli random vectors are independent and identically distributed (i.i.d.),
![]() $\textbf{X}$
has the so-called multinomial distribution. The multivariate Poisson approximation of the multinomial distribution, and more generally of the sum of independent Bernoulli random vectors, has already been tackled by many authors in terms of the total variation distance. Among others, we refer the reader to [Reference Barbour4, Reference Deheuvels and Pfeifer12, Reference Roos27, Reference Roos29] and the survey [Reference Novak23]. Unlike the abovementioned papers, we assume that
$\textbf{X}$
has the so-called multinomial distribution. The multivariate Poisson approximation of the multinomial distribution, and more generally of the sum of independent Bernoulli random vectors, has already been tackled by many authors in terms of the total variation distance. Among others, we refer the reader to [Reference Barbour4, Reference Deheuvels and Pfeifer12, Reference Roos27, Reference Roos29] and the survey [Reference Novak23]. Unlike the abovementioned papers, we assume that
![]() $\textbf{Y}^{(1)},\dots, \textbf{Y}^{(n)}$
are m-dependent. Note that the case of sums of 1-dependent random vectors has recently been treated in [Reference Čekanavičius and Vellaisamy13] using metrics that are weaker than the total variation distance. To the best of our knowledge, this is the first paper where the Poisson approximation of the sum of m-dependent Bernoulli random vectors is investigated in terms of the Wasserstein distance.
$\textbf{Y}^{(1)},\dots, \textbf{Y}^{(n)}$
are m-dependent. Note that the case of sums of 1-dependent random vectors has recently been treated in [Reference Čekanavičius and Vellaisamy13] using metrics that are weaker than the total variation distance. To the best of our knowledge, this is the first paper where the Poisson approximation of the sum of m-dependent Bernoulli random vectors is investigated in terms of the Wasserstein distance.
More precisely, for
![]() $n\in\mathbb N$
, let
$n\in\mathbb N$
, let
![]() $\textbf{Y}^{(1)},\dots,\textbf{Y}^{(n)}$
be Bernoulli random vectors with distributions given by (3.1), and assume that for a given fixed
$\textbf{Y}^{(1)},\dots,\textbf{Y}^{(n)}$
be Bernoulli random vectors with distributions given by (3.1), and assume that for a given fixed
![]() $m\in\mathbb N_0$
and any two subsets S and T of
$m\in\mathbb N_0$
and any two subsets S and T of
![]() $\{1,\dots,n\}$
such that
$\{1,\dots,n\}$
such that
![]() $\min\!(S)-\max\!(T)>m$
, the collections
$\min\!(S)-\max\!(T)>m$
, the collections
![]() $\left(\textbf{Y}^{(s)}\right)_{s\in S}$
and
$\left(\textbf{Y}^{(s)}\right)_{s\in S}$
and
![]() $\left(\textbf{Y}^{(t)}\right)_{t\in T}$
are independent. Define the random vector
$\left(\textbf{Y}^{(t)}\right)_{t\in T}$
are independent. Define the random vector
![]() $\textbf{X}=(X_1,\dots,X_d)$
as
$\textbf{X}=(X_1,\dots,X_d)$
as
Note that if
![]() $\textbf{Y}^{(r)}$
,
$\textbf{Y}^{(r)}$
,
![]() $r=1,\dots,n,$
are i.i.d., then
$r=1,\dots,n,$
are i.i.d., then
![]() $m=0$
and
$m=0$
and
![]() $\textbf{X}$
has the multinomial distribution. The mean vector of
$\textbf{X}$
has the multinomial distribution. The mean vector of
![]() $\textbf{X}$
is
$\textbf{X}$
is
![]() $\mathbb E[\textbf{X}]=(\lambda_1,\dots,\lambda_d)$
with
$\mathbb E[\textbf{X}]=(\lambda_1,\dots,\lambda_d)$
with
For
![]() $k=1,\dots,n$
and
$k=1,\dots,n$
and
![]() $m\geq 1$
let Q(k) be the quantity given by
$m\geq 1$
let Q(k) be the quantity given by
We now state the main result of this subsection.
Theorem 3.1. Let
![]() $\textbf{X}$
be as in (3.2), and let
$\textbf{X}$
be as in (3.2), and let
![]() $\textbf{P}=(P_1,\dots,P_d)$
be a Poisson random vector with mean
$\textbf{P}=(P_1,\dots,P_d)$
be a Poisson random vector with mean
![]() $\mathbb E[\textbf{P}]=(\lambda_1,\dots,\lambda_d)$
given by (3.3). Then
$\mathbb E[\textbf{P}]=(\lambda_1,\dots,\lambda_d)$
given by (3.3). Then
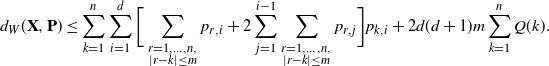 \begin{equation*} d_{W}(\textbf{X},\textbf{P}) \leq \sum_{k=1}^n \sum_{i=1}^d\bigg[ \sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{r,i} + 2\sum_{j=1}^{i-1}\sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{r,j}\bigg]p_{k,i}+ 2 d(d+1)m \sum_{k=1}^nQ(k) . \end{equation*}
\begin{equation*} d_{W}(\textbf{X},\textbf{P}) \leq \sum_{k=1}^n \sum_{i=1}^d\bigg[ \sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{r,i} + 2\sum_{j=1}^{i-1}\sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{r,j}\bigg]p_{k,i}+ 2 d(d+1)m \sum_{k=1}^nQ(k) . \end{equation*}
The proof of Theorem 3.1 is obtained by applying Theorem 1.1. When
![]() $d=1$
, Equation (1.1) corresponds to the condition required in [Reference Pianoforte and Schulte25, Theorem 1.2], which establishes sharper Poisson approximation results than the one obtained in the univariate case from Theorem 1.1. Therefore, for the sum of dependent Bernoulli random variables, a sharper bound for the Wasserstein distance can be derived from [Reference Pianoforte and Schulte25, Theorem 1.2], while for the total variation distance a bound may be deduced from [Reference Arratia, Goldstein and Gordon1, Theorem 1], [Reference Pianoforte and Schulte25, Theorem 1.2], or [Reference Smith32, Theorem 1].
$d=1$
, Equation (1.1) corresponds to the condition required in [Reference Pianoforte and Schulte25, Theorem 1.2], which establishes sharper Poisson approximation results than the one obtained in the univariate case from Theorem 1.1. Therefore, for the sum of dependent Bernoulli random variables, a sharper bound for the Wasserstein distance can be derived from [Reference Pianoforte and Schulte25, Theorem 1.2], while for the total variation distance a bound may be deduced from [Reference Arratia, Goldstein and Gordon1, Theorem 1], [Reference Pianoforte and Schulte25, Theorem 1.2], or [Reference Smith32, Theorem 1].
As a consequence of Theorem 3.1, we obtain the following result for the sum of independent Bernoulli random vectors.
Corollary 3.1. For
![]() $n\in\mathbb N$
, let
$n\in\mathbb N$
, let
![]() $\textbf{Y}^{(1)},\dots,\textbf{Y}^{(n)}$
be independent Bernoulli random vectors with distribution given by (3.1), and let
$\textbf{Y}^{(1)},\dots,\textbf{Y}^{(n)}$
be independent Bernoulli random vectors with distribution given by (3.1), and let
![]() $\textbf{X}$
be the random vector defined by (3.2). Let
$\textbf{X}$
be the random vector defined by (3.2). Let
![]() $\textbf{P}=(P_1,\dots,P_d)$
be a Poisson random vector with mean
$\textbf{P}=(P_1,\dots,P_d)$
be a Poisson random vector with mean
![]() $\mathbb E[\textbf{P}]=(\lambda_1,\dots,\lambda_d)$
given by (3.3). Then
$\mathbb E[\textbf{P}]=(\lambda_1,\dots,\lambda_d)$
given by (3.3). Then
 \begin{equation*} d_{W}(\textbf{X},\textbf{P})\leq \sum_{k=1}^n \bigg[\sum_{i=1}^d p_{k,i}\bigg]^2 . \end{equation*}
\begin{equation*} d_{W}(\textbf{X},\textbf{P})\leq \sum_{k=1}^n \bigg[\sum_{i=1}^d p_{k,i}\bigg]^2 . \end{equation*}
In [Reference Roos27, Theorem 1], a sharper bound for the total variation distance than the one obtained by Corollary 3.1 is proven. When the vectors are identically distributed and
![]() $\sum_{j=1}^d p_{1,j}\leq \alpha/n$
for some constant
$\sum_{j=1}^d p_{1,j}\leq \alpha/n$
for some constant
![]() $\alpha>0$
, our bound for the Wasserstein distance and the one in [Reference Roos27, Theorem 1] for the total variation distance differ only by a constant that does not depend on n, d, or the probabilities
$\alpha>0$
, our bound for the Wasserstein distance and the one in [Reference Roos27, Theorem 1] for the total variation distance differ only by a constant that does not depend on n, d, or the probabilities
![]() $p_{i,j}$
.
$p_{i,j}$
.
Proof of Theorem
3.1. Without loss of generality we may assume that
![]() $\lambda_1,\dots,\lambda_d>0.$
Define the random vectors
$\lambda_1,\dots,\lambda_d>0.$
Define the random vectors
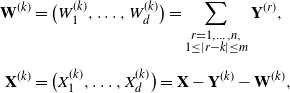 \begin{align*} \textbf{W}^{(k)} &=\big(W_1^{(k)},\dots, W_d^{(k)}\big) = \sum_{\substack{r=1,\dots, n, \\ 1\leq \vert r-k\vert \leq m} } \textbf{Y}^{(r)}, \\[5pt] \textbf{X}^{(k)} &=\big(X_1^{(k)},\dots, X_d^{(k)} \big)= \textbf{X}-\textbf{Y}^{(k)} - \textbf{W}^{(k)} , \end{align*}
\begin{align*} \textbf{W}^{(k)} &=\big(W_1^{(k)},\dots, W_d^{(k)}\big) = \sum_{\substack{r=1,\dots, n, \\ 1\leq \vert r-k\vert \leq m} } \textbf{Y}^{(r)}, \\[5pt] \textbf{X}^{(k)} &=\big(X_1^{(k)},\dots, X_d^{(k)} \big)= \textbf{X}-\textbf{Y}^{(k)} - \textbf{W}^{(k)} , \end{align*}
for
![]() $k=1,\dots,n$
. Let us fix
$k=1,\dots,n$
. Let us fix
![]() $1\leq i \leq d$
and
$1\leq i \leq d$
and
![]() $\ell_{1:i}\in \mathbb N_0^{i}$
with
$\ell_{1:i}\in \mathbb N_0^{i}$
with
![]() $\ell_i\neq 0$
. From straightforward calculations it follows that
$\ell_i\neq 0$
. From straightforward calculations it follows that
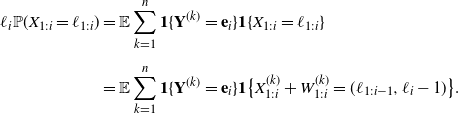 \begin{align} \ell_i\mathbb P(X_{1:i}=\ell_{1:i})&=\mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\{X_{1:i}=\ell_{1:i}\} \\[5pt] &=\mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\} \textbf{1}\big\{X^{(k)}_{1:i}+ W^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\} . \nonumber \end{align}
\begin{align} \ell_i\mathbb P(X_{1:i}=\ell_{1:i})&=\mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\{X_{1:i}=\ell_{1:i}\} \\[5pt] &=\mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\} \textbf{1}\big\{X^{(k)}_{1:i}+ W^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\} . \nonumber \end{align}
Let
![]() $H_{\ell_{1:i}} $
and
$H_{\ell_{1:i}} $
and
![]() $q_{\ell_{1:i}}$
be the quantities given by
$q_{\ell_{1:i}}$
be the quantities given by
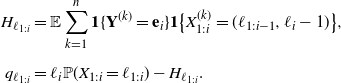 \begin{align*} H_{\ell_{1:i}} &=\mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\big\{X^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\} , \\[5pt] q_{\ell_{1:i}}&=\ell_i\mathbb P(X_{1:i}=\ell_{1:i})-H_{\ell_{1:i}}. \end{align*}
\begin{align*} H_{\ell_{1:i}} &=\mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\big\{X^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\} , \\[5pt] q_{\ell_{1:i}}&=\ell_i\mathbb P(X_{1:i}=\ell_{1:i})-H_{\ell_{1:i}}. \end{align*}
For
![]() $i=1,\dots,d$
, let
$i=1,\dots,d$
, let
![]() $\tau_i$
be a random variable independent of
$\tau_i$
be a random variable independent of
![]() $(\textbf{Y}^{(r)})_{r=1}^n$
with distribution
$(\textbf{Y}^{(r)})_{r=1}^n$
with distribution
Since
![]() $\textbf{Y}^{(r)}$
,
$\textbf{Y}^{(r)}$
,
![]() $r=1,\dots,n$
, are m-dependent, the random vectors
$r=1,\dots,n$
, are m-dependent, the random vectors
![]() $\textbf{Y}^{(k)}=\left(Y^{(k)}_1,\dots, Y^{(k)}_d \right)$
and
$\textbf{Y}^{(k)}=\left(Y^{(k)}_1,\dots, Y^{(k)}_d \right)$
and
![]() $\textbf{X}^{(k)}$
are independent for all
$\textbf{X}^{(k)}$
are independent for all
![]() $k=1,\dots,n$
. Therefore
$k=1,\dots,n$
. Therefore
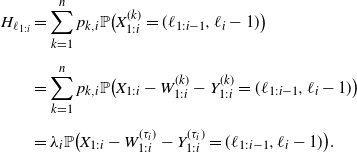 \begin{align*} H_{\ell_{1:i}} &=\sum_{k=1}^n p_{k,i}\mathbb P\big(X^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big) \\[5pt] &=\sum_{k=1}^n p_{k,i}\mathbb P\big(X_{1:i} - W^{(k)}_{1:i} - Y^{(k)}_{1:i} = ( \ell_{1:i-1},\ell_{i}-1)\big) \\[5pt] &=\lambda_i\mathbb P\big(X_{1:i}- W^{(\tau_i)}_{1:i} - Y^{(\tau_i)}_{1:i}=( \ell_{1:i-1},\ell_{i}-1)\big) . \end{align*}
\begin{align*} H_{\ell_{1:i}} &=\sum_{k=1}^n p_{k,i}\mathbb P\big(X^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big) \\[5pt] &=\sum_{k=1}^n p_{k,i}\mathbb P\big(X_{1:i} - W^{(k)}_{1:i} - Y^{(k)}_{1:i} = ( \ell_{1:i-1},\ell_{i}-1)\big) \\[5pt] &=\lambda_i\mathbb P\big(X_{1:i}- W^{(\tau_i)}_{1:i} - Y^{(\tau_i)}_{1:i}=( \ell_{1:i-1},\ell_{i}-1)\big) . \end{align*}
Then, by Theorem 1.1 we obtain
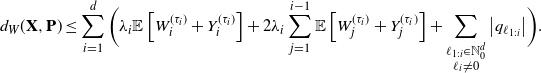 \begin{align} d_{W}(\textbf{X},\textbf{P}) \leq\sum_{i=1}^d\bigg( \lambda_i\mathbb E\left[W_i^{(\tau_i)} + Y_i^{(\tau_i)}\right] + 2\lambda_i\sum_{j=1}^{i-1}\mathbb E\left[ W_j^{(\tau_i)}+Y_j^{(\tau_i)}\right] +\sum_{\substack{\ell_{1:i}\in\mathbb N_{0}^{d}\\ \ell_i\neq 0}}\big\vert q_{\ell_{1:i}}\big\vert\bigg). \end{align}
\begin{align} d_{W}(\textbf{X},\textbf{P}) \leq\sum_{i=1}^d\bigg( \lambda_i\mathbb E\left[W_i^{(\tau_i)} + Y_i^{(\tau_i)}\right] + 2\lambda_i\sum_{j=1}^{i-1}\mathbb E\left[ W_j^{(\tau_i)}+Y_j^{(\tau_i)}\right] +\sum_{\substack{\ell_{1:i}\in\mathbb N_{0}^{d}\\ \ell_i\neq 0}}\big\vert q_{\ell_{1:i}}\big\vert\bigg). \end{align}
From (3.4) and the definition of
![]() $q_{\ell_{1:i}}$
it follows that
$q_{\ell_{1:i}}$
it follows that
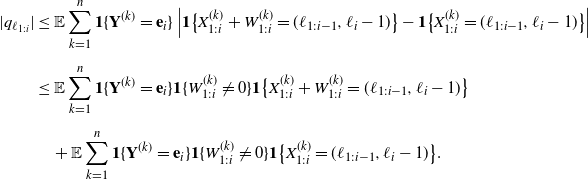 \begin{align*} | q_{\ell_{1:i}}| &\leq\mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\} \left|\textbf{1}\big\{X^{(k)}_{1:i}+ W^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\} -\textbf{1}\big\{X^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\}\right| \\[5pt] & \leq \mathbb E\sum_{k=1}^n \textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\{W_{1:i}^{(k)}\neq 0\} \textbf{1}\big\{X^{(k)}_{1:i}+ W^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\} \\[5pt] &\quad + \mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\{W_{1:i}^{(k)}\neq 0\}\textbf{1}\big\{X^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\}. \end{align*}
\begin{align*} | q_{\ell_{1:i}}| &\leq\mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\} \left|\textbf{1}\big\{X^{(k)}_{1:i}+ W^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\} -\textbf{1}\big\{X^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\}\right| \\[5pt] & \leq \mathbb E\sum_{k=1}^n \textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\{W_{1:i}^{(k)}\neq 0\} \textbf{1}\big\{X^{(k)}_{1:i}+ W^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\} \\[5pt] &\quad + \mathbb E\sum_{k=1}^n\textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\{W_{1:i}^{(k)}\neq 0\}\textbf{1}\big\{X^{(k)}_{1:i}=(\ell_{1:i-1},\ell_{i}-1)\big\}. \end{align*}
Thus, by the inequality
![]() $\textbf{1}\{W_{1:i}^{(k)}\neq 0\}\leq \sum_{j=1}^i W_j^{(k)}$
we obtain
$\textbf{1}\{W_{1:i}^{(k)}\neq 0\}\leq \sum_{j=1}^i W_j^{(k)}$
we obtain
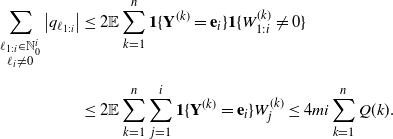 \begin{equation} \begin{split} \sum_{\substack{\ell_{1:i}\in\mathbb N_0^{i}\\ \ell_i\neq0}} \big\vert q_{\ell_{1:i}}\big\vert & \leq 2 \mathbb E\sum_{k=1}^n \textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\{W_{1:i}^{(k)}\neq 0\} \\[5pt] & \leq 2 \mathbb E\sum_{k=1}^n \sum_{j=1}^i \textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\} W_j^{(k)}\leq 4m i\sum_{k=1}^n Q(k). \end{split} \end{equation}
\begin{equation} \begin{split} \sum_{\substack{\ell_{1:i}\in\mathbb N_0^{i}\\ \ell_i\neq0}} \big\vert q_{\ell_{1:i}}\big\vert & \leq 2 \mathbb E\sum_{k=1}^n \textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\}\textbf{1}\{W_{1:i}^{(k)}\neq 0\} \\[5pt] & \leq 2 \mathbb E\sum_{k=1}^n \sum_{j=1}^i \textbf{1}\{\textbf{Y}^{(k)}=\textbf{e}_i\} W_j^{(k)}\leq 4m i\sum_{k=1}^n Q(k). \end{split} \end{equation}
Moreover, for any
![]() $i,j=1,\dots, d$
we have
$i,j=1,\dots, d$
we have
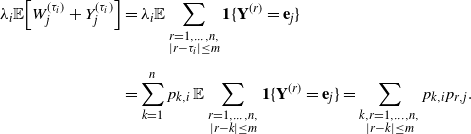 \begin{align*} \lambda_i\mathbb E \Big[W^{(\tau_i)}_j + Y^{(\tau_i)}_j \Big] &=\lambda_i\mathbb E \sum_{\substack{r=1,\dots, n, \\ \vert r-\tau_i\vert \leq m}}\textbf{1}\{\textbf{Y}^{(r)}=\textbf{e}_j\} \\[5pt] &= \sum_{k=1}^n p_{k,i}\,\mathbb E \sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}}\textbf{1}\{\textbf{Y}^{(r)}=\textbf{e}_j\} =\sum_{\substack{k,r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{k,i}p_{r,j}. \end{align*}
\begin{align*} \lambda_i\mathbb E \Big[W^{(\tau_i)}_j + Y^{(\tau_i)}_j \Big] &=\lambda_i\mathbb E \sum_{\substack{r=1,\dots, n, \\ \vert r-\tau_i\vert \leq m}}\textbf{1}\{\textbf{Y}^{(r)}=\textbf{e}_j\} \\[5pt] &= \sum_{k=1}^n p_{k,i}\,\mathbb E \sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}}\textbf{1}\{\textbf{Y}^{(r)}=\textbf{e}_j\} =\sum_{\substack{k,r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{k,i}p_{r,j}. \end{align*}
Together with (3.5) and (3.6), this leads to
 \begin{align*} d_{W}(\textbf{X},\textbf{P}) &\leq \sum_{i=1}^d\sum_{\substack{k,r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{k,i}p_{r,i} +2\sum_{i=1}^d\sum_{j=1}^{i-1}\sum_{\substack{k,r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{k,i}p_{r,j} + 2d(d+1)m \sum_{k=1}^nQ(k) \\[5pt] &= \sum_{k=1}^n \sum_{i=1}^d\bigg[ \sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{r,i} + 2\sum_{j=1}^{i-1}\sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{r,j}\bigg]p_{k,i}+ 2d(d+1)m \sum_{k=1}^nQ(k), \end{align*}
\begin{align*} d_{W}(\textbf{X},\textbf{P}) &\leq \sum_{i=1}^d\sum_{\substack{k,r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{k,i}p_{r,i} +2\sum_{i=1}^d\sum_{j=1}^{i-1}\sum_{\substack{k,r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{k,i}p_{r,j} + 2d(d+1)m \sum_{k=1}^nQ(k) \\[5pt] &= \sum_{k=1}^n \sum_{i=1}^d\bigg[ \sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{r,i} + 2\sum_{j=1}^{i-1}\sum_{\substack{r=1,\dots, n, \\ \vert r-k\vert \leq m}} p_{r,j}\bigg]p_{k,i}+ 2d(d+1)m \sum_{k=1}^nQ(k), \end{align*}
which completes the proof.
3.2. Point processes with Papangelou intensity
Let
![]() $\xi$
be a proper point process on a measurable space
$\xi$
be a proper point process on a measurable space
![]() $(\mathbb X,\mathcal X)$
, that is, a point process that can be written as
$(\mathbb X,\mathcal X)$
, that is, a point process that can be written as
![]() $\xi=\delta_{X_1}+\dots+\delta_{X_\tau}$
, for some random elements
$\xi=\delta_{X_1}+\dots+\delta_{X_\tau}$
, for some random elements
![]() $X_1,X_2,\dots$
in
$X_1,X_2,\dots$
in
![]() $\mathbb X$
and a random variable
$\mathbb X$
and a random variable
![]() $\tau\in\mathbb N_0\cup\{\infty\}$
. Note that any Poisson process can be seen as a proper point process, and that all locally finite point processes are proper if
$\tau\in\mathbb N_0\cup\{\infty\}$
. Note that any Poisson process can be seen as a proper point process, and that all locally finite point processes are proper if
![]() $(\mathbb X,\mathcal X)$
is a Borel space; see e.g. [Reference Last and Penrose19, Corollaries 3.7 and 6.5]. The so-called reduced Campbell measure
$(\mathbb X,\mathcal X)$
is a Borel space; see e.g. [Reference Last and Penrose19, Corollaries 3.7 and 6.5]. The so-called reduced Campbell measure
![]() $\mathcal C$
of
$\mathcal C$
of
![]() $\xi$
is defined on the product space
$\xi$
is defined on the product space
![]() $(\mathbb X\times\mathsf N_\mathbb X,\mathcal X\otimes\mathcal N_\mathbb X)$
by
$(\mathbb X\times\mathsf N_\mathbb X,\mathcal X\otimes\mathcal N_\mathbb X)$
by
where
![]() $\xi\setminus x$
denotes the point process
$\xi\setminus x$
denotes the point process
![]() $\xi-\delta_x$
if
$\xi-\delta_x$
if
![]() $x\in\xi$
, and
$x\in\xi$
, and
![]() $\xi$
otherwise. Let
$\xi$
otherwise. Let
![]() $\nu$
be a
$\nu$
be a
![]() $\sigma$
-finite measure on
$\sigma$
-finite measure on
![]() $(\mathbb X,\mathcal X)$
and let
$(\mathbb X,\mathcal X)$
and let
![]() $\mathbb P_\xi$
be the distribution of
$\mathbb P_\xi$
be the distribution of
![]() $\xi$
on
$\xi$
on
![]() $(\mathsf N_\mathbb X,\mathcal N_\mathbb X)$
. If
$(\mathsf N_\mathbb X,\mathcal N_\mathbb X)$
. If
![]() $\mathcal C$
is absolutely continuous with respect to
$\mathcal C$
is absolutely continuous with respect to
![]() $\nu\otimes\mathbb P_{\xi}$
, any density c of
$\nu\otimes\mathbb P_{\xi}$
, any density c of
![]() $\mathcal C$
with respect to
$\mathcal C$
with respect to
![]() $\nu\otimes\mathbb P_{\xi}$
is called (a version of) the Papangelou intensity of
$\nu\otimes\mathbb P_{\xi}$
is called (a version of) the Papangelou intensity of
![]() $\xi$
. This notion was originally introduced by Papangelou in [Reference Papangelou24]. In other words, c is a Papangelou intensity of
$\xi$
. This notion was originally introduced by Papangelou in [Reference Papangelou24]. In other words, c is a Papangelou intensity of
![]() $\xi$
relative to the measure
$\xi$
relative to the measure
![]() $\nu$
if the Georgii–Nguyen–Zessin equation
$\nu$
if the Georgii–Nguyen–Zessin equation
is satisfied for all measurable functions
![]() $u\;:\;\mathbb X\times\mathsf N_\mathbb X\rightarrow[0,\infty)$
. Intuitively,
$u\;:\;\mathbb X\times\mathsf N_\mathbb X\rightarrow[0,\infty)$
. Intuitively,
![]() $c(x,\xi)$
is a random variable that measures the interaction between x and
$c(x,\xi)$
is a random variable that measures the interaction between x and
![]() $\xi$
; as a reinforcement of this idea, it is well known that if c is deterministic, that is,
$\xi$
; as a reinforcement of this idea, it is well known that if c is deterministic, that is,
![]() $c(x,\xi)=f(x)$
for some positive and measurable function f, then
$c(x,\xi)=f(x)$
for some positive and measurable function f, then
![]() $\xi$
is a Poisson process with intensity measure
$\xi$
is a Poisson process with intensity measure
![]() $\lambda (A)=\int_{A}f(x)\nu(dx)$
,
$\lambda (A)=\int_{A}f(x)\nu(dx)$
,
![]() $A\in \mathcal X$
; see e.g. [Reference Last and Penrose19, Theorem 4.1]. For more details on this interpretation we refer the reader to [Reference Decreusefond and Vasseur11, Section 4]; see also [Reference Last and Otto18] and [Reference Schuhmacher and Stucki31] for connections between the Papangelou intensity and Gibbs point processes.
$A\in \mathcal X$
; see e.g. [Reference Last and Penrose19, Theorem 4.1]. For more details on this interpretation we refer the reader to [Reference Decreusefond and Vasseur11, Section 4]; see also [Reference Last and Otto18] and [Reference Schuhmacher and Stucki31] for connections between the Papangelou intensity and Gibbs point processes.
In the next theorem we prove a bound for the
![]() $d_\pi$
distance between a point process
$d_\pi$
distance between a point process
![]() $\xi$
that admits Papangelou intensity relative to a measure
$\xi$
that admits Papangelou intensity relative to a measure
![]() $\nu$
, and a Poisson process
$\nu$
, and a Poisson process
![]() $\eta$
with intensity measure
$\eta$
with intensity measure
![]() $\lambda$
absolutely continuous with respect to
$\lambda$
absolutely continuous with respect to
![]() $\nu$
. For a locally compact metric space, Theorem 3.2 yields the same bound as [Reference Decreusefond and Vasseur11, Theorem 3.7], but for the metric
$\nu$
. For a locally compact metric space, Theorem 3.2 yields the same bound as [Reference Decreusefond and Vasseur11, Theorem 3.7], but for the metric
![]() $d_\pi$
instead of the Kantorovich–Rubinstein distance.
$d_\pi$
instead of the Kantorovich–Rubinstein distance.
Theorem 3.2. Let
![]() $\xi$
be a proper point process on
$\xi$
be a proper point process on
![]() $\mathbb X$
that admits Papangelou intensity c with respect to a
$\mathbb X$
that admits Papangelou intensity c with respect to a
![]() $\sigma$
-finite measure
$\sigma$
-finite measure
![]() $\nu$
such that
$\nu$
such that
![]() $\int_\mathbb X\mathbb E|c(x,\xi)|\nu(dx)<\infty$
. Let
$\int_\mathbb X\mathbb E|c(x,\xi)|\nu(dx)<\infty$
. Let
![]() $\eta$
be a Poisson process on
$\eta$
be a Poisson process on
![]() $\mathbb X$
with finite intensity measure
$\mathbb X$
with finite intensity measure
![]() $\lambda$
having density f with respect to
$\lambda$
having density f with respect to
![]() $\nu$
. Then
$\nu$
. Then
Proof of Theorem
3.2. The condition
![]() $\int_\mathbb X\mathbb E|c(x,\xi)|\nu(dx)<\infty$
and Equation (3.7) ensure that
$\int_\mathbb X\mathbb E|c(x,\xi)|\nu(dx)<\infty$
and Equation (3.7) ensure that
![]() $\xi$
has finite intensity measure. Consider
$\xi$
has finite intensity measure. Consider
![]() $i\in\mathbb N$
and
$i\in\mathbb N$
and
![]() $(A_1,\dots,A_i)\in\mathcal X_\textrm{disj}^i$
. Hereafter,
$(A_1,\dots,A_i)\in\mathcal X_\textrm{disj}^i$
. Hereafter,
![]() $\xi(A_{1:i})$
is shorthand notation for
$\xi(A_{1:i})$
is shorthand notation for
![]() $(\xi(A_1),\dots,\xi(A_i))$
. The idea of the proof is to apply Theorem 1.2 with the random vectors
$(\xi(A_1),\dots,\xi(A_i))$
. The idea of the proof is to apply Theorem 1.2 with the random vectors
![]() $\textbf{Z}^{A_{1:i}}$
assumed to be
$\textbf{Z}^{A_{1:i}}$
assumed to be
![]() $\textbf{0}$
. In this case,
$\textbf{0}$
. In this case,
 \begin{align*} q^{A_{1:i}}_{m_{1:i}} &=m_i\mathbb P\big(\xi(A_{1:i})=m_{1:i}\big)-\lambda(A_i) \mathbb P\big(\xi(A_{1:i})=(m_{1:i-1},m_i-1)\big) \\[5pt] &=m_i\mathbb P\big(\xi(A_{1:i})=m_{1:i}\big) -\int_\mathbb X\mathbb E\big[f(x)\textbf{1}_{A_i}(x) \textbf{1}\{\xi(A_{1:i})=(m_{1:i-1},m_i-1)\}\big] \nu(dx) \end{align*}
\begin{align*} q^{A_{1:i}}_{m_{1:i}} &=m_i\mathbb P\big(\xi(A_{1:i})=m_{1:i}\big)-\lambda(A_i) \mathbb P\big(\xi(A_{1:i})=(m_{1:i-1},m_i-1)\big) \\[5pt] &=m_i\mathbb P\big(\xi(A_{1:i})=m_{1:i}\big) -\int_\mathbb X\mathbb E\big[f(x)\textbf{1}_{A_i}(x) \textbf{1}\{\xi(A_{1:i})=(m_{1:i-1},m_i-1)\}\big] \nu(dx) \end{align*}
for
![]() $m_{1:i}\in\mathbb N_0^i$
with
$m_{1:i}\in\mathbb N_0^i$
with
![]() $m_i\neq 0$
,
$m_i\neq 0$
,
![]() $i=1,\dots,d$
. It follows from (3.7) that
$i=1,\dots,d$
. It follows from (3.7) that
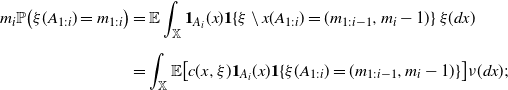 \begin{align*} m_i\mathbb P\big(\xi(A_{1:i})=m_{1:i}\big) &=\mathbb E\int_\mathbb X\textbf{1}_{A_i}(x)\textbf{1}\{\xi\setminus x(A_{1:i})=(m_{1:i-1}, m_i -1)\}\,\xi(dx) \\[5pt] &=\int_\mathbb X\mathbb E\big[c(x,\xi)\textbf{1}_{A_i}(x) \textbf{1}\{\xi(A_{1:i})=(m_{1:i-1},m_i -1)\}\big]\nu(dx); \end{align*}
\begin{align*} m_i\mathbb P\big(\xi(A_{1:i})=m_{1:i}\big) &=\mathbb E\int_\mathbb X\textbf{1}_{A_i}(x)\textbf{1}\{\xi\setminus x(A_{1:i})=(m_{1:i-1}, m_i -1)\}\,\xi(dx) \\[5pt] &=\int_\mathbb X\mathbb E\big[c(x,\xi)\textbf{1}_{A_i}(x) \textbf{1}\{\xi(A_{1:i})=(m_{1:i-1},m_i -1)\}\big]\nu(dx); \end{align*}
hence
Theorem 1.2 yields
 \begin{equation*} d_{\pi}(\xi, \eta)\leq \underset{(A_1,\dots , A_d)\in\mathcal X^d_{\textrm{disj}},d\in\mathbb N}{\sup} \,\, \sum_{i=1}^d \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}} \left|q^{A_{1:i}}_{m_{1:i}}\right| . \end{equation*}
\begin{equation*} d_{\pi}(\xi, \eta)\leq \underset{(A_1,\dots , A_d)\in\mathcal X^d_{\textrm{disj}},d\in\mathbb N}{\sup} \,\, \sum_{i=1}^d \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq0}} \left|q^{A_{1:i}}_{m_{1:i}}\right| . \end{equation*}
The inequalities
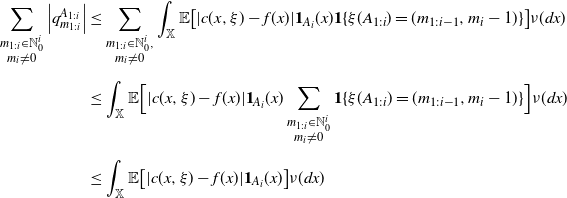 \begin{align*} \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq 0}} \left|q^{A_{1:i}}_{m_{1:i}}\right| &\leq \sum_{\substack{m_{1:i}\in\mathbb N_0^{i},\\ m_i\neq 0}} \int_\mathbb X\mathbb E\big[|c(x,\xi)-f(x)|\textbf{1}_{A_i}(x) \textbf{1}\{\xi(A_{1:i})=(m_{1:i-1},m_i -1)\}\big]\nu(dx) \\[5pt] &\leq \int_\mathbb X\mathbb E\Big[|c(x,\xi)-f(x)|\textbf{1}_{A_i}(x) \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq 0}} \textbf{1}\{\xi(A_{1:i})=(m_{1:i-1},m_i -1)\}\Big]\nu(dx) \\[5pt] &\leq\int_\mathbb X\mathbb E\big[|c(x,\xi)-f(x)|\textbf{1}_{A_i}(x)\big]\nu(dx) \end{align*}
\begin{align*} \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq 0}} \left|q^{A_{1:i}}_{m_{1:i}}\right| &\leq \sum_{\substack{m_{1:i}\in\mathbb N_0^{i},\\ m_i\neq 0}} \int_\mathbb X\mathbb E\big[|c(x,\xi)-f(x)|\textbf{1}_{A_i}(x) \textbf{1}\{\xi(A_{1:i})=(m_{1:i-1},m_i -1)\}\big]\nu(dx) \\[5pt] &\leq \int_\mathbb X\mathbb E\Big[|c(x,\xi)-f(x)|\textbf{1}_{A_i}(x) \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq 0}} \textbf{1}\{\xi(A_{1:i})=(m_{1:i-1},m_i -1)\}\Big]\nu(dx) \\[5pt] &\leq\int_\mathbb X\mathbb E\big[|c(x,\xi)-f(x)|\textbf{1}_{A_i}(x)\big]\nu(dx) \end{align*}
imply that
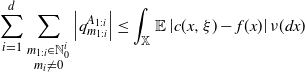 \begin{equation*} \sum_{i=1}^d \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq 0}} \left|q^{A_{1:i}}_{m_{1:i}}\right| \leq \int_\mathbb X\mathbb E\left|c(x,\xi)-f(x)\right|\nu(dx) \end{equation*}
\begin{equation*} \sum_{i=1}^d \sum_{\substack{m_{1:i}\in\mathbb N_0^{i}\\ m_i\neq 0}} \left|q^{A_{1:i}}_{m_{1:i}}\right| \leq \int_\mathbb X\mathbb E\left|c(x,\xi)-f(x)\right|\nu(dx) \end{equation*}
for any
![]() $A_{1:d}\in \mathcal X^d_{\textrm{disj}}$
with
$A_{1:d}\in \mathcal X^d_{\textrm{disj}}$
with
![]() $d\in\mathbb N$
. Thus, we obtain the assertion.
$d\in\mathbb N$
. Thus, we obtain the assertion.
3.3. Point processes of Poisson U-statistic structure
Let
![]() $(\mathbb X,\mathcal X)$
and
$(\mathbb X,\mathcal X)$
and
![]() $(\mathbb Y,\mathcal Y)$
be measurable spaces. For
$(\mathbb Y,\mathcal Y)$
be measurable spaces. For
![]() $k\in\mathbb N$
and a symmetric domain
$k\in\mathbb N$
and a symmetric domain
![]() $D\in\mathcal X^k$
, let
$D\in\mathcal X^k$
, let
![]() $g\;:\;D\to\mathbb Y$
be a symmetric measurable function; i.e., for any
$g\;:\;D\to\mathbb Y$
be a symmetric measurable function; i.e., for any
![]() $(x_1,\dots,x_k)\in D$
and index permutation
$(x_1,\dots,x_k)\in D$
and index permutation
![]() $\sigma$
,
$\sigma$
,
![]() $(x_{\sigma(1)},\dots,x_{\sigma{(k)}})\in D$
and
$(x_{\sigma(1)},\dots,x_{\sigma{(k)}})\in D$
and
![]() $g(x_1,\dots,x_k)=g(x_{\sigma(1)},\dots,x_{\sigma{(k)}})$
. Let
$g(x_1,\dots,x_k)=g(x_{\sigma(1)},\dots,x_{\sigma{(k)}})$
. Let
![]() $\eta$
be a Poisson process on
$\eta$
be a Poisson process on
![]() $\mathbb X$
with finite intensity measure
$\mathbb X$
with finite intensity measure
![]() $\mu$
. We are interested in the point process on
$\mu$
. We are interested in the point process on
![]() $\mathbb Y$
given by
$\mathbb Y$
given by
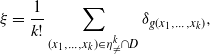 \begin{equation} \xi=\frac{1}{k!}\sum_{(x_1,\dots, x_k)\in\eta^{k}_{\neq}\cap D}\delta_{g(x_1,\dots, x_k)} ,\end{equation}
\begin{equation} \xi=\frac{1}{k!}\sum_{(x_1,\dots, x_k)\in\eta^{k}_{\neq}\cap D}\delta_{g(x_1,\dots, x_k)} ,\end{equation}
where
![]() $\eta^k_{\neq}$
denotes the collection of all k-tuples
$\eta^k_{\neq}$
denotes the collection of all k-tuples
![]() $(x_1,\dots,x_k)$
of points from
$(x_1,\dots,x_k)$
of points from
![]() $\eta$
with pairwise distinct indices. The point process
$\eta$
with pairwise distinct indices. The point process
![]() $\xi$
has a Poisson U-statistic structure in the sense that, for any
$\xi$
has a Poisson U-statistic structure in the sense that, for any
![]() $B\in\mathcal Y$
,
$B\in\mathcal Y$
,
![]() $\xi(B)$
is a Poisson U-statistic of order k. We refer to the monographs [Reference Koroljuk and Borovskich17, Reference Lee20] for more details on U-statistics and their applications to statistics. Hereafter we discuss the Poisson process approximation in the metric
$\xi(B)$
is a Poisson U-statistic of order k. We refer to the monographs [Reference Koroljuk and Borovskich17, Reference Lee20] for more details on U-statistics and their applications to statistics. Hereafter we discuss the Poisson process approximation in the metric
![]() $d_\pi$
for the point process
$d_\pi$
for the point process
![]() $\xi$
. We prove the exact analogue of [Reference Decreusefond, Schulte and Thäle10, Theorem 3.1], with the Kantorovich–Rubinstein distance replaced by
$\xi$
. We prove the exact analogue of [Reference Decreusefond, Schulte and Thäle10, Theorem 3.1], with the Kantorovich–Rubinstein distance replaced by
![]() $d_\pi$
. Several applications of this result are presented in [Reference Decreusefond, Schulte and Thäle10], alongside the case of underlying binomial point processes. It is worth mentioning that [Reference Decreusefond, Schulte and Thäle10] relies on a slightly less general setup:
$d_\pi$
. Several applications of this result are presented in [Reference Decreusefond, Schulte and Thäle10], alongside the case of underlying binomial point processes. It is worth mentioning that [Reference Decreusefond, Schulte and Thäle10] relies on a slightly less general setup:
![]() $\mathbb X$
is assumed to be an lcscH space, while in the present work any measurable space is allowed.
$\mathbb X$
is assumed to be an lcscH space, while in the present work any measurable space is allowed.
Let
![]() $\lambda$
denote the intensity measure of
$\lambda$
denote the intensity measure of
![]() $\xi$
, and note that, since
$\xi$
, and note that, since
![]() $\mu$
is a finite measure on
$\mu$
is a finite measure on
![]() $\mathbb X$
, by the multivariate Mecke formula
$\mathbb X$
, by the multivariate Mecke formula
![]() $\lambda(\mathbb Y)<\infty$
. Define
$\lambda(\mathbb Y)<\infty$
. Define
for
![]() $k\geq 2$
, and put
$k\geq 2$
, and put
![]() $R =0$
for
$R =0$
for
![]() $k=1$
.
$k=1$
.
Theorem 3.3. Let
![]() $\xi$
,
$\xi$
,
![]() $\lambda$
, and R be as above, and let
$\lambda$
, and R be as above, and let
![]() $\gamma$
be a Poisson process on
$\gamma$
be a Poisson process on
![]() $\mathbb Y$
with intensity measure
$\mathbb Y$
with intensity measure
![]() $\lambda$
. Then
$\lambda$
. Then
If the intensity measure
![]() $\lambda$
of
$\lambda$
of
![]() $\xi$
is the zero measure, then the proof of Theorem 3.3 is trivial. From now on, we assume
$\xi$
is the zero measure, then the proof of Theorem 3.3 is trivial. From now on, we assume
![]() $0<\lambda(\mathbb Y)<\infty$
. The multivariate Mecke formula yields for every
$0<\lambda(\mathbb Y)<\infty$
. The multivariate Mecke formula yields for every
![]() $A \in\mathcal Y$
that
$A \in\mathcal Y$
that
 \begin{align*} \lambda(A)=\mathbb E[\xi(A)] =\frac{1}{k!}\mathbb E\underset{\textbf{x}\in\eta^{k}_{\neq}\cap D}{\sum}\textbf{1}\{g (\textbf{x})\in A\} =\frac{1}{k!}\int_{D}\textbf{1}\{g (\textbf{x})\in A\}\,\mu^k(d\textbf{x}).\end{align*}
\begin{align*} \lambda(A)=\mathbb E[\xi(A)] =\frac{1}{k!}\mathbb E\underset{\textbf{x}\in\eta^{k}_{\neq}\cap D}{\sum}\textbf{1}\{g (\textbf{x})\in A\} =\frac{1}{k!}\int_{D}\textbf{1}\{g (\textbf{x})\in A\}\,\mu^k(d\textbf{x}).\end{align*}
Define the random element
![]() $\textbf{X}^A=(X^A_1,\dots, X^A_k)$
in
$\textbf{X}^A=(X^A_1,\dots, X^A_k)$
in
![]() $\mathbb X^k$
independent of
$\mathbb X^k$
independent of
![]() $\eta$
and distributed according to
$\eta$
and distributed according to
for all B in the product
![]() $\sigma$
-field of
$\sigma$
-field of
![]() $\mathbb X^k$
when
$\mathbb X^k$
when
![]() $\lambda(A)>0$
, and set
$\lambda(A)>0$
, and set
![]() $\textbf{X}^A=\textbf{x}_0$
for some
$\textbf{X}^A=\textbf{x}_0$
for some
![]() $\textbf{x}_0\in\mathbb X^k$
when
$\textbf{x}_0\in\mathbb X^k$
when
![]() $\lambda(A)=0$
. For any vector
$\lambda(A)=0$
. For any vector
![]() $\textbf{x}=(x_1,\dots,x_k)\in\mathbb X^k$
, denote by
$\textbf{x}=(x_1,\dots,x_k)\in\mathbb X^k$
, denote by
![]() $\Delta(\textbf{x})$
the sum of k Dirac measures located at the vector components; that is,
$\Delta(\textbf{x})$
the sum of k Dirac measures located at the vector components; that is,
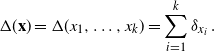 \begin{equation*} \Delta(\textbf{x})=\Delta(x_1,\dots,x_k)=\sum_{i=1}^k \delta_{x_i}\,.\end{equation*}
\begin{equation*} \Delta(\textbf{x})=\Delta(x_1,\dots,x_k)=\sum_{i=1}^k \delta_{x_i}\,.\end{equation*}
In what follows, for any point process
![]() $\zeta$
on
$\zeta$
on
![]() $\mathbb X$
,
$\mathbb X$
,
![]() $\xi(\zeta)$
is the point process defined as in (3.8) with
$\xi(\zeta)$
is the point process defined as in (3.8) with
![]() $\eta$
replaced by
$\eta$
replaced by
![]() $\zeta$
. Furthermore, as in Section 3.2,
$\zeta$
. Furthermore, as in Section 3.2,
![]() $\xi(A_{1:i})$
denotes the random vector
$\xi(A_{1:i})$
denotes the random vector
![]() $(\xi(A_1),\dots,\xi(A_i))$
, for any
$(\xi(A_1),\dots,\xi(A_i))$
, for any
![]() $A_1,\dots,A_i\in \mathcal Y$
,
$A_1,\dots,A_i\in \mathcal Y$
,
![]() $i\in\mathbb N$
.
$i\in\mathbb N$
.
Proof of Theorem
3.3. For
![]() $k=1$
, Theorem 3.3 is a direct consequence of [Reference Last and Penrose19, Theorem 5.1]. We therefore assume
$k=1$
, Theorem 3.3 is a direct consequence of [Reference Last and Penrose19, Theorem 5.1]. We therefore assume
![]() $k\geq 2$
. Let
$k\geq 2$
. Let
![]() $A_1,\dots, A_i\in\mathcal Y$
with
$A_1,\dots, A_i\in\mathcal Y$
with
![]() $i\in\mathbb N$
be disjoint sets and let
$i\in\mathbb N$
be disjoint sets and let
![]() $m_{1:i}\in\mathbb N_0^i$
with
$m_{1:i}\in\mathbb N_0^i$
with
![]() $m_i\neq 0$
. Suppose
$m_i\neq 0$
. Suppose
![]() $\lambda(A_i)>0$
. The multivariate Mecke formula implies that
$\lambda(A_i)>0$
. The multivariate Mecke formula implies that
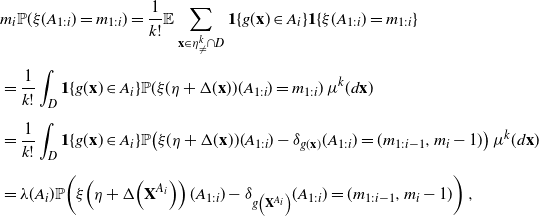 \begin{equation} \begin{split} &m_i\mathbb P(\xi(A_{1:i})=m_{1:i} ) =\frac{1}{k!}\mathbb E\sum_{\textbf{x}\in\eta^{k}_{\neq}\cap D} \textbf{1}\{g(\textbf{x})\in A_i \}\textbf{1}\{\xi(A_{1:i})=m_{1:i}\} \\[5pt] & = \frac{1}{k!}\int_{D}\textbf{1}\{g(\textbf{x})\in A_i\} \mathbb P(\xi(\eta + \Delta(\textbf{x}))(A_{1:i})=m_{1:i})\,\mu^k(d\textbf{x}) \\[5pt] & =\frac{1}{k!}\int_D\textbf{1}\{g(\textbf{x})\in A_i\} \mathbb P\!\left(\xi(\eta+\Delta(\textbf{x}))(A_{1:i})-\delta_{g(\textbf{x})}(A_{1:i}) =(m_{1:i-1},m_i -1)\right)\mu^k(d\textbf{x}) \\[5pt] & =\lambda(A_i)\mathbb P\!\left( \xi\!\left(\eta+\Delta\!\left(\textbf{X}^{A_i}\right)\right)(A_{1:i})-\delta_{g\left(\textbf{X}^{A_i}\right)} (A_{1:i})=(m_{1:i-1},m_i -1)\right), \end{split} \end{equation}
\begin{equation} \begin{split} &m_i\mathbb P(\xi(A_{1:i})=m_{1:i} ) =\frac{1}{k!}\mathbb E\sum_{\textbf{x}\in\eta^{k}_{\neq}\cap D} \textbf{1}\{g(\textbf{x})\in A_i \}\textbf{1}\{\xi(A_{1:i})=m_{1:i}\} \\[5pt] & = \frac{1}{k!}\int_{D}\textbf{1}\{g(\textbf{x})\in A_i\} \mathbb P(\xi(\eta + \Delta(\textbf{x}))(A_{1:i})=m_{1:i})\,\mu^k(d\textbf{x}) \\[5pt] & =\frac{1}{k!}\int_D\textbf{1}\{g(\textbf{x})\in A_i\} \mathbb P\!\left(\xi(\eta+\Delta(\textbf{x}))(A_{1:i})-\delta_{g(\textbf{x})}(A_{1:i}) =(m_{1:i-1},m_i -1)\right)\mu^k(d\textbf{x}) \\[5pt] & =\lambda(A_i)\mathbb P\!\left( \xi\!\left(\eta+\Delta\!\left(\textbf{X}^{A_i}\right)\right)(A_{1:i})-\delta_{g\left(\textbf{X}^{A_i}\right)} (A_{1:i})=(m_{1:i-1},m_i -1)\right), \end{split} \end{equation}
where the second-to-last equality holds true because
![]() $\delta_{g(\textbf{x})}(A_{1:i})$
is the vector
$\delta_{g(\textbf{x})}(A_{1:i})$
is the vector
![]() $(0,\dots,0,1)\in\mathbb N_0^i$
when
$(0,\dots,0,1)\in\mathbb N_0^i$
when
![]() $g(\textbf{x})\in A_i$
. The previous identity is also satisfied if
$g(\textbf{x})\in A_i$
. The previous identity is also satisfied if
![]() $\lambda(A_i)=0$
. Hence, for
$\lambda(A_i)=0$
. Hence, for
the quantity
![]() $q_{m_{1:i}}^{A_{1:i}}$
defined by Equation (1.7) in Theorem 1.2 is zero. Note that
$q_{m_{1:i}}^{A_{1:i}}$
defined by Equation (1.7) in Theorem 1.2 is zero. Note that
![]() $\textbf{Z}^{A_{1:i}}$
has nonnegative components. Hence, for any
$\textbf{Z}^{A_{1:i}}$
has nonnegative components. Hence, for any
![]() $d\in\mathbb N$
and
$d\in\mathbb N$
and
![]() $(A_1,\dots,A_d)\in\mathcal X_\textrm{disj}^{d}$
,
$(A_1,\dots,A_d)\in\mathcal X_\textrm{disj}^{d}$
,
 \begin{align*} \sum_{i=1}^d \lambda(A_i)\sum_{j=1}^i\mathbb E\left|\textbf{Z}_j^{A_{1:i}}\right| &=\sum_{i=1}^d \lambda(A_i)\sum_{j=1}^i \mathbb E\left[\xi\!\left(\eta+\Delta\left(\textbf{X}^{A_i}\right)\right)(A_j) -\xi(A_j)-\delta_{g\left(\textbf{X}^{A_i}\right)}(A_j)\right] \\[5pt] &\leq\sum_{i=1}^d \lambda(A_i) \mathbb E\left[\xi\left(\eta+\Delta\left(\textbf{X}^{A_i}\right)\right)(\mathbb Y)-\xi(\mathbb Y)-1\right] \\[5pt] &=\frac{1}{k!}\sum_{i=1}^d\int_D\textbf{1}\{g(\textbf{x})\in A_i\}\mathbb E\left[ \xi(\eta+\Delta(\textbf{x}))(\mathbb Y)-\xi(\mathbb Y)-1\right] \mu^k(d\textbf{x}) \\[5pt] &\leq \lambda(\mathbb Y)\mathbb E\left[\xi\left(\eta+\Delta\left(\textbf{X}^\mathbb Y\right)\right)(\mathbb Y)-\xi(\mathbb Y)-1\right]. \end{align*}
\begin{align*} \sum_{i=1}^d \lambda(A_i)\sum_{j=1}^i\mathbb E\left|\textbf{Z}_j^{A_{1:i}}\right| &=\sum_{i=1}^d \lambda(A_i)\sum_{j=1}^i \mathbb E\left[\xi\!\left(\eta+\Delta\left(\textbf{X}^{A_i}\right)\right)(A_j) -\xi(A_j)-\delta_{g\left(\textbf{X}^{A_i}\right)}(A_j)\right] \\[5pt] &\leq\sum_{i=1}^d \lambda(A_i) \mathbb E\left[\xi\left(\eta+\Delta\left(\textbf{X}^{A_i}\right)\right)(\mathbb Y)-\xi(\mathbb Y)-1\right] \\[5pt] &=\frac{1}{k!}\sum_{i=1}^d\int_D\textbf{1}\{g(\textbf{x})\in A_i\}\mathbb E\left[ \xi(\eta+\Delta(\textbf{x}))(\mathbb Y)-\xi(\mathbb Y)-1\right] \mu^k(d\textbf{x}) \\[5pt] &\leq \lambda(\mathbb Y)\mathbb E\left[\xi\left(\eta+\Delta\left(\textbf{X}^\mathbb Y\right)\right)(\mathbb Y)-\xi(\mathbb Y)-1\right]. \end{align*}
Thus, Theorem 1.2 gives
From (3.9) with
![]() $i=1$
and
$i=1$
and
![]() $A_1=\mathbb Y,$
it follows that the random variable
$A_1=\mathbb Y,$
it follows that the random variable
![]() $\xi\left(\eta+\Delta\left(\textbf{X}^\mathbb Y\right)\right)(\mathbb Y)$
has the size bias distribution of
$\xi\left(\eta+\Delta\left(\textbf{X}^\mathbb Y\right)\right)(\mathbb Y)$
has the size bias distribution of
![]() $\xi(\mathbb Y)$
. The property (1.6) with f being the identity function and simple algebraic computations yield
$\xi(\mathbb Y)$
. The property (1.6) with f being the identity function and simple algebraic computations yield
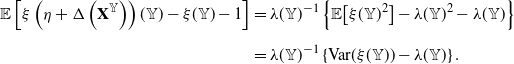 \begin{equation} \begin{split} \mathbb E\left[\xi\left(\eta+\Delta\left(\textbf{X}^\mathbb Y\right)\right)(\mathbb Y)-\xi(\mathbb Y)-1\right] &=\lambda(\mathbb Y)^{-1}\left\{\mathbb E\big[ \xi(\mathbb Y)^2\big]-\lambda(\mathbb Y)^2-\lambda(\mathbb Y)\right\} \\[5pt] &=\lambda(\mathbb Y)^{-1}\left\{\textrm{Var}(\xi(\mathbb Y))-\lambda(\mathbb Y)\right\}. \end{split} \end{equation}
\begin{equation} \begin{split} \mathbb E\left[\xi\left(\eta+\Delta\left(\textbf{X}^\mathbb Y\right)\right)(\mathbb Y)-\xi(\mathbb Y)-1\right] &=\lambda(\mathbb Y)^{-1}\left\{\mathbb E\big[ \xi(\mathbb Y)^2\big]-\lambda(\mathbb Y)^2-\lambda(\mathbb Y)\right\} \\[5pt] &=\lambda(\mathbb Y)^{-1}\left\{\textrm{Var}(\xi(\mathbb Y))-\lambda(\mathbb Y)\right\}. \end{split} \end{equation}
Moreover, [Reference Reitzner and Schulte26, Lemma 3.5] gives
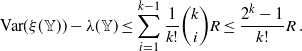 \begin{equation*} \textrm{Var}(\xi(\mathbb Y))-\lambda(\mathbb Y) \leq \sum_{i=1}^{k-1} \frac{1}{k!} \binom{k}{i} R \leq \frac{2^{k}-1}{k!} R\,. \end{equation*}
\begin{equation*} \textrm{Var}(\xi(\mathbb Y))-\lambda(\mathbb Y) \leq \sum_{i=1}^{k-1} \frac{1}{k!} \binom{k}{i} R \leq \frac{2^{k}-1}{k!} R\,. \end{equation*}
These inequalities combined with (3.10) and (3.11) deliver the assertion.
Acknowledgements
The authors would like to thank Chinmoy Bhattacharjee, Ilya Molchanov, and Matthias Schulte for valuable comments. The authors are also thankful to one anonymous referee for precise comments.
Funding information
This research was supported by the Swiss National Science Foundation, grant number 200021_175584.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.