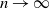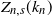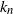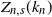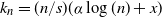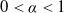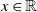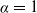1. Introduction
The coupon collector’s problem is an old problem of probability theory which in its simplest form dates back to de Moivre, Laplace, and Euler [Reference De Moivre4, Reference Euler6, Reference Laplace10]. While de Moivre used a die with s faces to pose the problem, Euler and Laplace used a lottery interpretation as motivation. However, a more recent example for a situation in which the coupon collector’s problem occurs is the collection of pictures of the participating players of all teams before and during every World Cup. Typically, fans can buy the pictures in packages of five or six. Two natural questions which arise are: How many packages need to be bought to get the full or a specific portion of the full set of players? How many stickers are missing after buying k packages? The first question was studied, for example, in [Reference Baum and Billingsley3, Reference Johnson and Kotz8, Reference Kolchin, Sevastianov and Chistiakov9, Reference Stadje18]. In the work at hand we will deal with the latter of the two problems. The version of the coupon collector’s problem we consider can be described as follows. Assume there are n different coupons. At each time we draw s of these n coupons, where we assume that each of the
![]() $\left(\tiny\begin{array}{c}n\\s\end{array}\right)$
choices occurs with the same probability. We are then interested in the distribution of the number
$\left(\tiny\begin{array}{c}n\\s\end{array}\right)$
choices occurs with the same probability. We are then interested in the distribution of the number
![]() $Z_{n,s}(k_n)$
of coupons that have not been drawn in the first
$Z_{n,s}(k_n)$
of coupons that have not been drawn in the first
![]() $k=k_n$
drawings. In a conceptually equivalent interpretation the n coupons are represented by n different cells numbered
$k=k_n$
drawings. In a conceptually equivalent interpretation the n coupons are represented by n different cells numbered
![]() $1, \ldots, n$
, and in each drawing we place s particles into s distinct cells; see Fig. 1. We are then interested in the distribution of the number
$1, \ldots, n$
, and in each drawing we place s particles into s distinct cells; see Fig. 1. We are then interested in the distribution of the number
![]() $Z_{n,s}(k_n)$
of empty cells after
$Z_{n,s}(k_n)$
of empty cells after
![]() $k=k_n$
drawings.
$k=k_n$
drawings.

Figure 1. Illustration of the cell interpretation with
![]() $n=7$
and
$n=7$
and
![]() $s=4$
in the first three drawings.
$s=4$
in the first three drawings.
The behaviour of
![]() $Z_{n,s}(k_n)$
for the different regimes of
$Z_{n,s}(k_n)$
for the different regimes of
![]() $k_n$
has been the subject of numerous research works over the years. In [Reference Mahmoud11] convergence towards a normal limit is proved for the sublinear and linear regime, i.e. for
$k_n$
has been the subject of numerous research works over the years. In [Reference Mahmoud11] convergence towards a normal limit is proved for the sublinear and linear regime, i.e. for
![]() $k_n= o(n)$
and
$k_n= o(n)$
and
![]() $k_n=\alpha n$
, respectively. In [Reference Smythe17] the author proves a central limit theorem for a generalised coupon collector’s problem allowing for random package sizes S in the lower superlinear regime, i.e. for
$k_n=\alpha n$
, respectively. In [Reference Smythe17] the author proves a central limit theorem for a generalised coupon collector’s problem allowing for random package sizes S in the lower superlinear regime, i.e. for
![]() ${k_n}/{n}\rightarrow \infty$
and
${k_n}/{n}\rightarrow \infty$
and
![]() $\limsup_n {k_n}/({n \log(n)}) < {1}/{\mathbb{E}[S]}$
using a martingale representation. In [Reference Mikhailov13] the method of moments is used to prove normal approximation for the case where
$\limsup_n {k_n}/({n \log(n)}) < {1}/{\mathbb{E}[S]}$
using a martingale representation. In [Reference Mikhailov13] the method of moments is used to prove normal approximation for the case where
![]() $n[({k_n s})/{n}]^r \rightarrow \infty$
for all
$n[({k_n s})/{n}]^r \rightarrow \infty$
for all
![]() $r \in \mathbb{N}$
and
$r \in \mathbb{N}$
and
![]() $\mathbb{E}[Z_{n,s}(k_n)] \rightarrow \infty$
, which covers our regime of normal approximation introduced below. However, no rates of convergence are given in either of the works mentioned so far. In [Reference Vatutin and Mikhailov19] the authors deduce rates of convergence in the Kolmogorov distance towards a normal limit for
$\mathbb{E}[Z_{n,s}(k_n)] \rightarrow \infty$
, which covers our regime of normal approximation introduced below. However, no rates of convergence are given in either of the works mentioned so far. In [Reference Vatutin and Mikhailov19] the authors deduce rates of convergence in the Kolmogorov distance towards a normal limit for
![]() $k_n=o(n \log(n))$
which are of order
$k_n=o(n \log(n))$
which are of order
![]() $1/\sqrt{\textrm{var}(Z_{n,s}(k_n))}$
and thus optimal by a general result of Englund [Reference Englund5, p. 692], which shows that for integer-valued random variables such as
$1/\sqrt{\textrm{var}(Z_{n,s}(k_n))}$
and thus optimal by a general result of Englund [Reference Englund5, p. 692], which shows that for integer-valued random variables such as
![]() $Z_{n,s}(k_n)$
the order of this rate cannot be improved. We complement these bounds in the case where
$Z_{n,s}(k_n)$
the order of this rate cannot be improved. We complement these bounds in the case where
![]() $k_n$
is assumed to be of the form
$k_n$
is assumed to be of the form
![]() $k_n=({n}/{s})(\alpha \log(n)+x)$
for some
$k_n=({n}/{s})(\alpha \log(n)+x)$
for some
![]() $\alpha \in (0,1)$
and
$\alpha \in (0,1)$
and
![]() $x \in \mathbb{R}$
. In the case
$x \in \mathbb{R}$
. In the case
![]() $\alpha=1$
, i.e. if
$\alpha=1$
, i.e. if
![]() $k_n = ({n}/{s})({\log}(n)+x)$
, the author in [Reference Mikhailov12] uses the Stein–Chen method to prove convergence towards a Poisson limit for the number of cells containing exactly r particles in a more general setting allowing for multiple particles being placed in one cell at each step. The same question is also studied in [Reference Schilling and Henze16], and a Poisson limit is deduced. The same work shows that for the special case
$k_n = ({n}/{s})({\log}(n)+x)$
, the author in [Reference Mikhailov12] uses the Stein–Chen method to prove convergence towards a Poisson limit for the number of cells containing exactly r particles in a more general setting allowing for multiple particles being placed in one cell at each step. The same question is also studied in [Reference Schilling and Henze16], and a Poisson limit is deduced. The same work shows that for the special case
![]() $r=0$
the condition of equally probable group drawings can be relaxed to a certain extent without losing the limiting Poisson distribution. In [Reference Barbour, Holst and Janson2, Theorem 6.F] the authors also prove rates of convergence of order
$r=0$
the condition of equally probable group drawings can be relaxed to a certain extent without losing the limiting Poisson distribution. In [Reference Barbour, Holst and Janson2, Theorem 6.F] the authors also prove rates of convergence of order
![]() ${\log(n)}/{n}$
towards a Poisson distribution in this regime, which are optimal in view of [Reference Barbour, Holst and Janson2, Theorem 3.D]. For
${\log(n)}/{n}$
towards a Poisson distribution in this regime, which are optimal in view of [Reference Barbour, Holst and Janson2, Theorem 3.D]. For
![]() $r=0$
this covers our setting of Poisson approximation with the same rates, which are included here only for completeness and to demonstrate that both limit theorems can be based on the same coupling argument.
$r=0$
this covers our setting of Poisson approximation with the same rates, which are included here only for completeness and to demonstrate that both limit theorems can be based on the same coupling argument.
As explained above, there exists a sharp asymptotic distributional phase transition at
![]() $\alpha=1$
in the sense that for
$\alpha=1$
in the sense that for
![]() $\alpha \in (0,1)$
the random variable
$\alpha \in (0,1)$
the random variable
![]() $Z_{n,s}(k_n)$
asymptotically follows a normal distribution, whereas for
$Z_{n,s}(k_n)$
asymptotically follows a normal distribution, whereas for
![]() $\alpha=1$
we obtain a Poisson limit. However, in both cases we use Stein’s method in combination with the same size-biased coupling construction to prove upper bounds on the distance between
$\alpha=1$
we obtain a Poisson limit. However, in both cases we use Stein’s method in combination with the same size-biased coupling construction to prove upper bounds on the distance between
![]() $Z_{n,s}(k_n)$
and a Gaussian or Poisson random variable, respectively. Our results are presented in the next section, while the coupling construction is explained in Section 3. The proof of the normal approximation result for
$Z_{n,s}(k_n)$
and a Gaussian or Poisson random variable, respectively. Our results are presented in the next section, while the coupling construction is explained in Section 3. The proof of the normal approximation result for
![]() $\alpha\in(0,1)$
is the content of Section 4, while the Poisson limit theorem is derived in Section 5.
$\alpha\in(0,1)$
is the content of Section 4, while the Poisson limit theorem is derived in Section 5.
2. Results
Denote by
![]() $(C_i)_{i=1,\ldots n}$
the collection of cells in the coupon collector’s problem, and let
$(C_i)_{i=1,\ldots n}$
the collection of cells in the coupon collector’s problem, and let
![]() $Z_{n,s}(k_n)$
be the number of empty cells after
$Z_{n,s}(k_n)$
be the number of empty cells after
![]() $k_n$
drawings, i.e.
$k_n$
drawings, i.e.
![]() $Z_{n,s}(k_n) = \sum_{j=1}^{n} \mathbf{1}_{E_{n,j}(k_n)}$
, where
$Z_{n,s}(k_n) = \sum_{j=1}^{n} \mathbf{1}_{E_{n,j}(k_n)}$
, where
![]() $E_{n,j}(k) = \{|C_j|=0$
after
$E_{n,j}(k) = \{|C_j|=0$
after
![]() $k_n$
drawings
$k_n$
drawings
![]() $\}$
and where
$\}$
and where
![]() $|C_j|$
stands for the number of particles in cell
$|C_j|$
stands for the number of particles in cell
![]() $C_j$
. Moreover, for two random variables X and Y we denote by
$C_j$
. Moreover, for two random variables X and Y we denote by
the Wasserstein distance between X and Y, where the supremum runs over all Lipschitz functions
![]() $h\,:\,\mathbb{R}\to\mathbb{R}$
with Lipschitz constant less than or equal to one. We consider the case where
$h\,:\,\mathbb{R}\to\mathbb{R}$
with Lipschitz constant less than or equal to one. We consider the case where
![]() $k_n = ({n}/{s})(\alpha\log(n)+x)$
for fixed
$k_n = ({n}/{s})(\alpha\log(n)+x)$
for fixed
![]() $s \in \mathbb{N}$
,
$s \in \mathbb{N}$
,
![]() $x \in \mathbb{R}$
, and
$x \in \mathbb{R}$
, and
![]() $\alpha \in (0,1)$
. Note that since
$\alpha \in (0,1)$
. Note that since
![]() $k_n$
denotes the number of drawings, we always assume implicitly that
$k_n$
denotes the number of drawings, we always assume implicitly that
![]() $k_n$
is an integer; in particular we assume that n is large enough that
$k_n$
is an integer; in particular we assume that n is large enough that
![]() $k_n \geq 0$
. Furthermore, we define the centred and normalised random variables
$k_n \geq 0$
. Furthermore, we define the centred and normalised random variables
Throughout the paper we use the notation
![]() $C(x_1, x_2,\ldots\!)$
to indicate that a constant
$C(x_1, x_2,\ldots\!)$
to indicate that a constant
![]() $C\in(0,\infty)$
only depends on parameters
$C\in(0,\infty)$
only depends on parameters
![]() $x_1, x_2, \ldots$
of the model.
$x_1, x_2, \ldots$
of the model.
Theorem 1.
Put
![]() $k_n= ({n}/{s})(\alpha\log(n)+x)$
for some
$k_n= ({n}/{s})(\alpha\log(n)+x)$
for some
![]() $s\in\mathbb{N}$
,
$s\in\mathbb{N}$
,
![]() $x \in \mathbb{R}$
, and
$x \in \mathbb{R}$
, and
![]() $\alpha \in (0,1)$
. Let
$\alpha \in (0,1)$
. Let
![]() $Z_{n,s}(k_n)$
be the number of empty cells after
$Z_{n,s}(k_n)$
be the number of empty cells after
![]() $k_n$
drawings as introduced above, and denote by G a standard Gaussian random variable. Then there exist constants
$k_n$
drawings as introduced above, and denote by G a standard Gaussian random variable. Then there exist constants
![]() $C = C(x,\alpha) \in (0, \infty)$
and
$C = C(x,\alpha) \in (0, \infty)$
and
![]() $N = N(s,x,\alpha) \in \mathbb{N}$
such that, for all
$N = N(s,x,\alpha) \in \mathbb{N}$
such that, for all
![]() $n \geq N$
,
$n \geq N$
,
After this general bound we now consider the situation in which s behaves like a constant multiple of a non-negative power of n. In particular, this covers the case where s is constant. We denote by [y] the integer part of a real number
![]() $y\in\mathbb{R}$
.
$y\in\mathbb{R}$
.
Corollary 1.
In the situation of Theorem 1, suppose additionally that s is of the form
![]() $s = [s_0n^\beta]$
for some
$s = [s_0n^\beta]$
for some
![]() $\beta \in \big[0,\frac{1-\alpha}{4}\big)$
and
$\beta \in \big[0,\frac{1-\alpha}{4}\big)$
and
![]() $s_0 \geq 1$
. Then,
$s_0 \geq 1$
. Then,
 \begin{equation*} d_{\textrm{W}}(\tilde{Z}_{n,s},G) \leq \begin{cases} C{\sqrt{\log n}/n^{\alpha}} & \quad for\ \alpha\in\big(0,\frac{1}{3}\big], \\[5pt] C{n^{-{(1-\alpha)/2}+2\beta}} & \quad for\ \alpha\in\big(\frac{1}{3},1\big) \end{cases} \end{equation*}
\begin{equation*} d_{\textrm{W}}(\tilde{Z}_{n,s},G) \leq \begin{cases} C{\sqrt{\log n}/n^{\alpha}} & \quad for\ \alpha\in\big(0,\frac{1}{3}\big], \\[5pt] C{n^{-{(1-\alpha)/2}+2\beta}} & \quad for\ \alpha\in\big(\frac{1}{3},1\big) \end{cases} \end{equation*}
for
![]() $n\geq N$
, where
$n\geq N$
, where
![]() $C = C(x,\alpha,s_0)\in(0,\infty)$
,
$C = C(x,\alpha,s_0)\in(0,\infty)$
,
![]() $N = N(x,\alpha,s_0,\beta)\in(0,\infty)$
. In particular, if
$N = N(x,\alpha,s_0,\beta)\in(0,\infty)$
. In particular, if
![]() $s \equiv s_0 \geq 1$
is constant,
$s \equiv s_0 \geq 1$
is constant,
 \begin{equation*} d_{\textrm{W}}(\tilde{Z}_{n,s},G) \leq \begin{cases} C{\sqrt{\log n}/n^{\alpha}} & \quad for\ \alpha\in\big(0,\frac{1}{3}\big], \\[5pt] C{n^{-{(1-\alpha)/2}}} & \quad for\ \alpha\in\big(\frac{1}{3},1\big). \end{cases} \end{equation*}
\begin{equation*} d_{\textrm{W}}(\tilde{Z}_{n,s},G) \leq \begin{cases} C{\sqrt{\log n}/n^{\alpha}} & \quad for\ \alpha\in\big(0,\frac{1}{3}\big], \\[5pt] C{n^{-{(1-\alpha)/2}}} & \quad for\ \alpha\in\big(\frac{1}{3},1\big). \end{cases} \end{equation*}
Proof. The bounds are immediate from Theorem 1 by plugging in the particular choice for s.
Remark 1.
-
(i) Since
 $n^{-({1-\alpha})/{2}}$
is of the same order as
$n^{-({1-\alpha})/{2}}$
is of the same order as
 $1/\sqrt{\textrm{var}(Z_{n,s}(k_n))}$
, we believe that the rate in Corollary 1 is optimal in the regime
$1/\sqrt{\textrm{var}(Z_{n,s}(k_n))}$
, we believe that the rate in Corollary 1 is optimal in the regime
 $\alpha\in\big(\frac13,1\big)$
and if s is constant (
$\alpha\in\big(\frac13,1\big)$
and if s is constant (
 $\beta=0$
). We leave it as an open problem to decide whether or not the rate is optimal for
$\beta=0$
). We leave it as an open problem to decide whether or not the rate is optimal for
 $\alpha\in\big(0,\frac13\big]$
. On the other hand, Remark 4 shows that in this situation the rate cannot be improved by arguments based on the general normal approximation bound (7) (although this does, of course, exclude the possibility of improving the bound by other methods).
$\alpha\in\big(0,\frac13\big]$
. On the other hand, Remark 4 shows that in this situation the rate cannot be improved by arguments based on the general normal approximation bound (7) (although this does, of course, exclude the possibility of improving the bound by other methods). -
(ii) We might ask whether the Wasserstein distance in Theorem 1 and Corollary 1 can be replaced by the Kolmogorov distance
As explained in Remark 3 in more detail, this is not possible by means of the size-biased coupling approach of Stein’s method for normal approximation using our coupling construction. In fact, the resulting bound in this case does not even tend to zero with n. On the other hand, a presumably suboptimal bound follows directly from the fact that the Kolmogorov distance can always be bounded by the square root of the Wasserstein distance. \begin{equation*}d_{K}\big(\tilde{Z}_{n,s}(k_n), N\big) = \sup_{u\in\mathbb{R}}\big|\mathbb{P}\big(\tilde{Z}_{n,s}(k_n)\leq u\big) - \mathbb{P}(N\leq u)\big|.\end{equation*}
\begin{equation*}d_{K}\big(\tilde{Z}_{n,s}(k_n), N\big) = \sup_{u\in\mathbb{R}}\big|\mathbb{P}\big(\tilde{Z}_{n,s}(k_n)\leq u\big) - \mathbb{P}(N\leq u)\big|.\end{equation*}
-
(iii) Remark 5 demonstrates that it is possible to make the constants C and N appearing in Theorem 1 (and thus Corollary 1) fully explicit in terms of the parameters x and
 $\alpha$
. However, since the resulting expressions are rather involved, we decided to present our results in a simplified form. A similar comment also applies to the constants appearing in Theorem 2.
$\alpha$
. However, since the resulting expressions are rather involved, we decided to present our results in a simplified form. A similar comment also applies to the constants appearing in Theorem 2.
The next result complements Theorem 1 by considering the case
![]() $\alpha=1$
for which the upper bound (2) does not tend to zero as
$\alpha=1$
for which the upper bound (2) does not tend to zero as
![]() $n\to\infty$
. As emphasised already, the result is known from [Reference Barbour, Holst and Janson2] and is included here only for completeness. As above, for two random variables X and Y we denote by
$n\to\infty$
. As emphasised already, the result is known from [Reference Barbour, Holst and Janson2] and is included here only for completeness. As above, for two random variables X and Y we denote by
the total variation distance between X and Y, where the supremum is taken over all Borel sets
![]() $A\subset\mathbb{R}$
.
$A\subset\mathbb{R}$
.
Theorem 2.
Put
![]() $k_n= ({n}/{s})({\log}(n)+x)$
for some
$k_n= ({n}/{s})({\log}(n)+x)$
for some
![]() $s\in\mathbb{N}$
and
$s\in\mathbb{N}$
and
![]() $x \in \mathbb{R}$
. Let
$x \in \mathbb{R}$
. Let
![]() $Z_{n,s}(k_n)$
be the number of empty cells after
$Z_{n,s}(k_n)$
be the number of empty cells after
![]() $k_n$
drawings, and denote by W a Poisson random variable with parameter
$k_n$
drawings, and denote by W a Poisson random variable with parameter
![]() $\lambda_n = \mathbb{E}[Z_{n,s}(k_n)]$
. Then there exist constants
$\lambda_n = \mathbb{E}[Z_{n,s}(k_n)]$
. Then there exist constants
![]() $\tilde{C} = \tilde{C}(s,x) \in (0, \infty)$
and
$\tilde{C} = \tilde{C}(s,x) \in (0, \infty)$
and
![]() $\tilde{N} = \tilde{N}(s,x) \in \mathbb{N}$
such that, for all
$\tilde{N} = \tilde{N}(s,x) \in \mathbb{N}$
such that, for all
![]() $n \geq \tilde{N}$
,
$n \geq \tilde{N}$
,
Remark 2. It has been shown in [Reference Barbour, Holst and Janson2] that the rate in Theorem 2 is optimal in the sense that we can find other constants
![]() $\widehat{C},\widehat{N}\in(0,\infty)$
, depending on s and x only, such that
$\widehat{C},\widehat{N}\in(0,\infty)$
, depending on s and x only, such that
![]() $d_\textrm{TV}(Z_{n,s}(k_n), W) \geq \widehat{C}\,{\log(n)}/{n}$
for all
$d_\textrm{TV}(Z_{n,s}(k_n), W) \geq \widehat{C}\,{\log(n)}/{n}$
for all
![]() $n\geq\widehat{N}$
.
$n\geq\widehat{N}$
.
For the proof of both results we use Stein’s method in combination with a size-biased coupling. We start by describing this coupling in the next section, which can be regarded as a particular instant of the construction in [Reference Neal14, p. 623] (choosing
![]() $p_{ni}=1/n$
there).
$p_{ni}=1/n$
there).
3. Coupling construction
We are dealing with the coupon collector’s problem with n coupons, which can be interpreted as n distinct cells. At each time step we place a fixed number
![]() $s \leq n$
of particles in s different cells. In order to keep track of when particles are placed into cells, we label all particles in the mth drawing with the letter m. Now, after
$s \leq n$
of particles in s different cells. In order to keep track of when particles are placed into cells, we label all particles in the mth drawing with the letter m. Now, after
![]() $k_n$
placements, we choose one of the n cells, which we denote by
$k_n$
placements, we choose one of the n cells, which we denote by
![]() $C_I$
, uniformly at random and take all particles out of it. For a particle labelled j taken from
$C_I$
, uniformly at random and take all particles out of it. For a particle labelled j taken from
![]() $C_I$
we now choose one of the
$C_I$
we now choose one of the
![]() $n-s$
cells not containing a particle with label j uniformly and place the particle into it. We proceed in the same manner until all particles from cell I have been redistributed into the remaining
$n-s$
cells not containing a particle with label j uniformly and place the particle into it. We proceed in the same manner until all particles from cell I have been redistributed into the remaining
![]() $n-1$
cells; see Fig. 2.
$n-1$
cells; see Fig. 2.

Figure 2. Illustration of the coupling construction (continuation of Fig. 1); the artificially isolated cell with label I is the dashed one.
Denote by
![]() $F_{n,j}^I$
the event that at least one particle from cell I is placed into cell j, and put
$F_{n,j}^I$
the event that at least one particle from cell I is placed into cell j, and put
![]() $\bar{F}_{n,j}^I\,:\!=\,\big(F_{n,j}^I\big)^{\textrm{c}}$
. Furthermore, we define
$\bar{F}_{n,j}^I\,:\!=\,\big(F_{n,j}^I\big)^{\textrm{c}}$
. Furthermore, we define
![]() $E^I_{n,j}(k_n)\,:\!=\, E_{n,j}(k_n) \cap \bar{F}_{n,j}^I$
. For any
$E^I_{n,j}(k_n)\,:\!=\, E_{n,j}(k_n) \cap \bar{F}_{n,j}^I$
. For any
![]() $j \neq I$
we then have
$j \neq I$
we then have
 \begin{align} \mathbb{P}\Big(E^I_{n,j}(k_n)\Big) & = \sum_{\ell=0}^{k_n} \mathbb{P}\Big(E_{n,j}(k_n)\cap \bar{F}_{n,j}^I\cap\{|C_I|=\ell\}\Big) \notag \\ & = \sum_{\ell=0}^{k_n} \mathbb{P}\Big( \bar{F}_{n,j}^I \mid E_{n,j}(k_n)\cap\{ |C_I|=\ell\}\Big) \mathbb{P}( |C_I|=\ell \mid E_{n,j}(k_n)) \mathbb{P}\big(E_{n,j}(k_n)\big).\end{align}
\begin{align} \mathbb{P}\Big(E^I_{n,j}(k_n)\Big) & = \sum_{\ell=0}^{k_n} \mathbb{P}\Big(E_{n,j}(k_n)\cap \bar{F}_{n,j}^I\cap\{|C_I|=\ell\}\Big) \notag \\ & = \sum_{\ell=0}^{k_n} \mathbb{P}\Big( \bar{F}_{n,j}^I \mid E_{n,j}(k_n)\cap\{ |C_I|=\ell\}\Big) \mathbb{P}( |C_I|=\ell \mid E_{n,j}(k_n)) \mathbb{P}\big(E_{n,j}(k_n)\big).\end{align}
Note that by construction we have
since conditioning on the event
![]() $E_{n,j}(k_n)$
simply means that we can only place particles in
$E_{n,j}(k_n)$
simply means that we can only place particles in
![]() $n-1$
instead of n cells. In addition,
$n-1$
instead of n cells. In addition,
since for each of the particles from cell I the probability that it is placed into an originally empty cell is
![]() ${1}/({n-s})$
. Putting these expressions back into (3), we obtain
${1}/({n-s})$
. Putting these expressions back into (3), we obtain
 \begin{align} \mathbb{P}\big(E_{n,j}^{I}(k_n)\big) & = \sum_{\ell=0}^{k_n}\left(\begin{array}{c}k_n\\\ell\end{array}\right)\bigg(\frac{s}{n-1}\bigg)^\ell \bigg(1-\frac{s}{n-1}\bigg)^{k_n-\ell}\bigg(1-\frac{1}{n-s}\bigg)^\ell \bigg(1-\frac{s}{n}\bigg)^{k_n} \notag \\ & = \bigg(1-\frac{s}{n-1}\bigg)^{k_n} = \mathbb{P}\big(E_{n,j}(k_n) \mid E_{n,i}(k_n)\big)\end{align}
\begin{align} \mathbb{P}\big(E_{n,j}^{I}(k_n)\big) & = \sum_{\ell=0}^{k_n}\left(\begin{array}{c}k_n\\\ell\end{array}\right)\bigg(\frac{s}{n-1}\bigg)^\ell \bigg(1-\frac{s}{n-1}\bigg)^{k_n-\ell}\bigg(1-\frac{1}{n-s}\bigg)^\ell \bigg(1-\frac{s}{n}\bigg)^{k_n} \notag \\ & = \bigg(1-\frac{s}{n-1}\bigg)^{k_n} = \mathbb{P}\big(E_{n,j}(k_n) \mid E_{n,i}(k_n)\big)\end{align}
for any
![]() $i \neq j$
. We thus conclude that the random variable
$i \neq j$
. We thus conclude that the random variable
 \begin{equation*} Z^I_{n,s}(k_n) \,:\!=\, 1 + \sum_{\substack{j=1\\ j \neq I}}^{n} \mathbf{1}_{E^I_{n,j}(k_n)}\end{equation*}
\begin{equation*} Z^I_{n,s}(k_n) \,:\!=\, 1 + \sum_{\substack{j=1\\ j \neq I}}^{n} \mathbf{1}_{E^I_{n,j}(k_n)}\end{equation*}
has the
![]() $Z_{n,s}(k_n)$
-size-biased distribution, meaning that
$Z_{n,s}(k_n)$
-size-biased distribution, meaning that
see [Reference Arratia, Goldstein and Kochman1].
Remark 3. Theorem 5.6 in [Reference Arratia, Goldstein and Kochman1] provides a bound on the Kolmogorov distance between
![]() $\tilde{Z}_{n,s}(k_n)$
and a standard Gaussian random variable using a size-biased coupling. However, for this to yield a central limit theorem we need
$\tilde{Z}_{n,s}(k_n)$
and a standard Gaussian random variable using a size-biased coupling. However, for this to yield a central limit theorem we need
![]() $|Z^I_{n,s}-Z_{n,s}| = o(\sqrt{n})$
almost surely as
$|Z^I_{n,s}-Z_{n,s}| = o(\sqrt{n})$
almost surely as
![]() $n\to\infty$
. For the coupling described above we have
$n\to\infty$
. For the coupling described above we have
![]() $|Z^I_{n,s}-Z_{n,s}| = n-s-1$
if in all
$|Z^I_{n,s}-Z_{n,s}| = n-s-1$
if in all
![]() $k_n$
drawings the same s cells are filled and the remaining
$k_n$
drawings the same s cells are filled and the remaining
![]() $n-s$
cells are filled when redistributing the
$n-s$
cells are filled when redistributing the
![]() $k_n$
particles of one of the filled cells. Consequently, the result in [Reference Arratia, Goldstein and Kochman1] does not lead to a meaningful bound on the Komogorov distance, as explained in Remark 1(ii).
$k_n$
particles of one of the filled cells. Consequently, the result in [Reference Arratia, Goldstein and Kochman1] does not lead to a meaningful bound on the Komogorov distance, as explained in Remark 1(ii).
4. Proof of Theorem 1
Following [Reference Goldstein and Rinott7, Theorem 1.1], the Wasserstein distance between
![]() $\tilde{Z}_{n,s}=\tilde{Z}_{n,s}(k_n)$
as defined in (1) and a standard Gaussian random variable G is bounded by
$\tilde{Z}_{n,s}=\tilde{Z}_{n,s}(k_n)$
as defined in (1) and a standard Gaussian random variable G is bounded by
where
![]() $\mathcal{C}_n(k_n)$
denotes the configuration of the n cells after
$\mathcal{C}_n(k_n)$
denotes the configuration of the n cells after
![]() $k_n$
drawings,
$k_n$
drawings,
![]() $\lambda_n=\mathbb{E}[Z_{n,s}(k_n)]$
, and
$\lambda_n=\mathbb{E}[Z_{n,s}(k_n)]$
, and
![]() $\sigma_n^2= \textrm{var}(Z_{n,s}(k_n))$
. In the next sections we further bound the right-hand side of (7) by dealing with the individual terms.
$\sigma_n^2= \textrm{var}(Z_{n,s}(k_n))$
. In the next sections we further bound the right-hand side of (7) by dealing with the individual terms.
4.1. Expectation and variance
We start by bounding from above the expectation, and from below the variance, of
![]() $Z_{n,s}$
. First, we note that, for
$Z_{n,s}$
. First, we note that, for
![]() $k_n=\frac{n}{s}(\alpha\log(n)+x)$
,
$k_n=\frac{n}{s}(\alpha\log(n)+x)$
,
where we write
![]() $f(n) \sim g(n)$
for two functions
$f(n) \sim g(n)$
for two functions
![]() $f,g\,:\,\mathbb{N}\to\mathbb{R}$
if
$f,g\,:\,\mathbb{N}\to\mathbb{R}$
if
![]() $\lim_{n\rightarrow \infty} [{f(n)}/{g(n)}] = 1$
. Thus,
$\lim_{n\rightarrow \infty} [{f(n)}/{g(n)}] = 1$
. Thus,
 \begin{equation} \mathbb{E}[Z_{n,s}(k_n)] = \sum_{j=1}^{n}\mathbb{P}(E_{n,j}(k_n)) \sim \textrm{e}^{-x}n^{1-\alpha}.\end{equation}
\begin{equation} \mathbb{E}[Z_{n,s}(k_n)] = \sum_{j=1}^{n}\mathbb{P}(E_{n,j}(k_n)) \sim \textrm{e}^{-x}n^{1-\alpha}.\end{equation}
In particular,
![]() $\mathbb{P}(E_{n,j}(k_n)) \leq {e^{-x}}{n^{-\alpha}}$
for all
$\mathbb{P}(E_{n,j}(k_n)) \leq {e^{-x}}{n^{-\alpha}}$
for all
![]() $n \geq 1$
. Similarly, we obtain
$n \geq 1$
. Similarly, we obtain
 \begin{align} \bigg(1-\frac{s}{n}\bigg)^{k_n} - \bigg(1-\frac{s}{n-1}\bigg)^{k_n} & = \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(1-\bigg(\frac{(n-1-s)n}{(n-1)(n-s)}\bigg)^{k_n}\bigg) \notag \\ & \leq \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(-k_n\bigg(\frac{(n-1-s)n}{(n-1)(n-s)}-1\bigg)\bigg) \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \, k_n\, \frac{(n-1)(n-s)-(n-1-s)n}{(n-1)(n-s)} \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \frac{k_ns}{(n-1)(n-s)} \notag \\ & \leq \frac{2 \textrm{e}^{-x} (\alpha \log(n)+x)}{n^{1+\alpha}} \end{align}
\begin{align} \bigg(1-\frac{s}{n}\bigg)^{k_n} - \bigg(1-\frac{s}{n-1}\bigg)^{k_n} & = \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(1-\bigg(\frac{(n-1-s)n}{(n-1)(n-s)}\bigg)^{k_n}\bigg) \notag \\ & \leq \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(-k_n\bigg(\frac{(n-1-s)n}{(n-1)(n-s)}-1\bigg)\bigg) \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \, k_n\, \frac{(n-1)(n-s)-(n-1-s)n}{(n-1)(n-s)} \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \frac{k_ns}{(n-1)(n-s)} \notag \\ & \leq \frac{2 \textrm{e}^{-x} (\alpha \log(n)+x)}{n^{1+\alpha}} \end{align}
for all
![]() $n \geq n_1$
for some
$n \geq n_1$
for some
![]() $n_1= n_1(\alpha,s) \in \mathbb{N}$
, where we have used that
$n_1= n_1(\alpha,s) \in \mathbb{N}$
, where we have used that
for
![]() $z \in (0,1)$
. Using that
$z \in (0,1)$
. Using that
![]() $\textrm{var}({\bf 1}_A)=\mathbb{P}(A)(1-\mathbb{P}(A))$
and
$\textrm{var}({\bf 1}_A)=\mathbb{P}(A)(1-\mathbb{P}(A))$
and
![]() $\operatorname{Cov}({\bf 1}_A,{\bf 1}_B)=\mathbb{P}(A\cap B)-\mathbb{P}(A)\mathbb{P}(B)=\mathbb{P}(B)(\mathbb{P}(A\mid B)-\mathbb{P}(A))$
, we see that
$\operatorname{Cov}({\bf 1}_A,{\bf 1}_B)=\mathbb{P}(A\cap B)-\mathbb{P}(A)\mathbb{P}(B)=\mathbb{P}(B)(\mathbb{P}(A\mid B)-\mathbb{P}(A))$
, we see that
 \begin{align*} \textrm{var}(Z_{n,s}) & = \sum_{j=1}^{n} \textrm{var}\big[\mathbf{1}_{E_{n,j}(k_n)}\big] + \sum_{j=1}^{n} \sum_{\substack{i=1 \\ i\neq j}}^n \operatorname{Cov}\big[\mathbf{1}_{E_{n,j}(k_n)}, \mathbf{1}_{E_{n,i}(k_n)}\big] \\ & = \sum_{j=1}^n\mathbb{P}(E_{n,j}(k_n))(1-\mathbb{P}(E_{n,j}(k_n))) \\ & \quad + \sum_{j=1}^{n} \sum_{\substack{i=1 \\ i\neq j}}^n [\mathbb{P}(E_{n,i}(k_n))(\mathbb{P}(E_{n,j}(k_n) \mid E_{n,i}(k_n))-\mathbb{P}(E_{n,j}(k_n)))] \\ & = \bigg[1-\bigg(1-\frac{s}{n}\bigg)^{k_n} + (n-1)\bigg( \bigg(1-\frac{s}{n-1}\bigg)^{k_n} -\bigg(1-\frac{s}{n}\bigg)^{k_n} \bigg)\bigg]\mathbb{E}[Z_{n,s}].\end{align*}
\begin{align*} \textrm{var}(Z_{n,s}) & = \sum_{j=1}^{n} \textrm{var}\big[\mathbf{1}_{E_{n,j}(k_n)}\big] + \sum_{j=1}^{n} \sum_{\substack{i=1 \\ i\neq j}}^n \operatorname{Cov}\big[\mathbf{1}_{E_{n,j}(k_n)}, \mathbf{1}_{E_{n,i}(k_n)}\big] \\ & = \sum_{j=1}^n\mathbb{P}(E_{n,j}(k_n))(1-\mathbb{P}(E_{n,j}(k_n))) \\ & \quad + \sum_{j=1}^{n} \sum_{\substack{i=1 \\ i\neq j}}^n [\mathbb{P}(E_{n,i}(k_n))(\mathbb{P}(E_{n,j}(k_n) \mid E_{n,i}(k_n))-\mathbb{P}(E_{n,j}(k_n)))] \\ & = \bigg[1-\bigg(1-\frac{s}{n}\bigg)^{k_n} + (n-1)\bigg( \bigg(1-\frac{s}{n-1}\bigg)^{k_n} -\bigg(1-\frac{s}{n}\bigg)^{k_n} \bigg)\bigg]\mathbb{E}[Z_{n,s}].\end{align*}
Applying (10), we conclude that there exists a constant
![]() ${c_1(x)} \in (0, \infty)$
such that, for
${c_1(x)} \in (0, \infty)$
such that, for
![]() $n \geq n_1$
, we have the lower variance bound
$n \geq n_1$
, we have the lower variance bound
4.2. Bounding
 $\textrm{var}\big(\mathbb{E}\big[Z_{n,s}-Z^I_{n,s}\vert_n(k_n) \big]\big)$
$\textrm{var}\big(\mathbb{E}\big[Z_{n,s}-Z^I_{n,s}\vert_n(k_n) \big]\big)$
For the variance of the conditional expectation on the right-hand side in (7) we obtain
 \begin{align} & \textrm{var}\big(\mathbb{E}\big[Z_{n,s}-Z^I_{n,s}\vert\mathcal{C}_n(k_n) \big]\big) = \textrm{var}\Bigg(\mathbb{E}\Bigg[\sum_{j=1}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I}\mid\mathcal{C}_n(k_n)\Bigg]\Bigg) \notag \\ & = \mathbb{E}\Bigg[\Bigg(\sum_{j=1}^n\mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big]\Bigg)^2\Bigg] - \mathbb{E}\Bigg[\sum_{j=1}^n \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big]\Bigg]^2 \notag \\ & = \mathbb{E}\Bigg[\sum_{j=1}^n \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big]^2\Bigg] \notag \\ & \ + \Bigg(\mathbb{E}\Bigg[\sum_{j=1}^n \sum_{\substack{i=1 \\ i\neq j}}^n \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big] \, \mathbb{E}\Big[\mathbf{1}_{E_{n,i}(k_n)\cap F_{n,i}^I} \mid \mathcal{C}_n(k_n) \Big]\Bigg] - \Bigg[\sum_{j=1}^n \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I}\Big]\Bigg]^2\Bigg) \notag \\ & =\!:\, T_1+T_2.\end{align}
\begin{align} & \textrm{var}\big(\mathbb{E}\big[Z_{n,s}-Z^I_{n,s}\vert\mathcal{C}_n(k_n) \big]\big) = \textrm{var}\Bigg(\mathbb{E}\Bigg[\sum_{j=1}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I}\mid\mathcal{C}_n(k_n)\Bigg]\Bigg) \notag \\ & = \mathbb{E}\Bigg[\Bigg(\sum_{j=1}^n\mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big]\Bigg)^2\Bigg] - \mathbb{E}\Bigg[\sum_{j=1}^n \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big]\Bigg]^2 \notag \\ & = \mathbb{E}\Bigg[\sum_{j=1}^n \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big]^2\Bigg] \notag \\ & \ + \Bigg(\mathbb{E}\Bigg[\sum_{j=1}^n \sum_{\substack{i=1 \\ i\neq j}}^n \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big] \, \mathbb{E}\Big[\mathbf{1}_{E_{n,i}(k_n)\cap F_{n,i}^I} \mid \mathcal{C}_n(k_n) \Big]\Bigg] - \Bigg[\sum_{j=1}^n \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I}\Big]\Bigg]^2\Bigg) \notag \\ & =\!:\, T_1+T_2.\end{align}
We start by dealing with
![]() $T_1$
. Note that, conditionally on the event
$T_1$
. Note that, conditionally on the event
![]() $E_{n,j}(k_n)$
,
$E_{n,j}(k_n)$
,
so that, with (11), we obtain
 \begin{equation*} T_1 = \mathbb{E}\Bigg[\sum_{j=1}^n \mathbf{1}_{E_{n,j}(k_n)} \bigg(1-\bigg(1-\frac{1}{n-s}\bigg)^{|C_I|}\bigg)^2\Bigg] \leq \frac{1}{(n-s)^2}\mathbb{E}\Bigg[\sum_{j=1}^n \mathbf{1}_{E_{n,j}(k_n)} \mid C_I|^2\Bigg].\end{equation*}
\begin{equation*} T_1 = \mathbb{E}\Bigg[\sum_{j=1}^n \mathbf{1}_{E_{n,j}(k_n)} \bigg(1-\bigg(1-\frac{1}{n-s}\bigg)^{|C_I|}\bigg)^2\Bigg] \leq \frac{1}{(n-s)^2}\mathbb{E}\Bigg[\sum_{j=1}^n \mathbf{1}_{E_{n,j}(k_n)} \mid C_I|^2\Bigg].\end{equation*}
Denoting by
![]() $D^I_m$
the event that a particle is placed into cell
$D^I_m$
the event that a particle is placed into cell
![]() $C_I$
in the mth drawing for some
$C_I$
in the mth drawing for some
![]() $m\in\{1,\ldots,k_n\}$
, we see that
$m\in\{1,\ldots,k_n\}$
, we see that
 \begin{align*} \mathbb{E}\big[\mathbf{1}_{E_{n,j}(k_n)} \mid C_I|^2\big] & = \mathbb{E}\Bigg[\mathbf{1}_{E_{n,j}(k_n)}\Bigg(\sum_{m=1}^{k_n}\mathbf{1}_{D_m^I} \Bigg)^2 \Bigg] \\ & = \mathbb{E}\Bigg[\sum_{m=1}^{k_n}\mathbf{1}_{E_{n,j}(k_n)}\mathbf{1}_{D_m^I} \Bigg] + \mathbb{E}\Bigg[\sum_{m=1}^{k_n} \sum_{\substack{r=1 \\ r\neq m}}^{k_n} \mathbf{1}_{E_{n,j}(k_n)}\mathbf{1}_{D_m^I}\mathbf{1}_{D_r^I}\Bigg] \\ & = \mathbb{P}(E_{n,j}(k_n)) \Bigg(\sum_{m=1}^{k_n}\mathbb{P}\Big(D_m^I \mid E_{n,j}(k_n)\Big) + \sum_{m=1}^{k_n} \sum_{\substack{r=1 \\ r\neq m}}^{k_n}\mathbb{P}\Big(D_m^I \cap D_r^I \mid E_{n,j}(k_n)\Big)\Bigg).\end{align*}
\begin{align*} \mathbb{E}\big[\mathbf{1}_{E_{n,j}(k_n)} \mid C_I|^2\big] & = \mathbb{E}\Bigg[\mathbf{1}_{E_{n,j}(k_n)}\Bigg(\sum_{m=1}^{k_n}\mathbf{1}_{D_m^I} \Bigg)^2 \Bigg] \\ & = \mathbb{E}\Bigg[\sum_{m=1}^{k_n}\mathbf{1}_{E_{n,j}(k_n)}\mathbf{1}_{D_m^I} \Bigg] + \mathbb{E}\Bigg[\sum_{m=1}^{k_n} \sum_{\substack{r=1 \\ r\neq m}}^{k_n} \mathbf{1}_{E_{n,j}(k_n)}\mathbf{1}_{D_m^I}\mathbf{1}_{D_r^I}\Bigg] \\ & = \mathbb{P}(E_{n,j}(k_n)) \Bigg(\sum_{m=1}^{k_n}\mathbb{P}\Big(D_m^I \mid E_{n,j}(k_n)\Big) + \sum_{m=1}^{k_n} \sum_{\substack{r=1 \\ r\neq m}}^{k_n}\mathbb{P}\Big(D_m^I \cap D_r^I \mid E_{n,j}(k_n)\Big)\Bigg).\end{align*}
Since all s-placements occur with the same probability, and conditioning on the event
![]() $E_{n,j}(k_n)$
simply means that we can only place particles into
$E_{n,j}(k_n)$
simply means that we can only place particles into
![]() $n-1$
cells, we have
$n-1$
cells, we have
![]() $\mathbb{P}\big(D_m^I \mid E_{n,j}(k_n)\big) = {s}/({n-1})$
. As the drawings are independent of each other,
$\mathbb{P}\big(D_m^I \mid E_{n,j}(k_n)\big) = {s}/({n-1})$
. As the drawings are independent of each other,
 \begin{align*} & \sum_{m=1}^{k_n}\mathbb{P}\big(D_m^I \mid E_{n,j}(k_n)\big) + \sum_{m=1}^{k_n} \sum_{\substack{r=1 \\ r\neq m}}^{k_n}\mathbb{P}\big(D_m^I \cap D_r^I \mid E_{n,j}(k_n)\big) \\ & = \sum_{m=1}^{k_n}\mathbb{P}\big(D_m^I \mid E_{n,j}(k_n)\big) + \sum_{m=1}^{k_n} \sum_{\substack{r=1 \\ r\neq m}}^{k_n}\mathbb{P}\big(D_m^I \mid E_{n,j}(k_n)\big) \mathbb{P}\big(D_r^I \mid E_{n,j}(k_n)\big) = \frac{k_n s}{n-1} + \frac{k_n (k_{n}-1)s^2}{(n-1)^2}.\end{align*}
\begin{align*} & \sum_{m=1}^{k_n}\mathbb{P}\big(D_m^I \mid E_{n,j}(k_n)\big) + \sum_{m=1}^{k_n} \sum_{\substack{r=1 \\ r\neq m}}^{k_n}\mathbb{P}\big(D_m^I \cap D_r^I \mid E_{n,j}(k_n)\big) \\ & = \sum_{m=1}^{k_n}\mathbb{P}\big(D_m^I \mid E_{n,j}(k_n)\big) + \sum_{m=1}^{k_n} \sum_{\substack{r=1 \\ r\neq m}}^{k_n}\mathbb{P}\big(D_m^I \mid E_{n,j}(k_n)\big) \mathbb{P}\big(D_r^I \mid E_{n,j}(k_n)\big) = \frac{k_n s}{n-1} + \frac{k_n (k_{n}-1)s^2}{(n-1)^2}.\end{align*}
Using (8), there exists a constant
![]() ${c_2(x)} \in (0,\infty)$
such that we can bound
${c_2(x)} \in (0,\infty)$
such that we can bound
![]() $T_1$
by
$T_1$
by
 \begin{align} T_1 & \leq \bigg(1-\frac{s}{n}\bigg)^{k_n}\frac{n}{(n-s)^2} \bigg(\frac{k_n s}{n-1} + \frac{k_n (k_{n}-1)s^2}{(n-1)^2}\bigg) \nonumber \\ & \leq {6}(s+1)^2\textrm{e}^{-x}\frac{(\alpha\log n+x)^2}{n^{1+\alpha}} \leq c_2(x) \frac{s^2\alpha^2 \log(n)^2}{n^{1+\alpha}}.\end{align}
\begin{align} T_1 & \leq \bigg(1-\frac{s}{n}\bigg)^{k_n}\frac{n}{(n-s)^2} \bigg(\frac{k_n s}{n-1} + \frac{k_n (k_{n}-1)s^2}{(n-1)^2}\bigg) \nonumber \\ & \leq {6}(s+1)^2\textrm{e}^{-x}\frac{(\alpha\log n+x)^2}{n^{1+\alpha}} \leq c_2(x) \frac{s^2\alpha^2 \log(n)^2}{n^{1+\alpha}}.\end{align}
To deal with the term
![]() $T_2$
, first note that, by (4) and (5),
$T_2$
, first note that, by (4) and (5),
 \begin{align} \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I}\Big] & = \mathbb{P}(E_{n,j}(k_n)) \mathbb{P}\big( F_{n,j}^I \mid E_{n,j}(k_n)\big) \notag \\ & = \mathbb{P}(E_{n,j}(k_n)) \sum_{\ell=0}^{k_n} \mathbb{P}\big( F_{n,j}^I \mid E_{n,j}(k_n) \cap \{\vert C_I \vert = \ell\} \big) \mathbb{P}\big(\vert C_I \vert = \ell \mid E_{n,j}(k_n)\big) \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \sum_{\ell=0}^{k_n} \bigg(1-\bigg(1-\frac{1}{n-s}\bigg)^\ell\bigg) \left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(\frac{s}{n-1}\bigg)^\ell \bigg(1-\frac{s}{n-1}\bigg)^{k_n -\ell} \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \Bigg(1 - \sum_{\ell=0}^{k_n}\bigg(1-\frac{1}{n-s}\bigg)^\ell \left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(\frac{s}{n-1}\bigg)^\ell \bigg(1-\frac{s}{n-1}\bigg)^{k_n -\ell}\Bigg) \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \bigg(1-\bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{k_n}\bigg).\end{align}
\begin{align} \mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I}\Big] & = \mathbb{P}(E_{n,j}(k_n)) \mathbb{P}\big( F_{n,j}^I \mid E_{n,j}(k_n)\big) \notag \\ & = \mathbb{P}(E_{n,j}(k_n)) \sum_{\ell=0}^{k_n} \mathbb{P}\big( F_{n,j}^I \mid E_{n,j}(k_n) \cap \{\vert C_I \vert = \ell\} \big) \mathbb{P}\big(\vert C_I \vert = \ell \mid E_{n,j}(k_n)\big) \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \sum_{\ell=0}^{k_n} \bigg(1-\bigg(1-\frac{1}{n-s}\bigg)^\ell\bigg) \left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(\frac{s}{n-1}\bigg)^\ell \bigg(1-\frac{s}{n-1}\bigg)^{k_n -\ell} \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \Bigg(1 - \sum_{\ell=0}^{k_n}\bigg(1-\frac{1}{n-s}\bigg)^\ell \left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(\frac{s}{n-1}\bigg)^\ell \bigg(1-\frac{s}{n-1}\bigg)^{k_n -\ell}\Bigg) \notag \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n} \bigg(1-\bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{k_n}\bigg).\end{align}
Using (14) and slightly adapting (5), the first part of
![]() $T_2$
can be handled in the following way:
$T_2$
can be handled in the following way:
 \begin{align*} & \mathbb{E}\Big[\mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big] \, \mathbb{E}\Big[\mathbf{1}_{E_{n,i}(k_n)\cap F_{n,i}^I} \mid \mathcal{C}_n(k_n) \Big]\Big] \\ & = \mathbb{E}\bigg[\mathbf{1}_{E_{n,i}(k_n)}\mathbf{1}_{E_{n,j}(k_n)} \bigg(1 - \bigg(1-\frac{1}{n-s}\bigg)^{\vert C_I\vert}\bigg)^2\bigg] \\ & = \sum_{\ell=0}^{k_n}\bigg(1 - \bigg(1-\frac{1}{n-s}\bigg)^{\ell}\bigg)^2 \, \mathbb{P}(\vert C_I\vert = \ell \mid E_{n,i}(k_n) \cap E_{n,j}(k_n))\, \mathbb{P}(E_{n,i}(k_n)\cap E_{n,j}(k_n)) \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(1-\frac{s}{n-1}\bigg)^{k_n} \sum_{\ell=0}^{k_n}\bigg(1 - \bigg(1-\frac{1}{n-s}\bigg)^{\ell}\bigg)^2 \, \left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(\frac{s}{n-2}\bigg)^\ell \bigg(1-\frac{s}{n-2}\bigg)^{k_n -\ell} \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(1-\frac{s}{n-1}\bigg)^{k_n} \\ & \quad \times \sum_{\ell=0}^{k_n}\bigg(1-2\bigg(1-\frac{1}{n-s}\bigg)^{\ell} + \bigg(1-\frac{1}{n-s}\bigg)^{2\ell}\bigg)\,\left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(\frac{s}{n-2}\bigg)^\ell \bigg(1-\frac{s}{n-2}\bigg)^{k_n -\ell} \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(1-\frac{s}{n-1}\bigg)^{k_n} \\ & \quad \times \bigg(1 - 2\bigg(1-\frac{s}{(n-2)(n-s)}\bigg)^{k_n} + \bigg(1-\frac{2s}{(n-2)(n-s)} + \frac{s}{(n-2)(n-s)^2}\bigg)^{k_n}\bigg),\end{align*}
\begin{align*} & \mathbb{E}\Big[\mathbb{E}\Big[\mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mid \mathcal{C}_n(k_n) \Big] \, \mathbb{E}\Big[\mathbf{1}_{E_{n,i}(k_n)\cap F_{n,i}^I} \mid \mathcal{C}_n(k_n) \Big]\Big] \\ & = \mathbb{E}\bigg[\mathbf{1}_{E_{n,i}(k_n)}\mathbf{1}_{E_{n,j}(k_n)} \bigg(1 - \bigg(1-\frac{1}{n-s}\bigg)^{\vert C_I\vert}\bigg)^2\bigg] \\ & = \sum_{\ell=0}^{k_n}\bigg(1 - \bigg(1-\frac{1}{n-s}\bigg)^{\ell}\bigg)^2 \, \mathbb{P}(\vert C_I\vert = \ell \mid E_{n,i}(k_n) \cap E_{n,j}(k_n))\, \mathbb{P}(E_{n,i}(k_n)\cap E_{n,j}(k_n)) \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(1-\frac{s}{n-1}\bigg)^{k_n} \sum_{\ell=0}^{k_n}\bigg(1 - \bigg(1-\frac{1}{n-s}\bigg)^{\ell}\bigg)^2 \, \left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(\frac{s}{n-2}\bigg)^\ell \bigg(1-\frac{s}{n-2}\bigg)^{k_n -\ell} \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(1-\frac{s}{n-1}\bigg)^{k_n} \\ & \quad \times \sum_{\ell=0}^{k_n}\bigg(1-2\bigg(1-\frac{1}{n-s}\bigg)^{\ell} + \bigg(1-\frac{1}{n-s}\bigg)^{2\ell}\bigg)\,\left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(\frac{s}{n-2}\bigg)^\ell \bigg(1-\frac{s}{n-2}\bigg)^{k_n -\ell} \\ & = \bigg(1-\frac{s}{n}\bigg)^{k_n}\bigg(1-\frac{s}{n-1}\bigg)^{k_n} \\ & \quad \times \bigg(1 - 2\bigg(1-\frac{s}{(n-2)(n-s)}\bigg)^{k_n} + \bigg(1-\frac{2s}{(n-2)(n-s)} + \frac{s}{(n-2)(n-s)^2}\bigg)^{k_n}\bigg),\end{align*}
independently of i and j. Combining this with (16) yields
 \begin{align*} T_2 & \leq n^2 \bigg(1-\frac{s}{n}\bigg)^{2k_n} \bigg[2\bigg(\bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{k_n} - \bigg(1-\frac{s}{(n-s)(n-2)}\bigg)^{k_n}\bigg) \\ & \quad + \bigg(1 - \frac{2s}{(n-s)(n-2)} + \frac{s}{(n-2)(n-s)^2}\bigg)^{k_n} - \bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{2k_n}\bigg].\end{align*}
\begin{align*} T_2 & \leq n^2 \bigg(1-\frac{s}{n}\bigg)^{2k_n} \bigg[2\bigg(\bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{k_n} - \bigg(1-\frac{s}{(n-s)(n-2)}\bigg)^{k_n}\bigg) \\ & \quad + \bigg(1 - \frac{2s}{(n-s)(n-2)} + \frac{s}{(n-2)(n-s)^2}\bigg)^{k_n} - \bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{2k_n}\bigg].\end{align*}
Now, there exists
![]() $n_2=n_2(\alpha,s)$
such that, for all
$n_2=n_2(\alpha,s)$
such that, for all
![]() $n\geq n_2$
,
$n\geq n_2$
,
 \begin{align*} \bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{k_n} - \bigg(1-\frac{s}{(n-s)(n-2)}\bigg)^{k_n} & \leq 2 \frac{\alpha \log(n)+x}{n^2}, \\ \bigg(1 - \frac{2s}{(n-s)(n-2)} + \frac{s}{(n-2)(n-s)^2}\bigg)^{k_n} - \bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{2k_n} & \leq 2 \frac{\alpha \log(n)+x}{n^2}.\end{align*}
\begin{align*} \bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{k_n} - \bigg(1-\frac{s}{(n-s)(n-2)}\bigg)^{k_n} & \leq 2 \frac{\alpha \log(n)+x}{n^2}, \\ \bigg(1 - \frac{2s}{(n-s)(n-2)} + \frac{s}{(n-2)(n-s)^2}\bigg)^{k_n} - \bigg(1-\frac{s}{(n-s)(n-1)}\bigg)^{2k_n} & \leq 2 \frac{\alpha \log(n)+x}{n^2}.\end{align*}
Combining this with (8) we can conclude that there exists a constant
![]() ${c_3(x)} \in (0, \infty)$
such that, for all
${c_3(x)} \in (0, \infty)$
such that, for all
![]() $n \geq \max\{3,n_2\}$
,
$n \geq \max\{3,n_2\}$
,
Putting the bounds in (15) and (17) into (13), we see that there exists a constant
![]() ${c_4(x)} \in (0, \infty)$
such that, for all
${c_4(x)} \in (0, \infty)$
such that, for all
![]() $n \geq \max\{3,n_2\}$
,
$n \geq \max\{3,n_2\}$
,
 \begin{align} \textrm{var}\big(\mathbb{E}\big[Z_{n,s}-Z^I_{n,s}\mid\mathcal{C}_n(k_n) \big]\big) & \leq c_2(x) \frac{s^2\alpha^2 \log(n)^2}{n^{1+\alpha}} + c_3(x)\frac{\alpha \log(n)}{n^{2 \alpha}} \nonumber \\ & \leq c_4(x)\bigg(\frac{s^2\alpha^2 \log(n)^2}{n^{1+\alpha}} + \frac{\alpha \log(n)}{n^{2 \alpha}}\bigg). \end{align}
\begin{align} \textrm{var}\big(\mathbb{E}\big[Z_{n,s}-Z^I_{n,s}\mid\mathcal{C}_n(k_n) \big]\big) & \leq c_2(x) \frac{s^2\alpha^2 \log(n)^2}{n^{1+\alpha}} + c_3(x)\frac{\alpha \log(n)}{n^{2 \alpha}} \nonumber \\ & \leq c_4(x)\bigg(\frac{s^2\alpha^2 \log(n)^2}{n^{1+\alpha}} + \frac{\alpha \log(n)}{n^{2 \alpha}}\bigg). \end{align}
Remark 4. Using (13) and the exact expressions for the probabilities appearing there, it can be shown that for constant s the order of (18) is optimal, in the sense that we can find constants
![]() $c,C\in(0,\infty)$
only depending on s and x such that
$c,C\in(0,\infty)$
only depending on s and x such that
for sufficiently large n.
4.3. Bounding
 $\mathbb{E}\big[\big(Z_{n,s}-Z^I_{n,s}\big)^2\big]$
$\mathbb{E}\big[\big(Z_{n,s}-Z^I_{n,s}\big)^2\big]$
For the second term in (7) it remains to bound
![]() $\mathbb{E}\big[\big(Z_{n,s}-Z^I_{n,s}\big)^2\big]$
. We have
$\mathbb{E}\big[\big(Z_{n,s}-Z^I_{n,s}\big)^2\big]$
. We have
 \begin{align} \mathbb{E}\big[\big(Z_{n,s}-Z^I_{n,s}\big)^2\big] & \leq \mathbb{E}\Bigg[\Bigg(\sum_{\substack{j=1\\ j \neq I}}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} - 1\Bigg)^2\Bigg] \notag \\ & = \mathbb{E}\Bigg[\Bigg(\sum_{\substack{j=1\\ j \neq I}}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I}\Bigg)^2\Bigg] - 2\mathbb{E}\Bigg[\sum_{\substack{j=1\\ j \neq I}}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}}\Bigg] + 1 \notag \\ & \leq \mathbb{E}\Bigg[\sum_{\substack{j=1\\ j \neq I}}^n \sum_{\substack{i=1 \\ i\neq j,I}}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mathbf{1}_{E_{n,i}(k_n)\cap F_{n,i}^I}\Bigg] + 1,\end{align}
\begin{align} \mathbb{E}\big[\big(Z_{n,s}-Z^I_{n,s}\big)^2\big] & \leq \mathbb{E}\Bigg[\Bigg(\sum_{\substack{j=1\\ j \neq I}}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} - 1\Bigg)^2\Bigg] \notag \\ & = \mathbb{E}\Bigg[\Bigg(\sum_{\substack{j=1\\ j \neq I}}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I}\Bigg)^2\Bigg] - 2\mathbb{E}\Bigg[\sum_{\substack{j=1\\ j \neq I}}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}}\Bigg] + 1 \notag \\ & \leq \mathbb{E}\Bigg[\sum_{\substack{j=1\\ j \neq I}}^n \sum_{\substack{i=1 \\ i\neq j,I}}^n \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mathbf{1}_{E_{n,i}(k_n)\cap F_{n,i}^I}\Bigg] + 1,\end{align}
where the
![]() $-1$
in the first line comes from the artificially isolated cell with index I. For the first sum, note that
$-1$
in the first line comes from the artificially isolated cell with index I. For the first sum, note that
where
![]() $\mathbb{P}(E_{n,j}(k_n)\cap E_{n,j}(k_n))$
can be bounded using (6) and (8). To bound the remaining probability, we observe that, similarly to the considerations in (16), we have
$\mathbb{P}(E_{n,j}(k_n)\cap E_{n,j}(k_n))$
can be bounded using (6) and (8). To bound the remaining probability, we observe that, similarly to the considerations in (16), we have
 \begin{align*} \mathbb{P}\big(F_{n,j}^I & \mid E_{n,i}(k_n) \cap E_{n,j}(k_n)\big) \\ & = \sum_{\ell=0}^{k_n} \mathbb{P}\big(F_{n,j}^I \mid E_{n,i}(k_n)\cap E_{n,j}(k_n)\cap\{|C_I|=\ell\}\big) \mathbb{P}\big(|C_I|=\ell \mid E_{n,i}(k_n)\cap E_{n,j}(k_n)\big) \\ & = \sum_{\ell=0}^{k_n} \left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(1-\bigg(1-\frac{1}{n-s}\bigg)^\ell\bigg) \bigg(\frac{s}{n-2}\bigg)^\ell\bigg(1-\frac{s}{n-2}\bigg)^{k_n-\ell} \\ & = 1 - \bigg(1-\frac{s}{(n-2)(n-s)}\bigg)^{k_n},\end{align*}
\begin{align*} \mathbb{P}\big(F_{n,j}^I & \mid E_{n,i}(k_n) \cap E_{n,j}(k_n)\big) \\ & = \sum_{\ell=0}^{k_n} \mathbb{P}\big(F_{n,j}^I \mid E_{n,i}(k_n)\cap E_{n,j}(k_n)\cap\{|C_I|=\ell\}\big) \mathbb{P}\big(|C_I|=\ell \mid E_{n,i}(k_n)\cap E_{n,j}(k_n)\big) \\ & = \sum_{\ell=0}^{k_n} \left(\begin{array}{c}k_n\\\ell\end{array}\right) \bigg(1-\bigg(1-\frac{1}{n-s}\bigg)^\ell\bigg) \bigg(\frac{s}{n-2}\bigg)^\ell\bigg(1-\frac{s}{n-2}\bigg)^{k_n-\ell} \\ & = 1 - \bigg(1-\frac{s}{(n-2)(n-s)}\bigg)^{k_n},\end{align*}
independently of the choice of i and j. So, we are left to deal with
![]() $\mathbb{P}\big(F_{n,i}^I \mid E_{n,i}(k_n)\cap E_{n,j}(k_n)\cap F_{n,j}^I\big)$
. For
$\mathbb{P}\big(F_{n,i}^I \mid E_{n,i}(k_n)\cap E_{n,j}(k_n)\cap F_{n,j}^I\big)$
. For
![]() $i \neq j$
,
$i \neq j$
,
since the event
![]() $F_{n,j}^I$
implies that at least one particle from cell I is placed into cell
$F_{n,j}^I$
implies that at least one particle from cell I is placed into cell
![]() $C_j$
, reducing the chances of cell
$C_j$
, reducing the chances of cell
![]() $C_i$
receiving a particle. Hence,
$C_i$
receiving a particle. Hence,
and we finally obtain, for
![]() $n \geq s$
,
$n \geq s$
,
 \begin{align*} \mathbb{E}\Bigg[\sum_{\substack{j=1\\ j\neq I}}^n \sum_{\substack{i=1 \\ i\neq j,I}}^n & \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mathbf{1}_{E_{n,i}(k_n)\cap F_{n,i}^I}\Bigg] \\ & = \sum_{\substack{j=1\\ j\neq I}}^n \sum_{\substack{i=1 \\ i\neq j, I}}^n \mathbb{P}\big(F_{n,i}^I \cap F_{n,j}^I \mid E_{n,i}(k_n) \cap E_{n,j}(k_n)\big) \mathbb{P}(E_{n,i}(k_n) \cap E_{n,j}(k_n)) \\ & \leq (n-1)(n-2) \bigg(1 - \bigg(1-\frac{s}{(n-2)(n-s)}\bigg)^{k_n}\bigg)^2 \bigg(1-\frac{s}{n}\bigg)^{2k_n} \\ & \leq (n-1)(n-2) \bigg(k_n \frac{s}{(n-2)(n-s)}\bigg)^2 \bigg(1-\frac{s}{n}\bigg)^{2k_n} \\ & \leq (n-1)(n-2)\bigg(\frac{3 (s+1)(\alpha \log(n)+x)}{n}\bigg)^2 \bigg(\frac{\textrm{e}^{-x}\alpha\log(n)}{n^{\alpha}}\bigg)^2 \\ & \leq {9}(s+1)^2 \textrm{e}^{-2x}\frac{(\alpha\log(n)+x)^2{ \alpha^2 \log(n)^2}}{n^{2 \alpha}},\end{align*}
\begin{align*} \mathbb{E}\Bigg[\sum_{\substack{j=1\\ j\neq I}}^n \sum_{\substack{i=1 \\ i\neq j,I}}^n & \mathbf{1}_{E_{n,j}(k_n)\cap F_{n,j}^I} \mathbf{1}_{E_{n,i}(k_n)\cap F_{n,i}^I}\Bigg] \\ & = \sum_{\substack{j=1\\ j\neq I}}^n \sum_{\substack{i=1 \\ i\neq j, I}}^n \mathbb{P}\big(F_{n,i}^I \cap F_{n,j}^I \mid E_{n,i}(k_n) \cap E_{n,j}(k_n)\big) \mathbb{P}(E_{n,i}(k_n) \cap E_{n,j}(k_n)) \\ & \leq (n-1)(n-2) \bigg(1 - \bigg(1-\frac{s}{(n-2)(n-s)}\bigg)^{k_n}\bigg)^2 \bigg(1-\frac{s}{n}\bigg)^{2k_n} \\ & \leq (n-1)(n-2) \bigg(k_n \frac{s}{(n-2)(n-s)}\bigg)^2 \bigg(1-\frac{s}{n}\bigg)^{2k_n} \\ & \leq (n-1)(n-2)\bigg(\frac{3 (s+1)(\alpha \log(n)+x)}{n}\bigg)^2 \bigg(\frac{\textrm{e}^{-x}\alpha\log(n)}{n^{\alpha}}\bigg)^2 \\ & \leq {9}(s+1)^2 \textrm{e}^{-2x}\frac{(\alpha\log(n)+x)^2{ \alpha^2 \log(n)^2}}{n^{2 \alpha}},\end{align*}
where we used (11) to arrive at the third line. Plugging this back into (19), we conclude that there exists a constant
![]() ${c_5(x)}\in (0, \infty)$
such that, for all
${c_5(x)}\in (0, \infty)$
such that, for all
![]() $n \geq s$
,
$n \geq s$
,
Combining the normal approximation bound (7) with the estimates (9), (12), (18), and (20), we arrive at
 \begin{align*} d_{\textrm{W}}\big(\tilde{Z}_{n,s},G\big) &\leq \frac{\lambda_n}{c_1(x)\lambda_n}\sqrt{c_4(x)\bigg(\frac{s^2\alpha^2 \log(n)^2}{n^{1+\alpha}} + \frac{\alpha \log(n)}{n^{2 \alpha}}\bigg)} + \frac{\lambda_n}{(c_1(x)\lambda_n)^{{3}/{2}}}c_5(x)s^2 \\ & \leq \frac{\sqrt{c_4(x)}\,\alpha}{c_1(x)}\frac{s\log n}{n^{(1+\alpha)/2}} + \frac{{\sqrt{c_4(x)}}\sqrt{\alpha}}{c_1(x)}\frac{\sqrt{\log(n)}}{n^{\alpha}} + \frac{c_5(x)}{c_1(x)^{3/2}}\frac{{\sqrt{2}}s^2}{n^{(1-\alpha)/2}{\textrm{e}^{-{x}/{2}}}} \\ & \leq C\bigg(\frac{\sqrt{\log(n)}}{n^{\alpha}}+\frac{s^2}{n^{(1-\alpha)/2}}\bigg)\end{align*}
\begin{align*} d_{\textrm{W}}\big(\tilde{Z}_{n,s},G\big) &\leq \frac{\lambda_n}{c_1(x)\lambda_n}\sqrt{c_4(x)\bigg(\frac{s^2\alpha^2 \log(n)^2}{n^{1+\alpha}} + \frac{\alpha \log(n)}{n^{2 \alpha}}\bigg)} + \frac{\lambda_n}{(c_1(x)\lambda_n)^{{3}/{2}}}c_5(x)s^2 \\ & \leq \frac{\sqrt{c_4(x)}\,\alpha}{c_1(x)}\frac{s\log n}{n^{(1+\alpha)/2}} + \frac{{\sqrt{c_4(x)}}\sqrt{\alpha}}{c_1(x)}\frac{\sqrt{\log(n)}}{n^{\alpha}} + \frac{c_5(x)}{c_1(x)^{3/2}}\frac{{\sqrt{2}}s^2}{n^{(1-\alpha)/2}{\textrm{e}^{-{x}/{2}}}} \\ & \leq C\bigg(\frac{\sqrt{\log(n)}}{n^{\alpha}}+\frac{s^2}{n^{(1-\alpha)/2}}\bigg)\end{align*}
for some constant
![]() $C=C(x,\alpha)\in (0, \infty)$
and for all
$C=C(x,\alpha)\in (0, \infty)$
and for all
![]() $n \geq N \,:\!=\, \max\{n_1,n_2,3,s,\textrm{e}^{-x}\}$
. Here, we used that
$n \geq N \,:\!=\, \max\{n_1,n_2,3,s,\textrm{e}^{-x}\}$
. Here, we used that
![]() $\mathbb{E}[Z_{n,s}] \geq \frac{1}{2}\textrm{e}^{-x}n^{1-\alpha}$
for
$\mathbb{E}[Z_{n,s}] \geq \frac{1}{2}\textrm{e}^{-x}n^{1-\alpha}$
for
![]() $n\geq 2$
in the second step. Note that in the last step we also used that
$n\geq 2$
in the second step. Note that in the last step we also used that
which is equivalent to
![]() $\log n\leq sn^\alpha$
and thus automatically satisfied. This proves Theorem 1.
$\log n\leq sn^\alpha$
and thus automatically satisfied. This proves Theorem 1.
Remark 5. The constants C and N in Theorem 1 can be made fully explicit in terms of the parameters x and
![]() $\alpha$
. To see this, we start by noting that in (8) the asymptotic equivalence ‘
$\alpha$
. To see this, we start by noting that in (8) the asymptotic equivalence ‘
![]() $\sim$
’ can be replaced by ‘
$\sim$
’ can be replaced by ‘
![]() $\leq$
’, and that
$\leq$
’, and that
![]() $\mathbb{E}[Z_{n,s}] \geq \frac{1}{2}\textrm{e}^{-x}n^{1-\alpha}$
for
$\mathbb{E}[Z_{n,s}] \geq \frac{1}{2}\textrm{e}^{-x}n^{1-\alpha}$
for
![]() $n\geq 2$
. With this inequality we can conclude from the computations in Section 4.1 that
$n\geq 2$
. With this inequality we can conclude from the computations in Section 4.1 that
 \begin{align*} \frac{\lambda_n}{\sigma_n^2} & \leq \bigg(1-\frac{\textrm{e}^{-x}}{n^\alpha}-\frac{2\textrm{e}^{-x}(\alpha\log (n)+x)}{n^\alpha}\bigg)^{-1}, \\ \frac{\lambda_n}{\sigma_n^3} & \leq \bigg(1-\frac{e^{-x}}{n^\alpha}-\frac{2e^{-x}(\alpha\log (n)+x)}{n^\alpha}\bigg)^{-3/2} \bigg({\frac{1}{2}}\textrm{e}^{-x}n^{1-\alpha}\bigg)^{-1/2}. \end{align*}
\begin{align*} \frac{\lambda_n}{\sigma_n^2} & \leq \bigg(1-\frac{\textrm{e}^{-x}}{n^\alpha}-\frac{2\textrm{e}^{-x}(\alpha\log (n)+x)}{n^\alpha}\bigg)^{-1}, \\ \frac{\lambda_n}{\sigma_n^3} & \leq \bigg(1-\frac{e^{-x}}{n^\alpha}-\frac{2e^{-x}(\alpha\log (n)+x)}{n^\alpha}\bigg)^{-3/2} \bigg({\frac{1}{2}}\textrm{e}^{-x}n^{1-\alpha}\bigg)^{-1/2}. \end{align*}
Furthermore, an inspection of Sections 4.2 and 4.3 shows that
 \begin{align*} \textrm{var}\big(\mathbb{E}\big[Z_{n,s}-Z^I_{n,s}\mid\mathcal{C}_n(k_n)\big]\big) & \leq {6}(s+1)^2\textrm{e}^{-x}\frac{(\alpha\log (n)+x)^2}{n^{1+\alpha}} + 4\textrm{e}^{-2x}\frac{\alpha\log (n)+x}{n^{2\alpha}}, \\ \mathbb{E}\big[\big(Z_{n,s}-Z^I_{n,s}\big)^2\big] & \leq 9(s+1)^2\textrm{e}^{-2x}\frac{(\alpha\log (n)+{x})^2{\alpha^2 \log(n)^2}}{n^{2\alpha}}+1, \end{align*}
\begin{align*} \textrm{var}\big(\mathbb{E}\big[Z_{n,s}-Z^I_{n,s}\mid\mathcal{C}_n(k_n)\big]\big) & \leq {6}(s+1)^2\textrm{e}^{-x}\frac{(\alpha\log (n)+x)^2}{n^{1+\alpha}} + 4\textrm{e}^{-2x}\frac{\alpha\log (n)+x}{n^{2\alpha}}, \\ \mathbb{E}\big[\big(Z_{n,s}-Z^I_{n,s}\big)^2\big] & \leq 9(s+1)^2\textrm{e}^{-2x}\frac{(\alpha\log (n)+{x})^2{\alpha^2 \log(n)^2}}{n^{2\alpha}}+1, \end{align*}
which in view of (7) leads to a fully explicit error bound (which is valid whenever the resulting expression is positive). In particular, the dependence of this bound on the parameters s, x,
![]() $\alpha$
, and n can be studied as demonstrated in Fig. 3 (note that in contrast to the Kolmogorov distance, which is bounded by 1, the Wasserstein distance can take arbitrarily large values).
$\alpha$
, and n can be studied as demonstrated in Fig. 3 (note that in contrast to the Kolmogorov distance, which is bounded by 1, the Wasserstein distance can take arbitrarily large values).

Figure 3. Dependence of the normal approximation bound on the parameters
![]() $\alpha$
, x, s, and n. Top left:
$\alpha$
, x, s, and n. Top left:
![]() $\alpha\in\big[\frac13,1\big)$
, while
$\alpha\in\big[\frac13,1\big)$
, while
![]() $x=0$
,
$x=0$
,
![]() $s=5$
,
$s=5$
,
![]() $n=1000$
. Top right:
$n=1000$
. Top right:
![]() $x\in[0,10]$
, while
$x\in[0,10]$
, while
![]() $\alpha=\frac12$
,
$\alpha=\frac12$
,
![]() $s=5$
,
$s=5$
,
![]() $n=1000$
. Bottom left:
$n=1000$
. Bottom left:
![]() $s\in\{1,\ldots,10\}$
, while
$s\in\{1,\ldots,10\}$
, while
![]() $\alpha=\frac12$
,
$\alpha=\frac12$
,
![]() $x=0$
,
$x=0$
,
![]() $n=1000$
. Bottom right:
$n=1000$
. Bottom right:
![]() $n\in\{1000,\ldots,10\,000\}$
, while
$n\in\{1000,\ldots,10\,000\}$
, while
![]() $\alpha=\frac12$
,
$\alpha=\frac12$
,
![]() $x=0$
,
$x=0$
,
![]() $s=5$
.
$s=5$
.
5. Proof of Theorem 2
As already mentioned in the introduction, rates of convergence towards a Poisson limit in the case
![]() $\alpha=1$
can be concluded from [Reference Barbour, Holst and Janson2, Theorem 6.F]. Nevertheless, we give an alternative self-contained proof using the coupling from Section 3.
$\alpha=1$
can be concluded from [Reference Barbour, Holst and Janson2, Theorem 6.F]. Nevertheless, we give an alternative self-contained proof using the coupling from Section 3.
Proof of Theorem
2.It follows from [Reference Ross15, Theorem 4.13] that the total variation distance between the number of empty cells in the coupon collector’s problem and a Poisson random variable W with parameter
![]() $\lambda_n=\mathbb{E}[Z_{n,s}(k_n)]$
can be bounded using the following inequality:
$\lambda_n=\mathbb{E}[Z_{n,s}(k_n)]$
can be bounded using the following inequality:
For the expectation on the right, the definitions of
![]() $Z_{n,s}(k_n)$
and
$Z_{n,s}(k_n)$
and
![]() $Z^I_{n,s}(k_n)$
yield
$Z^I_{n,s}(k_n)$
yield
 \begin{align*} \mathbb{E}\big[Z_{n,s}(k_n)+1-Z_{n,s}^I(k_n)\big] & = \mathbb{E}[\mathbf{1}_{E_{n,I}(k_n)}] + \mathbb{E}\Bigg[\sum_{j\neq I} \mathbf{1}_{E_{n,j}(k_n)} - \mathbf{1}_{E^I_{n,j}(k_n)}\Bigg] \\ & = \bigg(1-\frac{s}{n}\bigg)^k + (n-1)\bigg(\bigg(1-\frac{s}{n}\bigg)^k - \bigg(1-\frac{s}{n-1}\bigg)^k \bigg). \end{align*}
\begin{align*} \mathbb{E}\big[Z_{n,s}(k_n)+1-Z_{n,s}^I(k_n)\big] & = \mathbb{E}[\mathbf{1}_{E_{n,I}(k_n)}] + \mathbb{E}\Bigg[\sum_{j\neq I} \mathbf{1}_{E_{n,j}(k_n)} - \mathbf{1}_{E^I_{n,j}(k_n)}\Bigg] \\ & = \bigg(1-\frac{s}{n}\bigg)^k + (n-1)\bigg(\bigg(1-\frac{s}{n}\bigg)^k - \bigg(1-\frac{s}{n-1}\bigg)^k \bigg). \end{align*}
Combining (8) and (10) for
![]() $\alpha =1$
with (21) yields
$\alpha =1$
with (21) yields
 \begin{align*} d_\textrm{TV}(Z_{n,s}(k_n), W) & \leq \min\{1, \lambda_n\} \, \mathbb{E}\big[Z_{n,s}(k_n)+1-Z_{n,s}^I(k_n)\big] \\ & = \bigg(1-\frac{s}{n}\bigg)^k + (n-1)\bigg(\bigg(1-\frac{s}{n}\bigg)^k - \bigg(1-\frac{s}{n-1}\bigg)^k \bigg) \\ & \leq \frac{\textrm{e}^{-x}}{n}({\log}(n)+x+1) \end{align*}
\begin{align*} d_\textrm{TV}(Z_{n,s}(k_n), W) & \leq \min\{1, \lambda_n\} \, \mathbb{E}\big[Z_{n,s}(k_n)+1-Z_{n,s}^I(k_n)\big] \\ & = \bigg(1-\frac{s}{n}\bigg)^k + (n-1)\bigg(\bigg(1-\frac{s}{n}\bigg)^k - \bigg(1-\frac{s}{n-1}\bigg)^k \bigg) \\ & \leq \frac{\textrm{e}^{-x}}{n}({\log}(n)+x+1) \end{align*}
for
![]() $n \geq \tilde{N}\,:\!=\,\max\big\{ n_1, \textrm{e}^{-(x+1)}\big\}$
, which completes the proof of Theorem 2.
$n \geq \tilde{N}\,:\!=\,\max\big\{ n_1, \textrm{e}^{-(x+1)}\big\}$
, which completes the proof of Theorem 2.
Acknowledgements
The authors would like to thank Chinmoy Bhattacharjee for pointing us to the paper of Englund [Reference Englund5]. Moreover, we would like to thank two anonymous referees for helping us to improve our text.
Funding information
This work has been supported by the DFG priority program SPP 2265 Random Geometric Systems.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.