As president of the organizing committee of this meeting I was granted the honor of opening the conference. But despite appearances I was only a figurehead that Jean-Paul Zahn somehow decided to set up. Whatever his motivation was, his execution was excellent and my first remark must be an expression of my admiration for the marvelous job that he and his associates have done in providing all the spiritual, intellectual, and material advantages that we found waiting for us in Nice. Let me assure you though, that a token president is not without uses and I wish I had known this before accepting the job. I spent the days before and during the conference running routine errands, carrying luggage, and being reprimanded for some of the minor things that inevitably must go wrong in many large gatherings. I was even scolded because the name of someone who had not said he was coming was omitted from the list of participants. And when the time was running short during the meeting, I was obliged, in a statesmanlike gesture, to cut my scheduled one-hour talk to eight minutes. But rank has its privileges and mine was to be informed of the guiding principles behind the organization of the conference. Permit me now to share these with you.

To set the stage for the report to follow, let me start with a quotation from A.S. Eddington's classical work “The Internal Constitution of the Stars”, published exactly half a century ago. Eddington wrote: “We shall not enter further into the historic problem of convective equilibrium since modern researches show that the hypothesis is untenable. In stellar conditions the main process of transfer of heat is by radiation and other modes of transfer may be neglected.” (paragraph 69, p. 98).

The basic assumptions of the mixing-length formalism are described, and the theory is developed with a view to representing convection in stars. Directions in which the results might be improved and extended are indicated.

There has been progress in convection theory in the past decade, mainly in the problem of mild convection. Yet, we are still not able to cope with vigorous convection such as we face in the envelopes of late-type stars. Most astrophysicists therefore use mixing-length theory and get on with calculating their models. As this situation may continue for a while, it may be a good thing to consider what mixing-length theory really is and to see whether it can be taken seriously as a physical model for stellar convection.

It is shown that the best way to get information about efficiency of convective energy transport in the hydrogen convection zones in stars other than the sun is presently contained in continuous energy distributions of A and F stars. Scans show that convective energy transport must be much more efficient than thought hitherto. The scans indicate that rapid rotation enhances convective energy transport.

Figure 1 lists all the observations, we could think of, which are influenced by the outer convection zone and which can therefore give us information for our convection theory.

The linear dynamical instability at the origin of convection in stars is reviewed and shown to depend essentially on the sign of 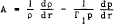which is the usual argument of convection criteria. The case of two or more superadiabatic regions separated by subadiabatic ones might well deserve more detailed attention.

Once this instability is partially removed by the setting in of convection its effects must be balanced by dissipation terms if a stationary state is to result. This yields the value of a Rayleigh number.

If energy generation is included in the non-conservative terms, possibilities are somewhat enriched including a case of dynamical instability in presence of A<0 (usually stable) but very small in absolute value.

• 1. Solar observations contain a considerable amount of information on the hydrodynamics of stellar convection. We emphasize and discuss especially

• (a)the existence of two very different cell sizes,

• (b) the unexpectedly high cross-correlation between vertical velocities and temperature fluctuations in the granulation,

• (c) the fast "downdrafts" in intergranular regions,

• (d) the existence of cells much larger than the scale height,

• (e) the strange behavior of the temperature fluctuations in the supergranulation, and

• (f) the importance of convective overshoot.

• 2. The Li-Be problem and its possible relevance as an indicator of convective overshoot is briefly summarized.

• 3. Convection may have a stronger influence on the observable properties of Herich (“non-DA”) white dwarfs than of most other stars. We discuss especially

• (a) the persistence of outer convection zones through a very wide range of effective temperatures,

• (b) the occurence of convection in high layers of the atmosphere,

• (c) the relatively high efficiency of convection in white dwarf atmospheres, and

• (d) the relevance of convection to the cooling problem.

The evolution pattern of the so-called exploding granules has been studied on the basis of a time sequence from Princeton Stratoscope pictures of the solar granulation. Some preliminary results are presented (section3). A new interpretation of the phenomenon is suggested (section 4).

The analysis of high resolution spectrograms that were obtained in Capri with the Coude refractor gave the following results regarding the granular fields.

• a) The rms velocity of the granulation was 300 m/sec. This value represents the raw data and should be substantially increased to account for instrumental and seeing effects (W. Mattig et al., 1969). Note that the oscillatory component of the total velocity field has been eliminated by a numerical filter.

• b) In the photosphere the intensity and velocity fluctuations show a similar structure. The size distributions of the observed Doppler shifts and intensity variations have been studied by means of power spectrum analysis (Fig.l, W. Mattig and A. Nesis, 1974). These spectra are not corrected for finite instrumental resolution or for atmospheric seeing.

Various aspects of convection in meteorology which may have some relevance for astrophysics are discussed. In particular the role of convection in determining the gross thermal structure of the atmosphere, the treatment of convective turbulence in the boundary layer, and the larger scale organization of convection are dealt with.

Two and three-dimensional computations have enlarged our understanding of nonlinear convection, particularly in Boussinesq fluids. However, we cannot adequately predict the relationship between convective heat transport and the superadiabatic temperature gradient. Nor is there any indication of a preferred length scale, other than the depth of the convecting layer, in a compressible fluid.

Stellar convection zones often extend over several pressure scale heights and convective velocities can be comparable to the local sound speed. Neither laboratory convection experimentsnor analytic solution of the non-linear equations are feasible in such regimes. In order to gain insight into the details of stellar convection we are obliged to use numerical simulations. At the present time, even this approach cannot be applied to the parameter range typical of stellar interiors; however solutions can be obtained which extend over many scale heights and have non-negligible Mach numbers. Under these conditions it is necessary to employ the full compressible equations rather than the anelastic approximation (Gough [l]) or the Boussinesq approximation (Spiegel & Veronis [2]).

It is shown that many features of convection in rotating spheres and spherical shells can be understood on the basis Of plane layer models. The phenomenon of differential rotation generated by convection is emphasized. The potential applications and limitations of analytical and numerical models for problems of astrophysical interest are briefly discussed.

In a highly conducting plasma convection is hindered by the imposition of a magnetic field. Convection may set in as direct or overstable modes and behaviour near the onset of instability depends on the ratio of the magnetic to the thermal diffusivity. Vigorous convection produces local flux concentrations with magnetic fields that may be much greater than the equipartition value. The interaction between magnetic fields and convection can be observed in detail on the sun and is essential to any stellar dynamo.

The non-linear Boussinesq equations describing axisymmetric convection in a cylinder with an initially uniform magnetic field have been integrated forward in time numerically. When the field is weak a strong central fluxrope is formed at the axis. In this case the maximum field strength can be limited either kinematically or by dynamical effects, and the equipartition prediction Bmax2 ∿ 4πμρu2 is easily exceeded. If the field is strong oscillations can occur and hysteresis is possible as the field is increased and decreased.

Convective dynamo theory can be regarded as combining two kinds of physical problems, each Involving an electrically conducting fluid medium, but differing in the role of the magnetic field and in the physical processes described. On the one hand, if the fluid is taken to be permeated by a prescribed magnetic field , under suitable conditions, involving a sufficiently strong flux of heat for example, convective motion of the fluid will ensue. On the other hand, kinematic dynamo theory insures that a sufficiently complicated fluid motion can sustain or excite a magnetic field.

Penetrative convection occurs in a fluid whenever a conyectively unstable region is bounded by a stable domain. This situation is encountered in many stars, and it is also a very common circumstance on Earth: in the oceans and in the atmosphere. One would therefore expect that the astrophysicists may largely benefit from the experience accumulated on this subject by the geophysicists.

It is worth noting that various definitions for the boundaries of a convective zone may be considered. Their importance for stellar evolution is very unequal.

The solar granulation, with its horizontal temperature fluctuations, and its associated velocity field, is a consequence of overshooting convective motions. Theoretical estimates of the magnitude of the temperature fluctuations and mass fluxes involved were obtained in a recent paper (Nordlund, 1976, Astronomy & Astrophys. 50, 23). Here, a simple model of the instantaneous granular velocity field is presented, and the effects of this velocity field on photospheric spectral lines are described.