No CrossRef data available.
Published online by Cambridge University Press: 12 April 2016
There have been several excellent reviews of observational helioseismology in recent years. These include the reviews by Harvey (1988), Libbrecht (1988), and van der Raay (1988) presented at a recent conference in Tenerife. The present effort will concentrate on the progress made on solar rotation recently.
The Sun is a resonant cavity that supports many (~ 107) modes of oscillation. The modes that are most easily observed are the acoustic or p-modes. The eigenfunctions for these modes are:
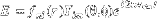
fnl(r) is the radial part of the separable eigenfunction where r is the radial coordinate measured from the center of the star. n is the number of radial nodes in the eigenfunction. Ylm (θ,ϕ) is the spherical harmonic function, where θ is the colatitude and ϕ is the longitude. The spherical harmonic degree l is the number of nodes of the spherical harmonic measured along a great circle that makes an angle 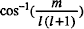 with the equator. The azimuthal order m is the number of nodes around the equator. The frequency of the eigenmode, vnlm, depends on the mode. Much of our information derived about the solar interior from helioseismology comes from the measurement of these frequencies.
with the equator. The azimuthal order m is the number of nodes around the equator. The frequency of the eigenmode, vnlm, depends on the mode. Much of our information derived about the solar interior from helioseismology comes from the measurement of these frequencies.