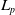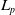1. Introduction
A central problem in classical harmonic analysis is finding conditions on symbols
![]() $\phi \in L_\infty ({\mathrm{\mathbb{R}}}^n)$
such that the associated Fourier multiplier
$\phi \in L_\infty ({\mathrm{\mathbb{R}}}^n)$
such that the associated Fourier multiplier
![]() $T_\phi$
is bounded on
$T_\phi$
is bounded on
![]() $L_p({\mathrm{\mathbb{R}}}^n)$
. One can replace
$L_p({\mathrm{\mathbb{R}}}^n)$
. One can replace
![]() ${\mathrm{\mathbb{R}}}^n$
here by any locally compact abelian group in a straightforward way. For non-abelian groups
${\mathrm{\mathbb{R}}}^n$
here by any locally compact abelian group in a straightforward way. For non-abelian groups
![]() $G$
, there is no Pontryagin dual; instead, the Fourier multiplier corresponding to a function
$G$
, there is no Pontryagin dual; instead, the Fourier multiplier corresponding to a function
![]() $\phi$
on
$\phi$
on
![]() $G$
is a map on the group von Neumann algebra. It is given by
$G$
is a map on the group von Neumann algebra. It is given by
![]() $\lambda _s \mapsto \phi (s) \lambda _s$
for
$\lambda _s \mapsto \phi (s) \lambda _s$
for
![]() $s \in G$
, where
$s \in G$
, where
![]() $\lambda$
is the left regular representation. Equivalently, it is given by
$\lambda$
is the left regular representation. Equivalently, it is given by
![]() $\lambda (f) \mapsto \lambda (\phi f)$
for
$\lambda (f) \mapsto \lambda (\phi f)$
for
![]() $f \in L_1(G)$
. It turns out that symbols
$f \in L_1(G)$
. It turns out that symbols
![]() $\phi \in L_\infty (G)$
give rise to bounded Fourier multipliers on
$\phi \in L_\infty (G)$
give rise to bounded Fourier multipliers on
![]() $\mathcal{L} G$
precisely when
$\mathcal{L} G$
precisely when
![]() $\phi$
defines a multiplier on the Fourier algebra
$\phi$
defines a multiplier on the Fourier algebra
![]() $A(G)$
, which coincides with the predual of
$A(G)$
, which coincides with the predual of
![]() $\mathcal{L} G$
.
$\mathcal{L} G$
.
Another interesting question is which symbols
![]() $\phi \in L_\infty (G)$
give rise to a completely bounded multiplier on
$\phi \in L_\infty (G)$
give rise to a completely bounded multiplier on
![]() $\mathcal{L} G$
. Bozejko and Fendler [Reference Bozejko and Fendler1] showed that this happens exactly when
$\mathcal{L} G$
. Bozejko and Fendler [Reference Bozejko and Fendler1] showed that this happens exactly when
![]() $\phi$
defines a bounded Schur multiplier of Toeplitz type on
$\phi$
defines a bounded Schur multiplier of Toeplitz type on
![]() $B(L_2(G))$
, and in that case, the completely bounded norms are equal. This is called a transference result between Fourier and Schur multipliers. A different proof of this transference result was later provided by Jolissaint [Reference Jolissaint13]. This relation between Fourier and Schur multipliers has been an important tool to prove several multiplier results. For instance, bounding the norm of Fourier multipliers by that of Schur multipliers played a crucial role in [Reference Parcet, Ricard and de la Salle21]. The converse transference was used in [Reference Pisier20] to give examples of bounded multipliers on
$B(L_2(G))$
, and in that case, the completely bounded norms are equal. This is called a transference result between Fourier and Schur multipliers. A different proof of this transference result was later provided by Jolissaint [Reference Jolissaint13]. This relation between Fourier and Schur multipliers has been an important tool to prove several multiplier results. For instance, bounding the norm of Fourier multipliers by that of Schur multipliers played a crucial role in [Reference Parcet, Ricard and de la Salle21]. The converse transference was used in [Reference Pisier20] to give examples of bounded multipliers on
![]() $L_p$
-spaces that are not completely bounded. Similar transference techniques were used in [Reference Conde-Alonso, González-Pérez, Parcet and Tablate4] to prove Hörmander-Mikhlin criteria for the boundedness of Schur multipliers and in [Reference Lafforgue and de la Salle17] to find examples of noncommutative
$L_p$
-spaces that are not completely bounded. Similar transference techniques were used in [Reference Conde-Alonso, González-Pérez, Parcet and Tablate4] to prove Hörmander-Mikhlin criteria for the boundedness of Schur multipliers and in [Reference Lafforgue and de la Salle17] to find examples of noncommutative
![]() $L_p$
-spaces without the completely bounded approximation property.
$L_p$
-spaces without the completely bounded approximation property.
There are several papers treating transference results for the noncommutative
![]() $L_p$
-spaces
$L_p$
-spaces
![]() $L_p(\mathcal{L} G)$
. Neuwirth and Ricard studied this question for discrete groups [Reference Neuwirth and Ricard18]. In this case, the Fourier multipliers are relatively straightforward to define on
$L_p(\mathcal{L} G)$
. Neuwirth and Ricard studied this question for discrete groups [Reference Neuwirth and Ricard18]. In this case, the Fourier multipliers are relatively straightforward to define on
![]() $L_p(\mathcal{L} G)$
. They proved that if
$L_p(\mathcal{L} G)$
. They proved that if
![]() $\phi$
defines a completely bounded Fourier multiplier on
$\phi$
defines a completely bounded Fourier multiplier on
![]() $L_p(\mathcal{L} G)$
, then it defines a completely bounded Schur multiplier on the Schatten class
$L_p(\mathcal{L} G)$
, then it defines a completely bounded Schur multiplier on the Schatten class
![]() $S_p(L_2(G))$
. Moreover, they proved that the converse implication also holds provided that the group
$S_p(L_2(G))$
. Moreover, they proved that the converse implication also holds provided that the group
![]() $G$
is amenable. Later, Caspers and De la Salle [Reference Caspers and de la Salle3] defined Fourier multipliers on the noncommutative
$G$
is amenable. Later, Caspers and De la Salle [Reference Caspers and de la Salle3] defined Fourier multipliers on the noncommutative
![]() $L_p$
-spaces of general locally compact groups and proved that the same transference results also hold here. An analogous result was proved by Gonzalez-Perez [Reference Gonzalez-Perez10] for crossed products.
$L_p$
-spaces of general locally compact groups and proved that the same transference results also hold here. An analogous result was proved by Gonzalez-Perez [Reference Gonzalez-Perez10] for crossed products.
Juschenko, Todorov and Turowska [Reference Juschenko, Todorov and Turowska14] introduced multilinear Schur multipliers with respect to measure spaces. Such multipliers and the related notion of multiple operator integrals have been used to prove several interesting results such as the resolution of Koplienko’s conjecture on higher order spectral shift functions in [Reference Potapov, Skripka and Sukochev22]. Therefore, it is also interesting to consider transference between multilinear Fourier and Schur multipliers. Todorov and Turowska [Reference Todorov26] defined a multidimensional Fourier algebra and proved a transference result for multiplicatively bounded multilinear Fourier and Schur multipliers.
To consider multilinear results on noncommutative
![]() $L_p$
-spaces, one needs a
$L_p$
-spaces, one needs a
![]() $(p_1, \dots, p_n)$
-version of multiplicative boundedness. This was introduced by Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5] along the lines of Pisier’s characterisation of completely bounded norms in terms of Schatten norms [Reference Pisier20, Lemma 1.7]. Moreover, they proved a bilinear transference result for discrete groups ‘along the way’ in [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Proof of Theorem 7.2], in order to provide examples of
$(p_1, \dots, p_n)$
-version of multiplicative boundedness. This was introduced by Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5] along the lines of Pisier’s characterisation of completely bounded norms in terms of Schatten norms [Reference Pisier20, Lemma 1.7]. Moreover, they proved a bilinear transference result for discrete groups ‘along the way’ in [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Proof of Theorem 7.2], in order to provide examples of
![]() $L_p$
-multipliers for semidirect products of groups. Multilinear transference was studied in a more general sense by Caspers, Krishnaswamy-Usha and the author of the present manuscript in [Reference Caspers, Krishnaswamy-Usha and Vos6], but only for unimodular groups. They obtained a generalisation of the linear transference results. As a direct consequence of this transference result, a De Leeuw-type restriction theorem was proven for the multiplicatively bounded norms. In this paper, we complete the picture by proving a multilinear transference result for general locally compact groups.
$L_p$
-multipliers for semidirect products of groups. Multilinear transference was studied in a more general sense by Caspers, Krishnaswamy-Usha and the author of the present manuscript in [Reference Caspers, Krishnaswamy-Usha and Vos6], but only for unimodular groups. They obtained a generalisation of the linear transference results. As a direct consequence of this transference result, a De Leeuw-type restriction theorem was proven for the multiplicatively bounded norms. In this paper, we complete the picture by proving a multilinear transference result for general locally compact groups.
The main difficulty for non-unimodular groups comes from the fact that the Plancherel weight is not tracial. This means that we have to deal with spatial derivatives, which in our case will just be the multiplication operator with the modular function. It will be denoted by
![]() $\Delta$
. In particular, this raises the question of how the multilinear Fourier multiplier should be defined for
$\Delta$
. In particular, this raises the question of how the multilinear Fourier multiplier should be defined for
![]() $p \lt \infty$
. It turns out that, in order to prove transference results, one needs to use the definition that ‘leaves the
$p \lt \infty$
. It turns out that, in order to prove transference results, one needs to use the definition that ‘leaves the
![]() $\Delta$
’s in place’. More precisely, for ‘suitable’
$\Delta$
’s in place’. More precisely, for ‘suitable’
![]() $f_i$
(this will be defined later) and
$f_i$
(this will be defined later) and
![]() $x_i = \Delta ^{\frac 1{2p_i}} \lambda (f_i) \Delta ^{\frac 1{2p_i}}$
, the Fourier multiplier is defined as
$x_i = \Delta ^{\frac 1{2p_i}} \lambda (f_i) \Delta ^{\frac 1{2p_i}}$
, the Fourier multiplier is defined as
A major drawback of this definition is that it is not suitable for interpolation results when
![]() $n \gt 2$
, unless the ‘intermediate’
$n \gt 2$
, unless the ‘intermediate’
![]() $p_i$
’s are all equal to
$p_i$
’s are all equal to
![]() $\infty$
, in which case it is open. All this will be discussed in Section 3. Our first main result gives the multilinear transference from Fourier multipliers as defined above to Schur multipliers. This is Theorem4.1. The definitions of
$\infty$
, in which case it is open. All this will be discussed in Section 3. Our first main result gives the multilinear transference from Fourier multipliers as defined above to Schur multipliers. This is Theorem4.1. The definitions of
![]() $(p_1, \dots, p_n)$
-multiplicative norms are given in Section 2.2.
$(p_1, \dots, p_n)$
-multiplicative norms are given in Section 2.2.
Theorem A.
Let
![]() $G$
be a locally compact first countable group, and let
$G$
be a locally compact first countable group, and let
![]() $1 \leq p \leq \infty$
,
$1 \leq p \leq \infty$
,
![]() $1\lt p_1, \ldots, p_n \leq \infty$
be such that
$1\lt p_1, \ldots, p_n \leq \infty$
be such that
![]() $p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
$p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
![]() $\phi \in C_b(G^{\times n})$
and define
$\phi \in C_b(G^{\times n})$
and define
![]() $\widetilde{\phi } \in C_b(G^{\times n + 1})$
by
$\widetilde{\phi } \in C_b(G^{\times n + 1})$
by
If
![]() $\phi$
is the symbol of a
$\phi$
is the symbol of a
![]() $(p_1, \ldots, p_n)$
-multiplicatively bounded Fourier multiplier
$(p_1, \ldots, p_n)$
-multiplicatively bounded Fourier multiplier
![]() $T_\phi$
of
$T_\phi$
of
![]() $G$
, then
$G$
, then
![]() $\widetilde{\phi }$
is the symbol of a
$\widetilde{\phi }$
is the symbol of a
![]() $(p_1, \ldots, p_n)$
-multiplicatively bounded Schur multiplier
$(p_1, \ldots, p_n)$
-multiplicatively bounded Schur multiplier
![]() $M_{\widetilde{\phi }}$
of
$M_{\widetilde{\phi }}$
of
![]() $G$
. Moreover,
$G$
. Moreover,
The proof is mostly an adaptation of the proof of [Reference Caspers, Krishnaswamy-Usha and Vos6, Theorem 3.1]. [Reference Caspers, Krishnaswamy-Usha and Vos6, Theorem 3.1] in turn has a large overlap with [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.6]. For that reason, the proof of [Reference Caspers, Krishnaswamy-Usha and Vos6, Theorem 3.1] only sketches the changes compared to [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.6]. As it seems undesirable to keep stacking sketches of changes, we have chosen to include the proof in full detail here. However, most of the work in generalising to the non-unimodular case comes from generalising the reduction lemmas [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemmas 4.3 and 4.4]. We do this already in Section 3. Note that [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.4] does not give any details for the proof even though it is not that trivial even in the unimodular case. In Lemma 3.8, we give an elegant induction argument that fills this gap.
Also, we need an extension of the intertwining result [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Proposition 3.9] for non-unimodular groups, which we state in Proposition 4.3. We will sketch the proof in a separate technical section at the end. We also note that in [Reference Caspers, Krishnaswamy-Usha and Vos6, Theorem 3.1], the group was required to be second countable, but in the proof, actually, only first countability was needed.
For amenable groups, we also have the converse transference result. In fact, one no longer needs a continuous symbol nor the first countability condition on the group. This is Corollary 5.2.
Theorem B.
Let
![]() $G$
be an amenable locally compact group and
$G$
be an amenable locally compact group and
![]() $1 \leq p, p_1, \dots, p_n \leq \infty$
be such that
$1 \leq p, p_1, \dots, p_n \leq \infty$
be such that
![]() $\frac 1p=\sum _{i=1}^n \frac 1{p_i}$
. Let
$\frac 1p=\sum _{i=1}^n \frac 1{p_i}$
. Let
![]() $\phi \in L_\infty (G^{\times n})$
and define
$\phi \in L_\infty (G^{\times n})$
and define
![]() $\widetilde{\phi }$
as in Theorem 1.1. If
$\widetilde{\phi }$
as in Theorem 1.1. If
![]() $\widetilde{\phi }$
is the symbol of a
$\widetilde{\phi }$
is the symbol of a
![]() $(p_1, \dots, p_n)$
-bounded (resp. multiplicatively bounded) Schur multiplier, then
$(p_1, \dots, p_n)$
-bounded (resp. multiplicatively bounded) Schur multiplier, then
![]() $\phi$
is the symbol of a
$\phi$
is the symbol of a
![]() $(p_1, \dots, p_n)$
-bounded (resp. multiplicatively bounded) Fourier multiplier. Moreover,
$(p_1, \dots, p_n)$
-bounded (resp. multiplicatively bounded) Fourier multiplier. Moreover,
Again, the proof is similar to [Reference Caspers, Krishnaswamy-Usha and Vos6] but with additional technical complications. We also abstain from using ultraproduct techniques since they were not actually necessary for the proof. It should be noted that if
![]() $p_i = \infty$
for some
$p_i = \infty$
for some
![]() $1 \leq i \leq n$
, then our methods only yield the above boundedness results of the multilinear Fourier multiplier on
$1 \leq i \leq n$
, then our methods only yield the above boundedness results of the multilinear Fourier multiplier on
![]() $C_\lambda ^*(G)$
in the
$C_\lambda ^*(G)$
in the
![]() $i$
’th input (and conversely, boundedness on
$i$
’th input (and conversely, boundedness on
![]() $C_\lambda ^*(G)$
is all we need for the converse direction in TheoremA). Of course, if
$C_\lambda ^*(G)$
is all we need for the converse direction in TheoremA). Of course, if
![]() $p_1 = \ldots = p_n = p = \infty$
, then the result from [Reference Todorov26] guarantees that the Fourier multiplier is indeed bounded on
$p_1 = \ldots = p_n = p = \infty$
, then the result from [Reference Todorov26] guarantees that the Fourier multiplier is indeed bounded on
![]() $(\mathcal{L} G)^{\times n}$
.
$(\mathcal{L} G)^{\times n}$
.
As a result of TheoremB, we again get a multilinear De Leeuw-type restriction theorem.
Finally, we describe the structure of the paper. We start by giving the necessary preliminaries in Section 2. We also give a new definition of (linear)
![]() $p$
-Fourier multipliers here. In Section 3, we discuss possible definitions of the multilinear Fourier multiplier and explain why the definition as stated above is the correct one for transference. We also prove some properties of the multilinear Fourier multiplier that we will need later. In Sections 4 and 5, we prove the transference from Fourier to Schur (TheoremA) and transference from Schur to Fourier (TheoremB), respectively. In Section 6, we sketch the proof of Proposition 4.3 using Haagerup reduction. This section is rather technical and not essential to understand the bigger picture.
$p$
-Fourier multipliers here. In Section 3, we discuss possible definitions of the multilinear Fourier multiplier and explain why the definition as stated above is the correct one for transference. We also prove some properties of the multilinear Fourier multiplier that we will need later. In Sections 4 and 5, we prove the transference from Fourier to Schur (TheoremA) and transference from Schur to Fourier (TheoremB), respectively. In Section 6, we sketch the proof of Proposition 4.3 using Haagerup reduction. This section is rather technical and not essential to understand the bigger picture.
2. Preliminaries
A more elaborate discussion of some of the statements in this section is contained in the author’s PhD thesis [Reference Vos27].
2.1. L p -spaces of group von Neumann algebras for noncommutative groups
Let
![]() $G$
be a locally compact group, not necessarily unimodular. We will denote the left Haar measure of such a group by
$G$
be a locally compact group, not necessarily unimodular. We will denote the left Haar measure of such a group by
![]() $\mu \,:\!=\, \mu _G$
. Its modular function will be denoted by
$\mu \,:\!=\, \mu _G$
. Its modular function will be denoted by
![]() $\Delta$
. Recall that
$\Delta$
. Recall that
![]() $\Delta \,:\, G \to ({\mathrm{\mathbb{R}}}_{\gt 0}, \times )$
is a continuous group homomorphism satisfying
$\Delta \,:\, G \to ({\mathrm{\mathbb{R}}}_{\gt 0}, \times )$
is a continuous group homomorphism satisfying
In the sequel, we will write
![]() $ds$
for the left Haar measure.
$ds$
for the left Haar measure.
The left regular representation
![]() $\lambda$
acts on
$\lambda$
acts on
![]() $L_2(G)$
by
$L_2(G)$
by
![]() $(\lambda _sf)(t) = f(s^{-1}t)$
. It also defines a
$(\lambda _sf)(t) = f(s^{-1}t)$
. It also defines a
![]() $*$
-representation of the
$*$
-representation of the
![]() $*$
-algebra
$*$
-algebra
![]() $L_1(G)$
on
$L_1(G)$
on
![]() $L_2(G)$
by the formula
$L_2(G)$
by the formula
The group von Neumann algebra
![]() $\mathcal{L} G$
of
$\mathcal{L} G$
of
![]() $G$
is defined as
$G$
is defined as
The group von Neumann algebra admits a canonical weight
![]() $\varphi$
, named the Plancherel weight. It is defined for
$\varphi$
, named the Plancherel weight. It is defined for
![]() $x \in \mathcal{L} G$
by
$x \in \mathcal{L} G$
by
 \begin{equation*} \varphi (x^*x) = \begin {cases} \|f\|_2^2 \qquad & \text {if } x = \lambda (f) \text { for some } f \in L_2(G) \\ \infty & \text {else}. \end {cases} \end{equation*}
\begin{equation*} \varphi (x^*x) = \begin {cases} \|f\|_2^2 \qquad & \text {if } x = \lambda (f) \text { for some } f \in L_2(G) \\ \infty & \text {else}. \end {cases} \end{equation*}
Here, we extend
![]() $\lambda$
to all functions that define a bounded convolution operator. The Plancherel weight is tracial if and only if
$\lambda$
to all functions that define a bounded convolution operator. The Plancherel weight is tracial if and only if
![]() $G$
is unimodular. Similarly, there is a right regular representation
$G$
is unimodular. Similarly, there is a right regular representation
![]() $\rho$
defined by
$\rho$
defined by
![]() $(\rho _sf)(t) = \Delta ^{1/2}(s) f(ts)$
and a Plancherel weight
$(\rho _sf)(t) = \Delta ^{1/2}(s) f(ts)$
and a Plancherel weight
![]() $\psi$
on
$\psi$
on
![]() $(\mathcal{L} G)^{\prime}$
defined as
$(\mathcal{L} G)^{\prime}$
defined as
![]() $\psi (x^*x) = \|f\|^2_2$
if
$\psi (x^*x) = \|f\|^2_2$
if
![]() $x$
is given by
$x$
is given by
![]() $x = \rho (f)$
for some
$x = \rho (f)$
for some
![]() $f \in L_2(G)$
and
$f \in L_2(G)$
and
![]() $\psi (x) = \infty$
otherwise. In practice, the group
$\psi (x) = \infty$
otherwise. In practice, the group
![]() $\mathcal{L} G$
is often semifinite even when
$\mathcal{L} G$
is often semifinite even when
![]() $G$
is not unimodular, but it is more natural to work with the Plancherel weight. For instance, the definition of
$G$
is not unimodular, but it is more natural to work with the Plancherel weight. For instance, the definition of
![]() $\varphi$
gives the Plancherel identity (2.2) below.
$\varphi$
gives the Plancherel identity (2.2) below.
Let
![]() $L_p(\mathcal{L} G)$
denote the Connes–Hilsum
$L_p(\mathcal{L} G)$
denote the Connes–Hilsum
![]() $L_p$
-space corresponding to the Plancherel weight
$L_p$
-space corresponding to the Plancherel weight
![]() $\psi$
on
$\psi$
on
![]() $(\mathcal{L} G)^{\prime}$
([Reference Connes7],[Reference Hilsum11]; see also [Reference Terp25]). To keep this paper more accessible, we will not be using the Tomita–Takesaki theory or the theory of spatial derivatives, except for the last section. Instead, we will use some facts about the Connes–Hilsum
$(\mathcal{L} G)^{\prime}$
([Reference Connes7],[Reference Hilsum11]; see also [Reference Terp25]). To keep this paper more accessible, we will not be using the Tomita–Takesaki theory or the theory of spatial derivatives, except for the last section. Instead, we will use some facts about the Connes–Hilsum
![]() $L_p$
-spaces as a black box. First, for
$L_p$
-spaces as a black box. First, for
![]() $1 \leq p \lt \infty$
, elements of
$1 \leq p \lt \infty$
, elements of
![]() $L_p(\mathcal{L} G)$
are closed unbounded operators on
$L_p(\mathcal{L} G)$
are closed unbounded operators on
![]() $L_2(G)$
, and sums and products of such operators are densely defined and preclosed. Addition and multiplication on
$L_2(G)$
, and sums and products of such operators are densely defined and preclosed. Addition and multiplication on
![]() $L_p(\mathcal{L} G)$
are defined by taking the closures of the resulting sum resp. product, and we will use the usual addition and multiplication notations for this. For any
$L_p(\mathcal{L} G)$
are defined by taking the closures of the resulting sum resp. product, and we will use the usual addition and multiplication notations for this. For any
![]() $x \in L_p(\mathcal{L} G)$
,
$x \in L_p(\mathcal{L} G)$
,
![]() $1 \leq p \leq \infty$
, we have
$1 \leq p \leq \infty$
, we have
The spatial derivative
![]() $\frac{d\varphi }{d\psi }$
is just multiplication with the modular function
$\frac{d\varphi }{d\psi }$
is just multiplication with the modular function
![]() $\Delta$
; see, for instance, [Reference Caspers and de la Salle3, Section 3.5] for more details. With slight abuse of notation, we will denote this operator by
$\Delta$
; see, for instance, [Reference Caspers and de la Salle3, Section 3.5] for more details. With slight abuse of notation, we will denote this operator by
![]() $\Delta$
as well. The domain of this operator is exactly the set of functions
$\Delta$
as well. The domain of this operator is exactly the set of functions
![]() $f \in L_2(G)$
such that
$f \in L_2(G)$
such that
![]() $\int _G \Delta ^2(s) |f(s)|^2 ds \lt \infty$
. Usually, we will only apply
$\int _G \Delta ^2(s) |f(s)|^2 ds \lt \infty$
. Usually, we will only apply
![]() $\Delta$
to continuous compactly supported functions so that no technical complications can arise.
$\Delta$
to continuous compactly supported functions so that no technical complications can arise.
Now define
![]() $L \,:\!=\, \lambda (C_c(G) \star C_c(G))$
, where
$L \,:\!=\, \lambda (C_c(G) \star C_c(G))$
, where
![]() $C_c(G) \star C_c(G)$
is the linear span of elements of the form
$C_c(G) \star C_c(G)$
is the linear span of elements of the form
![]() $f * g$
,
$f * g$
,
![]() $f, g \in C_c(G)$
. For
$f, g \in C_c(G)$
. For
![]() $\theta \in [0,1]$
and
$\theta \in [0,1]$
and
![]() $1 \leq p \lt \infty$
, there is an embedding
$1 \leq p \lt \infty$
, there is an embedding
![]() $\kappa ^{\theta }_p\,:\, L \to L_p(\mathcal{L} G)$
given by
$\kappa ^{\theta }_p\,:\, L \to L_p(\mathcal{L} G)$
given by
For
![]() $p = \infty$
, we simply set
$p = \infty$
, we simply set
![]() ${\kappa }_p^\theta$
to be the identity. The images of the embeddings
${\kappa }_p^\theta$
to be the identity. The images of the embeddings
![]() ${\kappa }^{\theta }_p$
are dense in
${\kappa }^{\theta }_p$
are dense in
![]() $L_p(\mathcal{L} G)$
, which will be crucial in the rest of the paper.
$L_p(\mathcal{L} G)$
, which will be crucial in the rest of the paper.
We now state some other facts for later use. From the definitions of the
![]() $L_p$
-norm and the Plancherel weight, we have the following Plancherel identity:
$L_p$
-norm and the Plancherel weight, we have the following Plancherel identity:
As a side note, this implies that the map
![]() $C_c(G) \mapsto{\kappa }_2^1(\lambda (C_c(G)))$
,
$C_c(G) \mapsto{\kappa }_2^1(\lambda (C_c(G)))$
,
![]() $f \mapsto \lambda (f) \Delta ^{1/2}$
extends to a unitary
$f \mapsto \lambda (f) \Delta ^{1/2}$
extends to a unitary
![]() $L_2(G) \cong L_2(\mathcal{L} G)$
. Next, a straightforward calculation yields the following commutation formulae:
$L_2(G) \cong L_2(\mathcal{L} G)$
. Next, a straightforward calculation yields the following commutation formulae:
and
Also, note that for
![]() $f = g * h$
,
$f = g * h$
,
![]() $g,h \in C_c(G)$
and
$g,h \in C_c(G)$
and
![]() $z \in{\mathrm{\mathbb{C}}}$
, we have
$z \in{\mathrm{\mathbb{C}}}$
, we have
and therefore
![]() $\Delta ^z (C_c(G) \star C_c(G)) = C_c(G) \star C_c(G)$
. Hence, (2.4) yields that
$\Delta ^z (C_c(G) \star C_c(G)) = C_c(G) \star C_c(G)$
. Hence, (2.4) yields that
2.2. Operator spaces and multiplicatively bounded maps
Let
![]() $E_1, \dots, E_n, E$
be operator spaces and
$E_1, \dots, E_n, E$
be operator spaces and
![]() $T\,:\, E_1 \times \ldots \times E_n \to E$
a linear map. For
$T\,:\, E_1 \times \ldots \times E_n \to E$
a linear map. For
![]() $N \geq 1$
, the multiplicative amplification
$N \geq 1$
, the multiplicative amplification
![]() $T^{(N)}\,:\, M_N(E_1) \times \ldots M_N(E_n) \to M_N(E)$
of
$T^{(N)}\,:\, M_N(E_1) \times \ldots M_N(E_n) \to M_N(E)$
of
![]() $T$
is defined as
$T$
is defined as
and extended linearly. The map
![]() $T$
is said to be multiplicatively bounded if
$T$
is said to be multiplicatively bounded if
Let us now define a notion of
![]() $p$
-completely bounded maps. Set
$p$
-completely bounded maps. Set
![]() $E = L_p(\mathcal{M}, \psi )$
for some von Neumann algebra
$E = L_p(\mathcal{M}, \psi )$
for some von Neumann algebra
![]() $\mathcal{M}$
and normal faithful semifinite weight
$\mathcal{M}$
and normal faithful semifinite weight
![]() $\psi$
on
$\psi$
on
![]() $\mathcal{M}^{\prime}$
. Let
$\mathcal{M}^{\prime}$
. Let
![]() $x \in M_N(E)$
; then
$x \in M_N(E)$
; then
![]() $x$
is closable and
$x$
is closable and
![]() $[x] \in L_p(M_n(\mathcal{M}), \mathrm{tr}_N \otimes \psi )$
. Here
$[x] \in L_p(M_n(\mathcal{M}), \mathrm{tr}_N \otimes \psi )$
. Here
![]() $\mathrm{tr}_N$
is the trace on
$\mathrm{tr}_N$
is the trace on
![]() $M_N({\mathrm{\mathbb{C}}})$
. Now we set
$M_N({\mathrm{\mathbb{C}}})$
. Now we set
![]() $S_p^N \otimes L_p(\mathcal{M}, \psi )$
to be the space
$S_p^N \otimes L_p(\mathcal{M}, \psi )$
to be the space
![]() $M_n(L_p(\mathcal{M}, \psi ))$
equipped with the norm
$M_n(L_p(\mathcal{M}, \psi ))$
equipped with the norm
We say that an operator
![]() $T\,:\, L_p(\mathcal{M}, \psi ) \to L_p(\mathcal{M}, \psi )$
is
$T\,:\, L_p(\mathcal{M}, \psi ) \to L_p(\mathcal{M}, \psi )$
is
![]() $p$
-completely bounded if
$p$
-completely bounded if
The matrix norms satisfy
For semifinite
![]() $\mathcal{M}$
, this is an easy exercise; for arbitrary von Neumann algebras, this requires some analysis on the interplay between spatial derivatives and matrices.
$\mathcal{M}$
, this is an easy exercise; for arbitrary von Neumann algebras, this requires some analysis on the interplay between spatial derivatives and matrices.
We note that the norm on
![]() $S_p^N \otimes L_p(\mathcal{M}, \psi )$
does not give an operator space structure on
$S_p^N \otimes L_p(\mathcal{M}, \psi )$
does not give an operator space structure on
![]() $L_p(\mathcal{M}, \psi )$
, as it does not satisfy the axioms. However, if
$L_p(\mathcal{M}, \psi )$
, as it does not satisfy the axioms. However, if
![]() $\mathcal{M}$
is semifinite, then the notion of
$\mathcal{M}$
is semifinite, then the notion of
![]() $p$
-completely bounded maps coincides with the usual notion of completely bounded maps by [Reference Pisier20].
$p$
-completely bounded maps coincides with the usual notion of completely bounded maps by [Reference Pisier20].
We now define a
![]() $(p_1, \dots, p_n)$
-multiplicatively bounded norm in a similar manner. Let
$(p_1, \dots, p_n)$
-multiplicatively bounded norm in a similar manner. Let
![]() $1 \leq p_1, \dots, p_n, p \leq \infty$
with
$1 \leq p_1, \dots, p_n, p \leq \infty$
with
![]() $p^{-1} = \sum _{i=1}^n p_i^{-1}$
. We define a map
$p^{-1} = \sum _{i=1}^n p_i^{-1}$
. We define a map
![]() $T\,:\, L_{p_1}(\mathcal{M}) \times \ldots \times L_{p_n}(\mathcal{M}) \to L_p(\mathcal{M})$
to be
$T\,:\, L_{p_1}(\mathcal{M}) \times \ldots \times L_{p_n}(\mathcal{M}) \to L_p(\mathcal{M})$
to be
![]() $(p_1, \dots, p_n)$
-multiplicatively bounded if
$(p_1, \dots, p_n)$
-multiplicatively bounded if
This turns out to be the correct notion to prove our transference results. We note that this time, there does not seem to be a case for which this coincides with ‘normal’ multiplicative boundedness, as [Reference Pisier20, Lemma 1.7] does not generalise to the multilinear case. If
![]() $\mathcal{M}$
is semifinite, then the above definition does coincide with the definition of
$\mathcal{M}$
is semifinite, then the above definition does coincide with the definition of
![]() $(p_1, \dots, p_n)$
-multiplicative boundedness from [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5] and [Reference Caspers, Krishnaswamy-Usha and Vos6]. Even in the semifinite case, it is unclear if this definition corresponds to the complete boundedness of some linear map on some appropriate tensor product; see [Reference Caspers, Krishnaswamy-Usha and Vos6, Remark 2.1].
$(p_1, \dots, p_n)$
-multiplicative boundedness from [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5] and [Reference Caspers, Krishnaswamy-Usha and Vos6]. Even in the semifinite case, it is unclear if this definition corresponds to the complete boundedness of some linear map on some appropriate tensor product; see [Reference Caspers, Krishnaswamy-Usha and Vos6, Remark 2.1].
2.3. Fourier multipliers
Again let
![]() $G$
be a locally compact group. For a bounded function
$G$
be a locally compact group. For a bounded function
![]() $\phi \,:\, G \to{\mathrm{\mathbb{C}}}$
, the associated Fourier multiplier
$\phi \,:\, G \to{\mathrm{\mathbb{C}}}$
, the associated Fourier multiplier
![]() $T_\phi \,:\, \mathcal{L} G \to \mathcal{L} G$
is given for
$T_\phi \,:\, \mathcal{L} G \to \mathcal{L} G$
is given for
![]() $f \in L_1(G)$
by
$f \in L_1(G)$
by
![]() $\lambda (f) \mapsto \lambda (\phi f)$
, whenever this map extends weak-* continuously. This definition has been extended to
$\lambda (f) \mapsto \lambda (\phi f)$
, whenever this map extends weak-* continuously. This definition has been extended to
![]() $L_p(\mathcal{L} G)$
for general locally compact groups in [Reference Caspers and de la Salle3]. However, this was done only for symbols
$L_p(\mathcal{L} G)$
for general locally compact groups in [Reference Caspers and de la Salle3]. However, this was done only for symbols
![]() $\phi \in M_{cb}A(G)$
, that is, those symbols for which
$\phi \in M_{cb}A(G)$
, that is, those symbols for which
![]() $T_\phi$
defines a completely bounded multiplier on
$T_\phi$
defines a completely bounded multiplier on
![]() $\mathcal{L} G$
. We give a broader definition here as preparation for the multilinear definition. Define
$\mathcal{L} G$
. We give a broader definition here as preparation for the multilinear definition. Define
![]() $\overline{\mathcal{L} G}_{(\gamma )}$
to be the space of closed densely defined
$\overline{\mathcal{L} G}_{(\gamma )}$
to be the space of closed densely defined
![]() $\gamma$
-homogeneous operators on
$\gamma$
-homogeneous operators on
![]() $L_2(G)$
. See [Reference Terp25, Section III, IV] for a definition and some properties. We use here the facts that this space contains
$L_2(G)$
. See [Reference Terp25, Section III, IV] for a definition and some properties. We use here the facts that this space contains
![]() $L_p(\mathcal{L} G)$
and that the right-hand side of (2.8) is always in
$L_p(\mathcal{L} G)$
and that the right-hand side of (2.8) is always in
![]() $\overline{\mathcal{L} G}_{(-1/p)}$
([Reference Terp25, III.(19) and Corollary III.34]).
$\overline{\mathcal{L} G}_{(-1/p)}$
([Reference Terp25, III.(19) and Corollary III.34]).
For
![]() $\phi \in L_\infty (G)$
, define
$\phi \in L_\infty (G)$
, define
![]() $T_\phi \,:\,{\kappa }_p^\theta (L) \to \overline{\mathcal{L} G}_{(-1/p)}$
by
$T_\phi \,:\,{\kappa }_p^\theta (L) \to \overline{\mathcal{L} G}_{(-1/p)}$
by
The map
![]() $T_\phi$
does not depend on the choice of
$T_\phi$
does not depend on the choice of
![]() $\theta$
; this follows from (2.6) and some manipulations using the commutation formula (2.4). When the image of
$\theta$
; this follows from (2.6) and some manipulations using the commutation formula (2.4). When the image of
![]() $T_\phi$
lies in
$T_\phi$
lies in
![]() $L_p(\mathcal{L} G)$
and
$L_p(\mathcal{L} G)$
and
![]() $T_\phi$
extends continuously to a bounded map on
$T_\phi$
extends continuously to a bounded map on
![]() $L_p(\mathcal{L} G)$
, we say that
$L_p(\mathcal{L} G)$
, we say that
![]() $\phi$
defines a
$\phi$
defines a
![]() $p$
-Fourier multiplier. When the extension is moreover
$p$
-Fourier multiplier. When the extension is moreover
![]() $p$
-completely bounded on
$p$
-completely bounded on
![]() $L_p(\mathcal{L} G)$
, we say
$L_p(\mathcal{L} G)$
, we say
![]() $\phi$
defines a
$\phi$
defines a
![]() $p$
-cb Fourier multiplier. For
$p$
-cb Fourier multiplier. For
![]() $\phi \in M_{cb}A(G)$
, the definition of the Fourier multiplier coincides with that of [Reference Caspers and de la Salle3]. For
$\phi \in M_{cb}A(G)$
, the definition of the Fourier multiplier coincides with that of [Reference Caspers and de la Salle3]. For
![]() $p=1$
, this can be shown by using [Reference Caspers and de la Salle3, Proposition-Definition 3.5] and (2.10) below together with [Reference Caspers and de la Salle3, Theorem 6.2 (ii), (iv)]; for other
$p=1$
, this can be shown by using [Reference Caspers and de la Salle3, Proposition-Definition 3.5] and (2.10) below together with [Reference Caspers and de la Salle3, Theorem 6.2 (ii), (iv)]; for other
![]() $p$
, this follows by interpolation.
$p$
, this follows by interpolation.
Let us now state some known results about when symbols define
![]() $p$
- or
$p$
- or
![]() $p$
-cb Fourier multipliers. Let
$p$
-cb Fourier multipliers. Let
![]() $A(G)$
be the Fourier algebra; it is defined as
$A(G)$
be the Fourier algebra; it is defined as
![]() $A(G) = \{f * \tilde{g}\,:\, f, g \in L_2(G)\}$
where
$A(G) = \{f * \tilde{g}\,:\, f, g \in L_2(G)\}$
where
![]() $\tilde{g}(s) = \overline{g(s^{-1})}$
. It is isomorphic to
$\tilde{g}(s) = \overline{g(s^{-1})}$
. It is isomorphic to
![]() $L_1(\mathcal{L} G)$
, the predual of
$L_1(\mathcal{L} G)$
, the predual of
![]() $\mathcal{L} G$
, through the pairing
$\mathcal{L} G$
, through the pairing
From classical theory (see, e.g. [Reference Kaniuth and Lau16, Proposition 5.1.2]), it is known that
![]() $\phi \in M(A(G))$
if and only if
$\phi \in M(A(G))$
if and only if
![]() $\phi$
defines a
$\phi$
defines a
![]() $\infty$
-Fourier multiplier. In the same way as in [Reference Caspers and de la Salle3, Proof of Definition-Proposition 3.5], one proves that in this case,
$\infty$
-Fourier multiplier. In the same way as in [Reference Caspers and de la Salle3, Proof of Definition-Proposition 3.5], one proves that in this case,
![]() $\phi$
defines a
$\phi$
defines a
![]() $p$
-Fourier multiplier for all
$p$
-Fourier multiplier for all
![]() $1 \leq p \leq \infty$
. Trivially,
$1 \leq p \leq \infty$
. Trivially,
![]() $A(G) \subseteq M(A(G))$
, and hence
$A(G) \subseteq M(A(G))$
, and hence
![]() $A(G)$
provides us with plenty of symbols defining
$A(G)$
provides us with plenty of symbols defining
![]() $p$
-Fourier multipliers; we will use this fact later on. As mentioned above, if
$p$
-Fourier multipliers; we will use this fact later on. As mentioned above, if
![]() $\phi$
is a
$\phi$
is a
![]() $\infty$
-cb Fourier multiplier (i.e.
$\infty$
-cb Fourier multiplier (i.e.
![]() $\phi \in M_{cb}A(G)$
), then
$\phi \in M_{cb}A(G)$
), then
![]() $\phi$
is also a
$\phi$
is also a
![]() $p$
-cb Fourier multiplier for
$p$
-cb Fourier multiplier for
![]() $1 \leq p \leq \infty$
. This is proven in [Reference Caspers and de la Salle3, Definition-Proposition 3.5].
$1 \leq p \leq \infty$
. This is proven in [Reference Caspers and de la Salle3, Definition-Proposition 3.5].
Let us now turn our attention to the multilinear case. In [Reference Todorov26],
![]() $M^{cb}_nA(G)$
was defined to be the space of all symbols
$M^{cb}_nA(G)$
was defined to be the space of all symbols
![]() $\phi \in L_\infty (G^{\times n})$
such that the map
$\phi \in L_\infty (G^{\times n})$
such that the map
extends to a multiplicatively bounded normal map
![]() $(\mathcal{L} G)^{\times n} \to \mathcal{L} G$
. In [Reference Caspers, Krishnaswamy-Usha and Vos6], multilinear Fourier multipliers on the noncommutative
$(\mathcal{L} G)^{\times n} \to \mathcal{L} G$
. In [Reference Caspers, Krishnaswamy-Usha and Vos6], multilinear Fourier multipliers on the noncommutative
![]() $L_p$
-spaces were defined for unimodular groups
$L_p$
-spaces were defined for unimodular groups
![]() $G$
as follows. Let
$G$
as follows. Let
![]() $\phi \in L_\infty (G^{\times n})$
and
$\phi \in L_\infty (G^{\times n})$
and
![]() $1\leq p_1, \ldots, p_n, p \lt \infty$
with
$1\leq p_1, \ldots, p_n, p \lt \infty$
with
![]() $p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Consider the map
$p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Consider the map
![]() $T_\phi \,:\, L^{\times n} \to \mathcal{L} G$
defined by
$T_\phi \,:\, L^{\times n} \to \mathcal{L} G$
defined by
for
![]() $f_i \in C_c(G) \star C_c(G)$
. If this map takes values in
$f_i \in C_c(G) \star C_c(G)$
. If this map takes values in
![]() $L_p(\mathcal{L} G)$
and extends continuously to
$L_p(\mathcal{L} G)$
and extends continuously to
![]() $L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_n}(\mathcal{L} G)$
, then we say that
$L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_n}(\mathcal{L} G)$
, then we say that
![]() $\phi$
defines a
$\phi$
defines a
![]() $(p_1, \dots, p_n)$
-Fourier multiplier. The extension is again denoted by
$(p_1, \dots, p_n)$
-Fourier multiplier. The extension is again denoted by
![]() $T_\phi$
. In case
$T_\phi$
. In case
![]() $p_i = \infty$
, we replace
$p_i = \infty$
, we replace
![]() $L_{p_i}(\mathcal{L} G)$
by
$L_{p_i}(\mathcal{L} G)$
by
![]() $C_\lambda ^*(G)$
in the
$C_\lambda ^*(G)$
in the
![]() $i$
’th coordinate. If the extension is
$i$
’th coordinate. If the extension is
![]() $(p_1, \dots, p_n$
)-multiplicatively bounded, then we say that
$(p_1, \dots, p_n$
)-multiplicatively bounded, then we say that
![]() $\phi$
defines a
$\phi$
defines a
![]() $(p_1, \dots, p_n)$
-mb Fourier multiplier.
$(p_1, \dots, p_n)$
-mb Fourier multiplier.
This definition works only for unimodular groups if
![]() $p \lt \infty$
since
$p \lt \infty$
since
![]() $L$
is not contained in
$L$
is not contained in
![]() $L_p(\mathcal{L} G)$
otherwise. In Section 3, we will give the definition for non-unimodular groups.
$L_p(\mathcal{L} G)$
otherwise. In Section 3, we will give the definition for non-unimodular groups.
Remark 2.1.
We note that a priori, the set of symbols of
![]() $(\infty, \dots, \infty )$
-mb Fourier multipliers is smaller than
$(\infty, \dots, \infty )$
-mb Fourier multipliers is smaller than
![]() $M_n^{cb}A(G)$
. However, these sets are actually the same. This follows, for instance, from a combination of our results and [Reference Todorov26
, Theorem 5.5]. One does not need the complicated machinery of Section
4
however. It follows already from the proof of [
Reference Todorov26, Theorem 5.5] or from the alternative proof of the Fourier to Schur direction in [Reference Caspers, Krishnaswamy-Usha and Vos6
, Proposition 2.3], which it suffices to require that
$M_n^{cb}A(G)$
. However, these sets are actually the same. This follows, for instance, from a combination of our results and [Reference Todorov26
, Theorem 5.5]. One does not need the complicated machinery of Section
4
however. It follows already from the proof of [
Reference Todorov26, Theorem 5.5] or from the alternative proof of the Fourier to Schur direction in [Reference Caspers, Krishnaswamy-Usha and Vos6
, Proposition 2.3], which it suffices to require that
![]() $T_\phi$
is bounded on
$T_\phi$
is bounded on
![]() $(C_\lambda ^*(G))^{\times n}$
.
$(C_\lambda ^*(G))^{\times n}$
.
2.4. Schatten classes and Schur multipliers
We denote by
![]() $S_p(H)$
the standard Schatten classes on the Hilbert space
$S_p(H)$
the standard Schatten classes on the Hilbert space
![]() $H$
. If
$H$
. If
![]() $(X, \mu )$
is some measure space, then
$(X, \mu )$
is some measure space, then
![]() $S_2(L_2(X))$
can be isometrically identified with the space of kernels
$S_2(L_2(X))$
can be isometrically identified with the space of kernels
![]() $L_2(X \times X)$
. Through this identification, a kernel
$L_2(X \times X)$
. Through this identification, a kernel
![]() $A \in L_2(X \times X)$
corresponds to the operator
$A \in L_2(X \times X)$
corresponds to the operator
![]() $(A\xi )(s) = \int _X A(s,t) \xi (t) dt$
. This should be seen as a continuous version of matrix multiplication. We will make no distinction between an operator
$(A\xi )(s) = \int _X A(s,t) \xi (t) dt$
. This should be seen as a continuous version of matrix multiplication. We will make no distinction between an operator
![]() $A$
and its kernel. For
$A$
and its kernel. For
![]() $1 \leq p \leq 2 \leq p^{\prime} \leq \infty$
with
$1 \leq p \leq 2 \leq p^{\prime} \leq \infty$
with
![]() $\frac 1p + \frac 1{p^{\prime}} = 1$
, the dual pairing between
$\frac 1p + \frac 1{p^{\prime}} = 1$
, the dual pairing between
![]() $S_p(L_2(X))$
and
$S_p(L_2(X))$
and
![]() $S_{p^{\prime}}(L_2(X))$
is given by
$S_{p^{\prime}}(L_2(X))$
is given by
This assignment is extended continuously for general
![]() $B \in S_{p^{\prime}}(L_2(X))$
. We refer to [Reference Lafforgue and de la Salle17] Section 1.2] for more details.
$B \in S_{p^{\prime}}(L_2(X))$
. We refer to [Reference Lafforgue and de la Salle17] Section 1.2] for more details.
For
![]() $\phi \in L_\infty (X^{\times n+1})$
, the associated Schur multiplier is the multilinear map
$\phi \in L_\infty (X^{\times n+1})$
, the associated Schur multiplier is the multilinear map
![]() $S_2(L_2(X))\times \ldots \times S_2(L_2(X)) \to S_2(L_2(X))$
determined by
$S_2(L_2(X))\times \ldots \times S_2(L_2(X)) \to S_2(L_2(X))$
determined by
It follows by Cauchy–Schwarz and a straightforward calculation that
![]() $M_\phi$
does indeed take values in
$M_\phi$
does indeed take values in
![]() $S_2(L_2(X))$
(see, for instance, [Reference Caspers, Krishnaswamy-Usha and Vos6]). Now let
$S_2(L_2(X))$
(see, for instance, [Reference Caspers, Krishnaswamy-Usha and Vos6]). Now let
![]() $1\leq p,p_1,\ldots, p_n \leq \infty$
, with
$1\leq p,p_1,\ldots, p_n \leq \infty$
, with
![]() $p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Restrict
$p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Restrict
![]() $M_\phi$
in the
$M_\phi$
in the
![]() $i$
-th input to
$i$
-th input to
![]() $S_2(L_2(X)) \cap S_{p_i}(L_2(X))$
. Assume that this restriction maps to
$S_2(L_2(X)) \cap S_{p_i}(L_2(X))$
. Assume that this restriction maps to
![]() $S_p(L_2(X))$
and has a bounded extension to
$S_p(L_2(X))$
and has a bounded extension to
![]() $S_{p_1}(L_2(X)) \times \ldots \times S_{p_n}(L_2(X))$
. Then we say that
$S_{p_1}(L_2(X)) \times \ldots \times S_{p_n}(L_2(X))$
. Then we say that
![]() $\phi$
defines a
$\phi$
defines a
![]() $(p_1, \dots, p_n)$
-Schur multiplier. Its extension is again denoted by
$(p_1, \dots, p_n)$
-Schur multiplier. Its extension is again denoted by
![]() $M_\phi$
. If
$M_\phi$
. If
![]() $M_\phi$
is
$M_\phi$
is
![]() $(p_1, \dots, p_n)$
-multiplicatively bounded, then we say that
$(p_1, \dots, p_n)$
-multiplicatively bounded, then we say that
![]() $\phi$
defines a
$\phi$
defines a
![]() $(p_1, \dots, p_n)$
-mb Schur multiplier.
$(p_1, \dots, p_n)$
-mb Schur multiplier.
The following theorem is [Reference Caspers, Krishnaswamy-Usha and Vos6, Theorem 2.2]; see also [Reference Lafforgue and de la Salle17, Theorem 1.19] and [Reference Caspers and de la Salle3, Theorem 3.1]. It will be the starting point for the proof of Theorem4.1.
Theorem 2.2.
Let
![]() $\mu$
be a Radon measure on a locally compact space
$\mu$
be a Radon measure on a locally compact space
![]() $X$
and
$X$
and
![]() $\phi \,:\, X^{n+1} \to{\mathrm{\mathbb{C}}}$
a continuous function. Let
$\phi \,:\, X^{n+1} \to{\mathrm{\mathbb{C}}}$
a continuous function. Let
![]() $K\gt 0$
. The following are equivalent for
$K\gt 0$
. The following are equivalent for
![]() $1 \leq p_1, \dots, p_n, p \leq \infty$
:
$1 \leq p_1, \dots, p_n, p \leq \infty$
:
-
(i)
 $\phi$
defines a bounded Schur multiplier
$\phi$
defines a bounded Schur multiplier
 $S_{p_1}(L_2(X)) \times \ldots \times S_{p_n}(L_2(X)) \to S_p(L_2(X))$
with norm less than
$S_{p_1}(L_2(X)) \times \ldots \times S_{p_n}(L_2(X)) \to S_p(L_2(X))$
with norm less than
 $K$
.
$K$
. -
(ii) For every
 $\sigma$
-finite measurable subset
$\sigma$
-finite measurable subset
 $X_0$
in
$X_0$
in
 $X$
,
$X$
,
 $\phi$
restricts to a bounded Schur multiplier
$\phi$
restricts to a bounded Schur multiplier
 $S_{p_1}(L_2(X_0)) \times \ldots \times S_{p_n}(L_2(X_0)) \to S_p(L_2(X_0))$
with norm less than
$S_{p_1}(L_2(X_0)) \times \ldots \times S_{p_n}(L_2(X_0)) \to S_p(L_2(X_0))$
with norm less than
 $K$
.
$K$
. -
(iii) For any finite subset
 $F = \{s_1, \dots, s_N\} \subset X$
belonging to the support of
$F = \{s_1, \dots, s_N\} \subset X$
belonging to the support of
 $\mu$
, the symbol
$\mu$
, the symbol
 $\phi |_{F^{\times (n+1)}}$
defines a bounded Schur multiplier
$\phi |_{F^{\times (n+1)}}$
defines a bounded Schur multiplier
 $S_{p_1}(\ell _2(F)) \times \ldots \times S_{p_2}(\ell _2(F)) \to S_p(\ell _2(F))$
with norm less than
$S_{p_1}(\ell _2(F)) \times \ldots \times S_{p_2}(\ell _2(F)) \to S_p(\ell _2(F))$
with norm less than
 $K$
.
$K$
.
The same equivalence is true for the
![]() $(p_1, \ldots, p_n)-mb$
norms.
$(p_1, \ldots, p_n)-mb$
norms.
Now let
![]() $G$
again be a locally compact group. In general, one has
$G$
again be a locally compact group. In general, one has
![]() $L_p(\mathcal{L} G) \cap S_p(L_2(G)) = \{0\}$
, so we cannot directly link Fourier and Schur multipliers as in the case
$L_p(\mathcal{L} G) \cap S_p(L_2(G)) = \{0\}$
, so we cannot directly link Fourier and Schur multipliers as in the case
![]() $p = \infty$
. In Section 5, we will use the following trick from [Reference Caspers and de la Salle3] to circumvent this difficulty. Let
$p = \infty$
. In Section 5, we will use the following trick from [Reference Caspers and de la Salle3] to circumvent this difficulty. Let
![]() $F \subseteq G$
be a relatively compact Borel subset of
$F \subseteq G$
be a relatively compact Borel subset of
![]() $G$
with positive measure and
$G$
with positive measure and
![]() $P_F\,:\, L_2(G) \to L_2(F)$
,
$P_F\,:\, L_2(G) \to L_2(F)$
,
![]() $f \mapsto 1_F f$
the orthogonal projection. Then for
$f \mapsto 1_F f$
the orthogonal projection. Then for
![]() $x \in L_p(\mathcal{L} G)$
, one can formally define the operator
$x \in L_p(\mathcal{L} G)$
, one can formally define the operator
![]() $P_F x P_F$
, which lies in
$P_F x P_F$
, which lies in
![]() $S_p(L_2(G))$
. We refer to [Reference Caspers and de la Salle3, Proposition 3.3, Theorem5.1] for details.
$S_p(L_2(G))$
. We refer to [Reference Caspers and de la Salle3, Proposition 3.3, Theorem5.1] for details.
Let
![]() $F \subseteq G$
compact. We calculate the kernel of
$F \subseteq G$
compact. We calculate the kernel of
![]() $P_F \Delta ^a \lambda (f) \Delta ^b P_F$
: for
$P_F \Delta ^a \lambda (f) \Delta ^b P_F$
: for
![]() $g \in C_c(G)$
and
$g \in C_c(G)$
and
![]() $s \in G$
, we have
$s \in G$
, we have
 \begin{align*} \begin{split} (P_F \Delta ^a \lambda (f) \Delta ^b P_F g)(s) &= 1_F(s) \Delta ^a(s) \int _G f(t) \Delta ^b(t^{-1} s) 1_F(t^{-1}s) g(t^{-1} s) dt \\ &= 1_F(s) \Delta ^a(s) \int _G f(st) \Delta ^b(t^{-1}) 1_F(t^{-1}) g(t^{-1}) dt \\ &= 1_F(s) \Delta ^a(s) \int _G f(st^{-1}) \Delta ^b(t) 1_F(t) \Delta (t^{-1}) g(t) dt. \end{split} \end{align*}
\begin{align*} \begin{split} (P_F \Delta ^a \lambda (f) \Delta ^b P_F g)(s) &= 1_F(s) \Delta ^a(s) \int _G f(t) \Delta ^b(t^{-1} s) 1_F(t^{-1}s) g(t^{-1} s) dt \\ &= 1_F(s) \Delta ^a(s) \int _G f(st) \Delta ^b(t^{-1}) 1_F(t^{-1}) g(t^{-1}) dt \\ &= 1_F(s) \Delta ^a(s) \int _G f(st^{-1}) \Delta ^b(t) 1_F(t) \Delta (t^{-1}) g(t) dt. \end{split} \end{align*}
Hence the kernel of
![]() $P_F \Delta ^a \lambda (f) \Delta ^b P_F$
is given by
$P_F \Delta ^a \lambda (f) \Delta ^b P_F$
is given by
3. The definition of multilinear Fourier multipliers for non-unimodular groups
In this section,
![]() $G$
is an arbitrary locally compact group. Let
$G$
is an arbitrary locally compact group. Let
![]() $1 \leq p_1, \dots, p_n, p \leq \infty$
with
$1 \leq p_1, \dots, p_n, p \leq \infty$
with
![]() $p^{-1} = \sum _{i=1}^n p_i^{-1}$
and
$p^{-1} = \sum _{i=1}^n p_i^{-1}$
and
![]() $\phi \in L_\infty (G^{\times n})$
. In this section, we explore what a suitable definition for the Fourier multiplier
$\phi \in L_\infty (G^{\times n})$
. In this section, we explore what a suitable definition for the Fourier multiplier
![]() $T_\phi \,:\, L_{p_1}(\mathcal{L} G) \times \ldots L_{p_n}(\mathcal{L} G) \to L_p(\mathcal{L} G)$
might be. Our first requirement is that it must coincide with the linear definition for
$T_\phi \,:\, L_{p_1}(\mathcal{L} G) \times \ldots L_{p_n}(\mathcal{L} G) \to L_p(\mathcal{L} G)$
might be. Our first requirement is that it must coincide with the linear definition for
![]() $n=1$
; that is, it must satisfy (2.8).
$n=1$
; that is, it must satisfy (2.8).
Second, we would like the definition to be compatible with interpolation arguments. More precisely, if
![]() $T_\phi$
is bounded as a map
$T_\phi$
is bounded as a map
![]() $\mathcal{L} G \times \ldots \times \mathcal{L} G \to \mathcal{L} G$
and as a map
$\mathcal{L} G \times \ldots \times \mathcal{L} G \to \mathcal{L} G$
and as a map
![]() $L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_n}(\mathcal{L} G) \to L_p(\mathcal{L} G)$
, then it should also be bounded as map
$L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_n}(\mathcal{L} G) \to L_p(\mathcal{L} G)$
, then it should also be bounded as map
![]() $L_{\frac{p_1}\nu }(\mathcal{L} G) \times \ldots \times L_{\frac{p_n}\nu }(\mathcal{L} G) \to L_{\frac{p}\nu }(\mathcal{L} G)$
for all
$L_{\frac{p_1}\nu }(\mathcal{L} G) \times \ldots \times L_{\frac{p_n}\nu }(\mathcal{L} G) \to L_{\frac{p}\nu }(\mathcal{L} G)$
for all
![]() $0 \lt \nu \lt 1$
. This means that the definition must be ‘compatible’ with the definition on
$0 \lt \nu \lt 1$
. This means that the definition must be ‘compatible’ with the definition on
![]() $(\mathcal{L} G)^{\times n}$
, in the sense that in each input, the maps
$(\mathcal{L} G)^{\times n}$
, in the sense that in each input, the maps
![]() $T_\phi$
must coincide on the intersection space of some compatible couple (with respect to some
$T_\phi$
must coincide on the intersection space of some compatible couple (with respect to some
![]() $\theta$
). This tells us what the Fourier multiplier should look like on the dense subsets
$\theta$
). This tells us what the Fourier multiplier should look like on the dense subsets
![]() ${\kappa }_{p_i}^\theta (L)$
:
${\kappa }_{p_i}^\theta (L)$
:
Definition 3.1 (‘Wrong definition’). Let
![]() $\theta _1, \dots, \theta _n, \theta \in [0,1]$
and
$\theta _1, \dots, \theta _n, \theta \in [0,1]$
and
![]() $x_i ={\kappa }_{p_i}^{\theta _i}(\lambda (f_i))$
for
$x_i ={\kappa }_{p_i}^{\theta _i}(\lambda (f_i))$
for
![]() $i = 1, \dots, n$
, where
$i = 1, \dots, n$
, where
![]() $f_i \in C_c(G) * C_c(G)$
. We set
$f_i \in C_c(G) * C_c(G)$
. We set
Definition 3.1 might seem reasonable at first glance; it coincides with the linear definition for
![]() $n=1$
, and it is the only option if we want interpolation results. However, there are several problems with Definition 3.1. First, the definition depends on the choice of embeddings, which is not an issue in the linear case. Second, there are several properties of multilinear Fourier multipliers on unimodular groups, which do not carry over. This includes, for instance, [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.3 and Lemma 4.4], which are crucial in the proof of the transference from Fourier to Schur multipliers. Moreover, if we want to prove an approximate intertwining property as in (5.1), Corollary 5.5 tells us that the definition of the Fourier multiplier has to ‘preserve products of linear multipliers’, in the sense that
$n=1$
, and it is the only option if we want interpolation results. However, there are several problems with Definition 3.1. First, the definition depends on the choice of embeddings, which is not an issue in the linear case. Second, there are several properties of multilinear Fourier multipliers on unimodular groups, which do not carry over. This includes, for instance, [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.3 and Lemma 4.4], which are crucial in the proof of the transference from Fourier to Schur multipliers. Moreover, if we want to prove an approximate intertwining property as in (5.1), Corollary 5.5 tells us that the definition of the Fourier multiplier has to ‘preserve products of linear multipliers’, in the sense that
whenever
![]() $\phi (s_1, \dots, s_n) = \phi _1(s_1) \ldots \phi _n(s_n)$
. Definition 3.1 does not do this. This means that there is essentially no hope of proving the transference from Schur to Fourier multipliers either.
$\phi (s_1, \dots, s_n) = \phi _1(s_1) \ldots \phi _n(s_n)$
. Definition 3.1 does not do this. This means that there is essentially no hope of proving the transference from Schur to Fourier multipliers either.
The above requirement on the preservation of products leads us to consider instead the following definition. Let
![]() $\theta _i \in [0,1]$
and set
$\theta _i \in [0,1]$
and set
![]() $a_i = \frac{1-\theta _i}{p_i}$
and
$a_i = \frac{1-\theta _i}{p_i}$
and
![]() $b_i = \frac{\theta _i}{p_i}$
so that
$b_i = \frac{\theta _i}{p_i}$
so that
![]() ${\kappa }_{p_i}^{\theta _i}(x) = \Delta ^{a_i} x \Delta ^{b_i}$
. Now for
${\kappa }_{p_i}^{\theta _i}(x) = \Delta ^{a_i} x \Delta ^{b_i}$
. Now for
![]() $f_i \in C_c(G) \star C_c(G)$
, we formally define the Fourier multiplier corresponding to
$f_i \in C_c(G) \star C_c(G)$
, we formally define the Fourier multiplier corresponding to
![]() $\theta _1, \dots, \theta _n$
by
$\theta _1, \dots, \theta _n$
by
 \begin{equation} \begin{split} T_{\phi, (\theta _1, \dots, \theta _n)}({\kappa }^{\theta _1}_{p_1}(\lambda (f_1)),\ldots, {\kappa }^{\theta _n}_{p_n}(\lambda (f_n))) = &\int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \times \\ & \Delta ^{a_1} \lambda _{t_1} \Delta ^{b_1 + a_2} \lambda _{t_2} \ldots \Delta ^{b_{n-1} + a_n} \lambda _{t_n} \Delta ^{b_n} dt_1 \ldots dt_n. \end{split} \end{equation}
\begin{equation} \begin{split} T_{\phi, (\theta _1, \dots, \theta _n)}({\kappa }^{\theta _1}_{p_1}(\lambda (f_1)),\ldots, {\kappa }^{\theta _n}_{p_n}(\lambda (f_n))) = &\int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \times \\ & \Delta ^{a_1} \lambda _{t_1} \Delta ^{b_1 + a_2} \lambda _{t_2} \ldots \Delta ^{b_{n-1} + a_n} \lambda _{t_n} \Delta ^{b_n} dt_1 \ldots dt_n. \end{split} \end{equation}
A priori, it is not clear how to define the integral in (3.2). After all, the integrand
is a function that has unbounded operators as values. However, on closer inspection, the ‘unbounded part’ of this operator doesn’t really depend on the integration variables. Indeed, using the commutation formula (2.3), we can write
 \begin{align*} \begin{split} &H(t_1, \dots, t_n) \\ &\quad= \phi (t_1, \dots, t_n) f_1(t_1) \ldots f_n(t_n) \Delta ^{a_1}(t_1) \Delta ^{a_1 + a_2 + b_1}(t_2) \ldots \Delta ^{\sum _{i=1}^n a_i + \sum _{i=1}^{n-1} b_i}(t_n) \lambda _{t_1\ldots t_n} \Delta ^{1/p} \\ &\quad= \phi (t_1, \dots, t_n) (\Delta ^{\beta _1} f_1)(t_1) \ldots (\Delta ^{\beta _n} f_n)(t_n) \lambda _{t_1\ldots t_n} \cdot \Delta ^{1/p}, \qquad \beta _j = \sum _{i=1}^j a_i + \sum _{i=1}^{j-1} b_i. \\ \end{split} \end{align*}
\begin{align*} \begin{split} &H(t_1, \dots, t_n) \\ &\quad= \phi (t_1, \dots, t_n) f_1(t_1) \ldots f_n(t_n) \Delta ^{a_1}(t_1) \Delta ^{a_1 + a_2 + b_1}(t_2) \ldots \Delta ^{\sum _{i=1}^n a_i + \sum _{i=1}^{n-1} b_i}(t_n) \lambda _{t_1\ldots t_n} \Delta ^{1/p} \\ &\quad= \phi (t_1, \dots, t_n) (\Delta ^{\beta _1} f_1)(t_1) \ldots (\Delta ^{\beta _n} f_n)(t_n) \lambda _{t_1\ldots t_n} \cdot \Delta ^{1/p}, \qquad \beta _j = \sum _{i=1}^j a_i + \sum _{i=1}^{j-1} b_i. \\ \end{split} \end{align*}
Note here that the functions
![]() $\Delta ^{\beta _i} f_i$
are still in
$\Delta ^{\beta _i} f_i$
are still in
![]() $C_c(G) \star C_c(G)$
by (2.5). Hence, a more rigorous way to define the Fourier multiplier is
$C_c(G) \star C_c(G)$
by (2.5). Hence, a more rigorous way to define the Fourier multiplier is
However, we will keep the notation from (3.2). The integral is justified through the above arguments. The latter expression also makes clear that (3.2) takes values in the space of closed densely defined
![]() $(-1/p)$
-homogeneous operators on
$(-1/p)$
-homogeneous operators on
![]() $L_2(G)$
(see [Reference Terp25, III.(19) and Corollary III.34]). Just as in the linear case, it is not clear that (3.2) takes values in
$L_2(G)$
(see [Reference Terp25, III.(19) and Corollary III.34]). Just as in the linear case, it is not clear that (3.2) takes values in
![]() $L_p(\mathcal{L} G)$
in general; this will be part of the assumptions.
$L_p(\mathcal{L} G)$
in general; this will be part of the assumptions.
It turns out that the operator
![]() $T_{\phi, (\theta _1, \dots, \theta _n)}$
in (3.2) does not depend on the choice of
$T_{\phi, (\theta _1, \dots, \theta _n)}$
in (3.2) does not depend on the choice of
![]() $\theta _i$
’s:
$\theta _i$
’s:
Proposition 3.2.
Let
![]() $1 \leq p_1, \dots, p_n, p \lt \infty$
and
$1 \leq p_1, \dots, p_n, p \lt \infty$
and
![]() $\theta _1, \dots, \theta _n \in [0,1]$
. The maps
$\theta _1, \dots, \theta _n \in [0,1]$
. The maps
![]() $T_{\phi, (\theta _1, \dots, \theta _n)}$
and
$T_{\phi, (\theta _1, \dots, \theta _n)}$
and
![]() $T_{\phi, (0,\dots, 0)}$
coincide on the space
$T_{\phi, (0,\dots, 0)}$
coincide on the space
![]() ${\kappa }^0_{p_1}(L) \times \ldots \times{\kappa }^0_{p_n}(L)$
. Consequently, if one of the maps has an image in
${\kappa }^0_{p_1}(L) \times \ldots \times{\kappa }^0_{p_n}(L)$
. Consequently, if one of the maps has an image in
![]() $L_p(\mathcal{L} G)$
and extends continuously to
$L_p(\mathcal{L} G)$
and extends continuously to
![]() $L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_n}(\mathcal{L} G)$
, then the other does as well, and these extensions are equal.
$L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_n}(\mathcal{L} G)$
, then the other does as well, and these extensions are equal.
Proof. Recall that by (2.6),
![]() ${\kappa }_{p_i}^{\theta _i}(L) ={\kappa }_{p_i}^0(L)$
for
${\kappa }_{p_i}^{\theta _i}(L) ={\kappa }_{p_i}^0(L)$
for
![]() $i = 1 \dots, n$
. For any such
$i = 1 \dots, n$
. For any such
![]() $i$
, take
$i$
, take
![]() $a_i, b_i$
as above, that is, so that
$a_i, b_i$
as above, that is, so that
![]() ${\kappa }_{p_i}^\theta (x) = \Delta ^{a_i} x \Delta ^{b_i}$
. Let
${\kappa }_{p_i}^\theta (x) = \Delta ^{a_i} x \Delta ^{b_i}$
. Let
![]() $f_i \in C_c(G) \star C_c(G)$
and set
$f_i \in C_c(G) \star C_c(G)$
and set
![]() $g_i = \Delta ^{-b_i} f_i$
. Then by (2.4),
$g_i = \Delta ^{-b_i} f_i$
. Then by (2.4),
![]() $\Delta ^{a_i} \lambda (f_i) \Delta ^{b_i} = \Delta ^{1/p_1} \lambda (g_i) \,=\!:\, x_i$
, that is,
$\Delta ^{a_i} \lambda (f_i) \Delta ^{b_i} = \Delta ^{1/p_1} \lambda (g_i) \,=\!:\, x_i$
, that is,
![]() ${\kappa }_{p_i}^{\theta _i}(\lambda (f_i)) ={\kappa }_{p_i}^0(\lambda (g_i))$
. By (2.3), we find
${\kappa }_{p_i}^{\theta _i}(\lambda (f_i)) ={\kappa }_{p_i}^0(\lambda (g_i))$
. By (2.3), we find
 \begin{align*} \begin{split} T_{\phi, (\theta _1, \dots, \theta _n)}(x_1, \dots, x_n) = &\int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \times \\ & \Delta ^{a_1} \lambda _{t_1} \Delta ^{b_1 + a_2} \lambda _{t_2} \ldots \Delta ^{b_{n-1} + a_n} \lambda _{t_n} \Delta ^{b_n} dt_1 \ldots dt_n \\ = & \int _{G^{\times n}} \phi (t_1,\ldots, t_n) \Delta ^{-b_1}(t_1) f_1(t_1) \Delta ^{-b_2}(t_2) f_2(t_2) \ldots \Delta ^{-b_n}(t_n)f_n(t_n) \times \\ & \Delta ^{1/p_1} \lambda _{t_1} \Delta ^{1/p_2} \ldots \Delta ^{1/p_n} \lambda _{t_n} dt_1 \ldots dt_n \\ = &T_{\phi, (0, \dots, 0)}(\Delta ^{1/p_1} \lambda (g_1), \dots, \Delta ^{1/p_n} \lambda (g_n)) = T_{\phi, (0, \dots, 0)}(x_1, \dots, x_n). \end{split} \end{align*}
\begin{align*} \begin{split} T_{\phi, (\theta _1, \dots, \theta _n)}(x_1, \dots, x_n) = &\int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \times \\ & \Delta ^{a_1} \lambda _{t_1} \Delta ^{b_1 + a_2} \lambda _{t_2} \ldots \Delta ^{b_{n-1} + a_n} \lambda _{t_n} \Delta ^{b_n} dt_1 \ldots dt_n \\ = & \int _{G^{\times n}} \phi (t_1,\ldots, t_n) \Delta ^{-b_1}(t_1) f_1(t_1) \Delta ^{-b_2}(t_2) f_2(t_2) \ldots \Delta ^{-b_n}(t_n)f_n(t_n) \times \\ & \Delta ^{1/p_1} \lambda _{t_1} \Delta ^{1/p_2} \ldots \Delta ^{1/p_n} \lambda _{t_n} dt_1 \ldots dt_n \\ = &T_{\phi, (0, \dots, 0)}(\Delta ^{1/p_1} \lambda (g_1), \dots, \Delta ^{1/p_n} \lambda (g_n)) = T_{\phi, (0, \dots, 0)}(x_1, \dots, x_n). \end{split} \end{align*}
With this issue out of the way, we can now define Fourier multipliers independent of the choice of
![]() $\theta _i$
’s:
$\theta _i$
’s:
Definition 3.3 (‘Correct definition’). Let
![]() $1 \leq p_1, \dots, p_n, p \leq \infty$
with
$1 \leq p_1, \dots, p_n, p \leq \infty$
with
![]() $p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Also let
$p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Also let
![]() $\phi \in L_\infty (G^{\times n})$
. For
$\phi \in L_\infty (G^{\times n})$
. For
![]() $i = 1, \dots, n$
, take any
$i = 1, \dots, n$
, take any
![]() $a_i, b_i \in [0,1]$
such that
$a_i, b_i \in [0,1]$
such that
![]() $a_i + b_i = p_i^{-1}$
. If the map
$a_i + b_i = p_i^{-1}$
. If the map
which is given for
![]() $x_i = \Delta ^{a_i} \lambda (f_i) \Delta ^{b_i}$
with
$x_i = \Delta ^{a_i} \lambda (f_i) \Delta ^{b_i}$
with
![]() $f_i \in C_c(G) \star C_c(G)$
by
$f_i \in C_c(G) \star C_c(G)$
by
 \begin{equation} \begin{split} T_\phi (x_1,\ldots, x_n) = &\int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \times \\ & \Delta ^{a_1} \lambda _{t_1} \Delta ^{b_1 + a_2} \lambda _{t_2} \ldots \Delta ^{b_{n-1} + a_n} \lambda _{t_n} \Delta ^{b_n} dt_1 \ldots dt_n, \end{split} \end{equation}
\begin{equation} \begin{split} T_\phi (x_1,\ldots, x_n) = &\int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \times \\ & \Delta ^{a_1} \lambda _{t_1} \Delta ^{b_1 + a_2} \lambda _{t_2} \ldots \Delta ^{b_{n-1} + a_n} \lambda _{t_n} \Delta ^{b_n} dt_1 \ldots dt_n, \end{split} \end{equation}
takes values in
![]() $L_p(\mathcal{L} G)$
and extends boundedly to
$L_p(\mathcal{L} G)$
and extends boundedly to
![]() $L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_n}(\mathcal{L} G)$
in the norm topology (in case
$L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_n}(\mathcal{L} G)$
in the norm topology (in case
![]() $p_i = \infty$
for some
$p_i = \infty$
for some
![]() $i$
, we use the space
$i$
, we use the space
![]() $C_\lambda ^*(G)$
instead of
$C_\lambda ^*(G)$
instead of
![]() $L_\infty (\mathcal{L} G) = \mathcal{L} G$
in the
$L_\infty (\mathcal{L} G) = \mathcal{L} G$
in the
![]() $i$
’th leg), then we say that
$i$
’th leg), then we say that
![]() $\phi$
defines a
$\phi$
defines a
![]() $(p_1, \dots, p_n)$
-Fourier multiplier. We denote the extension by
$(p_1, \dots, p_n)$
-Fourier multiplier. We denote the extension by
![]() $T_\phi$
or
$T_\phi$
or
![]() $T_{\phi }^{p_1, \dots, p_n}$
when we wish to emphasise the domain of the operator. This is especially useful when writing an operator norm since writing out the full domain and codomain generally makes equations too long. If
$T_{\phi }^{p_1, \dots, p_n}$
when we wish to emphasise the domain of the operator. This is especially useful when writing an operator norm since writing out the full domain and codomain generally makes equations too long. If
![]() $T_\phi$
is
$T_\phi$
is
![]() $(p_1, \dots, p_n)$
-multiplicatively bounded, then we say that
$(p_1, \dots, p_n)$
-multiplicatively bounded, then we say that
![]() $\phi$
defines a
$\phi$
defines a
![]() $(p_1, \dots, p_n)$
-mb Fourier multiplier.
$(p_1, \dots, p_n)$
-mb Fourier multiplier.
Clearly, for
![]() $n=1$
, Definition 3.3 reduces to (2.8). It does not give the problems that Definition 3.1 does; as we saw already, it does not depend on the choice of embeddings. Moreover, the properties [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.3 and 4.4] do carry over, as we show in Lemmas 3.6 and 3.8. Finally, it preserves products in the following more general way: if
$n=1$
, Definition 3.3 reduces to (2.8). It does not give the problems that Definition 3.1 does; as we saw already, it does not depend on the choice of embeddings. Moreover, the properties [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.3 and 4.4] do carry over, as we show in Lemmas 3.6 and 3.8. Finally, it preserves products in the following more general way: if
![]() $\phi$
is such that there exist
$\phi$
is such that there exist
![]() $m \lt n$
and
$m \lt n$
and
![]() $\phi _1\,:\, G^{\times m} \to{\mathrm{\mathbb{C}}}$
,
$\phi _1\,:\, G^{\times m} \to{\mathrm{\mathbb{C}}}$
,
![]() $\phi _2\,:\, G^{\times n-m} \to{\mathrm{\mathbb{C}}}$
such that
$\phi _2\,:\, G^{\times n-m} \to{\mathrm{\mathbb{C}}}$
such that
then
However, we have to give up interpolation results in general. The only instances where interpolation might work is when the
![]() $L_p$
-spaces ‘in the middle’ are all equal to
$L_p$
-spaces ‘in the middle’ are all equal to
![]() $C_\lambda ^*(G)$
. Indeed, in that case, we can take
$C_\lambda ^*(G)$
. Indeed, in that case, we can take
![]() $\theta _1 = 0$
,
$\theta _1 = 0$
,
![]() $\theta _n = 1$
,
$\theta _n = 1$
,
![]() $\theta = \frac{p}{p_n}$
so that the Fourier multiplier
$\theta = \frac{p}{p_n}$
so that the Fourier multiplier
![]() $T_\phi$
from Definition 3.3 also satisfies (3.1). We note that for
$T_\phi$
from Definition 3.3 also satisfies (3.1). We note that for
![]() $n \gt 2$
and
$n \gt 2$
and
![]() $p_i \lt \infty$
for some
$p_i \lt \infty$
for some
![]() $2 \leq i \leq n-1$
, (3.3) is not of the form (3.1) for any
$2 \leq i \leq n-1$
, (3.3) is not of the form (3.1) for any
![]() $\theta _1, \dots, \theta _n, \theta$
, and hence
$\theta _1, \dots, \theta _n, \theta$
, and hence
![]() $T_\phi$
cannot be a compatible morphism for any ‘usual’ compatible couple structures on
$T_\phi$
cannot be a compatible morphism for any ‘usual’ compatible couple structures on
![]() $(\mathcal{L} G, L_{p_i}(\mathcal{L} G))_{\theta _i}$
.
$(\mathcal{L} G, L_{p_i}(\mathcal{L} G))_{\theta _i}$
.
Remark 3.4.
Although (
3.1
) is a necessary condition for the Fourier multiplier to allow interpolation, we have not been able to prove that it is a sufficient condition. The issue is that to prove that the mapping for
![]() $(p_1, \dots, p_n)$
is compatible with the one for
$(p_1, \dots, p_n)$
is compatible with the one for
![]() $(\infty, \dots, \infty )$
, we have to prove that they coincide on the entire intersection space
$(\infty, \dots, \infty )$
, we have to prove that they coincide on the entire intersection space
![]() $L_p(\mathcal{L} G) \cap \mathcal{L} G$
(within the appropriate compatible couple structure). However, we do not know whether
$L_p(\mathcal{L} G) \cap \mathcal{L} G$
(within the appropriate compatible couple structure). However, we do not know whether
![]() $L$
is dense in this space in the intersection norm. In fact, for
$L$
is dense in this space in the intersection norm. In fact, for
![]() $p \gt 2$
, we do not even know if
$p \gt 2$
, we do not even know if
![]() $\mathcal{T}_\varphi ^2$
is dense in the intersection norm.
$\mathcal{T}_\varphi ^2$
is dense in the intersection norm.
Remark 3.5.
We could have just taken (the extension of) the map
![]() $T_\phi ^{\frac 12, \dots, \frac 12}$
as the definition of our Fourier multiplier. This would have allowed us to skip Proposition 3.2, and all the proofs further on in this paper would still work by approximating only with elements in the central embedding. However, the more general definition allows some flexibility to choose convenient embeddings for notation or to avoid some technicalities (in particular in Lemma 3.6).
$T_\phi ^{\frac 12, \dots, \frac 12}$
as the definition of our Fourier multiplier. This would have allowed us to skip Proposition 3.2, and all the proofs further on in this paper would still work by approximating only with elements in the central embedding. However, the more general definition allows some flexibility to choose convenient embeddings for notation or to avoid some technicalities (in particular in Lemma 3.6).
Let us now prove some properties of the multilinear Fourier multiplier for later use. Lemmas 3.6, 3.7 and 3.8 are used in the proof of Theorem4.1. Here, Lemma 3.6 generalises [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.3], and Lemma 3.8 generalises [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.4]. Since the proofs of these two lemmas require careful bookkeeping with modular functions, we will give the full details. The proof of [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.4] was omitted, but it is not that trivial; our argument fills that gap.
Lemma 3.6.
Let
![]() $1 \leq p_j, p \leq \infty$
and fix some
$1 \leq p_j, p \leq \infty$
and fix some
![]() $1 \leq i \leq n$
. Suppose that
$1 \leq i \leq n$
. Suppose that
![]() $\phi \,:\, G^{\times n} \to{\mathrm{\mathbb{C}}}$
is bounded and measurable and set for
$\phi \,:\, G^{\times n} \to{\mathrm{\mathbb{C}}}$
is bounded and measurable and set for
![]() $r,t,r^{\prime} \in G$
:
$r,t,r^{\prime} \in G$
:
Then
![]() $\phi$
defines a
$\phi$
defines a
![]() $(p_1, \dots, p_n)$
-Fourier multiplier (resp.
$(p_1, \dots, p_n)$
-Fourier multiplier (resp.
![]() $(p_1, \dots, p_n)$
-mb Fourier multiplier) iff
$(p_1, \dots, p_n)$
-mb Fourier multiplier) iff
![]() $\bar{\phi }({\cdot}; r,t,r^{\prime})$
defines a
$\bar{\phi }({\cdot}; r,t,r^{\prime})$
defines a
![]() $(p_1, \dots, p_n)$
-Fourier multiplier (resp.
$(p_1, \dots, p_n)$
-Fourier multiplier (resp.
![]() $(p_1, \dots, p_n)$
-mb Fourier multiplier). In that case, for
$(p_1, \dots, p_n)$
-mb Fourier multiplier). In that case, for
![]() $x_j \in L_{p_j}(\mathcal{L} G)$
,
$x_j \in L_{p_j}(\mathcal{L} G)$
,
Further, we have
and
![]() $(r,t,r^{\prime}) \mapsto T_{\bar{\phi }({\cdot}; r,t,r^{\prime})}$
is strongly continuous. In the multiplicatively bounded case, we have for any
$(r,t,r^{\prime}) \mapsto T_{\bar{\phi }({\cdot}; r,t,r^{\prime})}$
is strongly continuous. In the multiplicatively bounded case, we have for any
![]() $N \geq 1$
$N \geq 1$
as maps
![]() $S_{p_1}^N[L_{p_1}(\mathcal{L} G)] \times \ldots \times S_{p_n}^N[L_{p_n}(\mathcal{L} G)] \to S_p^N[L_p(\mathcal{L} G)]$
, and
$S_{p_1}^N[L_{p_1}(\mathcal{L} G)] \times \ldots \times S_{p_n}^N[L_{p_n}(\mathcal{L} G)] \to S_p^N[L_p(\mathcal{L} G)]$
, and
![]() $(r,t,r^{\prime}) \mapsto T_{\bar{\phi }({\cdot}; r,t,r^{\prime})}^{(N)}$
is strongly continuous.
$(r,t,r^{\prime}) \mapsto T_{\bar{\phi }({\cdot}; r,t,r^{\prime})}^{(N)}$
is strongly continuous.
Proof. It is straightforward to check that for
![]() $s \in G$
,
$s \in G$
,
![]() $f \in C_c(G)$
, we have
$f \in C_c(G)$
, we have
![]() $\lambda _s\lambda (f) = \lambda (\lambda _s(f)) = \lambda (f(s^{-1} {\cdot}))$
; moreover, we have
$\lambda _s\lambda (f) = \lambda (\lambda _s(f)) = \lambda (f(s^{-1} {\cdot}))$
; moreover, we have
We will only make a choice for some of the embeddings and leave the rest open; this is notationally more convenient. Let
![]() $x_j = \Delta ^{a_j} \lambda (f_j) \Delta ^{b_j} \in L_{p_j}(\mathcal{L} G)$
, with
$x_j = \Delta ^{a_j} \lambda (f_j) \Delta ^{b_j} \in L_{p_j}(\mathcal{L} G)$
, with
![]() $f_j \in C_c(G) \star C_c(G)$
and
$f_j \in C_c(G) \star C_c(G)$
and
![]() $a_1=b_i = a_{i+1} = b_n = 0$
(hence
$a_1=b_i = a_{i+1} = b_n = 0$
(hence
![]() $b_1 = \frac 1{p_1}, a_i = \frac 1{p_i}$
, etc). We compute
$b_1 = \frac 1{p_1}, a_i = \frac 1{p_i}$
, etc). We compute
 \begin{align*} \begin{split} &T_{\bar{\phi }({\cdot};r,t,r^{\prime})}(x_1, \dots, x_n) \\&\quad = \int _{G^{\times n}} \bar{\phi }(s_1, \dots, s_n; r,t,r^{\prime}) f_1(s_1) \dots f_n(s_n) \lambda _{s_1} \Delta ^{b_1 + a_2} \lambda _{s_2} \dots \Delta ^{b_{n-1} + a_n}\lambda _{s_n} ds_1 \dots ds_n \\&\quad = \int _{G^{\times n}} \phi (s_1, \dots, s_n) f_1(r^{-1}s_1) \dots \Delta (t)^{-1} f_i(s_it^{-1}) f_{i+1}(ts_{i+1}) \dots \Delta (r^{\prime})^{-1} f_n(s_n (r^{\prime})^{-1}) \times \\ &\qquad \lambda _{r^{-1}s_1} \Delta ^{b_1 + a_2} \dots \Delta ^{b_{i-1} + a_i}\lambda _{s_i s_{i+1}} \Delta ^{b_{i+1}+ a_{i+2}} \dots \Delta ^{b_{n-1} + a_n} \lambda _{s_n (r^{\prime})^{-1}} ds_1 \dots ds_n \\&\quad = \lambda _r^* T_\phi \big (\widetilde{x_1}, x_2, \dots, \widetilde{x_i}, \widetilde{x_{i+1}}, \dots, \widetilde{x_n}\big ) \lambda _{r^{\prime}}^*. \end{split} \end{align*}
\begin{align*} \begin{split} &T_{\bar{\phi }({\cdot};r,t,r^{\prime})}(x_1, \dots, x_n) \\&\quad = \int _{G^{\times n}} \bar{\phi }(s_1, \dots, s_n; r,t,r^{\prime}) f_1(s_1) \dots f_n(s_n) \lambda _{s_1} \Delta ^{b_1 + a_2} \lambda _{s_2} \dots \Delta ^{b_{n-1} + a_n}\lambda _{s_n} ds_1 \dots ds_n \\&\quad = \int _{G^{\times n}} \phi (s_1, \dots, s_n) f_1(r^{-1}s_1) \dots \Delta (t)^{-1} f_i(s_it^{-1}) f_{i+1}(ts_{i+1}) \dots \Delta (r^{\prime})^{-1} f_n(s_n (r^{\prime})^{-1}) \times \\ &\qquad \lambda _{r^{-1}s_1} \Delta ^{b_1 + a_2} \dots \Delta ^{b_{i-1} + a_i}\lambda _{s_i s_{i+1}} \Delta ^{b_{i+1}+ a_{i+2}} \dots \Delta ^{b_{n-1} + a_n} \lambda _{s_n (r^{\prime})^{-1}} ds_1 \dots ds_n \\&\quad = \lambda _r^* T_\phi \big (\widetilde{x_1}, x_2, \dots, \widetilde{x_i}, \widetilde{x_{i+1}}, \dots, \widetilde{x_n}\big ) \lambda _{r^{\prime}}^*. \end{split} \end{align*}
Here
By (3.6), we can write
and similarly
Combining everything together, we conclude
By (2.1), we have
Hence, on the dense subsets of elements
![]() $x_j$
as above, we have
$x_j$
as above, we have
![]() $\|T_{\widetilde{\phi }({\cdot} ;r,t,r^{\prime})}\| \leq \|T_{\phi }\|$
. If we set
$\|T_{\widetilde{\phi }({\cdot} ;r,t,r^{\prime})}\| \leq \|T_{\phi }\|$
. If we set
![]() $\psi = \tilde{\phi }({\cdot}; r,t,r^{\prime})$
, then
$\psi = \tilde{\phi }({\cdot}; r,t,r^{\prime})$
, then
![]() $\tilde{\psi }({\cdot}; r^{-1}, t^{-1}, (r^{\prime})^{-1}) = \phi$
. Hence, applying the above result to
$\tilde{\psi }({\cdot}; r^{-1}, t^{-1}, (r^{\prime})^{-1}) = \phi$
. Hence, applying the above result to
![]() $\tilde{\psi }({\cdot}; r^{-1}, t^{-1}, (r^{\prime})^{-1})$
yields the reverse inequality. By density, we conclude that the first three statements of the lemma hold. By [Reference Junge and Sherman15, Lemma 2.3], the (left or right) multiplication with
$\tilde{\psi }({\cdot}; r^{-1}, t^{-1}, (r^{\prime})^{-1})$
yields the reverse inequality. By density, we conclude that the first three statements of the lemma hold. By [Reference Junge and Sherman15, Lemma 2.3], the (left or right) multiplication with
![]() $\lambda _s$
,
$\lambda _s$
,
![]() $s \in G$
is strongly continuous in
$s \in G$
is strongly continuous in
![]() $s$
. This implies the strong continuity of
$s$
. This implies the strong continuity of
![]() $(r,t,r^{\prime}) \mapsto T_{\tilde{\phi }({\cdot};r,t,r^{\prime})}$
.
$(r,t,r^{\prime}) \mapsto T_{\tilde{\phi }({\cdot};r,t,r^{\prime})}$
.
Now assume
![]() $\phi$
defines a
$\phi$
defines a
![]() $(p_1, \dots, p_n)$
-mb Fourier multiplier and let
$(p_1, \dots, p_n)$
-mb Fourier multiplier and let
![]() $N \geq 1$
. Denote by
$N \geq 1$
. Denote by
![]() $\iota _N$
the
$\iota _N$
the
![]() $N \times N$
-identity matrix. Then by writing out the definitions and using (3.5), we find, for
$N \times N$
-identity matrix. Then by writing out the definitions and using (3.5), we find, for
![]() $x_i \in S_{p_i}^N \otimes L_{p_i}(\mathcal{L} G)$
,
$x_i \in S_{p_i}^N \otimes L_{p_i}(\mathcal{L} G)$
,
 \begin{align*} \begin{split} &T_{\bar{\phi }(\cdot ;r,t,r^{\prime})}^{(N)}(x_1, \dots, x_n) \\&\quad = (\iota _N \otimes \lambda _r^*) T_{\phi }^{(N)}((\iota _N \otimes \lambda _r) x_1, \dots, x_i(\iota _N \otimes \lambda _t), (\iota _N \otimes \lambda _t^*) x_{i+1}, \dots, x^n(\iota _N \otimes \lambda _{r^{\prime}})) (\iota _N \otimes \lambda _{r^{\prime}}^*). \end{split} \end{align*}
\begin{align*} \begin{split} &T_{\bar{\phi }(\cdot ;r,t,r^{\prime})}^{(N)}(x_1, \dots, x_n) \\&\quad = (\iota _N \otimes \lambda _r^*) T_{\phi }^{(N)}((\iota _N \otimes \lambda _r) x_1, \dots, x_i(\iota _N \otimes \lambda _t), (\iota _N \otimes \lambda _t^*) x_{i+1}, \dots, x^n(\iota _N \otimes \lambda _{r^{\prime}})) (\iota _N \otimes \lambda _{r^{\prime}}^*). \end{split} \end{align*}
Hence, by a complete/matrix amplified version of the above arguments, we deduce the last two statements.
Lemma 3.7.
Let
![]() $1 \leq p_j, p \leq \infty$
and fix some
$1 \leq p_j, p \leq \infty$
and fix some
![]() $1 \leq i \leq n$
. Suppose that
$1 \leq i \leq n$
. Suppose that
![]() $\phi \,:\, G^{\times n} \to{\mathrm{\mathbb{C}}}$
defines a
$\phi \,:\, G^{\times n} \to{\mathrm{\mathbb{C}}}$
defines a
![]() $(p_1, \dots, p_n)$
-Fourier multiplier and
$(p_1, \dots, p_n)$
-Fourier multiplier and
![]() $\phi _i\,:\, G \to{\mathrm{\mathbb{C}}}$
defines a
$\phi _i\,:\, G \to{\mathrm{\mathbb{C}}}$
defines a
![]() $p_i$
-Fourier multiplier. Set
$p_i$
-Fourier multiplier. Set
Then
![]() $\bar{\phi }$
defines a
$\bar{\phi }$
defines a
![]() $(p_1, \dots, p_n)$
-Fourier multiplier and for
$(p_1, \dots, p_n)$
-Fourier multiplier and for
![]() $x_j \in L_{p_j}(\mathcal{L} G)$
,
$x_j \in L_{p_j}(\mathcal{L} G)$
,
In particular,
Proof. For
![]() $x_j \in{\kappa }_{p_j}^0(L)$
(or any other embedding), it follows directly from writing out the definitions that (3.7) holds (cf. (2.8)). By density, (3.7) holds for general
$x_j \in{\kappa }_{p_j}^0(L)$
(or any other embedding), it follows directly from writing out the definitions that (3.7) holds (cf. (2.8)). By density, (3.7) holds for general
![]() $x_j \in L_{p_j}(\mathcal{L} G)$
, which implies (3.8), so
$x_j \in L_{p_j}(\mathcal{L} G)$
, which implies (3.8), so
![]() $T_{\bar{\phi }}^{p_1, \dots, p_n}$
is bounded.
$T_{\bar{\phi }}^{p_1, \dots, p_n}$
is bounded.
Lemma 3.8.
Let
![]() $1 \leq p_1, \dots, p_n \leq \infty$
. Let
$1 \leq p_1, \dots, p_n \leq \infty$
. Let
![]() $q_j^{-1} = \sum _{i=j}^n p_i^{-1}$
and suppose that
$q_j^{-1} = \sum _{i=j}^n p_i^{-1}$
and suppose that
![]() $\phi _j\,:\, G \to{\mathrm{\mathbb{C}}}$
defines a
$\phi _j\,:\, G \to{\mathrm{\mathbb{C}}}$
defines a
![]() $q_j$
-Fourier multiplier for
$q_j$
-Fourier multiplier for
![]() $1 \leq j \leq n$
. Set
$1 \leq j \leq n$
. Set
Then
![]() $\bar{\phi }$
defines a
$\bar{\phi }$
defines a
![]() $(p_1, \dots p_n)$
-Fourier multiplier, and for
$(p_1, \dots p_n)$
-Fourier multiplier, and for
![]() $x_i \in L_{p_i}(\mathcal{L} G)$
, we have
$x_i \in L_{p_i}(\mathcal{L} G)$
, we have
Proof. We first show (3.9) on the dense subset
![]() ${\kappa }^0_{p_i}(L) \times \ldots \times{\kappa }^0_{p_n}(L)$
. The lemma then follows from the boundedness of the
${\kappa }^0_{p_i}(L) \times \ldots \times{\kappa }^0_{p_n}(L)$
. The lemma then follows from the boundedness of the
![]() $T_{\phi _i}$
together with Hölder’s inequality.
$T_{\phi _i}$
together with Hölder’s inequality.
We make the slightly stronger claim that for any
![]() $\phi _2, \dots, \phi _n$
as in the assumptions and any
$\phi _2, \dots, \phi _n$
as in the assumptions and any
![]() $x_i \in{\kappa }^0_{p_i}(L)$
, there exists a compactly supported function
$x_i \in{\kappa }^0_{p_i}(L)$
, there exists a compactly supported function
![]() $g\,:\, G \to{\mathrm{\mathbb{C}}}$
such that for all
$g\,:\, G \to{\mathrm{\mathbb{C}}}$
such that for all
![]() $\phi _1$
as in the assumptions,
$\phi _1$
as in the assumptions,
We will prove (3.10) with induction on
![]() $n$
. We will need this intermediate step in order to expand the outer Fourier multiplier in the right-hand side of (3.9).
$n$
. We will need this intermediate step in order to expand the outer Fourier multiplier in the right-hand side of (3.9).
The case
![]() $n=1$
follows directly from (2.8). Now assume that (3.10) holds for any choice of
$n=1$
follows directly from (2.8). Now assume that (3.10) holds for any choice of
![]() $\phi _1, \dots, \phi _{n-1}$
as above and
$\phi _1, \dots, \phi _{n-1}$
as above and
![]() $x_1, \dots, x_{n-1}$
with
$x_1, \dots, x_{n-1}$
with
![]() $x_i \in{\kappa }^0_{p^{\prime}_i}(L)$
. Fix functions
$x_i \in{\kappa }^0_{p^{\prime}_i}(L)$
. Fix functions
![]() $\phi _1, \dots, \phi _n$
as in the assumptions and
$\phi _1, \dots, \phi _n$
as in the assumptions and
![]() $x_1, \dots, x_n$
so that
$x_1, \dots, x_n$
so that
![]() $x_i = \Delta ^{\frac 1{p_i}} \lambda (f_i)$
for
$x_i = \Delta ^{\frac 1{p_i}} \lambda (f_i)$
for
![]() $f_i \in C_c(G) \star C_c(G)$
. Take
$f_i \in C_c(G) \star C_c(G)$
. Take
![]() $g$
compactly supported such that for any
$g$
compactly supported such that for any
![]() $\psi \,:\, G \to{\mathrm{\mathbb{C}}}$
defining a
$\psi \,:\, G \to{\mathrm{\mathbb{C}}}$
defining a
![]() $q_2$
-Fourier multiplier,
$q_2$
-Fourier multiplier,
where
![]() $\bar{\psi }(s_2, \dots, s_n) = \psi (s_2 \ldots s_n) \phi _3(s_3\ldots s_n) \ldots \phi _n(s_n)$
. We calculate
$\bar{\psi }(s_2, \dots, s_n) = \psi (s_2 \ldots s_n) \phi _3(s_3\ldots s_n) \ldots \phi _n(s_n)$
. We calculate
 \begin{align*} \begin{split} T_{\phi _1}(x_1 T_{\phi _2}(x_2 \ldots T_{\phi _n}(x_n)\ldots )) &\stackrel{(3.11)}= T_{\phi _1}(\Delta ^{\frac 1{p_1}} \lambda (f_1) \Delta ^{\frac 1{q_2}} \lambda (\phi _2 g)) \\ &\stackrel{(2.4)}= T_{\phi _1}(\Delta ^{\frac 1{q_1}} \lambda ((\Delta ^{-\frac 1{q_2}} f_1)*(\phi _2g))) \\ &\stackrel{(2.8)}= \Delta ^{\frac 1{q_1}} \lambda (\phi _1 ((\Delta ^{-\frac 1{q_2}} f_1)*(\phi _2g))). \end{split} \end{align*}
\begin{align*} \begin{split} T_{\phi _1}(x_1 T_{\phi _2}(x_2 \ldots T_{\phi _n}(x_n)\ldots )) &\stackrel{(3.11)}= T_{\phi _1}(\Delta ^{\frac 1{p_1}} \lambda (f_1) \Delta ^{\frac 1{q_2}} \lambda (\phi _2 g)) \\ &\stackrel{(2.4)}= T_{\phi _1}(\Delta ^{\frac 1{q_1}} \lambda ((\Delta ^{-\frac 1{q_2}} f_1)*(\phi _2g))) \\ &\stackrel{(2.8)}= \Delta ^{\frac 1{q_1}} \lambda (\phi _1 ((\Delta ^{-\frac 1{q_2}} f_1)*(\phi _2g))). \end{split} \end{align*}
This shows the second equality from (3.10). Continuing the previous equation,
 \begin{align*} \begin{split} T_{\phi _1}(x_1 T_{\phi _2}(x_2 \ldots T_{\phi _n}(x_n)\ldots )) &= \int _G \phi _1(t) \left (\int _G (\Delta ^{-\frac 1{q_2}} f_1)(s_1) (\phi _2g)(s_1^{-1} t) ds_1\right ) \Delta ^{\frac 1{q_1}} \lambda _t dt \\ &= \int _G \int _G \phi _1(s_1t) (\Delta ^{-\frac 1{q_2}} f_1)(s_1) (\phi _2g)(t) \Delta ^{\frac 1{q_1}} \lambda _{s_1t} dt ds_1 \\ &\stackrel{(2.3)}= \int _G f_1(s_1) \Delta ^{\frac 1{p_1}} \lambda _{s_1} \int _G \phi _1(s_1t) \phi _2(t) g(t) \Delta ^{\frac 1{q_2}} \lambda _t dt ds_1 \\ &= \int _G f_1(s_1) \Delta ^{\frac 1{p_1}} \lambda _{s_1} \Delta ^{\frac 1{q_2}} \lambda (\phi _1(s_1 {\cdot}) \phi _2 g) ds_1. \\ \end{split} \end{align*}
\begin{align*} \begin{split} T_{\phi _1}(x_1 T_{\phi _2}(x_2 \ldots T_{\phi _n}(x_n)\ldots )) &= \int _G \phi _1(t) \left (\int _G (\Delta ^{-\frac 1{q_2}} f_1)(s_1) (\phi _2g)(s_1^{-1} t) ds_1\right ) \Delta ^{\frac 1{q_1}} \lambda _t dt \\ &= \int _G \int _G \phi _1(s_1t) (\Delta ^{-\frac 1{q_2}} f_1)(s_1) (\phi _2g)(t) \Delta ^{\frac 1{q_1}} \lambda _{s_1t} dt ds_1 \\ &\stackrel{(2.3)}= \int _G f_1(s_1) \Delta ^{\frac 1{p_1}} \lambda _{s_1} \int _G \phi _1(s_1t) \phi _2(t) g(t) \Delta ^{\frac 1{q_2}} \lambda _t dt ds_1 \\ &= \int _G f_1(s_1) \Delta ^{\frac 1{p_1}} \lambda _{s_1} \Delta ^{\frac 1{q_2}} \lambda (\phi _1(s_1 {\cdot}) \phi _2 g) ds_1. \\ \end{split} \end{align*}
Applying (3.11) again but now with
![]() $\phi _1(s_1 {\cdot}) \phi _2$
in place of
$\phi _1(s_1 {\cdot}) \phi _2$
in place of
![]() $\psi$
, we get
$\psi$
, we get
 \begin{align*} \begin{split} &T_{\phi _1}(x_1 T_{\phi _2}(x_2 \ldots T_{\phi _n}(x_n)\ldots )) \\ &\quad = \int _G f_1(s_1) \Delta ^{\frac 1{p_1}}\lambda _{s_1} \int _{G^{\times n-1}} \phi _1(s_1s_2 \ldots s_n) \phi _2(s_2 \ldots s_n) \phi _3(s_3 \ldots s_n) \ldots \phi _n(s_n) \times \\ & \qquad \qquad \qquad \qquad \qquad \qquad f_2(s_2) \ldots f_n(s_n) \Delta ^{\frac 1{p_2}} \lambda _{s_2} \ldots \Delta ^{\frac 1{p_n}} \lambda _{s_n} ds_2 \ldots ds_n ds_1 \\ &\quad= T_{\bar{\phi }}(x_1, \dots, x_n). \end{split} \end{align*}
\begin{align*} \begin{split} &T_{\phi _1}(x_1 T_{\phi _2}(x_2 \ldots T_{\phi _n}(x_n)\ldots )) \\ &\quad = \int _G f_1(s_1) \Delta ^{\frac 1{p_1}}\lambda _{s_1} \int _{G^{\times n-1}} \phi _1(s_1s_2 \ldots s_n) \phi _2(s_2 \ldots s_n) \phi _3(s_3 \ldots s_n) \ldots \phi _n(s_n) \times \\ & \qquad \qquad \qquad \qquad \qquad \qquad f_2(s_2) \ldots f_n(s_n) \Delta ^{\frac 1{p_2}} \lambda _{s_2} \ldots \Delta ^{\frac 1{p_n}} \lambda _{s_n} ds_2 \ldots ds_n ds_1 \\ &\quad= T_{\bar{\phi }}(x_1, \dots, x_n). \end{split} \end{align*}
Finally, we calculate a convenient form for the kernel of a corner of the Fourier multiplier for use in Theorem 5.1.
Lemma 3.9.
Let
![]() $F \subseteq G$
compact and
$F \subseteq G$
compact and
![]() $x_i = \Delta ^{a_i} \lambda (f_i) \Delta ^{b_i} \in L_{p_i}(\mathcal{L} G)$
as above for
$x_i = \Delta ^{a_i} \lambda (f_i) \Delta ^{b_i} \in L_{p_i}(\mathcal{L} G)$
as above for
![]() $f_i \in C_c(G) \star C_c(G)$
. Then the kernel of
$f_i \in C_c(G) \star C_c(G)$
. Then the kernel of
![]() $P_F T_\phi (x_1, \dots, x_n) P_F$
is given by
$P_F T_\phi (x_1, \dots, x_n) P_F$
is given by
 \begin{align*} \begin{split} (t_0,t_n) \mapsto 1_F(t_0) 1_F(t_n) \int _{G^{\times n-1}} & \phi (t_0t_1^{-1},\ldots, t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) \times \\ & \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \ldots \Delta ^{b_n}(t_n) \Delta ((t_1 \ldots t_n)^{-1}) dt_1\ldots dt_{n-1}. \end{split} \end{align*}
\begin{align*} \begin{split} (t_0,t_n) \mapsto 1_F(t_0) 1_F(t_n) \int _{G^{\times n-1}} & \phi (t_0t_1^{-1},\ldots, t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) \times \\ & \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \ldots \Delta ^{b_n}(t_n) \Delta ((t_1 \ldots t_n)^{-1}) dt_1\ldots dt_{n-1}. \end{split} \end{align*}
Proof. Let
![]() $g \in C_c(G) \star C_c(G)$
and
$g \in C_c(G) \star C_c(G)$
and
![]() $t_0 \in G$
. Then the function
$t_0 \in G$
. Then the function
![]() $P_F T_\phi ^{\theta _1, \dots, \theta _n}(x_1, \dots, x_n) P_F g$
is given by
$P_F T_\phi ^{\theta _1, \dots, \theta _n}(x_1, \dots, x_n) P_F g$
is given by
 \begin{align*} \begin{split} t_0 &\mapsto 1_F(t_0) \int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \times \\ & \qquad (\Delta ^{a_1} \lambda _{t_1} \Delta ^{b_1 + a_2} \lambda _{t_2} \ldots \Delta ^{b_{n-1} + a_n} \lambda _{t_n} \Delta ^{b_n} P_F g)(t_0) dt_1 \ldots dt_n \\ &= 1_F(t_0) \int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1^{-1}t_0) \times \ldots \\ & \qquad \Delta ^{b_{n-1} + a_n}(t_{n-1}^{-1} \dots t_1^{-1} t_0) (\Delta ^{b_n}1_F g)(t_n^{-1} \dots t_1^{-1} t_0) dt_1 \ldots dt_n \\ &= 1_F(t_0) \int _{G^{\times n}} \phi (t_0t_1, t_2, \ldots, t_n) f_1(t_0t_1) f_2(t_2) \ldots f_n(t_n) \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1^{-1}) \times \\ & \qquad \Delta ^{b_2 + a_3}(t_2^{-1} t_1^{-1} ) \ldots \Delta ^{b_{n-1} + a_n}(t_{n-1}^{-1} \dots t_1^{-1}) (\Delta ^{b_n}1_F g)(t_n^{-1} \dots t_1^{-1}) dt_1 \ldots dt_n \\ &= 1_F(t_0) \int _{G^{\times n}} \phi (t_0 t_1^{-1}, t_2,\ldots, t_n) f_1(t_0 t_1^{-1}) f_2(t_2)\ldots f_n(t_n) \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \times \\ & \qquad \Delta ^{b_2 + a_3}(t_2^{-1} t_1) \ldots \Delta ^{b_{n-1} + a_n}(t_{n-1}^{-1} \dots t_2^{-1} t_1) (\Delta ^{b_n}1_F g)(t_n^{-1} \dots t_2^{-1} t_1) \Delta (t_1^{-1}) dt_1 \ldots dt_n \\ &= \ldots \\ &= 1_F(t_0) \int _{G^{\times n}} \phi (t_0 t_1^{-1},\ldots, t_{n-1} t_n^{-1}) f_1(t_0 t_1^{-1})\ldots f_n(t_{n-1} t_n^{-1}) \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \times \ldots \\ & \qquad \Delta ^{b_{n-1} + a_n}(t_{n-1}) (\Delta ^{b_n}1_F g)(t_n) \Delta ((t_1 \ldots t_n)^{-1}) dt_1 \ldots dt_n. \\ \end{split} \end{align*}
\begin{align*} \begin{split} t_0 &\mapsto 1_F(t_0) \int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \times \\ & \qquad (\Delta ^{a_1} \lambda _{t_1} \Delta ^{b_1 + a_2} \lambda _{t_2} \ldots \Delta ^{b_{n-1} + a_n} \lambda _{t_n} \Delta ^{b_n} P_F g)(t_0) dt_1 \ldots dt_n \\ &= 1_F(t_0) \int _{G^{\times n}} \phi (t_1,\ldots, t_n) f_1(t_1)\ldots f_n(t_n) \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1^{-1}t_0) \times \ldots \\ & \qquad \Delta ^{b_{n-1} + a_n}(t_{n-1}^{-1} \dots t_1^{-1} t_0) (\Delta ^{b_n}1_F g)(t_n^{-1} \dots t_1^{-1} t_0) dt_1 \ldots dt_n \\ &= 1_F(t_0) \int _{G^{\times n}} \phi (t_0t_1, t_2, \ldots, t_n) f_1(t_0t_1) f_2(t_2) \ldots f_n(t_n) \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1^{-1}) \times \\ & \qquad \Delta ^{b_2 + a_3}(t_2^{-1} t_1^{-1} ) \ldots \Delta ^{b_{n-1} + a_n}(t_{n-1}^{-1} \dots t_1^{-1}) (\Delta ^{b_n}1_F g)(t_n^{-1} \dots t_1^{-1}) dt_1 \ldots dt_n \\ &= 1_F(t_0) \int _{G^{\times n}} \phi (t_0 t_1^{-1}, t_2,\ldots, t_n) f_1(t_0 t_1^{-1}) f_2(t_2)\ldots f_n(t_n) \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \times \\ & \qquad \Delta ^{b_2 + a_3}(t_2^{-1} t_1) \ldots \Delta ^{b_{n-1} + a_n}(t_{n-1}^{-1} \dots t_2^{-1} t_1) (\Delta ^{b_n}1_F g)(t_n^{-1} \dots t_2^{-1} t_1) \Delta (t_1^{-1}) dt_1 \ldots dt_n \\ &= \ldots \\ &= 1_F(t_0) \int _{G^{\times n}} \phi (t_0 t_1^{-1},\ldots, t_{n-1} t_n^{-1}) f_1(t_0 t_1^{-1})\ldots f_n(t_{n-1} t_n^{-1}) \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \times \ldots \\ & \qquad \Delta ^{b_{n-1} + a_n}(t_{n-1}) (\Delta ^{b_n}1_F g)(t_n) \Delta ((t_1 \ldots t_n)^{-1}) dt_1 \ldots dt_n. \\ \end{split} \end{align*}
It follows that the kernel has the required form.
4. Fourier to Schur transference
Let
![]() $G$
be a locally compact first countable group. In this section, we prove the transference from Fourier to Schur multipliers for such groups. An important ingredient will be the following ‘split’ coordinate-wise convolution: fix functions
$G$
be a locally compact first countable group. In this section, we prove the transference from Fourier to Schur multipliers for such groups. An important ingredient will be the following ‘split’ coordinate-wise convolution: fix functions
![]() $\varphi _k \in C_c(G) \star C_c(G) \subseteq A(G)$
such that
$\varphi _k \in C_c(G) \star C_c(G) \subseteq A(G)$
such that
![]() $\|\varphi _k\|_1 = 1$
and the supports of
$\|\varphi _k\|_1 = 1$
and the supports of
![]() $\varphi _k$
form a decreasing neighbourhood basis of
$\varphi _k$
form a decreasing neighbourhood basis of
![]() $\{e\}$
. In other words,
$\{e\}$
. In other words,
![]() $(\varphi _k)$
is an approximate unit for the Banach
$(\varphi _k)$
is an approximate unit for the Banach
![]() $*$
-algebra
$*$
-algebra
![]() $L_1(G)$
. Note that we use the first countability of
$L_1(G)$
. Note that we use the first countability of
![]() $G$
here. Now, given a bounded function
$G$
here. Now, given a bounded function
![]() $\phi \,:\, G^{\times n} \to{\mathrm{\mathbb{C}}}$
and some fixed
$\phi \,:\, G^{\times n} \to{\mathrm{\mathbb{C}}}$
and some fixed
![]() $1 \leq i \leq n$
, we define
$1 \leq i \leq n$
, we define
and
 \begin{equation} \begin{split} &\phi _k(s_1, \dots, s_n) \,:\!=\, \int _{G^{\times n}} \phi _{t_1, \dots, t_n}(s_1, \dots, s_n) \left ( \prod _{j=1}^n \varphi _k(t_j)\right ) dt_1 \ldots dt_n \\ &\quad = \int _{G^{\times n}} \phi _{t_1, \dots, t_n}(e, \dots, e) \left ( \prod _{j=1}^i \varphi _k(s_j\ldots s_i t_j) \right ) \left ( \prod _{j=i+1}^n \varphi _k(t_js_{i+1} \ldots s_j) \Delta (s_{i+1} \ldots s_j) \right ) dt_1 \ldots dt_n. \end{split} \end{equation}
\begin{equation} \begin{split} &\phi _k(s_1, \dots, s_n) \,:\!=\, \int _{G^{\times n}} \phi _{t_1, \dots, t_n}(s_1, \dots, s_n) \left ( \prod _{j=1}^n \varphi _k(t_j)\right ) dt_1 \ldots dt_n \\ &\quad = \int _{G^{\times n}} \phi _{t_1, \dots, t_n}(e, \dots, e) \left ( \prod _{j=1}^i \varphi _k(s_j\ldots s_i t_j) \right ) \left ( \prod _{j=i+1}^n \varphi _k(t_js_{i+1} \ldots s_j) \Delta (s_{i+1} \ldots s_j) \right ) dt_1 \ldots dt_n. \end{split} \end{equation}
The last term of (4.1) in combination with Lemma 3.8 will allow us to reduce the problem to the linear case. The necessity of the ‘split’ between indices
![]() $i$
and
$i$
and
![]() $i+1$
will be explained later.
$i+1$
will be explained later.
Theorem 4.1.
Let
![]() $G$
be a locally compact first countable group, and let
$G$
be a locally compact first countable group, and let
![]() $1 \leq p \leq \infty$
,
$1 \leq p \leq \infty$
,
![]() $1\lt p_1, \ldots, p_{n-1} \leq \infty$
be such that
$1\lt p_1, \ldots, p_{n-1} \leq \infty$
be such that
![]() $p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
$p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
![]() $\phi \in C_b(G^{\times n})$
and define
$\phi \in C_b(G^{\times n})$
and define
![]() $\widetilde{\phi } \in C_b(G^{\times n + 1})$
by
$\widetilde{\phi } \in C_b(G^{\times n + 1})$
by
If
![]() $\phi$
is defines a
$\phi$
is defines a
![]() $(p_1, \ldots, p_n)$
-mb Fourier multiplier
$(p_1, \ldots, p_n)$
-mb Fourier multiplier
![]() $T_\phi$
of
$T_\phi$
of
![]() $G$
, then
$G$
, then
![]() $\widetilde{\phi }$
defines a
$\widetilde{\phi }$
defines a
![]() $(p_1, \ldots, p_n)$
-mb Schur multiplier
$(p_1, \ldots, p_n)$
-mb Schur multiplier
![]() $M_{\widetilde{\phi }}$
of
$M_{\widetilde{\phi }}$
of
![]() $G$
. Moreover,
$G$
. Moreover,
Proof. Let
![]() $F \subseteq G$
finite with
$F \subseteq G$
finite with
![]() $|F| = N$
. By Theorem 2.2, it suffices to show that the norm of
$|F| = N$
. By Theorem 2.2, it suffices to show that the norm of
and its matrix amplifications are bounded.
For
![]() $s \in F$
, let
$s \in F$
, let
![]() $p_s \in B(\ell _2(F))$
be the orthogonal projection onto the span of
$p_s \in B(\ell _2(F))$
be the orthogonal projection onto the span of
![]() $\delta _s$
. Define the unitary
$\delta _s$
. Define the unitary
![]() $U = \sum _{s \in F} p_s \otimes \lambda _s \in B(\ell _2(F)) \otimes \mathcal{L} G$
. In the case
$U = \sum _{s \in F} p_s \otimes \lambda _s \in B(\ell _2(F)) \otimes \mathcal{L} G$
. In the case
![]() $p = \infty$
, the Fourier to Schur transference is proven through the transference identity
$p = \infty$
, the Fourier to Schur transference is proven through the transference identity
The idea is to do something similar in the case
![]() $p \lt \infty$
. However, the unit does not embed in
$p \lt \infty$
. However, the unit does not embed in
![]() $L_p(\mathcal{L} G)$
, so we need to use some approximation of the unit instead. We construct this as follows: let
$L_p(\mathcal{L} G)$
, so we need to use some approximation of the unit instead. We construct this as follows: let
![]() $\mathcal{V} = (V_i)_{i \in{\operatorname{\mathbb{N}}}}$
be a decreasing symmetric neighbourhood basis of the identity (this is possible because
$\mathcal{V} = (V_i)_{i \in{\operatorname{\mathbb{N}}}}$
be a decreasing symmetric neighbourhood basis of the identity (this is possible because
![]() $G$
is first countable). For
$G$
is first countable). For
![]() $V \in \mathcal{V}$
, we define the operator
$V \in \mathcal{V}$
, we define the operator
which is proven to be self-adjoint in [Reference Caspers, Parcet, Perrin and Ricard8, Section 8.3]. Let
![]() $k_V = u_V h_V$
be its polar decomposition. Then we have
$k_V = u_V h_V$
be its polar decomposition. Then we have
![]() $h_V^{2/p} \in L_p(\mathcal{L} G)$
, and by (2.2),
$h_V^{2/p} \in L_p(\mathcal{L} G)$
, and by (2.2),
![]() $\|h_V^{2/p}\|_p = 1$
. Now for any
$\|h_V^{2/p}\|_p = 1$
. Now for any
![]() $V \in \mathcal{V}$
, we have, by (2.7),
$V \in \mathcal{V}$
, we have, by (2.7),
Next, fix an
![]() $i \in \{1, \dots, n\}$
such that
$i \in \{1, \dots, n\}$
such that
![]() $\bar{p}_1 \,:\!=\, \left (\sum _{l=1}^i p_l^{-1}\right )^{-1} \gt 1$
and
$\bar{p}_1 \,:\!=\, \left (\sum _{l=1}^i p_l^{-1}\right )^{-1} \gt 1$
and
![]() $\bar{p}_2 \,:\!=\, \left (\sum _{l=i+1}^n p_l^{-1}\right )^{-1} \gt 1$
. This is possible by our assumption that
$\bar{p}_2 \,:\!=\, \left (\sum _{l=i+1}^n p_l^{-1}\right )^{-1} \gt 1$
. This is possible by our assumption that
![]() $p_1, \dots, p_n \gt 1$
. We now define the functions
$p_1, \dots, p_n \gt 1$
. We now define the functions
![]() $\phi _{t_1, \dots, t_n}$
and
$\phi _{t_1, \dots, t_n}$
and
![]() $\phi _k$
as in (4.1) for the chosen
$\phi _k$
as in (4.1) for the chosen
![]() $i$
.
$i$
.
The condition
![]() $\bar{p}_1, \bar{p}_2 \gt 1$
is necessary for the use of Proposition 4.3 at the end of the proof of Lemma 4.2; this also explains why we need the ‘split’ in the pointwise convolutions. If
$\bar{p}_1, \bar{p}_2 \gt 1$
is necessary for the use of Proposition 4.3 at the end of the proof of Lemma 4.2; this also explains why we need the ‘split’ in the pointwise convolutions. If
![]() $p\gt 1$
, then one can take
$p\gt 1$
, then one can take
![]() $i=n$
in which case the proof of Lemma 4.2 simplifies somewhat. Note that in [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5] and [Reference Caspers, Krishnaswamy-Usha and Vos6], the convolutions were defined for
$i=n$
in which case the proof of Lemma 4.2 simplifies somewhat. Note that in [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5] and [Reference Caspers, Krishnaswamy-Usha and Vos6], the convolutions were defined for
![]() $i = n-1$
. In the latter paper, this creates a problem in case
$i = n-1$
. In the latter paper, this creates a problem in case
![]() $p_n = \infty, p = 1$
; this problem is resolved by splitting instead at some
$p_n = \infty, p = 1$
; this problem is resolved by splitting instead at some
![]() $i$
chosen as above.
$i$
chosen as above.
Let
![]() $a_1, \ldots, a_n \in B(\ell _2(F))$
. By continuity of
$a_1, \ldots, a_n \in B(\ell _2(F))$
. By continuity of
![]() $\phi$
, we have that
$\phi$
, we have that
![]() $\phi _k \to \phi$
pointwise. Indeed, for
$\phi _k \to \phi$
pointwise. Indeed, for
![]() $\varepsilon \gt 0$
, we can take
$\varepsilon \gt 0$
, we can take
![]() $K$
such that for
$K$
such that for
![]() $t_1, \dots, t_n \in \mathrm{supp} \varphi _K$
,
$t_1, \dots, t_n \in \mathrm{supp} \varphi _K$
,
![]() $|\phi _{t_1, \dots, t_n}(s_1, \dots, s_n) - \phi (s_1, \dots, s_n)| \lt \varepsilon$
. Then for
$|\phi _{t_1, \dots, t_n}(s_1, \dots, s_n) - \phi (s_1, \dots, s_n)| \lt \varepsilon$
. Then for
![]() $k \gt K$
, we get
$k \gt K$
, we get
![]() $|\phi _k(s_1, \dots, s_n) - \phi (s_1, \dots, s_n)| \lt \varepsilon$
. Since we are working in finite dimensions, this implies
$|\phi _k(s_1, \dots, s_n) - \phi (s_1, \dots, s_n)| \lt \varepsilon$
. Since we are working in finite dimensions, this implies
in
![]() $S^N_p$
. Together with (4.2), we find
$S^N_p$
. Together with (4.2), we find
 \begin{align*} \begin{split} \|M_{\widetilde{\phi }}(a_1, \dots, a_n)\|_{S_p^N} &= \lim _k \limsup _{V \in \mathcal{V}} \|M_{\widetilde{\phi _k}}(a_1, \dots, a_n) \otimes h_V^{\frac 2p}\|_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &= \lim _k \limsup _{V \in \mathcal{V}} \|U(M_{\widetilde{\phi _k}}(a_1, \dots, a_n) \otimes h_V^{\frac 2p})U^*\|_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &\leq \limsup _k \limsup _{V \in \mathcal{V}} \|T_{\phi _k}^{(N)}(U(a_1 \otimes h_V^{\frac 2{p_1}})U^*, \ldots, U(a_n \otimes h_V^{\frac 2{p_n}})U^*)\|_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &\quad + \limsup _k \limsup _{V \in \mathcal{V}} \|T_{\phi _k}^{(N)}(U(a_1 \otimes h_V^{\frac 2{p_1}})U^*, \ldots, U(a_n \otimes h_V^{\frac 2{p_n}})U^*) \\ &\qquad \qquad \qquad \qquad \qquad - U(M_{\widetilde{\phi _k}}(a_1, \dots, a_n) \otimes h_V^{\frac 2p})U^*\|_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &\,:\!=\, A + B. \end{split} \end{align*}
\begin{align*} \begin{split} \|M_{\widetilde{\phi }}(a_1, \dots, a_n)\|_{S_p^N} &= \lim _k \limsup _{V \in \mathcal{V}} \|M_{\widetilde{\phi _k}}(a_1, \dots, a_n) \otimes h_V^{\frac 2p}\|_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &= \lim _k \limsup _{V \in \mathcal{V}} \|U(M_{\widetilde{\phi _k}}(a_1, \dots, a_n) \otimes h_V^{\frac 2p})U^*\|_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &\leq \limsup _k \limsup _{V \in \mathcal{V}} \|T_{\phi _k}^{(N)}(U(a_1 \otimes h_V^{\frac 2{p_1}})U^*, \ldots, U(a_n \otimes h_V^{\frac 2{p_n}})U^*)\|_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &\quad + \limsup _k \limsup _{V \in \mathcal{V}} \|T_{\phi _k}^{(N)}(U(a_1 \otimes h_V^{\frac 2{p_1}})U^*, \ldots, U(a_n \otimes h_V^{\frac 2{p_n}})U^*) \\ &\qquad \qquad \qquad \qquad \qquad - U(M_{\widetilde{\phi _k}}(a_1, \dots, a_n) \otimes h_V^{\frac 2p})U^*\|_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &\,:\!=\, A + B. \end{split} \end{align*}
First, we have
 \begin{align*} \begin{split} A &\leq \limsup _k \limsup _{V \in \mathcal{V}} \|T_{\phi _k}^{(N)} \| \|a_1 \otimes h_V^{\frac 2{p_1}}\|_{S_{p_1}^N \otimes L_{p_1}(\mathcal{L} G)} \ldots \|a_n \otimes h_V^{\frac 2{p_n}}\|_{S_{p_n}^N \otimes L_{p_n}(\mathcal{L} G)} \\ &= \limsup _k \|T_{\phi _k}^{(N)}\| \|a_1\|_{S_{p_1}^N} \ldots \|a_n\|_{S_{p_n}^N}. \end{split} \end{align*}
\begin{align*} \begin{split} A &\leq \limsup _k \limsup _{V \in \mathcal{V}} \|T_{\phi _k}^{(N)} \| \|a_1 \otimes h_V^{\frac 2{p_1}}\|_{S_{p_1}^N \otimes L_{p_1}(\mathcal{L} G)} \ldots \|a_n \otimes h_V^{\frac 2{p_n}}\|_{S_{p_n}^N \otimes L_{p_n}(\mathcal{L} G)} \\ &= \limsup _k \|T_{\phi _k}^{(N)}\| \|a_1\|_{S_{p_1}^N} \ldots \|a_n\|_{S_{p_n}^N}. \end{split} \end{align*}
By repeated use of Lemma 3.6 (in particular, we can use Fubini because of the strong continuity property) we find
 \begin{equation*} \|T_{\phi _k}^{(N)}\| \leq \int _{G^{\times n}} \|T_\phi ^{(N)}\| \left ( \prod _{i=1}^n |\varphi _k(t_j)| \right ) dt_1 \ldots dt_n = \|T_\phi ^{(N)}\| \|\varphi _k\|_1^n = \|T_\phi ^{(N)}\| \leq \|T_\phi \|_{(p_1, \dots, p_n)-mb}. \end{equation*}
\begin{equation*} \|T_{\phi _k}^{(N)}\| \leq \int _{G^{\times n}} \|T_\phi ^{(N)}\| \left ( \prod _{i=1}^n |\varphi _k(t_j)| \right ) dt_1 \ldots dt_n = \|T_\phi ^{(N)}\| \|\varphi _k\|_1^n = \|T_\phi ^{(N)}\| \leq \|T_\phi \|_{(p_1, \dots, p_n)-mb}. \end{equation*}
and hence
It remains to show that
![]() $B = 0$
. By the triangle inequality, it suffices to show this for
$B = 0$
. By the triangle inequality, it suffices to show this for
![]() $a_i = E_{r_{i-1}, r_i}$
,
$a_i = E_{r_{i-1}, r_i}$
,
![]() $r_0, \dots, r_n \in F$
(for other combinations of matrix units, the term below becomes 0). In that case we get, by applying Lemma 3.6 in the second equality:
$r_0, \dots, r_n \in F$
(for other combinations of matrix units, the term below becomes 0). In that case we get, by applying Lemma 3.6 in the second equality:
 \begin{align*} \begin{split} & T_{\phi _k}^{(N)}(U(E_{r_0, r_1} \otimes h_V^{\frac 2{p_1}})U^*, \ldots, U(E_{r_{n-1},r_n} \otimes h_V^{\frac 2{p_n}})U^*) - U(M_{\widetilde{\phi _k}}(E_{r_0, r_1}, \dots, E_{r_{n-1},r_n}) \otimes h_V^{\frac 2p})U^*\\ &\quad= E_{r_0, r_n} \otimes \left ( T_{\phi _k}(\lambda _{r_0}h_V^{\frac 2{p_1}} \lambda _{r_1}^*, \ldots, \lambda _{r_{n-1}}h_V^{\frac 2{p_n}} \lambda _{r_n}^*) - \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) \lambda _{r_0} h_V^{\frac 2p}\lambda _{r_n}^* \right ) \\ &\quad = E_{r_0, r_n} \otimes \lambda _{r_0} \left ( T_{\phi _k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p} \right ) \lambda _{r_n}^*. \end{split} \end{align*}
\begin{align*} \begin{split} & T_{\phi _k}^{(N)}(U(E_{r_0, r_1} \otimes h_V^{\frac 2{p_1}})U^*, \ldots, U(E_{r_{n-1},r_n} \otimes h_V^{\frac 2{p_n}})U^*) - U(M_{\widetilde{\phi _k}}(E_{r_0, r_1}, \dots, E_{r_{n-1},r_n}) \otimes h_V^{\frac 2p})U^*\\ &\quad= E_{r_0, r_n} \otimes \left ( T_{\phi _k}(\lambda _{r_0}h_V^{\frac 2{p_1}} \lambda _{r_1}^*, \ldots, \lambda _{r_{n-1}}h_V^{\frac 2{p_n}} \lambda _{r_n}^*) - \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) \lambda _{r_0} h_V^{\frac 2p}\lambda _{r_n}^* \right ) \\ &\quad = E_{r_0, r_n} \otimes \lambda _{r_0} \left ( T_{\phi _k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p} \right ) \lambda _{r_n}^*. \end{split} \end{align*}
Hence,
The limit over
![]() $k$
exists and is 0; we postpone the proof to Lemma 4.2 below.
$k$
exists and is 0; we postpone the proof to Lemma 4.2 below.
For the multiplicatively bounded estimate, we prove using similar methods that for
![]() $K \geq 1$
and
$K \geq 1$
and
![]() $a_1, \dots, a_n \in M_K(B(\ell _2(F)))$
,
$a_1, \dots, a_n \in M_K(B(\ell _2(F)))$
,
Here, we use
![]() $1_{M_K} \otimes U$
in place of
$1_{M_K} \otimes U$
in place of
![]() $U$
. Moreover, by the triangle inequality, it suffices to prove the estimate for
$U$
. Moreover, by the triangle inequality, it suffices to prove the estimate for
![]() $B$
for
$B$
for
![]() $a_i = E_{j_{i-1},j_i} \otimes E_{r_{i-1},r_i}$
, with
$a_i = E_{j_{i-1},j_i} \otimes E_{r_{i-1},r_i}$
, with
![]() $1 \leq j_i \leq K$
and
$1 \leq j_i \leq K$
and
![]() $r_i \in F$
; the expression for
$r_i \in F$
; the expression for
![]() $B$
then reduces to (4.3) again.
$B$
then reduces to (4.3) again.
The following Lemma is similar to [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.6]. In our case, we have
![]() $x_j = 1$
, which allows us to avoid the SAIN condition used in that paper; on the other hand, we work with translated functions, and our result works for non-unimodular groups. Already in [Reference Caspers, Krishnaswamy-Usha and Vos6, Theorem 3.1], it was explained how to adapt the proof of [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.6] for the translated functions. However, this paper only considered unimodular groups. Here, we spell out the full proof for the convenience of the reader.
$x_j = 1$
, which allows us to avoid the SAIN condition used in that paper; on the other hand, we work with translated functions, and our result works for non-unimodular groups. Already in [Reference Caspers, Krishnaswamy-Usha and Vos6, Theorem 3.1], it was explained how to adapt the proof of [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Lemma 4.6] for the translated functions. However, this paper only considered unimodular groups. Here, we spell out the full proof for the convenience of the reader.
Lemma 4.2. In the proof of Theorem 4.1 , we have that
The main idea is to reduce the problem to the linear case using (4.1) and apply the following result for linear Fourier multipliers:
Proposition 4.3.
Let
![]() $\mathcal{V}$
be a symmetric neighbourhood basis of the identity of
$\mathcal{V}$
be a symmetric neighbourhood basis of the identity of
![]() $G$
. Let
$G$
. Let
![]() $2 \leq q \lt p \leq \infty$
or
$2 \leq q \lt p \leq \infty$
or
![]() $1 \leq p \lt q \leq 2$
. Assume
$1 \leq p \lt q \leq 2$
. Assume
![]() $\psi \in C_b(G)$
defines a Fourier multiplier on
$\psi \in C_b(G)$
defines a Fourier multiplier on
![]() $L_p(\mathcal{L} G)$
. Then we have
$L_p(\mathcal{L} G)$
. Then we have
The proof of Proposition 4.3 is essentially a matter of combining results and remarks from [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Proposition 3.9] and [Reference Caspers, Parcet, Perrin and Ricard8, Claim B and Section 8] and applying Haagerup reduction to [Reference Conde-Alonso, Parcet and Ricard9, Lemma 3.1] to generalise that estimate to general von Neumann algebras. We give more details in Section 6.
Proof of Lemma 4.2. The idea is to use a dominated convergence argument in the last expression of (4.1). However, the functions
![]() $\phi _k$
need not be integrable. We work around this by multiplying with compactly supported functions that are close to 1 around
$\phi _k$
need not be integrable. We work around this by multiplying with compactly supported functions that are close to 1 around
![]() $e$
so that as
$e$
so that as
![]() $V \in \mathcal{V}$
decreases to
$V \in \mathcal{V}$
decreases to
![]() $\{e\}$
, we are just ‘multiplying by 1’ in the limit. Define a function
$\{e\}$
, we are just ‘multiplying by 1’ in the limit. Define a function
![]() $\zeta \in C_c(G) \cap A(G)$
with
$\zeta \in C_c(G) \cap A(G)$
with
![]() $\zeta (e) = 1$
, which is positive definite and (therefore) satisfies
$\zeta (e) = 1$
, which is positive definite and (therefore) satisfies
![]() $\|T_{\zeta }\,:\, L_p(\mathcal{L} G) \to L_p(\mathcal{L} G)\| \leq 1$
for all
$\|T_{\zeta }\,:\, L_p(\mathcal{L} G) \to L_p(\mathcal{L} G)\| \leq 1$
for all
![]() $1 \leq p \leq \infty$
. Next let
$1 \leq p \leq \infty$
. Next let
We define a product function as follows:
Then
 \begin{align*} &\| T_{\phi _k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\quad\leq \| (\phi (\zeta _1, \dots, \zeta _n))_k (r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p}- \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\qquad + \| T_{(\phi (\zeta _1, \dots, \zeta _n))_k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - (\phi (\zeta _1, \dots, \zeta _n))_k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\qquad + \|T_{\phi _k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - T_{(\phi (\zeta _1, \dots, \zeta _n))_k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) \|_{L_p(\mathcal{L} G)} \\&\quad \,=\!:\,\ A_{k,V} + B_{k,V} + C_{k,V}. \end{align*}
\begin{align*} &\| T_{\phi _k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\quad\leq \| (\phi (\zeta _1, \dots, \zeta _n))_k (r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p}- \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\qquad + \| T_{(\phi (\zeta _1, \dots, \zeta _n))_k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - (\phi (\zeta _1, \dots, \zeta _n))_k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\qquad + \|T_{\phi _k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - T_{(\phi (\zeta _1, \dots, \zeta _n))_k(r_0 {\cdot} r_1^{-1}, \ldots, r_{n-1} {\cdot} r_n^{-1})}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) \|_{L_p(\mathcal{L} G)} \\&\quad \,=\!:\,\ A_{k,V} + B_{k,V} + C_{k,V}. \end{align*}
Here,
![]() $\phi ((\zeta _1, \dots, \zeta _n))_k$
is defined again by (4.1) for the same
$\phi ((\zeta _1, \dots, \zeta _n))_k$
is defined again by (4.1) for the same
![]() $i$
. We will estimate these terms separately. We start by showing that
$i$
. We will estimate these terms separately. We start by showing that
![]() $\lim _k \limsup _{V \in \mathcal{V}} A_{k,V}$
and
$\lim _k \limsup _{V \in \mathcal{V}} A_{k,V}$
and
![]() $\lim _k \limsup _{V \in \mathcal{V}} C_{k,V}$
are 0, essentially reducing the problem to the integrable functions
$\lim _k \limsup _{V \in \mathcal{V}} C_{k,V}$
are 0, essentially reducing the problem to the integrable functions
![]() $\phi (\zeta _1, \dots, \zeta _n)$
. We then apply the idea mentioned above to show that
$\phi (\zeta _1, \dots, \zeta _n)$
. We then apply the idea mentioned above to show that
![]() $\lim _{V \in \mathcal{V}} B_{k,V} = 0$
for any
$\lim _{V \in \mathcal{V}} B_{k,V} = 0$
for any
![]() $k$
.
$k$
.
First, since
![]() $\psi _k \to \psi$
pointwise for any
$\psi _k \to \psi$
pointwise for any
![]() $\psi \in C_b(G)^{\times n}$
, we have
$\psi \in C_b(G)^{\times n}$
, we have
 \begin{align*} \begin{split} \limsup _{V \in \mathcal{V}} A_{k,V} &= |(\phi (\zeta _1, \dots, \zeta _n))_k (r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) - \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1})|\\ &\to |\phi (r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1})(1 - \zeta _1(r_0r_1^{-1}) \ldots \zeta _n(r_{n-1} r_n^{-1}))| = 0. \end{split} \end{align*}
\begin{align*} \begin{split} \limsup _{V \in \mathcal{V}} A_{k,V} &= |(\phi (\zeta _1, \dots, \zeta _n))_k (r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1}) - \phi _k(r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1})|\\ &\to |\phi (r_0r_1^{-1}, \ldots, r_{n-1}r_n^{-1})(1 - \zeta _1(r_0r_1^{-1}) \ldots \zeta _n(r_{n-1} r_n^{-1}))| = 0. \end{split} \end{align*}
Next, we estimate the limit in
![]() $k$
of
$k$
of
![]() $\limsup _{V \in \mathcal{V}} C_{k,V}$
. Set
$\limsup _{V \in \mathcal{V}} C_{k,V}$
. Set
![]() $u_j = t_j^{-1} r_{j-1}$
,
$u_j = t_j^{-1} r_{j-1}$
,
![]() $v_j = t_j r_j$
and
$v_j = t_j r_j$
and
where
Thanks to the strong continuity statement of Lemma 3.6, we can use Fubini to deduce
 \begin{equation} C_{k,V} \leq \int _{G^{\times n}} C_V(t_1, \dots, t_n) \left (\prod _{i=1}^n |\varphi _k(t_j)|\right ) dt_1 \ldots dt_n. \end{equation}
\begin{equation} C_{k,V} \leq \int _{G^{\times n}} C_V(t_1, \dots, t_n) \left (\prod _{i=1}^n |\varphi _k(t_j)|\right ) dt_1 \ldots dt_n. \end{equation}
Now set
 \begin{align*} \begin{split} &y_{j,V} = \lambda _{u_j}h_V^{\frac 2{p_j}} \lambda _{u_{j+1}}^*\ \text{for } 1 \leq j \leq i-1, \qquad y_{i,V} = \lambda _{u_i} h_V^{\frac 2{p_i}} \lambda _{r_i}^*, \qquad \quad y_{i+1,V} = \lambda _{r_i} h_V^{\frac 2{p_{i+1}}} \lambda _{v_{i+1}}^*, \\ &y_{j,V} = \lambda _{v_{j-1}}h_V^{\frac 2{p_j}} \lambda _{v_j}^* \quad \text{for } i+2 \leq j \leq n. \end{split} \end{align*}
\begin{align*} \begin{split} &y_{j,V} = \lambda _{u_j}h_V^{\frac 2{p_j}} \lambda _{u_{j+1}}^*\ \text{for } 1 \leq j \leq i-1, \qquad y_{i,V} = \lambda _{u_i} h_V^{\frac 2{p_i}} \lambda _{r_i}^*, \qquad \quad y_{i+1,V} = \lambda _{r_i} h_V^{\frac 2{p_{i+1}}} \lambda _{v_{i+1}}^*, \\ &y_{j,V} = \lambda _{v_{j-1}}h_V^{\frac 2{p_j}} \lambda _{v_j}^* \quad \text{for } i+2 \leq j \leq n. \end{split} \end{align*}
Denote
![]() $\iota _q$
for the identity operator on
$\iota _q$
for the identity operator on
![]() $L_q(\mathcal{L} G)$
. The symbol
$L_q(\mathcal{L} G)$
. The symbol
![]() $1$
is used both for the constant 1-function and the number 1. Then we get the following estimate, where we apply Lemma 3.6 and (2.1) in the first line and Lemma 3.7 and the assumption that
$1$
is used both for the constant 1-function and the number 1. Then we get the following estimate, where we apply Lemma 3.6 and (2.1) in the first line and Lemma 3.7 and the assumption that
![]() $T_\zeta$
is a contraction in the third line:
$T_\zeta$
is a contraction in the third line:
 \begin{equation} \begin{split} C_V(t_1, \dots, t_n) &= \|T_{(\phi - \phi (\zeta _1, \dots, \zeta _n))}(y_{1,V}, \dots, y_{n,V})\|_{L_p(\mathcal{L} G)}\\ &\leq \sum _{j=1}^n \|T_{\phi (1, \dots, 1, (\zeta _j - 1), \zeta _{j+1}, \dots, \zeta _n)}(y_{1,V}, \dots, y_{n,V}) \|_{L_p(\mathcal{L} G)} \\ &\leq \|T_{\phi }\,:\, L_{p_1} \times \ldots \times L_{p_n} \to L_p\| \sum _{j=1}^n\left ( \|(T_{\zeta _j} - \iota _{p_j})(y_{j,V})\|_{L_{p_j}(\mathcal{L} G)} \prod _{i \neq j} \|y_{i,V}\|_{p_i}\right ). \end{split} \end{equation}
\begin{equation} \begin{split} C_V(t_1, \dots, t_n) &= \|T_{(\phi - \phi (\zeta _1, \dots, \zeta _n))}(y_{1,V}, \dots, y_{n,V})\|_{L_p(\mathcal{L} G)}\\ &\leq \sum _{j=1}^n \|T_{\phi (1, \dots, 1, (\zeta _j - 1), \zeta _{j+1}, \dots, \zeta _n)}(y_{1,V}, \dots, y_{n,V}) \|_{L_p(\mathcal{L} G)} \\ &\leq \|T_{\phi }\,:\, L_{p_1} \times \ldots \times L_{p_n} \to L_p\| \sum _{j=1}^n\left ( \|(T_{\zeta _j} - \iota _{p_j})(y_{j,V})\|_{L_{p_j}(\mathcal{L} G)} \prod _{i \neq j} \|y_{i,V}\|_{p_i}\right ). \end{split} \end{equation}
By (2.1), we have
![]() $\|y_{j,V}\|_{p_j} = 1$
. Further, by applying again Lemma 3.6 and Proposition 4.3,
$\|y_{j,V}\|_{p_j} = 1$
. Further, by applying again Lemma 3.6 and Proposition 4.3,
for
![]() $1 \leq j \leq i-1$
. Filling in the definition of
$1 \leq j \leq i-1$
. Filling in the definition of
![]() $\zeta _j$
,
$\zeta _j$
,
and this equals 0 when evaluated at
![]() $t_j, t_{j+1} = e$
. Similarly, we find for
$t_j, t_{j+1} = e$
. Similarly, we find for
![]() $i \leq j \leq n$
that
$i \leq j \leq n$
that
![]() $\lim _{V \in \mathcal{V}} \|(T_{\zeta _j} - \iota )(y_{j,V})\|_{L_{p_j}(\mathcal{L} G)}$
exists and equals 0 when evaluated at the identity in the corresponding
$\lim _{V \in \mathcal{V}} \|(T_{\zeta _j} - \iota )(y_{j,V})\|_{L_{p_j}(\mathcal{L} G)}$
exists and equals 0 when evaluated at the identity in the corresponding
![]() $t_1, \dots, t_n$
. Moreover, all these values are bounded by 2. Going back to (4.4), let us write
$t_1, \dots, t_n$
. Moreover, all these values are bounded by 2. Going back to (4.4), let us write
![]() $M\,:\!=\,\|T_{\phi }\,:\, L_{p_1} \times \ldots \times L_{p_n} \to L_p\|$
. We find
$M\,:\!=\,\|T_{\phi }\,:\, L_{p_1} \times \ldots \times L_{p_n} \to L_p\|$
. We find
 \begin{equation} \begin{split} C_{k,V} \leq & \int _{G^{\times n}} M \left (\sum _{j=1}^n \|(T_{\zeta _j} - \iota )(y_{j,V})\|_{L_{p_j}(\mathcal{L} G)} \right ) \left (\prod _{j=1}^n |\varphi _k(t_j)| \right ) dt_1 \ldots dt_n. \end{split} \end{equation}
\begin{equation} \begin{split} C_{k,V} \leq & \int _{G^{\times n}} M \left (\sum _{j=1}^n \|(T_{\zeta _j} - \iota )(y_{j,V})\|_{L_{p_j}(\mathcal{L} G)} \right ) \left (\prod _{j=1}^n |\varphi _k(t_j)| \right ) dt_1 \ldots dt_n. \end{split} \end{equation}
The integrand of (4.6) is bounded by the integrable function
![]() $2M\prod _{i=1}^n |\varphi _k(t_j)|$
. Hence, by Lebesgue’s dominated convergence theorem, the right-hand side of (4.6) converges in
$2M\prod _{i=1}^n |\varphi _k(t_j)|$
. Hence, by Lebesgue’s dominated convergence theorem, the right-hand side of (4.6) converges in
![]() $V$
. We find that
$V$
. We find that
 \begin{align*} \begin{split} &\limsup _{V \in \mathcal{V}} C_{k,V} \leq M \int _{G^{\times n}} \left ( \sum _{j=1}^n \lim _{V \in \mathcal{V}} \|(T_{\zeta _j} - \iota )(y_{j,V})\|_{L_{p_j}(\mathcal{L} G)} \right )\left (\prod _{i=1}^n |\varphi _k(t_j)|\right ) dt_1 \dots dt_n. \end{split} \end{align*}
\begin{align*} \begin{split} &\limsup _{V \in \mathcal{V}} C_{k,V} \leq M \int _{G^{\times n}} \left ( \sum _{j=1}^n \lim _{V \in \mathcal{V}} \|(T_{\zeta _j} - \iota )(y_{j,V})\|_{L_{p_j}(\mathcal{L} G)} \right )\left (\prod _{i=1}^n |\varphi _k(t_j)|\right ) dt_1 \dots dt_n. \end{split} \end{align*}
This quantity goes to 0 in
![]() $k$
. This concludes the proof for
$k$
. This concludes the proof for
![]() $C_{k,V}$
.
$C_{k,V}$
.
Finally, we prove that
![]() $\lim _{V \in \mathcal{V}} B_{k,V} = 0$
for any
$\lim _{V \in \mathcal{V}} B_{k,V} = 0$
for any
![]() $k$
. We fix a
$k$
. We fix a
![]() $k$
for the remainder of the proof. Recall that since
$k$
for the remainder of the proof. Recall that since
![]() $\varphi _k \in A(G)$
,
$\varphi _k \in A(G)$
,
![]() $T_{\varphi _k}$
is bounded on
$T_{\varphi _k}$
is bounded on
![]() $L_q(\mathcal{L} G)$
for any
$L_q(\mathcal{L} G)$
for any
![]() $1 \leq q \leq \infty$
. Moreover, since
$1 \leq q \leq \infty$
. Moreover, since
![]() $\varphi _k \in C_c(G) \star C_c(G)$
, we also have
$\varphi _k \in C_c(G) \star C_c(G)$
, we also have
![]() $\varphi _k \Delta \in C_c(G) \star C_c(G) \subseteq A(G)$
(cf. the calculation before (2.6)), hence
$\varphi _k \Delta \in C_c(G) \star C_c(G) \subseteq A(G)$
(cf. the calculation before (2.6)), hence
![]() $T_{\varphi _k \Delta }$
is also bounded on
$T_{\varphi _k \Delta }$
is also bounded on
![]() $L_q(\mathcal{L} G)$
for any
$L_q(\mathcal{L} G)$
for any
![]() $q$
.
$q$
.
We may assume, by scaling
![]() $\varphi _k$
if necessary, that
$\varphi _k$
if necessary, that
![]() $T_{\varphi _k}\,:\, L_q(\mathcal{L} G) \to L_q(\mathcal{L} G)$
and
$T_{\varphi _k}\,:\, L_q(\mathcal{L} G) \to L_q(\mathcal{L} G)$
and
![]() $T_{\varphi _k \Delta }\,:\, L_q(\mathcal{L} G) \to L_q(\mathcal{L} G)$
are contractions for any Hölder combination
$T_{\varphi _k \Delta }\,:\, L_q(\mathcal{L} G) \to L_q(\mathcal{L} G)$
are contractions for any Hölder combination
![]() $q$
of
$q$
of
![]() $p_1, \dots, p_n$
. Of course, this means that
$p_1, \dots, p_n$
. Of course, this means that
![]() $\|\varphi _k\|_1$
need no longer be
$\|\varphi _k\|_1$
need no longer be
![]() $1$
from now on. Set
$1$
from now on. Set
 \begin{align*} \begin{split} \psi _k(s_1, \dots, s_n; t_1, \dots, t_n) &\,:\!=\, \left ( \prod _{j=1}^i \varphi _k(r_{j-1} s_j\ldots s_{i} r_{i}^{-1} t_j)\right )\\ & \quad \times \left ( \prod _{j=i+1}^n \varphi _k(t_j r_{i} s_{i+1} \ldots s_j r_j^{-1}) \Delta (r_{i} s_{i+1} \ldots s_j r_j^{-1})\right ) \\ &\,=\!:\, \psi _k^1(s_1, \dots, s_i; t_1, \dots, t_i) \psi _k^2(s_{i+1}, \dots, s_n; t_{i+1}, \dots, t_n). \end{split} \end{align*}
\begin{align*} \begin{split} \psi _k(s_1, \dots, s_n; t_1, \dots, t_n) &\,:\!=\, \left ( \prod _{j=1}^i \varphi _k(r_{j-1} s_j\ldots s_{i} r_{i}^{-1} t_j)\right )\\ & \quad \times \left ( \prod _{j=i+1}^n \varphi _k(t_j r_{i} s_{i+1} \ldots s_j r_j^{-1}) \Delta (r_{i} s_{i+1} \ldots s_j r_j^{-1})\right ) \\ &\,=\!:\, \psi _k^1(s_1, \dots, s_i; t_1, \dots, t_i) \psi _k^2(s_{i+1}, \dots, s_n; t_{i+1}, \dots, t_n). \end{split} \end{align*}
By using the last term of (4.1) and Fubini, we get
 \begin{equation} \begin{split} B_{k,V} &\leq \int _{G^{\times n}} |(\phi (\zeta _1, \dots, \zeta _n))_{t_1, \dots, t_n}(e, \dots, e)| \\ & \qquad \times \| T_{\psi _k({\cdot}; t_1, \dots, t_n)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - \psi _k(1, \ldots, 1; t_1, \dots t_n) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} dt_1 \ldots dt_n.\\ \end{split} \end{equation}
\begin{equation} \begin{split} B_{k,V} &\leq \int _{G^{\times n}} |(\phi (\zeta _1, \dots, \zeta _n))_{t_1, \dots, t_n}(e, \dots, e)| \\ & \qquad \times \| T_{\psi _k({\cdot}; t_1, \dots, t_n)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - \psi _k(1, \ldots, 1; t_1, \dots t_n) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} dt_1 \ldots dt_n.\\ \end{split} \end{equation}
Note that
![]() $|\varphi _k| \leq 1$
by the assumed contractivity of
$|\varphi _k| \leq 1$
by the assumed contractivity of
![]() $T_{\varphi _k}$
. Indeed, for
$T_{\varphi _k}$
. Indeed, for
![]() $s \in G$
, apply
$s \in G$
, apply
![]() $T_{\varphi _k}$
to
$T_{\varphi _k}$
to
![]() $\lambda _s$
to deduce that
$\lambda _s$
to deduce that
![]() $|\varphi _k(s)| \leq 1$
. Hence,
$|\varphi _k(s)| \leq 1$
. Hence,
![]() $|\psi _k(1, \dots, 1; t_1, \dots, t_n)| \leq \prod _{j=i+1}^n \Delta (r_ir_j^{-1})$
. Moreover, from the expression (4.9) below, we see that
$|\psi _k(1, \dots, 1; t_1, \dots, t_n)| \leq \prod _{j=i+1}^n \Delta (r_ir_j^{-1})$
. Moreover, from the expression (4.9) below, we see that
![]() $\|T_{\psi _k({\cdot}; t_1, \dots, t_n)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}})\|_{L_p(\mathcal{L} G)} \leq \Delta ((t_{i+1}, \dots, t_n)^{-1})$
. Since
$\|T_{\psi _k({\cdot}; t_1, \dots, t_n)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}})\|_{L_p(\mathcal{L} G)} \leq \Delta ((t_{i+1}, \dots, t_n)^{-1})$
. Since
![]() $\phi (\zeta _1, \dots, \zeta _n)$
is compactly supported, the integrand of (4.7) is dominated by an integrable function. Hence by the Lebesgue dominated convergence theorem, it suffices to show that the term
$\phi (\zeta _1, \dots, \zeta _n)$
is compactly supported, the integrand of (4.7) is dominated by an integrable function. Hence by the Lebesgue dominated convergence theorem, it suffices to show that the term
goes to 0 in
![]() $V$
for any choice of
$V$
for any choice of
![]() $t_1, \dots, t_n \in G$
.
$t_1, \dots, t_n \in G$
.
Fix
![]() $t_1, \dots, t_n \in G$
. For
$t_1, \dots, t_n \in G$
. For
![]() $1 \leq j \leq i$
, set
$1 \leq j \leq i$
, set
![]() $q_j^{-1} = \sum _{l=j}^{i} p_l^{-1}$
(so
$q_j^{-1} = \sum _{l=j}^{i} p_l^{-1}$
(so
![]() $q_1 = \bar{p}_1$
) and
$q_1 = \bar{p}_1$
) and
![]() $T_j = T_{\varphi _k(r_{j-1} {\cdot} r_{i}^{-1} t_j)}$
. By Lemma 3.6,
$T_j = T_{\varphi _k(r_{j-1} {\cdot} r_{i}^{-1} t_j)}$
. By Lemma 3.6,
![]() $T_j$
is a contraction on
$T_j$
is a contraction on
![]() $L_{q_j}(\mathcal{L} G)$
. For
$L_{q_j}(\mathcal{L} G)$
. For
![]() $i+1 \leq j \leq n$
, set
$i+1 \leq j \leq n$
, set
![]() $q_j^{-1} = \sum _{l=j}^n p_l^{-1}$
(so
$q_j^{-1} = \sum _{l=j}^n p_l^{-1}$
(so
![]() $q_{i+1} = \bar{p}_2$
) and
$q_{i+1} = \bar{p}_2$
) and
![]() $T_j = T_{\varphi _k(t_j r_i{\cdot} r_j^{-1}) \Delta (r_i {\cdot} r_j^{-1})}$
. We can estimate the norm of
$T_j = T_{\varphi _k(t_j r_i{\cdot} r_j^{-1}) \Delta (r_i {\cdot} r_j^{-1})}$
. We can estimate the norm of
![]() $T_j: L_{q_j}(\mathcal{L} G) \to L_{q_j}(\mathcal{L} G)$
by using again Lemma 3.6:
$T_j: L_{q_j}(\mathcal{L} G) \to L_{q_j}(\mathcal{L} G)$
by using again Lemma 3.6:
Now, by Lemma 3.8, we have
 \begin{align*} \begin{split} T_{\psi _k^1(\cdot ; t_1, \dots, t_i)}(h_V^{\frac 2{p_1}}, \dots, h_V^{\frac 2{p_i}}) &= T_1(h_V^{\frac 2{p_1}} T_2(h_V^{\frac 2{p_2}} \dots T_i(h_V^{\frac 2{p_i}}) \dots )), \\ T_{\psi _k^2(\cdot ; t_{i+1}, \dots, t_n)}(h_V^{\frac 2{p_{i+1}}}, \dots, h_V^{\frac 2{p_n}}) &= T_{i+1}(h_V^{\frac 2{p_{i+1}}} T_{i+2}(h_V^{\frac 2{p_{i+2}}} \dots T_n(h_V^{\frac 2{p_n}}) \dots )). \end{split} \end{align*}
\begin{align*} \begin{split} T_{\psi _k^1(\cdot ; t_1, \dots, t_i)}(h_V^{\frac 2{p_1}}, \dots, h_V^{\frac 2{p_i}}) &= T_1(h_V^{\frac 2{p_1}} T_2(h_V^{\frac 2{p_2}} \dots T_i(h_V^{\frac 2{p_i}}) \dots )), \\ T_{\psi _k^2(\cdot ; t_{i+1}, \dots, t_n)}(h_V^{\frac 2{p_{i+1}}}, \dots, h_V^{\frac 2{p_n}}) &= T_{i+1}(h_V^{\frac 2{p_{i+1}}} T_{i+2}(h_V^{\frac 2{p_{i+2}}} \dots T_n(h_V^{\frac 2{p_n}}) \dots )). \end{split} \end{align*}
Clearly,
![]() $T_{\psi _k^1(\cdot ; t_1, \dots, t_i)}$
is contractive as a map on
$T_{\psi _k^1(\cdot ; t_1, \dots, t_i)}$
is contractive as a map on
![]() $L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_i}(\mathcal{L} G)$
. Let
$L_{p_1}(\mathcal{L} G) \times \ldots \times L_{p_i}(\mathcal{L} G)$
. Let
![]() $x_j \in L_{p_j}(\mathcal{L} G)$
with
$x_j \in L_{p_j}(\mathcal{L} G)$
with
![]() $\|x_j\|_{L_{p_j}(\mathcal{L} G)} \leq 1$
; then, from (3.4),
$\|x_j\|_{L_{p_j}(\mathcal{L} G)} \leq 1$
; then, from (3.4),
This validates the use of the dominated convergence theorem above. Now we go back to estimating (4.8). Using subsequently the triangle inequality and Hölder’s inequality (with again [3.4]), we find
 \begin{align*} \begin{split} &\| T_{\psi _k({\cdot}; t_1, \dots, t_n)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - \psi _k(1, \ldots, 1; t_1, \dots t_n) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\quad\leq \|T_{\psi ^1_k({\cdot}; t_1, \dots, t_i)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_i}}) \cdot \psi _k^2(1, \dots, 1; t_{i+1}, \dots, t_n) h_V^{\frac 2{\bar{p}_2}} - \psi _k(1, \ldots, 1; t_1, \dots t_n) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\qquad + \| T_{\psi _k({\cdot}; t_1, \dots, t_n)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - T_{\psi ^1_k({\cdot}; t_1, \dots, t_i)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_i}}) \cdot \psi _k^2(1, \dots, 1; t_{i+1}, \dots, t_n) h_V^{\frac 2{\bar{p}_2}}\|_{L_p(\mathcal{L} G)}\\ &\quad\leq \left (\prod _{j=i+1}^n \Delta (r_ir_j^{-1})\right ) \|T_{\psi ^1_k({\cdot}; t_1, \dots, t_i)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_i}}) - \psi _k^1(1, \dots, 1; t_1, \dots, t_i) h_V^{\frac 2{\bar{p}_1}}\|_{L_{\bar{p}_1}(\mathcal{L} G)} \\ &\qquad + \|T_{\psi _k^2(\cdot ; t_{i+1}, \dots, t_n)}(h_V^{\frac 2{p_{i+1}}}, \dots, h_V^{\frac 2{p_n}}) - \psi _k^2(1, \dots, 1; t_{i+1}, \dots, t_n) h_V^{\frac 2{\bar{p}_2}} \|_{L_{\bar{p}_2}(\mathcal{L} G)} \\ &\quad \,=\!:\, B_{k,V}^1 + B_{k,V}^2. \end{split} \end{align*}
\begin{align*} \begin{split} &\| T_{\psi _k({\cdot}; t_1, \dots, t_n)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - \psi _k(1, \ldots, 1; t_1, \dots t_n) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\quad\leq \|T_{\psi ^1_k({\cdot}; t_1, \dots, t_i)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_i}}) \cdot \psi _k^2(1, \dots, 1; t_{i+1}, \dots, t_n) h_V^{\frac 2{\bar{p}_2}} - \psi _k(1, \ldots, 1; t_1, \dots t_n) h_V^{\frac 2p} \|_{L_p(\mathcal{L} G)} \\ &\qquad + \| T_{\psi _k({\cdot}; t_1, \dots, t_n)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_n}}) - T_{\psi ^1_k({\cdot}; t_1, \dots, t_i)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_i}}) \cdot \psi _k^2(1, \dots, 1; t_{i+1}, \dots, t_n) h_V^{\frac 2{\bar{p}_2}}\|_{L_p(\mathcal{L} G)}\\ &\quad\leq \left (\prod _{j=i+1}^n \Delta (r_ir_j^{-1})\right ) \|T_{\psi ^1_k({\cdot}; t_1, \dots, t_i)}(h_V^{\frac 2{p_1}}, \ldots, h_V^{\frac 2{p_i}}) - \psi _k^1(1, \dots, 1; t_1, \dots, t_i) h_V^{\frac 2{\bar{p}_1}}\|_{L_{\bar{p}_1}(\mathcal{L} G)} \\ &\qquad + \|T_{\psi _k^2(\cdot ; t_{i+1}, \dots, t_n)}(h_V^{\frac 2{p_{i+1}}}, \dots, h_V^{\frac 2{p_n}}) - \psi _k^2(1, \dots, 1; t_{i+1}, \dots, t_n) h_V^{\frac 2{\bar{p}_2}} \|_{L_{\bar{p}_2}(\mathcal{L} G)} \\ &\quad \,=\!:\, B_{k,V}^1 + B_{k,V}^2. \end{split} \end{align*}
We show only that
![]() $\lim _{V \in \mathcal{V}} B_{k,V}^2 = 0$
; the equality
$\lim _{V \in \mathcal{V}} B_{k,V}^2 = 0$
; the equality
![]() $\lim _{V \in \mathcal{V}} B_{k,V}^1 = 0$
follows similarly and is in fact slightly easier since the
$\lim _{V \in \mathcal{V}} B_{k,V}^1 = 0$
follows similarly and is in fact slightly easier since the
![]() $T_j$
are contractions for
$T_j$
are contractions for
![]() $j \leq i$
. Now set, for
$j \leq i$
. Now set, for
![]() $i \leq j \leq n$
,
$i \leq j \leq n$
,
 \begin{equation*} R_{j,V} \,:\!=\, \left (\prod _{l=j+1}^{n} \varphi _k(t_l r_i r_l^{-1}) \right ) T_{i+1}(h_V^{\frac 2{p_{i+1}}} \ldots T_j( h_V^{\frac 2{q_j}}) \ldots ). \end{equation*}
\begin{equation*} R_{j,V} \,:\!=\, \left (\prod _{l=j+1}^{n} \varphi _k(t_l r_i r_l^{-1}) \right ) T_{i+1}(h_V^{\frac 2{p_{i+1}}} \ldots T_j( h_V^{\frac 2{q_j}}) \ldots ). \end{equation*}
Here
![]() $R_{i,V} = \prod _{l=i+1}^{n-1} \varphi _k(t_l r_i r_l^{-1}) h_V^{\frac 2{q_1}}$
. Then
$R_{i,V} = \prod _{l=i+1}^{n-1} \varphi _k(t_l r_i r_l^{-1}) h_V^{\frac 2{q_1}}$
. Then
Recall that
![]() $|\varphi _k| \leq 1$
. Hence
$|\varphi _k| \leq 1$
. Hence
 \begin{align*} \begin{split} &\|R_{j,V} - R_{j-1,V}\|_{L_{\bar{p}_2}(\mathcal{L} G)} \\ &\quad= \left (\prod _{l=j+1}^n |\varphi _k(t_l r_i r_l^{-1})|\right ) \|T_{i+1}(h_V^{\frac 2{p_{i+1}}} \ldots T_{j-1}(h_V^{\frac 2{p_{j-1}}}(T_j(h_V^{\frac 2{q_j}}) - \varphi _k(t_j r_i r_j^{-1}) h_V^{\frac 2{q_j}})) \ldots )\|_{L_{\bar{p}_2}(\mathcal{L} G)} \\ &\quad\leq \Delta ((t_{i+1} \ldots t_n)^{-1}) \|T_j(h_V^{\frac 2{q_j}}) - \varphi _k(t_j r_i r_j^{-1}) h_V^{\frac 2{q_j}}\|_{L_{q_j}(\mathcal{L} G)}. \end{split} \end{align*}
\begin{align*} \begin{split} &\|R_{j,V} - R_{j-1,V}\|_{L_{\bar{p}_2}(\mathcal{L} G)} \\ &\quad= \left (\prod _{l=j+1}^n |\varphi _k(t_l r_i r_l^{-1})|\right ) \|T_{i+1}(h_V^{\frac 2{p_{i+1}}} \ldots T_{j-1}(h_V^{\frac 2{p_{j-1}}}(T_j(h_V^{\frac 2{q_j}}) - \varphi _k(t_j r_i r_j^{-1}) h_V^{\frac 2{q_j}})) \ldots )\|_{L_{\bar{p}_2}(\mathcal{L} G)} \\ &\quad\leq \Delta ((t_{i+1} \ldots t_n)^{-1}) \|T_j(h_V^{\frac 2{q_j}}) - \varphi _k(t_j r_i r_j^{-1}) h_V^{\frac 2{q_j}}\|_{L_{q_j}(\mathcal{L} G)}. \end{split} \end{align*}
We know that
![]() $q_j \gt \bar{p}_2 \gt 1$
for any
$q_j \gt \bar{p}_2 \gt 1$
for any
![]() $i+1 \leq j \leq n$
. Additionally,
$i+1 \leq j \leq n$
. Additionally,
![]() $T_j$
is bounded on
$T_j$
is bounded on
![]() $\mathcal{L} G$
and
$\mathcal{L} G$
and
![]() $L_1(\mathcal{L} G)$
. By Proposition 4.3, the above terms converge to 0 in
$L_1(\mathcal{L} G)$
. By Proposition 4.3, the above terms converge to 0 in
![]() $V$
. Hence,
$V$
. Hence,
![]() $\lim _{V \in \mathcal{V}} B_{k,V}^2 = 0$
. This finishes the proof.
$\lim _{V \in \mathcal{V}} B_{k,V}^2 = 0$
. This finishes the proof.
Remark 4.4.
As in the unimodular case (see [Reference Caspers, Krishnaswamy-Usha and Vos6
, Remark 3.3]) we do not know if Theorem
4.1
holds if
![]() $p = p_i = 1$
for some
$p = p_i = 1$
for some
![]() $1 \leq i \leq n$
(and
$1 \leq i \leq n$
(and
![]() $p_j = \infty$
for all
$p_j = \infty$
for all
![]() $j \neq i$
). The proof above fails in that case because we cannot apply Proposition 4.3.
$j \neq i$
). The proof above fails in that case because we cannot apply Proposition 4.3.
5. Schur to Fourier transference for amenable groups
In this section, we extend [Reference Caspers, Krishnaswamy-Usha and Vos6, Proof of Theorem 4.1], that is, the transference from Schur multipliers to Fourier multipliers for amenable groups, to the non-unimodular setting. The proof is essentially the same but with extra technicalities due to the modular function. We also fixed a small mistake in the proof, as will be mentioned at the relevant spot.
Recall [Reference Paterson19, Theorem 4.10] that
![]() $G$
is amenable iff it satisfies the following Følner condition: for any
$G$
is amenable iff it satisfies the following Følner condition: for any
![]() $\varepsilon \gt 0$
and any compact set
$\varepsilon \gt 0$
and any compact set
![]() $K\subseteq G$
, there exists a compact set
$K\subseteq G$
, there exists a compact set
![]() $F \subseteq G$
with nonzero measure such that
$F \subseteq G$
with nonzero measure such that
![]() $\frac{\mu ((sF \setminus F) \cup (F \setminus sF))}{\mu (F)} \lt \varepsilon$
for all
$\frac{\mu ((sF \setminus F) \cup (F \setminus sF))}{\mu (F)} \lt \varepsilon$
for all
![]() $s\in K$
. This allows us to construct a net
$s\in K$
. This allows us to construct a net
![]() $F_{(\varepsilon, K)}$
of such Følner sets using the ordering
$F_{(\varepsilon, K)}$
of such Følner sets using the ordering
![]() $( \varepsilon _1, K_1) \leq (\varepsilon _2,K_2)$
if
$( \varepsilon _1, K_1) \leq (\varepsilon _2,K_2)$
if
![]() $\varepsilon _1 \geq \varepsilon _2, K_1 \subseteq K_2$
.
$\varepsilon _1 \geq \varepsilon _2, K_1 \subseteq K_2$
.
Theorem 5.1.
Let
![]() $G$
be a locally compact, amenable group and let
$G$
be a locally compact, amenable group and let
![]() $1\leq p,p^{\prime},p_1,\ldots, p_n \leq \infty$
be such that
$1\leq p,p^{\prime},p_1,\ldots, p_n \leq \infty$
be such that
![]() $\frac 1p=\sum _{i=1}^n \frac 1{p_i} = 1 - \frac 1{p^{\prime}}$
. Let
$\frac 1p=\sum _{i=1}^n \frac 1{p_i} = 1 - \frac 1{p^{\prime}}$
. Let
![]() $\phi \in L_\infty (G^{\times n})$
and define
$\phi \in L_\infty (G^{\times n})$
and define
![]() $\widetilde{\phi } \in L_\infty (G^{\times n + 1})$
by
$\widetilde{\phi } \in L_\infty (G^{\times n + 1})$
by
Assume that
![]() $\widetilde{\phi }$
defines a
$\widetilde{\phi }$
defines a
![]() $(p_1,\ldots, p_n)$
-Schur multiplier of
$(p_1,\ldots, p_n)$
-Schur multiplier of
![]() $G$
. Then there is a net
$G$
. Then there is a net
![]() $I$
, and there are complete contractions
$I$
, and there are complete contractions
![]() $i_{q,\alpha }\,:\, L_q(\mathcal{L} G) \to S_q(L_2(G))$
,
$i_{q,\alpha }\,:\, L_q(\mathcal{L} G) \to S_q(L_2(G))$
,
![]() $\alpha \in I$
, such that for all
$\alpha \in I$
, such that for all
![]() $f_i,f \in C_c(G)\star C_c(G)$
,
$f_i,f \in C_c(G)\star C_c(G)$
,
where
![]() $x_i = \Delta ^{a_i}\lambda (f_i)\Delta ^{b_i} \in L^{p_i}(\mathcal{L} G),\ y = \Delta ^a \lambda (f) \Delta ^b \in L^{p^{\prime}}(\mathcal{L} G)$
(i.e.
$x_i = \Delta ^{a_i}\lambda (f_i)\Delta ^{b_i} \in L^{p_i}(\mathcal{L} G),\ y = \Delta ^a \lambda (f) \Delta ^b \in L^{p^{\prime}}(\mathcal{L} G)$
(i.e.
![]() $a_i + b_i = \frac 1{p_i}$
). In a similar way, the matrix amplifications of
$a_i + b_i = \frac 1{p_i}$
). In a similar way, the matrix amplifications of
![]() $i_{q,\alpha }$
approximately intertwine the multiplicative amplifications of the Fourier and Schur multipliers.
$i_{q,\alpha }$
approximately intertwine the multiplicative amplifications of the Fourier and Schur multipliers.
Proof. Let
![]() $F_\alpha, \alpha \in I$
be a Følner net for
$F_\alpha, \alpha \in I$
be a Følner net for
![]() $G$
, where
$G$
, where
![]() $I$
is the index set consisting of pairs
$I$
is the index set consisting of pairs
![]() $(\varepsilon, K)$
for
$(\varepsilon, K)$
for
![]() $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,
![]() $K \subseteq G$
compact and the ordering as described above.
$K \subseteq G$
compact and the ordering as described above.
Let
![]() $P_\alpha =P_{F_\alpha }$
be the projection of
$P_\alpha =P_{F_\alpha }$
be the projection of
![]() $L_2(G)$
onto
$L_2(G)$
onto
![]() $L_2(F_\alpha )$
. Consider the maps
$L_2(F_\alpha )$
. Consider the maps
![]() $i_{p,\alpha }\,:\, L_p(\mathcal{L} G)\to S_p(L_2(G))$
defined by
$i_{p,\alpha }\,:\, L_p(\mathcal{L} G)\to S_p(L_2(G))$
defined by
![]() $i_{p,\alpha }(x) = \mu (F_\alpha )^{-1/p} P_{\alpha }x P_{\alpha }$
. They are contractions by [Reference Caspers and de la Salle3, Theorem5.1]. By replacing
$i_{p,\alpha }(x) = \mu (F_\alpha )^{-1/p} P_{\alpha }x P_{\alpha }$
. They are contractions by [Reference Caspers and de la Salle3, Theorem5.1]. By replacing
![]() $G$
by
$G$
by
![]() $G \times SU(2)$
, one proves that they are in fact complete contractions (see also the last paragraph of [Reference Caspers and de la Salle3, Proof of Theorem 5.2]).
$G \times SU(2)$
, one proves that they are in fact complete contractions (see also the last paragraph of [Reference Caspers and de la Salle3, Proof of Theorem 5.2]).
Now fix
![]() $\alpha$
. From (2.10), we deduce
$\alpha$
. From (2.10), we deduce
 \begin{align*} M_{\widetilde{\phi }} (i_{p_1, \alpha }(x_1),\ldots, i_{p_n, \alpha }(x_n)) (t_0,t_{n}) \\ = \frac{1}{\mu (F_\alpha )^{1/p}} 1_{F_\alpha }(t_0)1_{F_\alpha }(t_n) \int _{F_\alpha ^{\times n-1}} &\phi (t_0t_1^{-1},\ldots, t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) \times \\ & \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \ldots \Delta ^{b_n}(t_n) \Delta ((t_1 \ldots t_n)^{-1}) dt_1 \ldots dt_{n-1}. \end{align*}
\begin{align*} M_{\widetilde{\phi }} (i_{p_1, \alpha }(x_1),\ldots, i_{p_n, \alpha }(x_n)) (t_0,t_{n}) \\ = \frac{1}{\mu (F_\alpha )^{1/p}} 1_{F_\alpha }(t_0)1_{F_\alpha }(t_n) \int _{F_\alpha ^{\times n-1}} &\phi (t_0t_1^{-1},\ldots, t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) \times \\ & \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \ldots \Delta ^{b_n}(t_n) \Delta ((t_1 \ldots t_n)^{-1}) dt_1 \ldots dt_{n-1}. \end{align*}
From Lemma 3.9, we have a similar expression for the kernel of
![]() $i_{p,\alpha }(T_\phi (x_1, \dots, x_n))$
:
$i_{p,\alpha }(T_\phi (x_1, \dots, x_n))$
:
 \begin{align*} \begin{split} (t_0,t_n) \mapsto \frac 1{\mu (F_{\alpha })^{1/p}} 1_{F_{\alpha }}(t_0) 1_{F_{\alpha }}(t_n) & \int _{G^{\times n-1}} \phi (t_0t_1^{-1},\ldots, t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) \times \\ & \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \ldots \Delta ^{b_n}(t_n) \Delta ((t_1 \ldots t_n)^{-1}) dt_1\ldots dt_{n-1}. \end{split} \end{align*}
\begin{align*} \begin{split} (t_0,t_n) \mapsto \frac 1{\mu (F_{\alpha })^{1/p}} 1_{F_{\alpha }}(t_0) 1_{F_{\alpha }}(t_n) & \int _{G^{\times n-1}} \phi (t_0t_1^{-1},\ldots, t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) \times \\ & \Delta ^{a_1}(t_0) \Delta ^{b_1 + a_2}(t_1) \ldots \Delta ^{b_n}(t_n) \Delta ((t_1 \ldots t_n)^{-1}) dt_1\ldots dt_{n-1}. \end{split} \end{align*}
Now we need to take the pairing of these kernels with
![]() $i_{p^{\prime},\alpha }(y)$
and calculate their difference. To that end, we define the following function
$i_{p^{\prime},\alpha }(y)$
and calculate their difference. To that end, we define the following function
![]() $\Phi$
:
$\Phi$
:
and the function
![]() $\Psi _{\alpha }$
:
$\Psi _{\alpha }$
:
Note that in [Reference Caspers, Krishnaswamy-Usha and Vos6], the indicator function was mistakenly taken over
![]() $F_\alpha \times (F_\alpha ^c)^{\times n-1} \times F_{\alpha }$
instead. This correction leads to an extra term
$F_\alpha \times (F_\alpha ^c)^{\times n-1} \times F_{\alpha }$
instead. This correction leads to an extra term
![]() $n$
in the choice of the lower bound of
$n$
in the choice of the lower bound of
![]() $\alpha$
at the end. Also note that a priori, it is not clear that
$\alpha$
at the end. Also note that a priori, it is not clear that
![]() $T_\phi (x_1, \dots, x_n)$
lies in
$T_\phi (x_1, \dots, x_n)$
lies in
![]() $L_p(\mathcal{L} G)$
, and hence it is not clear that
$L_p(\mathcal{L} G)$
, and hence it is not clear that
![]() $i_{p,\alpha }(T_\phi (x_1, \dots, x_n))$
lies in
$i_{p,\alpha }(T_\phi (x_1, \dots, x_n))$
lies in
![]() $S_p(L_2(G))$
. However, both
$S_p(L_2(G))$
. However, both
![]() $i_{p,\alpha }(T_\phi (x_1, \dots, x_n))$
and
$i_{p,\alpha }(T_\phi (x_1, \dots, x_n))$
and
![]() $i_{p^{\prime},\alpha }(y)$
are given by integration against a kernel in
$i_{p^{\prime},\alpha }(y)$
are given by integration against a kernel in
![]() $L_2(G \times G)$
, so the pairing (2.9) is still well-defined as a pairing in
$L_2(G \times G)$
, so the pairing (2.9) is still well-defined as a pairing in
![]() $S_2(L_2(G))$
instead. Now we have
$S_2(L_2(G))$
instead. Now we have
 \begin{equation} \begin{split} &\vert \langle i_{p,\alpha }(T_\phi (x_1,\ldots, x_n)),i_{p^{\prime},\alpha }(y) \rangle - \langle M_{\widetilde{\phi }}( i_{p_1,\alpha }(x_1),\ldots, i_{p_n,\alpha }(x_n) ), i_{p^{\prime},\alpha }(y) \rangle \vert \\ &\quad= \left \vert \frac{1}{\mu (F_\alpha )} \int _{G^{\times n+1}} \Phi (t_0,\ldots, t_n) \Psi _\alpha (t_0,\ldots, t_n) dt_0 \ldots dt_n \right \vert \\ \end{split} \end{equation}
\begin{equation} \begin{split} &\vert \langle i_{p,\alpha }(T_\phi (x_1,\ldots, x_n)),i_{p^{\prime},\alpha }(y) \rangle - \langle M_{\widetilde{\phi }}( i_{p_1,\alpha }(x_1),\ldots, i_{p_n,\alpha }(x_n) ), i_{p^{\prime},\alpha }(y) \rangle \vert \\ &\quad= \left \vert \frac{1}{\mu (F_\alpha )} \int _{G^{\times n+1}} \Phi (t_0,\ldots, t_n) \Psi _\alpha (t_0,\ldots, t_n) dt_0 \ldots dt_n \right \vert \\ \end{split} \end{equation}
Let
![]() $K \subseteq G$
be some compact set such that
$K \subseteq G$
be some compact set such that
![]() $\mathrm{supp}(f_j),\mathrm{supp}(f)\subseteq K$
and
$\mathrm{supp}(f_j),\mathrm{supp}(f)\subseteq K$
and
![]() $e \in K$
. Let
$e \in K$
. Let
![]() $t_0, \dots, t_n$
be such that both
$t_0, \dots, t_n$
be such that both
![]() $\Phi (t_0, \dots, t_n)$
and
$\Phi (t_0, \dots, t_n)$
and
![]() $\Psi _\alpha (t_0, \dots, t_n)$
are nonzero. Since
$\Psi _\alpha (t_0, \dots, t_n)$
are nonzero. Since
![]() $\Psi _\alpha (t_0, \dots, t_n)$
is nonzero, we must have
$\Psi _\alpha (t_0, \dots, t_n)$
is nonzero, we must have
![]() $t_0, t_n \in F_\alpha$
and
$t_0, t_n \in F_\alpha$
and
![]() $t_i \notin F_\alpha$
for some
$t_i \notin F_\alpha$
for some
![]() $i \in \{1, \dots, n-1\}$
. Since
$i \in \{1, \dots, n-1\}$
. Since
![]() $\Phi (t_0, \dots, t_n)$
is nonzero, there are
$\Phi (t_0, \dots, t_n)$
is nonzero, there are
![]() $k_1,\ldots, k_n \in K$
such that
$k_1,\ldots, k_n \in K$
such that
![]() $t_{n-1} = k_n t_n,\ t_{n-2} = k_{n-1}k_n t_n,\ \ldots, \ t_0 = k_1 \ldots k_n t_n$
. Hence we find
$t_{n-1} = k_n t_n,\ t_{n-2} = k_{n-1}k_n t_n,\ \ldots, \ t_0 = k_1 \ldots k_n t_n$
. Hence we find
 \begin{equation} \begin{split} t_n &\in F_\alpha \cap (k_1\ldots k_n)^{-1}F_\alpha \setminus \left ( (k_2\ldots k_n)^{-1}F_\alpha \cap \ldots \cap k_n^{-1}F_\alpha \right ) \\ &\subseteq F_\alpha \setminus \left ( (k_2\ldots k_n)^{-1}F_\alpha \cap \ldots \cap k_n^{-1}F_\alpha \right ) \\ &= (F_\alpha \setminus (k_2\ldots k_n)^{-1}F_\alpha ) \cup \ldots \cup (F_\alpha \setminus k_n^{-1} F_\alpha ) \end{split} \end{equation}
\begin{equation} \begin{split} t_n &\in F_\alpha \cap (k_1\ldots k_n)^{-1}F_\alpha \setminus \left ( (k_2\ldots k_n)^{-1}F_\alpha \cap \ldots \cap k_n^{-1}F_\alpha \right ) \\ &\subseteq F_\alpha \setminus \left ( (k_2\ldots k_n)^{-1}F_\alpha \cap \ldots \cap k_n^{-1}F_\alpha \right ) \\ &= (F_\alpha \setminus (k_2\ldots k_n)^{-1}F_\alpha ) \cup \ldots \cup (F_\alpha \setminus k_n^{-1} F_\alpha ) \end{split} \end{equation}
We want to apply a change of variables in (5.2). Let us first look at a simple case: assume
![]() $g \in L_1(G \times G)$
is such that
$g \in L_1(G \times G)$
is such that
![]() $g(s,t) \neq 0$
only when
$g(s,t) \neq 0$
only when
![]() $st^{-1} \in K$
. Then
$st^{-1} \in K$
. Then
 \begin{align*} \begin{split} \int _{G^{\times 2}} g(s,t) ds dt &= \int _{G^{\times 2}} 1_K(s t^{-1}) g(s, t) ds dt = \int _{G^{\times 2}} 1_K(s) g(s t, t) \Delta (t) ds dt \\ &= \int _G \int _K g(k_1 t, t) \Delta (t) dk_1 dt \end{split} \end{align*}
\begin{align*} \begin{split} \int _{G^{\times 2}} g(s,t) ds dt &= \int _{G^{\times 2}} 1_K(s t^{-1}) g(s, t) ds dt = \int _{G^{\times 2}} 1_K(s) g(s t, t) \Delta (t) ds dt \\ &= \int _G \int _K g(k_1 t, t) \Delta (t) dk_1 dt \end{split} \end{align*}
where we renamed the variable
![]() $s$
in the last line. Applying the above formula twice for a function
$s$
in the last line. Applying the above formula twice for a function
![]() $g \in L_1(G^{\times 3})$
such that
$g \in L_1(G^{\times 3})$
such that
![]() $g(r,s,t) \neq 0$
only when
$g(r,s,t) \neq 0$
only when
![]() $rs^{-1} \in K$
,
$rs^{-1} \in K$
,
![]() $st^{-1} \in K$
, we get
$st^{-1} \in K$
, we get
 \begin{align*} \begin{split} \int _{G^{\times 3}} g(r,s,t) dr ds dt &= \int _{G^{\times 2}} \int _K g(k_1 s, s, t) \Delta (s) dk_1 ds dt \\ &= \int _G \int _{K^{\times 2}} g(k_1k_2 t, k_2t, t) \Delta (k_2t) \Delta (t) dk_1 dk_2 dt. \end{split} \end{align*}
\begin{align*} \begin{split} \int _{G^{\times 3}} g(r,s,t) dr ds dt &= \int _{G^{\times 2}} \int _K g(k_1 s, s, t) \Delta (s) dk_1 ds dt \\ &= \int _G \int _{K^{\times 2}} g(k_1k_2 t, k_2t, t) \Delta (k_2t) \Delta (t) dk_1 dk_2 dt. \end{split} \end{align*}
Carrying on like this, we obtain
 \begin{equation} \begin{split} &\left \vert \frac{1}{\mu (F_\alpha )} \int _{G^{\times n+1}} \Phi (t_0,\ldots, t_n) \Psi _\alpha (t_0,\ldots, t_n) dt_0 \ldots dt_n \right \vert \\ &\quad= \bigg \vert \frac{1}{\mu (F_\alpha )} \int _{K^{\times n}} \int _{G} \Phi (k_1\ldots k_n t_n, \ldots, k_n t_n, t_n) \Psi _\alpha (k_1\ldots k_nt_n,\ldots, k_nt_n, t_n) \times \\ & \qquad \Delta (k_2 \dots k_n t_n) \dots \Delta (k_nt_n) \Delta (t_n) dt_n dk_1 \ldots dk_n \bigg \vert . \\ \end{split} \end{equation}
\begin{equation} \begin{split} &\left \vert \frac{1}{\mu (F_\alpha )} \int _{G^{\times n+1}} \Phi (t_0,\ldots, t_n) \Psi _\alpha (t_0,\ldots, t_n) dt_0 \ldots dt_n \right \vert \\ &\quad= \bigg \vert \frac{1}{\mu (F_\alpha )} \int _{K^{\times n}} \int _{G} \Phi (k_1\ldots k_n t_n, \ldots, k_n t_n, t_n) \Psi _\alpha (k_1\ldots k_nt_n,\ldots, k_nt_n, t_n) \times \\ & \qquad \Delta (k_2 \dots k_n t_n) \dots \Delta (k_nt_n) \Delta (t_n) dt_n dk_1 \ldots dk_n \bigg \vert . \\ \end{split} \end{equation}
Note that
![]() $a + b + \sum _{i=1}^n a_i + b_i = 1$
, hence
$a + b + \sum _{i=1}^n a_i + b_i = 1$
, hence
 \begin{equation} \begin{split} &|\Phi (k_1\ldots k_n t_n, \ldots, k_n t_n, t_n)|\Delta (k_2 \dots k_n t_n) \dots \Delta (k_nt_n) \Delta (t_n) \\ &\quad\leq \|\phi f_1 \dots f_n f\|_{\infty } \Delta ^{a_1+b}(k_1\ldots k_n t_n) \Delta ^{b_1+a_2+1}(k_2 \ldots k_n t_n) \ldots \Delta ^{b_{n-1} + a_n+1}(k_nt_n) \times \\ & \qquad \Delta ^{b_n + a+1}(t_n)\Delta (k_1^{-1} k_2^{-2} \dots k_n^{-n} t_n^{-n-1}) \\ &\quad= \|\phi f_1 \dots f_n f\|_{\infty } \Delta ^{a_1+b-1}(k_1) \Delta ^{a_1+a_2+b_1+b-1}(k_2) \ldots \Delta ^{1-b_n-a-1}(k_n) \\ &\quad\leq \|\phi f_1 \dots f_n f\|_{\infty } C_{K,n} \,=\!:\, M. \end{split} \end{equation}
\begin{equation} \begin{split} &|\Phi (k_1\ldots k_n t_n, \ldots, k_n t_n, t_n)|\Delta (k_2 \dots k_n t_n) \dots \Delta (k_nt_n) \Delta (t_n) \\ &\quad\leq \|\phi f_1 \dots f_n f\|_{\infty } \Delta ^{a_1+b}(k_1\ldots k_n t_n) \Delta ^{b_1+a_2+1}(k_2 \ldots k_n t_n) \ldots \Delta ^{b_{n-1} + a_n+1}(k_nt_n) \times \\ & \qquad \Delta ^{b_n + a+1}(t_n)\Delta (k_1^{-1} k_2^{-2} \dots k_n^{-n} t_n^{-n-1}) \\ &\quad= \|\phi f_1 \dots f_n f\|_{\infty } \Delta ^{a_1+b-1}(k_1) \Delta ^{a_1+a_2+b_1+b-1}(k_2) \ldots \Delta ^{1-b_n-a-1}(k_n) \\ &\quad\leq \|\phi f_1 \dots f_n f\|_{\infty } C_{K,n} \,=\!:\, M. \end{split} \end{equation}
Here the constant
![]() $C_{K,n}$
can be chosen to be dependent only on
$C_{K,n}$
can be chosen to be dependent only on
![]() $K$
and
$K$
and
![]() $n$
(and
$n$
(and
![]() $G$
).
$G$
).
Applying (5.2), (5.4), (5.5) and (5.3) consecutively, we get
 \begin{equation} \begin{split} &\vert \langle i_{p,\alpha }(T_\phi (x_1,\ldots, x_n)),i_{p^{\prime},\alpha }(y) \rangle _{p,p^{\prime}} - \langle M_{\widetilde{\phi }}( i_{p_1,\alpha }(x_1),\ldots, i_{p_n,\alpha }(x_n) ), i_{p^{\prime},\alpha }(y) \rangle \vert \\ &\quad= \bigg \vert \frac{1}{\mu (F_\alpha )} \int _{K^{\times n}} \int _{G} \Phi (k_1\ldots k_n t_n, \ldots, k_n t_n, t_n) \Psi _\alpha (k_1\ldots k_nt_n,\ldots, k_nt_n, t_n) \times \\ & \qquad \Delta (k_2 \dots k_n t_n) \dots \Delta (k_nt_n) \Delta (t_n) dt_n dk_1 \ldots dk_n \bigg \vert \\ &\quad\leq \frac{M}{\mu (F_\alpha )} \int _{K^{\times n}} \int _G \Psi _\alpha (k_1\ldots k_nt_n,\ldots, k_nt_n, t_n) dt_n dk_1 \ldots dk_n \\ &\quad= \frac{M}{\mu (F_\alpha )} \int _{K^{\times n}} \mu \left (F_\alpha \cap (k_1\ldots k_n)^{-1}F_\alpha \setminus \left ( (k_2\ldots k_n)^{-1}F_\alpha \cap \ldots \cap k_n^{-1}F_\alpha \right )\right ) dk_1 \ldots dk_n\\ &\quad\leq \frac{M}{\mu (F_\alpha )} \int _{K^{\times n}} \sum _{i=2}^n \mu (F_\alpha \setminus (k_i \ldots k_n)^{-1}F_\alpha ) dk_1 \ldots dk_n\\ & \quad\leq M (n-1) \mu (K)^n \sup _{k \in K^{1-n}} \frac{\mu (F_{\alpha } \setminus kF_{\alpha })}{\mu (F_\alpha )}. \end{split} \end{equation}
\begin{equation} \begin{split} &\vert \langle i_{p,\alpha }(T_\phi (x_1,\ldots, x_n)),i_{p^{\prime},\alpha }(y) \rangle _{p,p^{\prime}} - \langle M_{\widetilde{\phi }}( i_{p_1,\alpha }(x_1),\ldots, i_{p_n,\alpha }(x_n) ), i_{p^{\prime},\alpha }(y) \rangle \vert \\ &\quad= \bigg \vert \frac{1}{\mu (F_\alpha )} \int _{K^{\times n}} \int _{G} \Phi (k_1\ldots k_n t_n, \ldots, k_n t_n, t_n) \Psi _\alpha (k_1\ldots k_nt_n,\ldots, k_nt_n, t_n) \times \\ & \qquad \Delta (k_2 \dots k_n t_n) \dots \Delta (k_nt_n) \Delta (t_n) dt_n dk_1 \ldots dk_n \bigg \vert \\ &\quad\leq \frac{M}{\mu (F_\alpha )} \int _{K^{\times n}} \int _G \Psi _\alpha (k_1\ldots k_nt_n,\ldots, k_nt_n, t_n) dt_n dk_1 \ldots dk_n \\ &\quad= \frac{M}{\mu (F_\alpha )} \int _{K^{\times n}} \mu \left (F_\alpha \cap (k_1\ldots k_n)^{-1}F_\alpha \setminus \left ( (k_2\ldots k_n)^{-1}F_\alpha \cap \ldots \cap k_n^{-1}F_\alpha \right )\right ) dk_1 \ldots dk_n\\ &\quad\leq \frac{M}{\mu (F_\alpha )} \int _{K^{\times n}} \sum _{i=2}^n \mu (F_\alpha \setminus (k_i \ldots k_n)^{-1}F_\alpha ) dk_1 \ldots dk_n\\ & \quad\leq M (n-1) \mu (K)^n \sup _{k \in K^{1-n}} \frac{\mu (F_{\alpha } \setminus kF_{\alpha })}{\mu (F_\alpha )}. \end{split} \end{equation}
Using the ordering described earlier, if the index
![]() $\alpha \geq (\varepsilon \times \left (Mn \mu _G(K)^n\right )^{-1}, K^{1-n})$
, then the Følner condition implies that (5.6) is less than
$\alpha \geq (\varepsilon \times \left (Mn \mu _G(K)^n\right )^{-1}, K^{1-n})$
, then the Følner condition implies that (5.6) is less than
![]() $\varepsilon$
, and hence the limit (5.1) holds.
$\varepsilon$
, and hence the limit (5.1) holds.
From (5.1), it follows from writing out the definitions that the matrix amplifications of
![]() $i_{p,\alpha }$
also approximately intertwine the multiplicative amplifications of the Fourier and Schur multipliers; that is, for
$i_{p,\alpha }$
also approximately intertwine the multiplicative amplifications of the Fourier and Schur multipliers; that is, for
![]() $\beta _i \in S_{p_i}^N, \beta \in S_{p^{\prime}}^{N}$
, we have
$\beta _i \in S_{p_i}^N, \beta \in S_{p^{\prime}}^{N}$
, we have
 \begin{equation} \begin{split} &\Big |\langle{\mathrm{id}} \otimes i_{p,\alpha }(T^{(N)}_\phi (\beta _1\otimes x_1,\ldots, \beta _n \otimes x_n)),{\mathrm{id}}\otimes i_{p^{\prime},\alpha }(\beta \otimes y) \rangle _{p,p^{\prime}} \\ &\quad - \langle M^{(N)}_{\widetilde{\phi }}({\mathrm{id}}\otimes i_{p_1,\alpha }(\beta _1 \otimes x_1),\ldots, {\mathrm{id}}\otimes i_{p_n,\alpha }(\beta _n \otimes x_n) ), {\mathrm{id}}\otimes i_{p^{\prime},\alpha }(\beta \otimes y) \rangle \Big | \to 0 \end{split} \end{equation}
\begin{equation} \begin{split} &\Big |\langle{\mathrm{id}} \otimes i_{p,\alpha }(T^{(N)}_\phi (\beta _1\otimes x_1,\ldots, \beta _n \otimes x_n)),{\mathrm{id}}\otimes i_{p^{\prime},\alpha }(\beta \otimes y) \rangle _{p,p^{\prime}} \\ &\quad - \langle M^{(N)}_{\widetilde{\phi }}({\mathrm{id}}\otimes i_{p_1,\alpha }(\beta _1 \otimes x_1),\ldots, {\mathrm{id}}\otimes i_{p_n,\alpha }(\beta _n \otimes x_n) ), {\mathrm{id}}\otimes i_{p^{\prime},\alpha }(\beta \otimes y) \rangle \Big | \to 0 \end{split} \end{equation}
Corollary 5.2.
Let
![]() $G$
be an amenable locally compact group and
$G$
be an amenable locally compact group and
![]() $1 \leq p, p_1, \dots, p_n \leq \infty$
be such that
$1 \leq p, p_1, \dots, p_n \leq \infty$
be such that
![]() $\frac 1p=\sum _{i=1}^n \frac 1{p_i}$
. Let
$\frac 1p=\sum _{i=1}^n \frac 1{p_i}$
. Let
![]() $\phi \in L_\infty (G^{\times n})$
. If
$\phi \in L_\infty (G^{\times n})$
. If
![]() $\widetilde{\phi }$
is the symbol of a
$\widetilde{\phi }$
is the symbol of a
![]() $(p_1, \dots, p_n)$
-bounded (resp. multiplicatively bounded) Schur multiplier then
$(p_1, \dots, p_n)$
-bounded (resp. multiplicatively bounded) Schur multiplier then
![]() $\phi$
is the symbol of a
$\phi$
is the symbol of a
![]() $(p_1, \dots, p_n)$
-bounded (resp. multiplicatively bounded) Fourier multiplier. Moreover,
$(p_1, \dots, p_n)$
-bounded (resp. multiplicatively bounded) Fourier multiplier. Moreover,
Proof. Let
![]() $x_i$
be as in the hypotheses of Theorem5.1, and let
$x_i$
be as in the hypotheses of Theorem5.1, and let
![]() $i_{p,\alpha }$
be as in the proof of Theorem5.1. Let
$i_{p,\alpha }$
be as in the proof of Theorem5.1. Let
![]() $p^{\prime}$
be the Holder conjugate of
$p^{\prime}$
be the Holder conjugate of
![]() $p$
. In [Reference Caspers and de la Salle3, Theorem 5.2], it is proven that
$p$
. In [Reference Caspers and de la Salle3, Theorem 5.2], it is proven that
Note that this inequality also holds and in fact is explicitly proven for
![]() $p = \infty$
; by symmetry, it also holds for
$p = \infty$
; by symmetry, it also holds for
![]() $p=1$
. We remark that this result also uses the Følner condition.
$p=1$
. We remark that this result also uses the Følner condition.
Let
![]() $\varepsilon \gt 0$
. Then we can find
$\varepsilon \gt 0$
. Then we can find
![]() $y = \Delta ^{a} \lambda (f) \Delta ^b$
,
$y = \Delta ^{a} \lambda (f) \Delta ^b$
,
![]() $f \in C_c(G) \star C_c(G)$
such that
$f \in C_c(G) \star C_c(G)$
such that
![]() $\|y\|_{L_{p^{\prime}}(\mathcal{L} G)} \leq 1$
and
$\|y\|_{L_{p^{\prime}}(\mathcal{L} G)} \leq 1$
and
Next, by (5.8) and Theorem5.1, we can find
![]() $\alpha \in I$
such that the following two inequalities hold:
$\alpha \in I$
such that the following two inequalities hold:
and
By combining these inequalities, we find
 \begin{align*} \begin{split} \|T_{\phi }(x_1, \dots, x_n)\|_{L_p(\mathcal{L} G)} &\leq |\langle M_{\widetilde{\phi }}( i_{p_1,\alpha }(x_1),\ldots, i_{p_n,\alpha }(x_n) ), i_{p^{\prime},\alpha }(y) \rangle _{p,p^{\prime}}| + 3\varepsilon \\ &\leq \|M_{\widetilde{\phi }}\|_{(p_1, \dots, p_n)} \prod _{i=1}^n \|x_i\|_{L_{p_i}(\mathcal{L} G)} + 3\varepsilon \end{split} \end{align*}
\begin{align*} \begin{split} \|T_{\phi }(x_1, \dots, x_n)\|_{L_p(\mathcal{L} G)} &\leq |\langle M_{\widetilde{\phi }}( i_{p_1,\alpha }(x_1),\ldots, i_{p_n,\alpha }(x_n) ), i_{p^{\prime},\alpha }(y) \rangle _{p,p^{\prime}}| + 3\varepsilon \\ &\leq \|M_{\widetilde{\phi }}\|_{(p_1, \dots, p_n)} \prod _{i=1}^n \|x_i\|_{L_{p_i}(\mathcal{L} G)} + 3\varepsilon \end{split} \end{align*}
The elements
![]() $x_i$
as chosen above are norm dense in
$x_i$
as chosen above are norm dense in
![]() $L_{p_i}(\mathcal{L} G)$
(resp.
$L_{p_i}(\mathcal{L} G)$
(resp.
![]() $C^*_\lambda (G)$
when
$C^*_\lambda (G)$
when
![]() $p_i = \infty$
); hence, we get the required bound. The multiplicative bound follows similarly.
$p_i = \infty$
); hence, we get the required bound. The multiplicative bound follows similarly.
Remark 5.3. In [Reference Caspers and de la Salle3], [Reference Caspers, Krishnaswamy-Usha and Vos6], the proof runs via an ultraproduct construction. The ultraproduct is not actually necessary as demonstrated above, as all limits are usual limits and not ultralimits.
We can now extend the result of [Reference Caspers, Krishnaswamy-Usha and Vos6, Corollary 4.3] to non-unimodular groups. It is also a multiplicatively bounded, non-unimodular version of [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi5, Theorem 4.5]. Moreover, we no longer need the SAIN condition, and the subgroup no longer needs to be discrete.
Corollary 5.4.
Let
![]() $G$
be a locally compact, first countable group, and let
$G$
be a locally compact, first countable group, and let
![]() $1 \leq p \leq \infty$
and
$1 \leq p \leq \infty$
and
![]() $1 \lt p_1, \dots, p_n \leq \infty$
with
$1 \lt p_1, \dots, p_n \leq \infty$
with
![]() $p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
$p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
![]() $\phi \in C_b(G^{\times n})$
, which defines a
$\phi \in C_b(G^{\times n})$
, which defines a
![]() $(p_1, \dots, p_n)$
-mb Fourier multiplier, and let
$(p_1, \dots, p_n)$
-mb Fourier multiplier, and let
![]() $H \leq G$
be an amenable subgroup. Then
$H \leq G$
be an amenable subgroup. Then
Proof. The associated inequality for Schur multipliers follows from Theorem2.2. Now Corollary 5.2 (using amenability of
![]() $H$
) and Theorem4.1 yield the result.
$H$
) and Theorem4.1 yield the result.
In the next corollary, we prove a necessary condition for a ‘Fourier multiplier’ to satisfy (5.1) for the embeddings
![]() $i_{p,\alpha }$
defined above. This was used in the discussion in Section 3.
$i_{p,\alpha }$
defined above. This was used in the discussion in Section 3.
Corollary 5.5.
Fix
![]() $n \gt 1$
,
$n \gt 1$
,
![]() $1 \leq p_1, \dots, p_n, p, p^{\prime} \leq \infty$
such that
$1 \leq p_1, \dots, p_n, p, p^{\prime} \leq \infty$
such that
![]() $\frac 1p = \sum _{i=1}^n \frac 1{p_i} = 1 - \frac 1{p^{\prime}}$
, and let
$\frac 1p = \sum _{i=1}^n \frac 1{p_i} = 1 - \frac 1{p^{\prime}}$
, and let
![]() $\theta _1, \dots, \theta _n, \theta, \theta ^{\prime} \in [0,1]$
. Let
$\theta _1, \dots, \theta _n, \theta, \theta ^{\prime} \in [0,1]$
. Let
![]() $i_{p,\alpha }$
be as in the proof of Theorem
5.1
. Assume that for each
$i_{p,\alpha }$
be as in the proof of Theorem
5.1
. Assume that for each
![]() $\phi \in L_\infty (G^{\times n})$
, we have a map
$\phi \in L_\infty (G^{\times n})$
, we have a map
![]() $S_\phi \,:\,{\kappa }^{\theta _1}_{p_i}(L) \times \ldots \times{\kappa }^{\theta _n}_{p_n}(L) \to{\kappa }^{\theta }_p(L)$
satisfying
$S_\phi \,:\,{\kappa }^{\theta _1}_{p_i}(L) \times \ldots \times{\kappa }^{\theta _n}_{p_n}(L) \to{\kappa }^{\theta }_p(L)$
satisfying
for
![]() $x_i \in{\kappa }_{p_i}^{\theta _i}(L)$
,
$x_i \in{\kappa }_{p_i}^{\theta _i}(L)$
,
![]() $y \in{\kappa }_{p^{\prime}}^{\theta ^{\prime}}(L)$
. Now let
$y \in{\kappa }_{p^{\prime}}^{\theta ^{\prime}}(L)$
. Now let
![]() $\phi (s_1, \dots, s_n) = \phi _1(s_1)\ldots \phi _n(s_n)$
for some functions
$\phi (s_1, \dots, s_n) = \phi _1(s_1)\ldots \phi _n(s_n)$
for some functions
![]() $\phi _1, \dots, \phi _n \in L^\infty (G)$
. Then
$\phi _1, \dots, \phi _n \in L^\infty (G)$
. Then
![]() $S_\phi$
must satisfy
$S_\phi$
must satisfy
for
![]() $x_i \in{\kappa }^{\theta _i}_{p_i}(L)$
,
$x_i \in{\kappa }^{\theta _i}_{p_i}(L)$
,
![]() $i = 1, \dots, n$
.
$i = 1, \dots, n$
.
Proof. Fix some
![]() $y \in{\kappa }^{\theta ^{\prime}}_{p^{\prime}}(L)$
. By density, it suffices to show that
$y \in{\kappa }^{\theta ^{\prime}}_{p^{\prime}}(L)$
. By density, it suffices to show that
By (5.8), it suffices to show
By running the proof of Theorem5.1 with the constant 1 function in place of
![]() $\phi$
and
$\phi$
and
![]() $T_{\phi _i}(x_i)$
in place of
$T_{\phi _i}(x_i)$
in place of
![]() $x_i$
, we find that
$x_i$
, we find that
Since multiplication with
![]() $\phi _i$
only maps
$\phi _i$
only maps
![]() $C_c(G) \star C_c(G)$
to
$C_c(G) \star C_c(G)$
to
![]() $C_c(G)$
, we no longer need to have that
$C_c(G)$
, we no longer need to have that
![]() $T_{\phi _i}(x_i) \in{\kappa }_{p_i}^{\theta _i}(L)$
, so we cannot apply Theorem5.1 directly. But since we have
$T_{\phi _i}(x_i) \in{\kappa }_{p_i}^{\theta _i}(L)$
, so we cannot apply Theorem5.1 directly. But since we have
![]() $\phi = 1$
, this does not give any technical complications in the proof.
$\phi = 1$
, this does not give any technical complications in the proof.
Using the kernel representations, it is straightforward to show that
By combining the above observations with (5.9), we get the required result.
6. Linear intertwining result
In this section, we sketch the proof of Proposition 4.3. The main ingredient to be added to already existing results is the extension of [Reference Conde-Alonso, Parcet and Ricard9, Lemma 3.1] to general von Neumann algebras via Haagerup reduction. The Haagerup reduction method is described by Theorem6.1, proved for
![]() $\sigma$
-finite von Neumann algebras in [Reference Haagerup, Junge and Xu12] and extended to the weight case in [Reference Caspers, Parcet, Perrin and Ricard8, Section 8]. We will assume that the reader is familiar with Tomita–Takesaki theory, conditional expectations and such. We refer to [Reference Takesaki24] for the background.
$\sigma$
-finite von Neumann algebras in [Reference Haagerup, Junge and Xu12] and extended to the weight case in [Reference Caspers, Parcet, Perrin and Ricard8, Section 8]. We will assume that the reader is familiar with Tomita–Takesaki theory, conditional expectations and such. We refer to [Reference Takesaki24] for the background.
Denote by
![]() $\sigma ^\varphi$
the modular automorphism group of a normal faithful semifinite (nfs) weight
$\sigma ^\varphi$
the modular automorphism group of a normal faithful semifinite (nfs) weight
![]() $\varphi$
. Recall that the centraliser
$\varphi$
. Recall that the centraliser
![]() $\mathcal{N}_\varphi$
of a nfs weight
$\mathcal{N}_\varphi$
of a nfs weight
![]() $\varphi$
on a von Neumann algebra
$\varphi$
on a von Neumann algebra
![]() $\mathcal{M}$
is given by
$\mathcal{M}$
is given by
Theorem 6.1.
Let
![]() $(\mathcal{M}, \varphi )$
be any von Neumann algebra equipped with a nfs weight. There is another von Neumann algebra
$(\mathcal{M}, \varphi )$
be any von Neumann algebra equipped with a nfs weight. There is another von Neumann algebra
![]() $({\mathcal{R}}, \widehat{\varphi })$
containing
$({\mathcal{R}}, \widehat{\varphi })$
containing
![]() $\mathcal{M}$
and with nfs weight
$\mathcal{M}$
and with nfs weight
![]() $\widehat{\varphi }$
extending
$\widehat{\varphi }$
extending
![]() $\varphi$
and elements
$\varphi$
and elements
![]() $a_n$
in the center of the centraliser of
$a_n$
in the center of the centraliser of
![]() $\widehat{\varphi }$
such that the following properties hold:
$\widehat{\varphi }$
such that the following properties hold:
-
1. There is a conditional expectation
 ${\mathcal{E}}\,:\,{\mathcal{R}} \to \mathcal{M}$
satisfying
${\mathcal{E}}\,:\,{\mathcal{R}} \to \mathcal{M}$
satisfying
 \begin{equation*} \varphi \circ {\mathcal {E}} = \widehat {\varphi }, \qquad \sigma _s^{\varphi } \circ {\mathcal {E}} = {\mathcal {E}} \circ \sigma _s^{\widehat {\varphi }}, \quad s \in {\mathrm {\mathbb {R}}}.\end{equation*}
\begin{equation*} \varphi \circ {\mathcal {E}} = \widehat {\varphi }, \qquad \sigma _s^{\varphi } \circ {\mathcal {E}} = {\mathcal {E}} \circ \sigma _s^{\widehat {\varphi }}, \quad s \in {\mathrm {\mathbb {R}}}.\end{equation*}
-
2. The centralisers
 ${\mathcal{R}}_n$
of the weights
${\mathcal{R}}_n$
of the weights
 $\varphi _n \,:\!=\, \varphi (e^{-a_n}{\cdot} )$
are semifinite for
$\varphi _n \,:\!=\, \varphi (e^{-a_n}{\cdot} )$
are semifinite for
 $n \geq 1$
.
$n \geq 1$
. -
3. There are conditional expectations
 ${\mathcal{E}}_n\,:\,{\mathcal{R}} \to{\mathcal{R}}_n$
satisfying
${\mathcal{E}}_n\,:\,{\mathcal{R}} \to{\mathcal{R}}_n$
satisfying
 \begin{equation*} \widehat {\varphi } \circ {\mathcal {E}}_n = \widehat {\varphi }, \qquad \sigma _s^{\widehat {\varphi }} \circ {\mathcal {E}}_n = {\mathcal {E}}_n \circ \sigma _s^{\widehat {\varphi }}, \quad s \in {\mathrm {\mathbb {R}}}\end{equation*}
\begin{equation*} \widehat {\varphi } \circ {\mathcal {E}}_n = \widehat {\varphi }, \qquad \sigma _s^{\widehat {\varphi }} \circ {\mathcal {E}}_n = {\mathcal {E}}_n \circ \sigma _s^{\widehat {\varphi }}, \quad s \in {\mathrm {\mathbb {R}}}\end{equation*}
-
4.
 ${\mathcal{E}}_n(x) \to x$
${\mathcal{E}}_n(x) \to x$
 $\sigma$
-strongly for
$\sigma$
-strongly for
 $x \in \mathfrak{n}_{\widehat \varphi }$
, and
$x \in \mathfrak{n}_{\widehat \varphi }$
, and
 $\bigcup _{n \geq 1}{\mathcal{R}}_n$
is
$\bigcup _{n \geq 1}{\mathcal{R}}_n$
is
 $\sigma$
-strongly dense in
$\sigma$
-strongly dense in
 $\mathcal{R}$
.
$\mathcal{R}$
.
We denote by
![]() $D_\varphi$
the spatial derivative with respect to
$D_\varphi$
the spatial derivative with respect to
![]() $\varphi$
(and some weight on the commutant, whose choice is unimportant). Assume that
$\varphi$
(and some weight on the commutant, whose choice is unimportant). Assume that
![]() $T\,:\, \mathcal{M} \to \mathcal{M}$
is unital completely positive (ucp) and satisfies
$T\,:\, \mathcal{M} \to \mathcal{M}$
is unital completely positive (ucp) and satisfies
![]() $\varphi \circ T \leq \varphi$
. Then by [Reference Haagerup, Junge and Xu12, Section 5],
$\varphi \circ T \leq \varphi$
. Then by [Reference Haagerup, Junge and Xu12, Section 5],
![]() $T$
‘extends’ to a map
$T$
‘extends’ to a map
![]() $T^{(p)}$
on
$T^{(p)}$
on
![]() $L_p(\mathcal{M})$
, in the sense that
$L_p(\mathcal{M})$
, in the sense that
![]() $T^{(p)}(D_\varphi ^{1/2p} x D_\varphi ^{1/2p}) = D_\varphi ^{1/2p} T(x) D_\varphi ^{1/2p}$
for
$T^{(p)}(D_\varphi ^{1/2p} x D_\varphi ^{1/2p}) = D_\varphi ^{1/2p} T(x) D_\varphi ^{1/2p}$
for
![]() $x \in{\mathfrak{m}}_{\widehat \varphi }$
. If
$x \in{\mathfrak{m}}_{\widehat \varphi }$
. If
![]() $T$
satisfies
$T$
satisfies
![]() $\sigma _s^\varphi \circ T = T \circ \sigma _s^\varphi$
, then we moreover have
$\sigma _s^\varphi \circ T = T \circ \sigma _s^\varphi$
, then we moreover have
![]() $T^{(p)}(D_\varphi ^{\theta /p} x D_\varphi ^{(1-\theta )/p}) = D_\varphi ^{\theta /p} T(x) D_\varphi ^{(1-\theta )/p}$
for any
$T^{(p)}(D_\varphi ^{\theta /p} x D_\varphi ^{(1-\theta )/p}) = D_\varphi ^{\theta /p} T(x) D_\varphi ^{(1-\theta )/p}$
for any
![]() $0 \leq \theta \leq 1$
and
$0 \leq \theta \leq 1$
and
![]() $x \in{\mathfrak{m}}_{\widehat \varphi }$
.
$x \in{\mathfrak{m}}_{\widehat \varphi }$
.
In particular, the conditional expectations
![]() ${\mathcal{E}},{\mathcal{E}}_n$
‘extend’ to maps
${\mathcal{E}},{\mathcal{E}}_n$
‘extend’ to maps
![]() ${\mathcal{E}}^{(p)},{\mathcal{E}}_n^{(p)}$
from
${\mathcal{E}}^{(p)},{\mathcal{E}}_n^{(p)}$
from
![]() $L_p({\mathcal{R}}, \widehat{\varphi })$
to
$L_p({\mathcal{R}}, \widehat{\varphi })$
to
![]() $L_p(\mathcal{M}, \varphi )$
resp.
$L_p(\mathcal{M}, \varphi )$
resp.
![]() $L_p({\mathcal{R}}_n, \widehat{\varphi })$
. The following statement is [Reference Caspers, Parcet, Perrin and Ricard8, Lemma 8.3]:
$L_p({\mathcal{R}}_n, \widehat{\varphi })$
. The following statement is [Reference Caspers, Parcet, Perrin and Ricard8, Lemma 8.3]:
We need a few more facts; we refer to [Reference Caspers, Parcet, Perrin and Ricard8, Section 8.2] for the details. First, there is an isometric isomorphism
![]() ${\kappa }_p\,:\, L_p({\mathcal{R}}_n, \widehat{\varphi }) \to L_p({\mathcal{R}}_n, \varphi _n)$
given by
${\kappa }_p\,:\, L_p({\mathcal{R}}_n, \widehat{\varphi }) \to L_p({\mathcal{R}}_n, \varphi _n)$
given by
![]() ${\kappa }_p(D_{\widehat{\varphi }}^{1/2p}xD_{\widehat \varphi }^{1/2p}) = e^{a_n/2p} x e^{a_n/2p}$
for
${\kappa }_p(D_{\widehat{\varphi }}^{1/2p}xD_{\widehat \varphi }^{1/2p}) = e^{a_n/2p} x e^{a_n/2p}$
for
![]() $x \in{\mathfrak{m}}_{\widehat \varphi }$
. Next, assume that
$x \in{\mathfrak{m}}_{\widehat \varphi }$
. Next, assume that
![]() $T\,:\, \mathcal{M} \to \mathcal{M}$
is ucp and preserves
$T\,:\, \mathcal{M} \to \mathcal{M}$
is ucp and preserves
![]() $\varphi$
and
$\varphi$
and
![]() $\sigma _s^\varphi$
. Then by [Reference Haagerup, Junge and Xu12, Section 4], there exists an extension
$\sigma _s^\varphi$
. Then by [Reference Haagerup, Junge and Xu12, Section 4], there exists an extension
![]() $\widehat{T}\,:\,{\mathcal{R}} \to{\mathcal{R}}$
, which is also ucp and preserves
$\widehat{T}\,:\,{\mathcal{R}} \to{\mathcal{R}}$
, which is also ucp and preserves
![]() $\widehat{\varphi }$
and
$\widehat{\varphi }$
and
![]() $\sigma _s^{\widehat \varphi }$
. Hence
$\sigma _s^{\widehat \varphi }$
. Hence
![]() $\widehat{T}$
itself also ‘extends’ to the various noncommutative
$\widehat{T}$
itself also ‘extends’ to the various noncommutative
![]() $L_p$
-spaces. Moreover, the following diagram commutes:
$L_p$
-spaces. Moreover, the following diagram commutes:

Note that since
![]() $\varphi _n$
is tracial on
$\varphi _n$
is tracial on
![]() ${\mathcal{R}}_n$
, the
${\mathcal{R}}_n$
, the
![]() $\widehat{T}$
in the rightmost upwards arrow is actually an extension of the operator
$\widehat{T}$
in the rightmost upwards arrow is actually an extension of the operator
![]() $\widehat{T}$
on
$\widehat{T}$
on
![]() ${\mathcal{R}}_n$
, so we do not need to use the notation
${\mathcal{R}}_n$
, so we do not need to use the notation
![]() $\widehat{T}^{(p)}$
here.
$\widehat{T}^{(p)}$
here.
Finally, for
![]() $1 \leq p,q \lt \infty$
, we define the Mazur maps
$1 \leq p,q \lt \infty$
, we define the Mazur maps
![]() $M_{p,q}\,:\, L_p(\mathcal{M}) \to L_q(\mathcal{M})$
by
$M_{p,q}\,:\, L_p(\mathcal{M}) \to L_q(\mathcal{M})$
by
![]() $x \mapsto u |x|^{p/q}$
, where
$x \mapsto u |x|^{p/q}$
, where
![]() $x = u|x|$
is the polar decomposition of
$x = u|x|$
is the polar decomposition of
![]() $x$
. The Mazur maps satisfy
$x$
. The Mazur maps satisfy
![]() ${\kappa }_q \circ M_{p,q} = M_{p,q} \circ{\kappa }_p$
; see, for instance, [Reference Ricard23, end of Section 3]. We are now ready to state and prove the generalisation of [Reference Conde-Alonso, Parcet and Ricard9, Lemma 3.1] for general von Neumann algebras. This result was already shown for
${\kappa }_q \circ M_{p,q} = M_{p,q} \circ{\kappa }_p$
; see, for instance, [Reference Ricard23, end of Section 3]. We are now ready to state and prove the generalisation of [Reference Conde-Alonso, Parcet and Ricard9, Lemma 3.1] for general von Neumann algebras. This result was already shown for
![]() $2 \lt p \lt \infty$
in [Reference Caspers, Parcet, Perrin and Ricard8, Section 8], but we will prove the result for all
$2 \lt p \lt \infty$
in [Reference Caspers, Parcet, Perrin and Ricard8, Section 8], but we will prove the result for all
![]() $1 \lt p \lt \infty$
at once since this does not take any extra effort.
$1 \lt p \lt \infty$
at once since this does not take any extra effort.
Lemma 6.2.
Let
![]() $(\mathcal{M}, \varphi )$
be a von Neumann algebra equipped with nfs weight. Let
$(\mathcal{M}, \varphi )$
be a von Neumann algebra equipped with nfs weight. Let
![]() $T\,:\, \mathcal{M} \to \mathcal{M}$
be a unital completely positive map satisfying
$T\,:\, \mathcal{M} \to \mathcal{M}$
be a unital completely positive map satisfying
![]() $\varphi \circ T = \varphi$
and
$\varphi \circ T = \varphi$
and
![]() $T \circ \sigma _s^\varphi = \sigma _s^\varphi \circ T$
for all
$T \circ \sigma _s^\varphi = \sigma _s^\varphi \circ T$
for all
![]() $s \in{\mathrm{\mathbb{R}}}$
. Then there exists a universal constant
$s \in{\mathrm{\mathbb{R}}}$
. Then there exists a universal constant
![]() $C\gt 0$
such that for any
$C\gt 0$
such that for any
![]() $x \in L_2(\mathcal{M})$
and
$x \in L_2(\mathcal{M})$
and
![]() $1 \lt p \lt \infty$
:
$1 \lt p \lt \infty$
:
where
![]() $\theta = \frac 14 \min \{\frac p2, \frac 2p\}$
.
$\theta = \frac 14 \min \{\frac p2, \frac 2p\}$
.
Proof. The proof runs via Haagerup reduction, using the estimates for the semifinite case from [Reference Caspers, Parcet, Perrin and Ricard8, Claim B] for
![]() $p \gt 2$
and [Reference Conde-Alonso, Parcet and Ricard9, Lemma 3.1] for
$p \gt 2$
and [Reference Conde-Alonso, Parcet and Ricard9, Lemma 3.1] for
![]() $p \lt 2$
. Note that the latter was stated only for finite von Neumann algebras, but the same proof works for the semifinite case as well.
$p \lt 2$
. Note that the latter was stated only for finite von Neumann algebras, but the same proof works for the semifinite case as well.
Set
![]() $y = M_{2,p}(x)$
. Since
$y = M_{2,p}(x)$
. Since
![]() $T = \widehat{T}$
on
$T = \widehat{T}$
on
![]() $\mathcal{M}$
and
$\mathcal{M}$
and
![]() $L_p(\mathcal{M}, \varphi ) \hookrightarrow L_p({\mathcal{R}}, \widehat \varphi )$
canonically and isometrically, we have
$L_p(\mathcal{M}, \varphi ) \hookrightarrow L_p({\mathcal{R}}, \widehat \varphi )$
canonically and isometrically, we have
![]() $T^{(p)}(y) = \widehat{T}^{(p)}(y)$
and
$T^{(p)}(y) = \widehat{T}^{(p)}(y)$
and
Now fix
![]() $n \geq 1$
. Then
$n \geq 1$
. Then
Now we can apply the result for the semifinite case on
![]() ${\kappa }_p({\mathcal{E}}_n^{(p)}(y))$
to obtain
${\kappa }_p({\mathcal{E}}_n^{(p)}(y))$
to obtain
 \begin{align*} \begin{split} &\|{\mathcal{E}}_n^{(p)}(\widehat{T}^{(p)}(y)) -{\mathcal{E}}_n^{(p)}(y)\|_{L_p({\mathcal{R}}_n, \widehat \varphi )} \\ &\quad \leq \ C \|\hat{T}(M_{p,2}({\kappa }_p({\mathcal{E}}_n^{(p)}(y)))) - M_{p,2}({\kappa }_p({\mathcal{E}}_n^{(p)}(y)))\|_{L_2({\mathcal{R}}_n, \varphi _n)}^\theta \cdot \|M_{p,2}({\kappa }_p({\mathcal{E}}_n^{(p)}(y)))\|_{L_2({\mathcal{R}}_n, \varphi _n)}^{1-\theta } \\ &\quad= C \|{\kappa }_2(\hat{T}^{(2)}(M_{p,2}({\mathcal{E}}_n^{(p)}(y)))) -{\kappa }_2(M_{p,2}({\mathcal{E}}_n^{(p)}(y)))\|_{L_2({\mathcal{R}}_n, \varphi _n)}^\theta \cdot \|{\kappa }_2(M_{p,2}({\mathcal{E}}_n^{(p)}(y)))\|_{L_2({\mathcal{R}}_n, \varphi _n)}^{1-\theta } \\ &\quad= C \|\hat{T}^{(2)}(M_{p,2}({\mathcal{E}}_n^{(p)}(y))) - M_{p,2}({\mathcal{E}}_n^{(p)}(y))\|_{L_2({\mathcal{R}}_n, \widehat \varphi )}^\theta \cdot \|M_{p,2}({\mathcal{E}}_n^{(p)}(y))\|_{L_2({\mathcal{R}}_n, \widehat \varphi )}^{1-\theta } \\ &\quad\,=\!:\, C A_n^\theta B_n^{1-\theta }.\\ \end{split} \end{align*}
\begin{align*} \begin{split} &\|{\mathcal{E}}_n^{(p)}(\widehat{T}^{(p)}(y)) -{\mathcal{E}}_n^{(p)}(y)\|_{L_p({\mathcal{R}}_n, \widehat \varphi )} \\ &\quad \leq \ C \|\hat{T}(M_{p,2}({\kappa }_p({\mathcal{E}}_n^{(p)}(y)))) - M_{p,2}({\kappa }_p({\mathcal{E}}_n^{(p)}(y)))\|_{L_2({\mathcal{R}}_n, \varphi _n)}^\theta \cdot \|M_{p,2}({\kappa }_p({\mathcal{E}}_n^{(p)}(y)))\|_{L_2({\mathcal{R}}_n, \varphi _n)}^{1-\theta } \\ &\quad= C \|{\kappa }_2(\hat{T}^{(2)}(M_{p,2}({\mathcal{E}}_n^{(p)}(y)))) -{\kappa }_2(M_{p,2}({\mathcal{E}}_n^{(p)}(y)))\|_{L_2({\mathcal{R}}_n, \varphi _n)}^\theta \cdot \|{\kappa }_2(M_{p,2}({\mathcal{E}}_n^{(p)}(y)))\|_{L_2({\mathcal{R}}_n, \varphi _n)}^{1-\theta } \\ &\quad= C \|\hat{T}^{(2)}(M_{p,2}({\mathcal{E}}_n^{(p)}(y))) - M_{p,2}({\mathcal{E}}_n^{(p)}(y))\|_{L_2({\mathcal{R}}_n, \widehat \varphi )}^\theta \cdot \|M_{p,2}({\mathcal{E}}_n^{(p)}(y))\|_{L_2({\mathcal{R}}_n, \widehat \varphi )}^{1-\theta } \\ &\quad\,=\!:\, C A_n^\theta B_n^{1-\theta }.\\ \end{split} \end{align*}
By the triangle inequality, the main result from [Reference Ricard23] and (6.1), we find
 \begin{align*} \begin{split} B_n &\leq \|M_{p,2}({\mathcal{E}}_n^{(p)}(y)) - M_{p,2}(y)\|_{L_2({\mathcal{R}}_n, \widehat \varphi )} + \|M_{p,2}(y)\|_{L_2({\mathcal{R}}_n, \widehat \varphi )} \\ &\leq C_{x,p} \|{\mathcal{E}}_n^{(p)}(y) - y\|_{L_p({\mathcal{R}}_n, \widehat \varphi )}^{\min \{\frac p2, 1\}} + \|x\|_{L_2({\mathcal{R}}_n, \widehat \varphi )} \to \|x\|_{L_2(\mathcal{M}, \varphi )} \end{split} \end{align*}
\begin{align*} \begin{split} B_n &\leq \|M_{p,2}({\mathcal{E}}_n^{(p)}(y)) - M_{p,2}(y)\|_{L_2({\mathcal{R}}_n, \widehat \varphi )} + \|M_{p,2}(y)\|_{L_2({\mathcal{R}}_n, \widehat \varphi )} \\ &\leq C_{x,p} \|{\mathcal{E}}_n^{(p)}(y) - y\|_{L_p({\mathcal{R}}_n, \widehat \varphi )}^{\min \{\frac p2, 1\}} + \|x\|_{L_2({\mathcal{R}}_n, \widehat \varphi )} \to \|x\|_{L_2(\mathcal{M}, \varphi )} \end{split} \end{align*}
for some constant
![]() $C_{x,p}$
independent of
$C_{x,p}$
independent of
![]() $n$
. Similarly, we find
$n$
. Similarly, we find
Hence, taking limits and applying again (6.1), we conclude
Proof of Proposition 4.3. We indicate only the changes to [Reference Caspers, Parcet, Perrin and Ricard8, Proof of Claim B]. The statement we have to prove is precisely [Reference Caspers, Parcet, Perrin and Ricard8, Equation (9)], but without the
![]() $u_j$
(this is just a different choice based on convenience). The
$u_j$
(this is just a different choice based on convenience). The
![]() $T_\zeta$
constructed in [Reference Caspers, Parcet, Perrin and Ricard8, Proof of Claim B] is a
$T_\zeta$
constructed in [Reference Caspers, Parcet, Perrin and Ricard8, Proof of Claim B] is a
![]() $\varphi$
-preserving ucp map that commutes with the modular automorphism group; one can see this from (2.4). Hence, we can apply Lemma 6.2 on
$\varphi$
-preserving ucp map that commutes with the modular automorphism group; one can see this from (2.4). Hence, we can apply Lemma 6.2 on
![]() $T_\zeta$
and
$T_\zeta$
and
![]() $h_V$
to show [Reference Caspers, Parcet, Perrin and Ricard8, Equation (10)] (but without the
$h_V$
to show [Reference Caspers, Parcet, Perrin and Ricard8, Equation (10)] (but without the
![]() $u_j$
). Then, setting
$u_j$
). Then, setting
![]() $z_j = h_V^{2/q}$
, the rest of the proof is the same.
$z_j = h_V^{2/q}$
, the rest of the proof is the same.
Acknowledgement
The author thanks Martijn Caspers for useful discussions and a thorough proofreading of the manuscript.
Competing interests
The author declares none.
Funding statement
GV is supported by the NWO Vidi grant VI.Vidi.192.018 ‘Non-commutative harmonic analysis and rigidity of operator algebras’.