Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-30T03:08:57.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Trace rings of generic matrices are unique factorization domains

Published online by Cambridge University Press:  18 May 2009

Lieven Le Bruyn
Lieven Le Bruyn
Affiliation:
Department of Mathematics, University of Antwerp, UIA Universiteitsplein 1, 2610 Wilrijk, Belgium
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A. W. Chatters and D. A. Jordan defined in [0] a unique factorization ring to be a prime ring in which every height one prime ideal is principal. In this note we will prove that the trace ring of m generic n × n-matrices satisfies this condition.

Throughout this note, k will be a field of characteristic zero. Consider the polynomial ring S = k[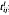;1≤i, j≤n, 1≤l≤m] and the n × n matrices Xl = 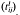in Mn(S). The k-subalgebra of Mn(S) generated by {Xl; 1≤l≤m} is called the ring of m generic n × n matrices Gm,n. Adjoining to it the traces of all its elements we obtain the trace ring 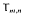of m n × n generic matrices, cfr. e.g. [1].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 28 , Issue 1 , January 1986 , pp. 11 - 13
Copyright
Copyright © Glasgow Mathematical Journal Trust 1986

References

REFERENCES

0.Chatters, A. W. and Jordan, D. A., Non-commutative unique factorization rings, preprint.Google Scholar
1.Amitsur, S. A. and Small, Lance W., Prime Ideals in p.i. Rings, J. Algebra 62 (1980), 358–383.CrossRefGoogle Scholar
2.Artin, Emil, Letter dated 12 3rd, 1982.Google Scholar
3.Auslander, Maurice and Goldman, Oscar, Maximal Orders, Trans. Amer. Math. Soc. 97 (1960), 1–24.CrossRefGoogle Scholar
4.Fossum, Robert M., The Divisor Class Group of a Krull Domain, Ergebn. der Math. Wiss. 74 (Springer Verlag, 1973).CrossRefGoogle Scholar
5.Bruyn, Lieven Le, Homological Properties of Trace Rings of Generic Matrices, Trans. Amer. Math. Soc. (to appear).Google Scholar
6.Procesi, Claudio, Invariant Theory of n × n Matrices, Advances in Math. (1976).CrossRefGoogle Scholar
7.Small, Lance W. and Stafford, J. T., Holological Properties of Generic Matrices, Israel J. Math., (to appear).Google Scholar
8.Yuan, Shuen, Reflexive Modules and Algebra Class Groups over Noetherian Integrally Closed Domains, J. Algebra 32 (1974), 405–417.CrossRefGoogle Scholar